Вероятностные формальные понятия в некоторых задачах классификации

Анализ формальных понятий (АФП) [1] содержит в себе удобный инструментарий для представления и обработки различных данных. Формальные понятия образуют целостные объединения групп свойств и объектов и поэтому являются очевидными кандидатами на классификационные единицы. Это позволяет использовать их при решении задач кластеризации и классификации.

В рамках АФП изучается весь спектр задач анализа данных. За последние годы опубликованы работы по извлечению паттернов атрибутов [2, 3], работы по алгоритмам кластеризации и извлечению ассоциативных правил, предпринят ряд попыток построения алгоритмов классификации и др. [4-7]. Для нас особый интерес представляет работа [7], где предложен алгоритм построения решающих деревьев на основе решетки формальных понятий, а результаты экспериментов представлены в виде таблицы с измерениями точности работы алгоритмов. Это позволяет сравнить точность предлагаемых алгоритмов классификации, разработанных на основе вероятностных формальных понятий и соответствующего алгоритма кластеризации с результатами этих алгоритмов.

Раздел 1 предлагаемой статьи посвящен определению вероятностных и статистических формальных понятий. В разделе 2 приводятся основные алгоритмы их построения: Prob-

Closure для вероятностных, StatClosure для статистических формальных понятий. Центральным можно считать раздел 3, где рассматриваются основные практические модификации процедуры StatClosure - алгоритмы ClassifyInCluster , ClassifyOverClusters , - а также различные параметризации этих алгоритмов, позволяющие придать предлагаемому подходу требуемую гибкость. В разделе 4 приводятся результаты классификации, полученные этими алгоритмами. Протоколы экспериментов и сравнение с близкими по семантике методами классификации даются в разделе 5. В качестве опорных рассматриваются результаты, полученные в [7] с помощью построения решающих деревьев на основе решетки формальных понятий, что позволяет более наглядно показать эффективность методов ClassifyInCluster и ClassifyOverClusters .

1    Вероятностные и статистические формальные понятия

Напомним базовые определения АФП [1].

Определение 1 . Формальный контекст - K = ( G , M , I ) , где G - множество объектов, M - множество атрибутов и I с G х M - отношение принадлежности атрибутов объектам.

Определение 2 . A с G , B с M . Тогда:

• •   A ^ = { m е M | V g е A, ( g , m ) е I } ;

• •   B ^г = { g е G | V m е B,(g , m ) е I } ;

• •   ( A, B ) - формальное понятие, если A ^f = B и B ^ = A .

Определение 3 . R = ( B , C ) - импликация, R еК = Imp( K ), если B ^ с C ^ и B , C с M .

При этом B = R ^ называется посылкой, а C = R ^ - заключением импликации. Оператор логического вывода, использующий множество импликаций ℜ , добавляет к некоторому множеству атрибутов L другие, выводимые из него атрибуты:

П_К ( L ) = L о { C | 3 R еК : R* с L , R ^ = C }.

Вероятностное обобщение формальных понятий можно получить [8], опираясь на следующий результат.

Теорема 1 [1]. Множество неподвижных точек оператора логического вывода совпадает с множеством формальных понятий. Для любого множества B с M , П^ (B) = B ^ B^w = B .

Вероятностные формальные понятия мы получим как неподвижные точки соответсвующего вероятностного оператора логического вывода. Для его определения построим логико-вероятностную модель, описывающую формальный контекст K .

Определение 4 . Для конечного контекста K = ( G , M , I ) определим сигнатуру контекста ст _к , содержащую лишь множество предикатных символов, совпадающее с M . Для сигнатуры <т_к и контекста K как модели определим интерпретацию предикатных символов следующим образом: K 1= m ( x ) ^ ( x , m ) е I .

Определение 5 . Определим классические логические конструкции:

• 1)    Term( K ) - множество термов состоит из символов переменных;

• 2)    At( K ) - атомами являются выражения m ( t ) , где m е ст _к и t е Term(K ) ;

• 3)    Lit ( K ) - литеры включают все атомы m ( t ) и их отрицания — m ( t ) ;

• 4)    For( K ) - определяется индуктивно: всякий атом - формула, и для любых Ф , Т е For( K ) синтаксические конструкции Ф л Т , Ф v Т , Ф ^ Т , —Ф - тоже формулы.

Определение 6 . Рассмотрим произвольную вероятностную меру ц на множестве G , определенную в колмогоровском смысле. Определим контекстную вероятностную меру на множестве формул как:

• ^{v :} For( K ) ^ [0,1], ^ ^{ф )} = ц ^({ g е G | g 1= ^{ф })}.

Определим правила на контексте, как аналог импликаций, а также их составные части.

• 1)    Правило R = ( H 1 , H ₂..., H k ^ C ) есть импликация ( H 1 л H ₂... л H k ^ с );

• 2)    Посылкой R " правила R называется набор литер { H 1 , H ₂..., H_k };

• 3)    Заключением правила является R ^ = C ;

• 4)    Длиной правила назовём мощность его посылки | R "  |;

• 5)    Если R " = R 2" и R ^ = R ^ , то R 1 = R ₂ .

Определение 8 . Вероятностью правила R является значение

П(R ) = v ( R ^ | R " ) = ^{V (} R ^Л R ) .

v ( R " )

Если знаменатель v ( R " ) равен 0, то вероятность правила неопределена.

Определение 9 . Правило R назовем максимально специфичным R е MSR( K ) , если нет правила R с более длинной посылкой R " с R " и более высокой вероятностью ~

П ^{( R} ) >  П ^{( R} ) .

Правила определения 7 позволяют установить вероятностный оператор замыкания. Для этого заменим множество импликаций Imp ( K ) на множество максимально специфических вероятностных правил. Поэтому ниже будем предполагать, что ” - множество максимально специфичных правил. По аналогии с теоремой 1 определим вероятностные формальные понятия как неподвижные точки оператора логического вывода, использующего множество правил ”.

Определение 10 . Замыканием L множества литер L будем называть наименьшую неподвижную точку оператора логического вывода, содержащую L :

L = П ” ( L ) = П ” ( L ) = U п ” ( L ).

k ∈ N

Определение 11 . Пусть ” с MSR( K ) - множество максимально специфических правил. Тогда B - вероятностное формальное понятие, если П ” ( B ) = B .

Теорема 2 [9]. Пусть ” - множество максимально специфических правил, тогда: если L непротиворечиво, то П ” ( L ) также непротиворечиво.

На основе определения 11 и теоремы 2 нетрудно предложить алгоритм замыкания ProbClosure, который для заданного множества литер B строит замыкание B , являющееся минимальной неподвижной точкой, содержащей множество B , и, в силу определения 11, вероятностным формальным понятием. Алгоритм ProbClosure не требует разрешения противоречий, так как в силу теоремы 2 исключается ситуация, когда в процессе вывода обнаруживается одновременно литера и ее отрицание.

Алгоритм 1. ProbClosure . Замыкание набора литер оператором вывода.

Вход: ” с For( K ) , K = ( G , M , I ) , B с Lit( K )

Выход: C с Lit( K ) - вероятностное формальное понятие

1:    Функция ProbClosure (K,^,B) 2:       Bo — В 3:       k — 0 4:       Повторять 5:                  Bk+1 - П.(Bk) 6:                k -— k +1 7:        До тех пор пока Bk Ф Bk 1 8:        Вернуть Bk 9:    Конец функции

В практических задачах контекст полностью неизвестен, а известна только некоторая выборка из контекста. Адекватной моделью данных, применяемой в большинстве методов машинного обучения [10], можно считать следующую:

• •    источник данных e - многомерная случайная величина с заданным распределением;

• •    обучающая выборка G teach = {( g _{( 1 )} ,..., g ( n ) )} - выборка из генеральной совокупности, где g ( i ) попарно независимые случайные величины с распределением e .

Это означает, что моделью наблюдаемого контекста K = ( G teach , M , I ) является выборка из генеральной совокупности K * = ( G , M , I ), где каждый g g G_teach представлен многомерной бернуллиевской случайной величиной. Однако, задача классификации должна по-преждему пониматься в смысле исходного контекста K * , образующего генеральную совокупность объектов. В таких условиях непротиворечивость логического вывода с помощью П ^ может быть нарушена, поскольку максимально специфические правила, извлеченные из наблюдаемого контекста K , зачастую не будут являться таковыми по отношению к истиному контексту K * .

Решить проблему противоречивости логического вывода возможно и в этом случае. Рассмотрим общий процесс преобразования набора литер. Пусть исходное множество литер B = B₁ проходит через цепочку преобразований B 1 ,..., B n (такие преобразования происходят со стартовым множеством B в алгоритме ProbClosure ). Предположим, что для алгоритма преобразования наборов литер существует некий критерий φ , минимизация которого определяет направление поиска в пространстве всех означиваний литер B g 2^{Llt( K} ) . Такие алгоритмы очень удобны в вычислительном плане, поскольку позволяют определить процедуру минимизация итеративно и свести исходную задачу к задаче минимизации.

Для процесса преобразований конфигураций верно, что если первый и последний наборы совпадают B 1 = B n , то он определяет тождественное преобразование, и тогда для критерия ф должно выполнятся определяемое ниже условие.

Определение 12 . Условие потенциальности

B 1 = B , ^ £ ф ( B„B , + , ) = 0.

i =1 ,..., n - 1

Функционал ф является аналогом физического потенциала. Условие в определении 12 является условием независимости потенциала от пути его вычисления, а, как известно, потенциал позволяет определить функцию энергии. Заметим, что идея введения функционала энергии не нова, в [11] она подробно изучена в контексте механизма обратной связи для глубинных нейронных сетей.

Теорема 3 [11]. Критерий ф может быть выражен с помощью потенциальной энергии E : ф ( B , C ) = E ( C ) - E ( B ) ; при этом ф ( B , C ) удовлетворяет условию потенциальности, а значение потенциала не зависит от точки начала отсчета энергии.

Зафиксируем некоторое множество правил ℜ . Далее будем считать что все правила R берутся из этого универсума правил ^ .

Определение 13 . Пусть R - правило, а B с Lit( K ) .

• •    R применимо (или R е App( B ) ) к набору литер B , если R ^ с B .

• •   R подтверждается (или R е Sat( B ) ) на наборе B , если R е App( B ) , и R ^ е B .

• •   R опровергается (или R е Fal( B ) ) на наборе B , если R е App( B ) , и — R ^ е B .

Определение 14 . Энергией противоречий мы называем функционал энергии, определенный с помощью веса опровергающихся правил, за вычетом энергии подтверждающихся правил:

E ( B ) = £ / (R)- £ y (R), y ( R ): ^^ [ 0 , ^ ) , ф ( B , 0 ) = E ( B ) .

R е Fal( B )         R е Sat( B )

Задача семейства алгоритмов состоит в том, чтобы минимизировать энергию противоречий E ( B ) ^ min , и, таким образом, найти максимально непротиворечивые комбинации литер (заметим, что можно также показать, что при наличии множества максимально специфичных правил алгоритм дает и абсолютно непротиворечивые комбинации литер, совпадающие с вероятностными формальными понятиями). Однако, полное решение задачи минимизации функционала энергии выглядит как полный перебор в пространстве означиваний литер 2^Lit( K ) .

Вспомним, что мы работаем в вероятностном контексте, где точного решения исходной задачи классификации не требуется, а приемлемость решения определяется иными способами (например, предсказательной точностью классификатора - Accuracy ). Поэтому абсолютной точностью при решении задачи минимизации функционала энергии можно пренебречь, а поставленная вычислительная проблема может быть решена субоптимальным образом. Предлагается вычислять приближенные решения посредством «жадного» итеративного алгоритма StatClosure , который минимизирует потенциал и выполняет поиск локально оптимальных решений соотношения E ( B ) ^ min . Свойство жадности опирается на то предположение, что для субоптимальности достаточно рассмотреть только потенциал перехода к ближайшим соседям, т.е. от конфигурации B к конфигурациям вида B ± l , где l е Lit( K ) .

Алгоритм 2 . StatClosure . Замыкание набора литер статистическим оператором вывода.

Вход : ^с For( K ) , K = ( G , M , I ) , B с Lit( K )

Выход : C с Lit( K ) - статистическое формальное понятие

1:  Функция StatClosure(K,^,B) 2:        B0 ^ B 3:         к ^ 0 4:        Повторять 5:               к ^ к + 1 6:                  Bk ^ Бк-1 7:              v ^ 0 8:               Candidates ^0 9: 10: 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21:

Для всех L ∈ Lit( K )\( B_{k 1} ∪ B_{k 1}) выполнять

Candidates ← Candidates ∪ { B k - 1 ∪ L }

Для всех L ∈ B_{k 1} выполнять

Candidates ← Candidates ∪ { B_{k 1} \ L }

Для всех C ∈ Candidates выполнять α ← φ ( B k - 1 , C )

Если α < ψ тогда

ψ ← α

B k ← C

Конец условия

Конец цикла

До тех пор пока ψ < 0

Вернуть B_k

22:    Конец функции

Полученные алгоритмом 2 неподвижные точки локально минимизируют функционал энергии противоречий, уменьшают количество противоречий до минимально возможного, а потому частично решают проблему противоречивости логического вывода.

2 Алгоритмы классификации

Рассмотрим некоторые модификации алгоритма StatClosure . Он не является точным обобщением алгоритма вероятностного замыкания ProbClosure . Чтобы понять, в чём отличие, рассмотрим момент добавления литеры в содержание понятия. Пусть к B_{s 1} была добавлена литера L_s , в результате чего получилось множество литер B_s = B_{s 1} + L_s . Тогда φ ( B_{s 1}, B_s ) из процедуры статистического замыкания представляет собой комбинацию γ -весов из сумм по следующим группам правил:

• 1) R ∈ Sat( B_s ) и R ^→ = L_s , то есть набор B_s подтверждает заключение правила R ;

• 2) R ∈ Fal( B_s ) и R ^→ = L_s , то есть B_s опровергает заключение правила R ;

• 3) R ∈ Sat( B_s ) и L_s ∈ R ^← , т.е. L_s делает посылку правила верной;

• 4) R ∈ Fal( B_s ) и L_s ∈ R ^← , т.е. L_s делает посылку верной и при этом R не верно на B_s .

Определение 15 . Обозначим правила, возникающие при рассмотрении литер-кандидатов на добавление к основному множеству литер B (первого и второго типов из перечисления выше) следующим образом:

• •   ConcSat( B , L ) =App( B ) ∩ { R : R ^→ = L };

• •   ConcFal( B , L ) =App( B ) ∩ { R : R ^→ = L };

• •   PreSat( B , L )=Sat( B + L ) ∩ { R : L ∈ R ^← };

• •   PreFal( B , L ) =Fal( B + L ) ∩ { R : L ∈ R ^← }.

Оператор замыкания из ProbClosure устроен таким образом, что использует только правила типов ConcSat . Однако в случае возникновения противоречий необходимо также учитывать и ConcFal. Поэтому модификация алгоритма StatClosure , наиболее близкая к

ProbClosure и учитывающая ConcSat и ConcFal, приводит к следующему потенциалу энергии противоречий:

ф( B s - 1 , B s - 1 u { L}) = E      Y( R ) -      E Y ( R ).

R e ConcFal( B_s , , L)          R e ConcSat( B_s , , L )

Замечание 1 . Следует отметить, что отображение ф уже не будет потенциалом в смысле определения 12. Однако алгоритм 2 по-прежнему применим после замены ф^ ф . Модификацию алгоритма с учетом модификации потенциала непротиворечивости определим как ConcConcepts .

Рассмотрим ещё одну модификацию алгоритма StatClosure. Раз имеются два различных алгоритма ConcClosure и StatClosure, имеющих одинаковую природу, то можно использовать их композицию. Самой простой является линейная комбинация а • StatConcep ts + (1 — а) • ConcConcep ts .

Для этого мы смешиваем потенциалы:

Ф а ( B , B + L ) = а • ^ Stat ( B , B + L ) + (1 — а ) • ф^ ( B , B + L ) =

« • [ E Y ( R ) — E Y ( R )] + E Y ( R ) — E Y ( R )

PreFal( B , L )           PreSat( B , L )            ConcFal( B , L )           ConcSat( B , L )

Определение 16 . Параметр в = 1/ а из формулы для ф назовем весом посылочных правил и обозначим как PremiseFactor .

Зачастую бывает желательно, чтобы проблема непротиворечивости решалась не только на уровне литер в описании понятия, но и на уровне правил, законов, которые это содержание описывают. В некоторых случаях допустим определённый уровень противоречий, определяемый количественным соотношением между подтверждающимися и опровергающимися правилами. В таком случае мы можем уменьшить вес правил, противоречащих добавлению литер. Это позволит добавлять в процессе выполнения процедуры замыкания больше литер, которые могут являться противоречивыми, но не более, чем того допускает выбранный уровень противоречивости w и, обратно, если требуется большая нетерпимость к противоречиям между различными правилами в логическом выводе, то уровень w следует увеличивать:

Фw (B, B + L ) = w •[ E Y( R) +   E  Y( R)] — [  E  Y( R) +   E  Y( R )] =

PreFal( B , L )         ConcFal( B , L )           PreSat( B , L )         ConcSat( B , L )

w • E Y ^{( R} ) ^— E Y^(R ).

Fal( B + L )          Sat( B + L )

Определение 17 . Параметр w из ф_w назовем весом противоречий.

Алгоритм StatClosure , а также его модификации с помощью веса посылочных правил и веса противоречий, могут успешно применяться для решения прикладных задач анализа данных аналогично тому, как для этого применяется АФП. Принципиальное отличие в том, что для применения алгоритма StatClosure и его модификаций не требуется безошибочность данных.

Рассмотрим применение алгоритма StatClosure и его модификаций к задачам классификации. Пусть K = (GT u GC, M и Л, I) есть контекст, представляющий собой выборку из генеральной совокупности, где GT - множество объектов обучения, а GC -множество объектов контроля, а Л - множество атрибутов разметки, определяющих класс объекта. Считаем, что роль учителя сводится к разметке объектов и присвоению им метки из множества классов Λ . Логику учителя можно сформулировать в виде отображения Teach : GT → Λ . Задача алгоритма классификации – доопределить отображение Teach на контрольном множестве GC в контексте KC = (GC,M,I ∩(GC ×M)) .

На первом этапе выполняется процедура кластеризации, обнаруживающая множество всех статистических формальных понятий на контексте K^T = ( G T , M оЛ , I n ( G T х ( M оЛ ) )) относительно одной из описанных выше вариаций StatClosure , которую мы условно обозначим за Closure( ⋅ ) :

ω = { Closure( g ^↑ ) g ∈ G^T } .

Далее классифицируемый объект поступает на обработку в процедуру ClassifyInCluster, описанную в алгоритме 3.

Алгоритм 3 . ClassifyInCluster . Классификация объекта.

Вход: g ∈ G^Control , Closure( ⋅ ), Ω

Выход: c ⊆ Λ – разметка объекта g

1:    Функция ClassifyInCluster (g, Closure, Ω) 2:      c←∅ 3:        B←g↑ 4:        B ^ C1osure(B) 5:       Если B е Q тогда 6:           c←B∩Λ 7:       Конец условия8:    Вернуть c9:    Конец функции

Алгоритм 3 и приводимый далее алгоритм 4, дают решение задачи классификации любым из описанных выше вариаций алгоритма StatClosure .

В [12] предлагается другой подход к задаче классификации. В работе решается задача распознавания транскрипционных факторов в последовательности ДНК. Идея заключается в том, чтобы определить степень принадлежности классифицируемого объекта ко всему спектру из найденных классов (кластеров).

Обратимся к определению 11 вероятностного оператора замыкания. Как нетрудно заметить, вероятностное формальное понятие полностью определяется множеством правил, которые его описывают. Действительно, по описанию прототипа класса B ⊆ Lit(K) можно найти уже знакомое нам множество правил Sat (B) . И обратно, по множеству правил ℜ можем построить прототип класса B = ∪ (R← ∪ R→) . Получаем эквивалентное определение R∈ℜ вероятностных формальных понятий через импликативные взаимосвязи.

Такое определение даёт возможность построить оценку близости классифицируемого объекта g к классу B , аналогично методам нечёткой кластеризации. Для этого следует ↑ вычислить значение энергии E(g ) относительно множеств правил Sat(B) каждого из классов. Тогда оценки принадлежности к классу будут следующими:

λ B ( g ^↑ )=     ∑    γ ( R ) -     ∑    γ ( R ) .

Л е Ра1( g ^Т ) n Sat ( B )          « e Sat( g ^Т ) n Sat ( B )

Алгоритм 4 выбирает два наиболее походящих класса B I и B II и в случае существенного смещения оценок принадлежности, задаваемого параметром λ * ≤ λ B ( ⋅ )/ λ B ( ⋅ ) , даётся ответ в зависимости от вхождения признаков разметки из Λ в описание класса B I .

Алгоритм 4 . ClassifyOverClusters . Классификация объектов.

Вход: g ∈ G^Control , Closure( ⋅ ), Ω

Выход: c ⊆ Λ – разметка классов для объектов g ∈ G Control

1:

2:

3:

4:

5:

6:

7:

8:

9:

10:

11:

12:

13:

14:

15:

16:

17:

18:

19:

20:

Функция ClassifyOverClusters ( K , ℜ , Ω ) ^λ Best , ^λ Second ^← 0

^B Best ^{, B} Second ^{← ⊥}

X ← g ^↑

X ← Closure( X )

Для всех B ∈ Ω выполнять

λ ← λ_B ( X )

Если λ > λ_Best тогда ^λ Best ^{← λ} B Best ← B

Иначе если λ > λ_Second

Second

В. л^в

Second

Конец условия

Конец цикла

Если ^{λ Best} ≥ λ тогда

λ

S eco n d

Вернуть B Best ∩Λ

Конец условия

Вернуть ∅

Конец функции

3    Данные репозитория UCI

В последнее время активно изучается тематика построения базисов ассоциативных правил [13], анализа зашумленных контекстов [2, 3, 6], и эффективной классификации [4, 5] в рамках направления АФП. Все эти задачи в той или иной степени могут быть отнесены к анализу данных, поэтому представляется важным сопоставить эти методы анализа формальных понятий с предлагаемыми методами классификации, основанными на вероятностных формальных понятиях (ВФП). Для сравнения была выбрана статья [7], в которой метод классификации заключается в построении особого рода решающих деревьев на основе концептуальных решеток (обозначим его как TreeFCA).

Основным источником данных является UCI [14]. К его преимуществам можно отнести обширные библиографические списки, группированные по наборам данных, а также широкую распространённость предлагаемых наборов данных в литературе.

Сравнение с [7] проводилось на следующих данных:

• 1)    zoo – содержит 17 булевозначных признаков, каждый из которых описывает отдельный аспект строения животной особи. Последний признак задаёт класс животных, к которому особь принадлежит (целочисленное значение от 1 до 7);

• 2)    kp-vs-kr – содержит шахматные эндшпили типа король+ладья против король+пешка. Каждый атрибут описывает какую-либо особенность позиции (например, близость белого короля к черной пешке) и является номинальным. Целевой признак описывает класс: белые могут выиграть (win), или белые не могут выиграть (nowin);

• 3)    votes – репозиторий включает бюллетени опросов (каждый состоял из 16 граф) респондентов, принадлежащих к двум политическим партиям (республиканцы и демократы). В данных присутствуют пропуски, которые были проинтерпретированы как шумы и дополнены случайными значениями; в остальном исходные данные содержат булевы признаки, которые удобно было представить в виде формального контекста. Обработанный набор представляет собой контекст K = ( G , M ∪ C , I ) , где | G |= 435 , | M |= 16 и C = { m_class }, gIm ⇔ данные содержат “yes” для выбранного респондента g в графе m .

Для решения задач классификации были использованы алгоритмы ClassifyInCluster и ClassifyOverClusters . Для исследования точности ( Accuracy ) использовалась техника кроссвалидации [4], при которой исходные данные делятся на N равномерных частей, и каждая часть используется в качестве контрольной выборки, в то время как остальная часть – в качестве обучающего контекста. Оценка точности предсказаний Accuracy на каждой отдельной выборке равнялась отношению правильно предсказанных классификатором классов к общему количеству объектов в контрольной выборке за вычетом отказов от классификации. Итоговая оценка Accuracy равна средней оценке точности по всем итерациям.

4    Результаты классификации

Эксперимент по классификации состоял из двух частей: обучения и контроля. На этапе обучения были задействованы алгоритмы семантического вероятностного вывода [15] для получения множества статистически значимых правил. StatConcepts выявил множества статистических формальных понятий, а дальнейшая процедура классификации выполнялась алгоритмами ClassifyInCluster и ClassifyOverClusters из раздела 3. Для тяжелых вычислений, таких как поиск множества статистически значимых правил, были задействованы мощности Сибирского суперкомпьютерного центра [16].

Вся выборка разбивалась на N частей для использования техники Cross-Validation. Параметр N немного отличается для различных наборов данных; точное значение указано в таблице 1. В столбцах указаны наборы анализируемых данных, количество итераций с различными разбиениями исходного множества объектов на обучающее GT и контрольное GC, процент верно и неверно предсказанных классификатором объектов суммарно по всем итерациям.

Результаты приведены в виде двух таблиц. В таблице 1 указаны характеристики применения методов ClassifyInCluster и ClassifyOverClusters к различным наборам данных из репозитория UCI [14]. Сравнение с [7] сведено в таблицу 2, куда включены результаты точности альтернативных алгоритмов C4.5, ID3, TreeFCA из указанной статьи.

С целью изучения гибкости алгоритмов на репозитории votes [7] была проведена дополнительная серия экспериментов по изучению модификаций процедуры замыкания из раздела 3. Классификация включала в себя серию экспериментов, в течение которой видоизменялось либо семейство используемых для классификации алгоритмов (выбирались разные процедуры Closure в алгоритме ClassifyInCluster), либо какие-то их параметры. Основным измеряемым показателем является точность предсказаний (Accuracy), а также количество отказов (Declined) алгоритма от прогнозов.

Таблица 1 – Протокол экспериментов по классификации методами ClassifyInCluster (In) и ClassifyOverClusters (Over) на репозиториях UCI

		Значения показателей
Репозиторий		zoo	kp_vs_kr	votes
Метод		In	Over	In
Показатели	Итераций	101	20	42
	Объектов	101	1790	420
	Отказов	5%	25.98%	47.62%
	Верно	92%	60.50%	50.71%
	Неверно	3%	13.52%	1.67%

Таблица 2 – Точность различных алгоритмов на наборах данных из UCI

		Точность алгоритмов
Репозиторий		zoo	kp_vs_kr	votes
Алгоритмы	ВФП	96.84%	81.74%	96.82%
	C4.5	92.69%	72.78%	86.50%
	ID3	95.04%	74.50%	89.28%
	TreeFCA	96.04%	74.65%	90.5%

Результаты экспериментов приведены на рисунке 1, где, в частности, видно, что алгоритмы обладают различными качественным свойствами, а результаты, полученные с их помощью, хорошо локализованы.

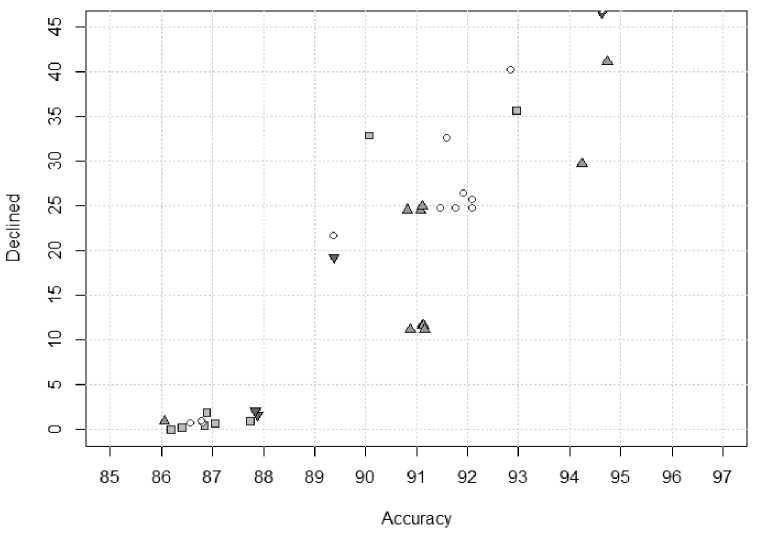
Рисунок 1 – Характеристики выполнения различных модификаций процедуры Closure при классификации данных votes :  - эксперименты близкие к методу ConcConcepts ;

• -    эксперименты с применением метода StatConcepts ;

• -    эксперименты смешанного метода с единичным весом противоречий;

• - все остальные эксперименты

Заключение

Вероятностный подход к определению формальных понятий позволяет определить целое семейство алгоритмов кластеризации, смягчая проблему противоречивости логического вывода как для полностью определенных данных (формальных контекстов), так и для выборок из генеральной совокупности.

Алгоритмы классификации ClassifyInCluster и ClassifyOverClusters , построенные на основе статистических формальных понятий, позволяют успешно решать достаточно сложные задачи классификации, что было продемонстрировано на ряде наборов данных репозитория UCI, где они могут соперничать на равных с разработками АФП и классическими алгоритмами на основе решающих деревьев, имея в некоторых случаях ощутимое преимущество.

Статистические формальные понятия оказываются простыми в построении и полезными в прогнозировании. В то же время параметризация алгоритмов и их различные модификации обеспечивают необходимую гибкость при анализе данных. Заметна перспектива развития предлагаемого метода в рамках направления интеллектуального анализа данных: для этого следует провести более масштабные эксперименты, а также произвести интеграцию с уже существующими инструментами хранения и анализа данных.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант РФФИ 15-07-03410.