Вероятностные оценки массовых характеристик энергодвигательных систем транспортных и транспортно-энергетических космических аппаратов

евдокимов р.а.

синявский в.в.

скребков с.а.

СКРЕБКОВ Сергей Александрович — доктор технических наук, ветеран ВКА им. А.Ф. Можайского SKREBKOV Sergey Alexandrovich — Doctor of Science (Engineering), Veteran of Mozhaysky VKA

Решение многих перспективных задач космонавтики требует создания принципиально новых транспортных, а также транспортно-энергетических космических аппаратов (КА) — межорбитальных буксиров (МБ) и транспортно-энергетических модулей (ТЭМ) [1]. Эффективность указанных космических средств в первую очередь будет определяться степенью совершенства их энергодвигательных систем (ЭДС), по сути, МБ и ТЭМ представляют собой ЭДС, обличенные в конструкцию [2]. В состав ЭДС данных КА должны входить энергетические установки (ЭУ) (ядерные, либо солнечные), а также электроракетные двигательные установки (ЭРДУ) большой мощности (сотни киловатт – мегаватты) [3, 4]. Соответственно, эффективность выполнения целевых задач МБ и ТЭМ будет в значительной мере определяться показателями качества энергетических и двигательных установок, включая их массовые характеристики. Поскольку мощные ЭУ и ЭРДУ, фактически, должны создаваться параллельно с разработкой МБ и ТЭМ, то на ранних этапах проектирования (когда осуществляется выбор структуры и проектных параметров ЭДС и КА в целом) могут быть сделаны только оценки их массовых характеристик. Влияние на процесс создания ЭУ и ЭРДУ множества факторов

(объема и стабильности финансирования, уровня квалификации персонала, появления новых технологий, результатов НИОКР по отработке ключевых технологий и систем и т. п.), часть из которых случайна, приводит на ранних этапах проектирования к большому разбросу оценок возможных значений массовых характеристик. Во избежание грубых ошибок при оценке эффективности создаваемых КА, а также выборе структуры и проектных параметров их ЭДС, данное обстоятельство должно непременно учитываться.

Один из возможных подходов состоит в использовании вероятностного описания оценок массовых характеристик, т. е. рассмотрении масс (удельных масс) элементов ЭДС как случайных величин. Данный подход особенно уместен, если для выбора структуры и проектных параметров ЭДС МБ (или ТЭМ) применяется методология комплексной оптимизации ЭДС КА, предполагающая использование в качестве показателя эффективности вероятности выполнения ЭДС своей задачи [2, 5]. Могут использоваться и другие подходы, подразумевающие стохастическое описание массовых характеристик элементов ЭДС, например, теория полезности.

Вероятностное описание массовых характеристик предполагает отыскание соответствующих законов распределения.

Обоснование вида законов распределения оценок массовых характеристик элементов ЭДС перспективных КА

Обоснование вида законов распределения случайных величин, описывающих оценки массовых характеристик элементной базы ЭДС перспективных КА, а также нахождение параметров данных законов — задача, решить которую методами математической статистики не представляется возможным. Это объясняется отсутствием необходимого количества данных по проектным оценкам характеристик перспективных двигательных и энергетических установок. Так, количество выполненных проектных проработок мощных термоэмиссионных космических ядерных энергоустановок (КЯЭУ) типа КЯЭУ буксира «Геркулес» не превосходит нескольких десятков для всех уровней мощности. Между тем, оценки массовых характеристик КЯЭУ должны быть даны с учетом зависимости от проектной мощности установки. Соответственно, закон распределения массы (удельной массы) должен быть найден для различных уровней проектной мощности, для каждого из которых имеется всего лишь несколько оценок. В этой связи практически незаменимыми для нахождения параметров законов распределения массовых характеристик являются методы экспертных оценок, зарекомендовавшие себя при оценке качества сложных технических систем и изделий [6–9]. Однако вид закона распределения оценить подобным образом значительно сложнее: требуется либо привлечение большого количества (сотен) экспертов, которые должны дать прямую оценку массы элемента ЭДС для различных уровней его проектной производительности с последующей статистической обработкой полученных данных, либо непосредственный опрос меньшей группы экспертов относительно характера закона распределения. Учитывая, что число квалифицированных специалистов, работающих в области проектирования КЯЭУ и ЭРДУ большой мощности, сравнительно невелико, первый подход представляется не просто трудоемким, но и практически не реализуемым. Второй подход ведет либо к субъективному, либо противоречивому результату, поскольку вероятностные оценки представляют для большинства экспертов значительные трудности. С учетом вышесказанного выбор вида закона распределения массовых характеристик элементов энергодвигательного комплекса многоразовой транспортной системы должен базироваться на опыте системно-технических исследований, эвристических подходах, а также применении предельных теорем теории вероятностей. В литературе по моделированию сложных технических систем рекомендуется использовать для вероятностного описания характеристик элементов усеченный нормальный закон распределения, треугольный закон, а также β-распределение [9]. Использование усеченного нормального закона оправдано тем, что большинство элементов можно рассматривать также в качестве сложных систем, включающих множество субэлементов, на характеристики которых оказывает влияние множество сравнительно независимых факторов. Масса элемента оказывается распределенной по закону, близкому к нормальному, а с учетом физических ограничений и практически важного диапазона значений — усеченному нормальному закону [9].

Необходимо также отметить, что массовые характеристики элементов ЭДС КА оказывают влияние на эффективность выполнения КА своих задач. Масса КА является суммой масс отдельных систем КА, включая элементы ЭДС. При этом соблюдается условие независимости масс отдельных элементов. В связи с этим оценка массы КА будет распределена по закону, близкому к нормальному, даже при некотором отклонении от нормального закона распределения масс отдельных элементов.

Таким образом, принимается допущение о распределении оценок масс элементов ЭДС перспективных КА по усеченному нормальному закону.

Если данный закон является симметричным относительно математического ожидания, то для оценки параметров распределения массы элемента ЭДС может быть использовано правило «трех сигма» [10]:

М [ м_el ] = ( М¹™ + _М’тх )/2; (1)

σ М ≈ ( М™” ■^el ' )/6, (2)

где М [ м_el ] — математическое ожидание; σ — среднеквадратическое отклонение; М™^х , М"™ — максимальная и минимальная массы элемента ЭДС КА, соответственно.

Для отыскания закона распределения массы элемента ЭДС заданной проектной производительности требуется оценить только ее максимальное и минимальное возможные значения. Кроме того, для проверки предположения о симметричности распределения целесообразно дать экспертную оценку наиболее вероятного значения массы и сравнить его с величиной, полученной по формуле (1).

Таким образом, для определения параметров законов распределения случайных массовых характеристик элементов ЭДС КА рекомендуется применять метод экспертных оценок. Ниже представлена методика проведения экспертного опроса и статистической обработки его результатов на примере определения оценок массовых характеристик КЯЭУ большой мощности.

Объекты исследования

В настоящей работе представлены результаты применения метода экспертных оценок к определению характеристик следующих элементов ЭДС перспективных КА:

• •    однорежимных высокотемпературных термоэмиссионных КЯЭУ типа энергоустановки буксира «Геркулес» [3] электрической мощностью 150…1 000 кВт с ресурсом 5–7 лет;

• •    двухрежимных КЯЭУ аналогичного типа с мощностью 100…300 кВт на транспортном режиме продолжительностью до одного года, и 30…100 кВт на энергетическом режиме продолжительностью 7–10 лет.

Отношение мощности на транспортном режиме к мощности на энергетическом режиме N _К ^тр _ЯЭУ /N _К ^д _ЯЭУ ≈ 3 характерно для большинства применений двухрежимных КЯЭУ [11].

Компоновочные схемы КЯЭУ указанных типов представлены на рис. 1 и 2.

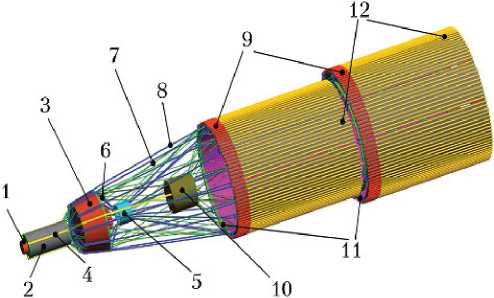
Рис. 1. Компоновочная схема КЯЭУ типа ЭУ МБ «Геркулес»: 1 — блок генераторов пара цезия и системы удаления газообразных продуктов деления; 2 — термоэмиссионный реактор-преобразователь (ТРП) модульной схемы; 3 — многослойная радиационная защита; 4 — сильноточная шина; 5 — многоканальный МГД-насос с общей магнитной системой всех модулей; 6 — трубопровод литиевой системы охлаждения на входе в модуль ТРП; 7 — опорная ферма; 8 — трубопровод литиевой системы охлаждения на выходе из модуля ТРП; 9 — теплообменник литий–натрий зоны испарения тепловой трубы; 10 — силовой преобразовательный блок (высоковольтные кабели не показаны); 11 — опорное кольцо (раздвижная ферма полезной нагрузки не показана); 12 — зона конденсации тепловых труб холодильника-излучателя

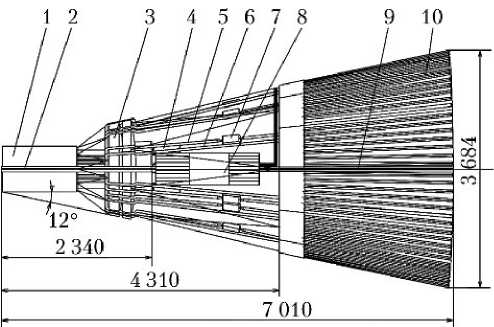
Рис. 2. Компоновочная схема термоэмиссионной КЯЭУ мощностью 200 кВт: 1 — термоэмиссионный реактор-преобразователь; 2 — низковольтная шина; 3 — радиационная защита КЯЭУ; 4 — привод системы управления и защиты; 5 — холодный трубопровод; 6 — горячий трубопровод; 7 — электромагнитный насос; 8 — преобразователь напряжения; 9 — высоковольтная шина; 10 — холодильник-излучатель

Методика получения оценок массовых характеристик КЯЭУ по результатам экспертного опроса

Для определения минимальных, максимальных и наиболее вероятных значений масс указанных выше КЯЭУ с различным уровнем мощности непосредственно использовался метод экспертных оценок. С целью исключения конформизма в оценках, а также с учетом работы с представителями нескольких организаций была выбрана индивидуальная форма опроса в виде анкетирования. Отбор экспертов, составление анкеты и проведение опроса, обработка его результатов выполнялись в соответствии с рекомендациями работы [6].

Рекомендуемое количество экспертов для получения достаточно точных оценок при разумных трудозатратах должно быть в пределах 7…15 чел [6–9]. Учитывая относительно малое количество высококвалифицированных специалистов, занятых в исследуемой области, и уникальность объектов исследования, в группу для оценки массовых характеристик КЯЭУ третьего поколения было включено восемь экспертов. При этом выбор конкретных специалистов был обусловлен их непосредственным участием в работах над КЯЭУ рассматриваемого типа, а также уровнем их квалификации. В итоге в группу вошли специалисты РКК «Энергия» (как головной организации по работам над КЯЭУ типа ЭУ буксира «Геркулес», а также КА на их основе) и МГТУ им. Н.Э. Баумана.

В опросной анкете экспертам было предложено дать ответ на вопрос о максимальном, минимальном и наиболее вероятном значениях масс однорежимных КЯЭУ мощностью 150, 300, 600 и 1 000 кВт, а также двухрежимных КЯЭУ мощностью 100/30, 150/50 и 250/80 кВт. Анкета содержала также вопросы, необходимые для оценки степени компетентности экспертов (см. ниже) — о стаже работы в отрасли, количестве научных публикаций и/или патентов, должности, наличии ученых степеней и званий.

Полученные в ходе экспертизы результаты были подвергнуты статистической обработке [7].

Оценки, назначенные экспертами каждой исследуемой величине, осреднялись с учетом коэффициентов компетентности экспертов по формуле:

1 ^m

^Wj ^{Г = m}    ∑ ^Wj^{i k} Э i^{,           (3)}

∑k i = 1 i = 1 Эi где — оценка i-ым экспертом j-й величины;

• —    групповая оценка j -й величины; k _{Э i} — коэффициент компетентности i -го эксперта; m — количество экспертов в группе.

Назначение оценок экспертами можно рассматривать как измерение некоторой величины несколькими приборами, имеющими различную точность, которая и характеризуется коэффициентами компетентности экспертов [7]. Среди методов учета компетентности экспертов широкое распространение получил статистический, в соответствии с которым коэффициенты k _{Э i} уточняются в процессе обработки результатов в зависимости от величины отклонения оценки, назначенной данным экспертом, от средней в группе. Тогда коэффициенты компетентности можно представить в следующем виде:

ma

Э i      Э i Э i ^,

где ,    — статистический и априорный коэффициенты компетентности эксперта.

Априорный коэффициент должен оцениваться, исходя из сведений об экспертах, по искусственной шкале от 0 до 1. В рамках настоящей работы используется шкала, представленная в табл. 1.

Статистический коэффициент компетентности рассчитывается по формулам:

H j =

w ^; - ^ Г jj

w Г j

₁ n _в ^m Э ⁱ 1 ⁼ n ∑ ^Hj^{i ;}

в j = 1

_km ₌

Эi           i , mЭ1

где — относительное отклонение индивидуальной оценки i -ым экспертом j -й величины от ее групповой оценки; n _в — количество величин, оцениваемых данной группой экспертов; ^m — статистический коэффициент компетентности i -го эксперта данной группы.

Очевидно, что расчет коэффициентов ^m по формулам (5–7), а также групповой оценки каждой величины по формуле (4) должен носить итерационный характер. На первой итерации принимается ^m = 1 для всех экспертов, с помощью формул (3, 4) рассчитываются первые приближения групповых оценок величин. Затем находятся новые значения ^m по формулам (5–7) и новое приближение групповых оценок по соотношениям (3, 4).

Условная шкала априорной компетентности экспертов

Таблица 1

Значение априорного коэффициента компетентности эксперта, k Э а	Критерии сравнения экспертов
	Стаж работы в отрасли, лет	Количество публикаций и/или патентов	Ученая степень и/или должность
0	< 3	< 5	—
0,3	< 10	< 15	—
0,35	< 10	< 30	—
0,45	< 10	< 30	Кандидат наук/нач. сектора
0,65	< 15	< 30	Кандидат наук/нач. сектора
0,75	< 15	< 60	Кандидат наук/нач. сектора
0,85	< 15	< 60	Доктор наук/нач. отдела
0,9	< 15	< 100	Доктор наук/нач. отдела
0,9	> 20	> 100	Кандидат наук/нач. сектора
0,95	< 20	< 100	Доктор наук/нач. отдела
1	> 20	> 100	Доктор наук/нач. отдела

Итерационный процесс должен продол- жаться до тех пор, пока не будет выполнено условие:

зовать коэффициент согласованности E , являющийся разновидностью коэффициента множественной корреляции:

^ Г( l ) - Н 'Ь l -1) W ^Г( l¹

< е, (8)

E =

m ² ( n _в - 1)

n в m

j = 1 i = 1

—

W i - W ² ji

где Wp \ Ну^{( 1 -1)} — групповые оценки j -й величины на l -ой и ( l –1)-й итерациях; ε — требуемая точность расчета.

Для полученных групповых оценок должны быть построены доверительные интервалы с целью определения точности и проверки на значимость. В соответствии с методикой обработки результатов неравноточных измерений (в качестве показателя точности выступает коэффициент компетентности эксперта) [7]:

–    1 nв где Wi =    ∑Wji ;

ⁿ в j = 1

ⁱ s _Э

( n _в – 1)

_∑ ^{n в} ( W_j ⁱ – W ^– _i ) ² .

j = 1

1         m sj--х     Z( Wj — W,r )2 k Э i■    (9)

( m – 1) ∑ _k ^{i = 1}

i -1 ^Э i

где — оценка дисперсии j -й величины.

Доверительный интервал групповой оценки j -й величины определяется и квантилем распределения Стьюдента t_j , соответствующим заданной доверительной вероятности и числу степеней свободы,

Вычисленное значение коэффициента согласованности проверяется на значимость. С этой целью вычисляется значение коэффициента Пирсона: = m ( n _в – 1) E . Сравнивая полученное расчетное значение с табличным ( ), соответствующим числу степеней свободы ( n _в – 1), можно сделать вывод о значимости величины E : если ≥ , то коэффициент согласованности значим, а оценки экспертов согласованы.

равному ( m – 1):

∆ =   s ² t = s t .

j j j j j

Считается, что оценка незначима , если Δ _j > .

Для оценки достоверности полученной информации важно оценить степень согласованности экспертов. Можно исполь-

Результаты экспертного опроса о значениях массовых характеристик КЯЭУ и их статистической обработки

В табл. 2 приведены результаты опроса экспертов по массовым характеристикам (минимальному, максимальному и наиболее вероятному значениям массы КЯЭУ —

,       ,       , соответственно) одно режимных КЯЭУ большой мощности с ресурсом 5–7 лет.

Таблица 2

Результаты опроса экспертов по массовым характеристикам однорежимных КЯЭУ с ресурсом 5–7 лет (индивидуальные оценки)

S4^ m	ka Э i	Проектная мощность КЯЭУ, N п К р ЯЭУ , кВт
		150			300			600			1 000
		min m КЯЭУ,кг	/Икяэу, кг	max m КЯЭУ,кг	min m КЯЭУ,кг	т кяэу , кг	max m КЯЭУ,кг	min m КЯЭУ,кг	т кяэу , кг	max m КЯЭУ,кг	min m КЯЭУ,кг	т кяэу , кг	max m КЯЭУ,кг
1	0,75	4 000	5 500	7 000	5 000	7 500	10 000	6 000	10 000	14 000	8 000	12 000	16 000
2	1	4 000	4 200	5 000	5 000	5 200	7 000	6 000	7 000	9 000	8 000	10 500	12 000
3	0,9	5 000	5 500	6 000	6 200	6 700	7 200	7 600	8 100	8 600	9 500	10 000	10 500
4	0,9	5 000	6 500	8 000	6 000	8 000	10 000	7 000	9 500	12 000	9 000	12 000	15 000
5	0,9	6 000	6 500	7 000	7 000	7 500	8 000	8 500	10 500	11 000	10 000	12 000	14 000
6	1	10 000	12 000	12 000	15 000	18 000	18 000	—	—	—	—	—	—
7	0,9	2 400	3 200	4 000	3 700	4 400	5 000	5 500	6 300	7 000	9 000	11 000	13 000
8	0,8	2 600	3 500	4 600	4 700	6 700	8 200	8 000	12 000	15 000	11 200	16 000	18 000

Таблица 3

Оценки массовых характеристик однорежимных КЯЭУ по результатам экспертного опроса (групповые оценки)

Групповые оценки массовых характеристик КЯЭУ, кг	Проектная мощность КЯЭУ, N К пр ЯЭУ , кВт
	150	300	600	1 000
min КЯЭУ	4 430±832	5 577±729	6 963±784	9 077±738
м КЯЭУ	5 260±878	6 724±888	8 765±1 218	11 355±1 181
max КЯЭУ	6 201±979	8 087±1 029	10 439±1 654	13 270±1 622

Таблица 4

Результаты опроса экспертов по массовым характеристикам двухрежимных КЯЭУ (индивидуальные оценки)

m	ka Э i	Проектная мощность КЯЭУ, N К тр ЯЭУ / N К д ЯЭУ , кВт
		100/30			150/50			250/80
		m К m Я in ЭУ, кг	МКЯЭУ , кг	max m КЯЭУ,кг	min m КЯЭУ ,кг	МКЯЭУ , кг	max m КЯЭУ,кг	min m КЯЭУ,кг	m КЯЭУ , кг	max m КЯЭУ,кг
1	0,75	4 000	5 000	6 000	5 000	6 500	8 000	6 000	7 500	9 000
2	1	3 000	3 200	4 000	4 000	4 500	5 000	4 500	5 000	6 000
3	0,9	3 700	5 000	10 000	4 600	8 000	12 000	6 200	11 000	15 000
4	0,9	5 000	6 500	8 000	6 500	7 500	9 000	6 500	8 500	10 000
5	0,9	6 000	6 500	7 000	6 500	7 500	8 000	7 000	9 000	12 000
6	1	6 000	9 000	10 000	10 000	12 000	12 000	14 000	16 000	16 000
7	0,9	2 300	3 000	3 600	3 300	3 900	4 700	4 200	4 800	5 500
8	0,8	1 900	2 800	3 400	2 500	3 300	4 500	3 800	5 400	6 500

Таблица 5

Оценки массовых характеристик двухрежимных КЯЭУ по результатам экспертного опроса (групповые оценки)

Групповые оценки массовых характеристик КЯЭУ, кг	Проектная мощность КЯЭУ, Nтр / Nд , кВт , К ЯЭУ КЯЭУ,
	100/30	150/50	250/80
min КЯЭУ	4 890±638	6 226±804	6 548±976
м КЯЭУ	6 193±781	7 339±889	8 591±1 183
max КЯЭУ	7 646±980	8 726±1 075	10 348±1 428

В табл. 3 представлены результаты обработки полученных данных — групповые оценки с доверительными интервалами, рассчитанные по формулам (4–10). Аналогичные результаты были получены для двухрежимных КЯЭУ (табл. 4 и 5). Приведенные в табл. 3 и 5 интервалы групповых оценок соответствующих масс КЯЭУ вычислялись для доверительной вероятности 0,9.

Как видно из табл. 2 и 4, индивидуальные оценки экспертов имеют значительный разброс для отдельных величин.

Это обусловлено различными взглядами на пути обеспечения заданного ресурса КЯЭУ (возможность использования перспективных материалов в конструкции электрогенерирующих каналов, либо снижение плотности мощности), а также — на значения масс отдельных систем КЯЭУ.

В частности, высокие значения масс КЯЭУ, присвоенные экспертом № 6, обусловлены возможностью реализации больших значений массы системы преобразования электрической мощности КЯЭУ. Эта система обеспечивает преобразование постоянного тока низкого напряжения (100–120 В), вырабатываемого термоэмиссионным реактором-преобразователем (ТРП), в ток высокого напряжения, потребляемый ЭРДУ (сотни – тысячи вольт) [12]. Тем не менее, групповые оценки масс являются значимыми — величины Δj составляют 12–18% от соответствующих оценок. Коэффициент согласованности экспертов, рассчитанный по формуле (11), при оценке массовых характеристик однорежимных КЯЭУ составил 0,942, а двухрежимных — 0,908. Оценка по критерию Пирсона подтвердила значимость указанных величин этого коэффициента.

Выполненные оценки подтверждают симметричный характер распределения. Относительные отклонения групповых оценок наиболее вероятных значений масс КЯЭУ от средних между ^КЯЭУ и ^КЯЭУ находятся в пределах 0,7…1,8% как для однорежимных, так и для двухрежимных КЯЭУ во всем диапазоне проектной мощности, т. е. отклонения находятся в пределах точности оценок.

Зависимости массовых характеристик КЯЭУ от уровня проектной мощности

В литературе по космической энергетике (например, [2, 13]) предложены детерминированные математические зависимости, позволяющие найти массу КЯЭУ различных типов для заданных значений проектной мощности. В том числе рассматриваются зависимости удельных масс КЯЭУ от их проектной мощности — γ _КЯЭУ ( N. пр ЭУ). Так, для всех поколений термоэмиссионных КЯЭУ в работе [13] на основе статистических данных предложена аппроксимационная зависимость, охватывающая широкий диапазон значений величины N пр _:

A

γКЯЭУ(NКЯЭУ) = пр + D, [кг/кВт], (12) BNКЯЭУ + С где A = 51,43; B = 0,01; C = 0,35; D = 4,85.

Зависимость (12) представлена графически на рис. 3, ее коэффициенты получены методом наименьших квадратов.

Данная зависимость является исключительно феноменологической, охватывая совершенно различные КЯЭУ термоэмиссионного типа, находящиеся на различном уровне разработки (от КЯЭУ, прошедших летно-конструкторские испытания, до аванпроектов). Среди этих КЯЭУ есть как однорежимные (с различным ресурсом), так и двухрежимные установки с длительным энергетическим режимом. Поскольку для двухрежимных КЯЭУ масса определяется транспортным режимом, данную зависимость можно рассматривать применительно к однорежимным КЯЭУ соответствующей мощности с ресурсом 1–3 года. Для однорежимных КЯЭУ с бóльшим ресурсом (5–7 лет и более), а также для двухрежимных КЯЭУ необходимо внесение поправок. Кроме того, формула (12) дает лишь детерминированную оценку удельной массы КЯЭУ для заданной проектной мощности.

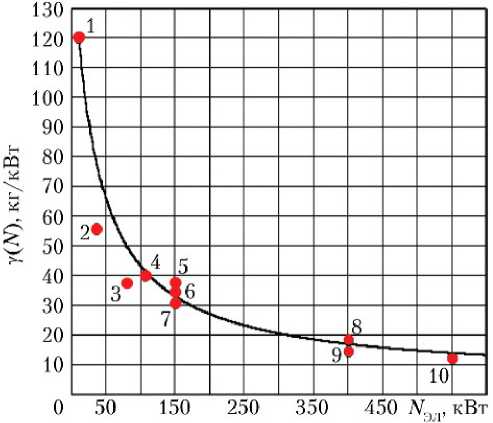
Рис. 3. Зависимость удельной массы КЯЭУ от проектной электрической мощности КЯЭУ [13]: 1 — КЯЭУ «Топаз»; 2 — ЯЭУ-25М; 3 — ЯЭУ-25; 4 — ЯЭУ-50; 5 — ЯЭУ-100; 6 — ЯЭУ-100 (теплоноситель — Li); 7 — двухрежимная КЯЭУ на основе технологии КЯЭУ буксира «Геркулес»; 8 — ЯЭУ-400; 9 — «Топаз-ВРТ»; 10 — КЯЭУ буксира «Геркулес»

В рамках данной работы предлагается следующий подход к вероятностной оценке массы КЯЭУ в зависимости от ее проектной мощности. Для каждого значения N. пр масса КЯЭУ может быть представлена как случайная величина, распределенная по усеченному нормальному закону с параметрами, вычисляемыми по формулам, аналогичным соотношениям (1) и (2):

M [ М _КЯЭУ ] = ( ^КЯЭУ + ^КЯЭУ)/2;    (13)

σ ≈ ( ^КЯЭУ –      )/6,       (14)

КЯЭУ где M[мКЯЭУ] — математическое ожидание; σ — среднеквадратическое отклонение;

■^КЯЭУ , ^КЯЭУ — максимальная и минимальная массы КЯЭУ для заданной проектной мощности, соответственно.

Величины ^^КЯЭУ и М™.” оцениваются для нескольких значений пр методом экспертных оценок (см. выше). Полученные значения используются для построения зависимостей ( пр ),       ( пр ), вид которых принимается аналогичным (12), с учетом того, что Mкяэу = YкяэyjVпрзу, но с другими коэффициентами, найденными методом наименьших квадратов. Далее, для любого произвольного значения пр , пользуясь полученными зависимостями, можно найти ( пр ),       ( пр ), а по формулам (13)

и (14) — параметры закона распределения массы КЯЭУ для данной проектной мощности.

Посредством метода наименьших квадратов на основе групповых оценок, представленных в табл. 3 и 5, были получены коэффициенты для функциональных зависимостей, аналогичных (12), для вычисления минимальных, максимальных и наиболее вероятных значений удельных масс КЯЭУ — - ^ у), - ^р _эу), r^ MX, _У), соответственно. Данные коэффициенты приведены в табл. 6.

Таблица 6

Значения коэффициентов аппроксимации в зависимостях удельной массы КЯЭУ от проектной электрической мощности

Вид зависимости удельной массы	Тип КЯЭУ
	Однорежимные КЯЭУ				Двухрежимные КЯЭУ
	А	В	С	D	А	В	С	D
Ymin (Ы пр ) ' КЯЭУv КЯЭУ7	39,46	0,0081	0,343	4,27	52,23	0,0029	0,518	–14,66
..max / 1 г ,   х ( пр  )	35,60	0,0047	0,310	6,04	55,35	0,0067	0,183	11,64
( пр )	49,27	0,0086	0,390	5,85	49,74	0,0042	0,378	–0,78

Максимальные отклонения расчетных значений, полученных по формуле (12) для приведенных в табл. 5 и 6 коэффициентов, от групповых экспертных оценок составляют менее 2%, что находится в пределах погрешности оценок. Несмотря на существенные отличия в значениях коэффициентов (что характерно для аппроксимации гиперболическими функциями), зависимости удельных масс от проектной мощности имеют сходный вид и представлены на рис. 4 и 5.

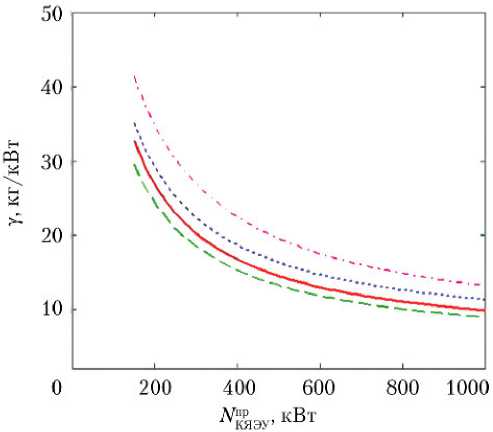
Рис. 4. Зависимость удельной массы однорежимных КЯЭУ типа ЭУ буксира «Геркулес» с ресурсом 5–7 лет от проектной электрической мощности: — — — минимальная оценка удельной массы КЯЭУ Указу ^(jVпрэу) ; — - оценка, вычисленная по формуле (12); — — — — оценка наиболее вероятного значения удельной массы КЯЭУ ( ^пр ) ; — — — — максимальная оценка удельной массы КЯЭУ ( ^пр )

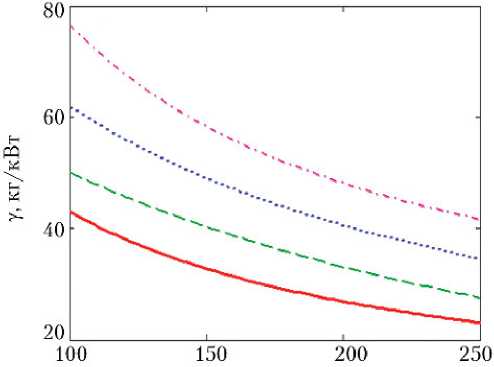
№р , кВт

КЯЭУ’

Рис. 5. Зависимость удельной массы двухрежимных КЯЭУ типа ЭУ буксира «Геркулес» от электрической мощности на транспортном режиме: — — оценка, вычисленная по формуле (12); — — — минимальная оценка удельной массы КЯЭУ Укяэу -^ тя-»■) ; ^- “ “ — оценка наиболее вероятного значения удельной массы КЯЭУ ( ^т ) ; — — — — максимальная оценка удельной массы КЯЭУ ( ^т )

Полученные зависимости позволяют найти ( пр ), ( пр ) и воспользоваться далее формулами (13) и (14) для отыскания параметров закона распределения оценки массы КЯЭУ для любого значения проектной мощности.

Полученные групповые оценки для наиболее вероятных значений масс однорежимных КЯЭУ превосходят значения масс КЯЭУ аналогичного уровня мощности, вычисленные по формуле (12), на ~7–15% (расхождение возрастает для бóльших мощностей).

Несмотря на то, что данное расхождение укладывается в границы доверительных интервалов сделанных оценок, оно должно являться действительным в связи со своим систематическим характером для разных значений уровня мощности. Групповые оценки математических ожиданий масс двухрежимных КЯЭУ выше значений, полученных расчетом по формуле (12) (в качестве проектной мощности используется мощность на транспортном режиме), на 44–50%.

Указанные отличия ожидаемы, так как оценки давались для КЯЭУ с бóльшим ресурсом. Для двухрежимных КЯЭУ умеренной мощности имеет значение также то, что они должны создаваться ранее однорежимных КЯЭУ мощностью свыше 300 кВт, с использованием меньшей доли инновационных технологий и материалов, что обусловливает больший консерватизм оценок со стороны экспертов.

выводы

На ранних этапах проектирования перспективных транспортных КА целесообразно использовать вероятностное описание оценок массовых характеристик элементной базы их ЭДС. Рекомендуется использование усеченного нормального закона распределения, параметры которого могут быть найдены методом экспертных оценок. В рамках настоящей работы предложена соответствующая методика, предполагающая статистическую обработку результатов экспертного опроса. Представлены результаты применения данной методики к оценке массовых характеристик однорежимных и двухрежимных термоэмиссионных КЯЭУ большой мощности. Предложены аппроксимационные зависимости, позволяющие найти максимальные и минимальные оценки удельных масс КЯЭУ указанных типов для заданных значений проектной электрической мощности. Эти значения позволяют отыскать математическое ожидание и среднеквадратическое отклонение оценки массы КЯЭУ для заданной проектной мощности.