Вершинные и рёберные усечения закрытых простых форм: к 280-летию Ж. Б. Л. Роме-де-Лиля и 80-летию Н. П. Юшкина

Автор: Войтеховский Ю.Л., Степенщиков Д.Г.

Статья в выпуске: 5 (257), 2016 года.

Бесплатный доступ

В 2016 г. исполняется 80 лет со дня рождения Н. П. Юшкина - нашего современника, при жизни ставшего классиком отечественной минералогии. Одна из оригинальных черт его научного стиля - умение извлекать забытые идеи из старинных фолиантов, казалось бы, имеющих сугубо исторический интерес. Яркое тому свидетельство - препринт научного доклада [3], не теряющий свежести на протяжении трёх десятилетий. Беря пример с учителя, авторы этой статьи решают задачу о вершинных и рёберных усечениях кристаллического полиэдра, оставленную нам одним из основателей кристалломорфологии - Ж. Б. Л. Роме-де-Лилем, которому в этом году исполняется 280 лет.

Еще

Закрытые простые формы вершинные усечения рёберные усечения, комбинации простых форм, геометрически дуальные формы

Короткий адрес: https://sciup.org/149128676

IDR: 149128676 | DOI: 10.19110/2221-1381-2016-5-32-37

Текст научной статьи Вершинные и рёберные усечения закрытых простых форм: к 280-летию Ж. Б. Л. Роме-де-Лиля и 80-летию Н. П. Юшкина

Сегодня кристаллический полиэдр рассматривают с точки зрения взаимного расположения граней, что обусловлено законом постоянства углов и гониометрической техникой измерений. Но так было не всегда. А. Г. Вернер различал кристаллы по вершинам [2], а Ж. Б. Л. Роме-де-Лиль отдавал должное всем элементам: «Какой-либо кристалл может быть усечённым в своих вершинах, а также вдоль рёбер. <_> Наблюдаются кристаллы, часть которых имеет усечения или на вершинах, или даже и на вершинах, и на рёбрах» [1, с. 13]. В этом рассуждении вполне просматривается «задача Роме-де-Лиля»: для данного кристаллического полиэдра найти формы путём усечения вершин или рёбер. Для определённости далее она решена для 30 закрытых простых форм (з.п.ф.). При этом эквивалентные (т.е. равного положения, переводимые друг в друга преобразованиями симметрии) вершины и рёбра усекаются одинаково (т. е. секущая плоскость ориентирована одинаково относительно эквивалентных граней, сходящихся в вершине или на ребре).

Легко видеть, что вершинные усечения приводят к геометрически дуальным формам, хорошо известным в минералогии: комбинация призмы и пинакоида дуальна одноименной бипирамиде, октаэдр дуален кубу (рис. 1), и т. д. Уже эти примеры обнаруживают в задаче Роме-де-Лиля реальную (диктуемую природой) подоплёку. Таким образом, эта часть задачи допускает иную, совершенно нетривиальную формулировку: в каждом ли классе симметрии допустима форма, геометрически дуальная исходной з.п.ф.? Для решения задачи составлены оригинальные компьютерные алгоритмы, среди прочего по- 32

зволяющие распознавать вершинные и рёберные усечения, выделяя п.ф.в их сложных комбинациях. Результаты сведены в табл. 1, 2 и рис. 2.

В результате вершинных усечений найдено, что все классы симметрии допускают форму, дуальную к з.п.ф. Соответствующие комбинации п.ф. предлагается выделить как особые. (В классах 23 и -43m кубу дуальна комбинация двух тетраэдров — гемиэдрических форм октаэдра. К сожалению, тема голо-, геми-, тетарто- и ог-доэдрии незаметно исчезла из кристалломорфологии. Некогда она связывала п.ф. в ряды родственных форм. В результате исследования между з.п.ф. обнаружены связи иного рода). В тригональной сингонии ромбоэдр и дит-ригональный скаленоэдр имеют в качестве дуальных различные комбинации ромбоэдра и пинакоида. Для 1-го она выглядит как тригональная антипризма. Для 2-го — она же, срезанная параллельно пинакоиду так, что треугольные грани стали трапециями. В кубической сингонии ромбододекаэдр, тетрагонтритетраэдр, гексатетраэдр, тригонтриоктаэдр и тетрагексаэдр имеют в качестве дуальных форм различные комбинации куба и октаэдра (или двух тетраэдров). Тетрагонтриоктаэдр и гексоктаэдр имеют в качестве дуальных различные комбинации ромбододекаэдра, октаэдра и куба. Отличия между ними состоят в разном развитии п.ф. Одна комбинация получается из другой движениями граней вдоль нормалей. Им соответствуют повороты граней исходных з.п.ф. на рёбрах. Так, грани дитригонального скаленоэдра, попарно сливаясь в параллельном положении, образуют грани ромбоэдра.

Таблица 1. Вершинные усечения з.п.ф. Table 2. CSF vertex truncations

№	Исходная з.п.ф.		Вершинное усечение
Ромбическая сингония
1	Тетраэдр ромб. (4)		Тетраэдр ромб.
2	Бипирамида ромб. (2 + 2 + 2)		3 пинакоида
Тригональная и гексагональная сингонии
3	Бипирамида триг. (3 + 2)		Призма триг. + пинакоид
4	Ромбоэдр (6 + 2)		Ромбоэдр + пинакоид (триг. антипризма)
5	Трапецоэдр триг. (6 + 2)		Трапецоэдр триг. + пинакоид
6	Бипирамида дитриг. (6 + 2)		Призма дитриг. + пинакоид
7	Скаленоэдр дитриг. (6 + 2)		Ромбоэдр + пинакоид (усечённая триг. антипризма, грани — трапеции)
8	Трапецоэдр гекс. (12+2)		Трапецоэдр гекс. + пинакоид
9	Бипирамида гекс. (6 + 2)		Призма гекс. + пинакоид
10	Бипирамида дигекс. (12 + 2)		Призма дигекс. + пинакоид
Тетрагональная сингония
11	Тетраэдр тетр. (4)		Тетраэдр тетр.
12	Бипирамида тетр. (4 + 2)		Призма тетр. + пинакоид
13	Скаленоэдр тетр. (4 + 2)		Тетраэдр тетр. + пинакоид
14	Трапецоэдр тетр. (8 + 2)		Трапецоэдр тетр. + пинакоид
15	Бипирамида дитетр. (8 + 2)		Призма дитетр. + пинакоид
Кубическая сингония
16	Тетраэдр куб. (4)	Тетраэдр куб.
17	Октаэдр (6)	Куб
18	Куб (8)	Октаэдр (m3, 432, m3m) или 2 тетраэдра (23, 43 т)
19	Ромбододекаэдр (8 + 6)	Октаэдр (m3, 432, m3m) или 2 тетраэдра (23, 43 т) (архимедов кубооктаэдр) + куб
20	Пентагондодекаэдр (12 + 8)	Пентагондодекаэдр + октаэдр (m3) или 2 тетраэдра (23) («икосаэдр» на кристаллах пирита)
21	Тригонтритетраэдр (4 + 4)	2 тетраэдра (усечённый тетраэдр)
22	Тетрагонтритетраэдр (6 + 4 + 4)	Куб + 2 тетраэдра (тетраэдр, усечённый по рёбрам и вершинам, грани -тритоны)
23	Пентагонтритетраэдр (12 + 4 + 4)	Пентагонтритетраэдр + 2 тетраэдра
24	Гексатетраэдр (6 + 4 + 4)	Куб + 2 тетраэдра (тетраэдр, усечённый по рёбрам и вершинам, грани -гексагоны)
25	Тригонтриоктаэдр (8 + 6)	Октаэдр + куб (усечённый куб)
26	Тетрагонтриоктаэдр (12 + 8 + 6)	Ромбододекаэдр + октаэдр + куб (грани октаэдра - тригоны, остальные - тетрагоны)
27	Пентагонтриоктаэдр (24 + 8 + 6)	Пентагонтриоктаэдр + октаэдр + куб
28	Тетрагексаэдр (8 + 6)	Октаэдр (432, тЗш) или 2 тетраэдра (43 m) + куб (усечённый октаэдр)
29	Дидодекаэдр (12 + 8 + 6)	Пентагондодекаэдр + октаэдр + куб
30	Гексоктаэдр (12 + 8 + 6)	Ромбододекаэдр + октаэдр + куб (грани ромбододекаэдра - тетрагоны, октаэдра — гексагоны, куба — октагоны)
Примечание: после названия исходной з.п.ф. в скобках — числа эквивалентных вершин.

Note: after name of initial CSF in brackets — numbers of equivalent vertex

Таблица 2. Рёберные усечения з.п.ф. Table 2. CSF rib truncations

№	Исходная з.п.ф.	Рёберное усечение
Ромбическая сингония
1	Тетраэдр ромб. (2 + 2 + 2)	3 пинакоида
2	Бипирамида ромб. (4 + 4 + 4)	3 призмы ромб.
Тригональная и гексагональная сингонии
3	Бипирамида триг. (6 + 3)	Бипирамида триг. + призма триг.
4	Ромбоэдр (6 + 6)	Ромбоэдр + призма гекс.
5	Трапецоэдр триг. (6 + 3 + 3)	Трапецоэдр триг. + 2 призмы триг.
6	Бипирамида дитриг. (6 + 6 + 6)	Призма дитриг. + 2 бипирамиды триг.
7	Скаленоэдр дитриг. (6 + 6 + 6)	2 ромбоэдра + призма гекс.
8	Трапецоэдр гекс. (12 + 6 + 6)	Трапецоэдр гекс.+ 2 призмы гекс.
9	Бипирамида гекс. (12 + 6)	Бипирамида гекс. + призма гекс.
10	Бипирамида дигекс. (12 + 12 + 12)	2 бипирамиды гекс. + призма дигекс.

Окончание таблицы 2

End of table 2

№	Исходная з.п.ф.	Рёберное усечение
Тетрагональная сингония
11	Тетраэдр тетр. (4 + 2)	Призма тетр. + пинакоид
12	Бипирамида тетр. (8 + 4)	Бипирамида тетр. + призма тетр.
13	Скаленоэдр тетр. (4 + 4 + 4)	Призма тетр. + 2 тетраэдра тетр.
14	Трапецоэдр тетр. (8 + 4 + 4)	Трапецоэдр тетр. + 2 призмы тетр.
15	Бипирамида дитетр. (8 + 8 + 8)	Призма дитетр. + 2 бипирамиды тетр.
Кубическая сингония
16	Тетраэдр куб. (б)	Куб
17	Октаэдр (12)	Ромбододекаэдр
18	Куб (12)	Ромбододекаэдр
19	Ромбододекаэдр (24)	Тетрагонтриоктаэдр
20	Пентагондодекаэдр (24 + б)	Дидодекаэдр + куб
21	Тригонтритетраэдр (12 + б)	Тетрагонтритераэдр + куб
22	Тетрагонтритетраэдр (12 + 12)	2 тригонтритетраэдра
23	Пентагонтритетраэдр (12+12 + б)	2 пентагонтритетраэдра + куб
24	Гексатетраэдр (12 + 12 + 12)	2 тригонтритетраэдра + тетрагонтритетраэдр
25	Тригонтриоктаэдр (24 +12)	Тетрагонтриоктаэдр + ромбододекаэдр
26	Тетрагонтриоктаэдр (24 + 24)	Тригонтриоктаэдр + тетрагексаэдр
27	Пентагонтриоктаэдр (24 + 24 + 12)	2 пентагонтриоктаэдра + ромбододекаэдр
28	Тетрагексаэдр (24 +12)	Тетрагонтриоктаэдр + ромбододекаэдр
29	Дидодекаэдр (24 + 12 + 12)	Дидодекаэдр + 2 пентагондодекаэдра
30	Гексоктаэдр (24 + 24 + 24)	Тригонтриоктаэдр + тетрагонтриоктаэдр + тетрагексаэдр

Примечание: после названия исходной з.п.ф. в скобках — числа эквивалентных рёбер. Note: after name of initial CSF in brackets — numbers of equivalent rib

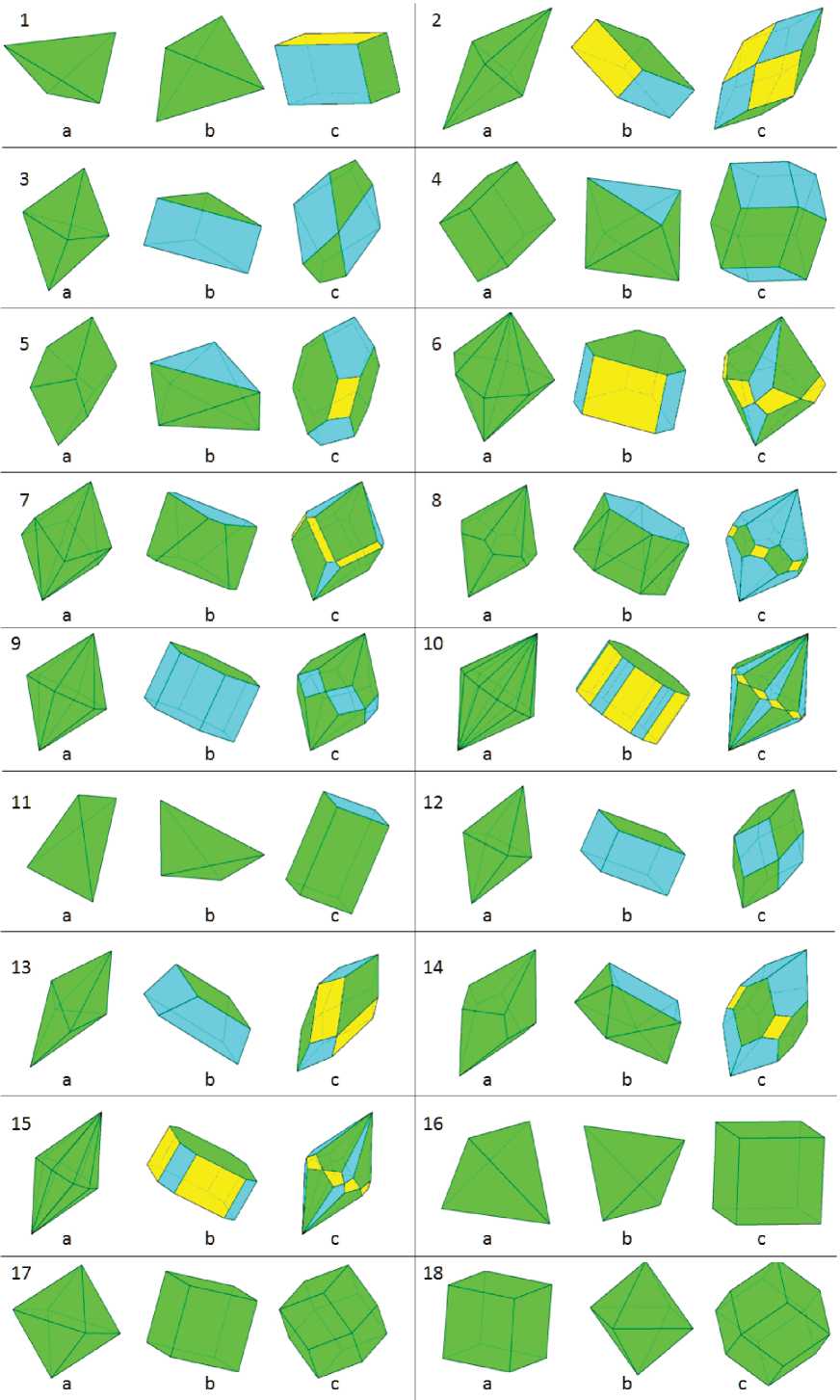
Рис. 2. Усечения з.п.ф. Номера соответствуют табл. 1 и 2, а — исходная з.п.ф., b — вершинное усечение, с — рёберное усечение. Разными цветами даны грани разных п. ф.

Fig. 2. CSF Truncations. The numbers correspond to Table 1 and 2, a - initial CSF, b - vertex truncation, c — rib truncation. Different colors show faces of different forms

Рис. 1. Слева: комбинация ромбической призмы, ромбической бипирамиды и пинакоида на топазе . Справа: комбинация октаэдра и куба на флюорите

Fig. 1. Left: combination of rhombic prism, rhombic bipyramid and pinacoid on topaz . Right: combination of octahedron and cube on fluorite

Результатом рёберных усечений для октаэдра и куба является ромбододекаэдр (из теоремы Эйлера следует, что у геометрически дуальных выпуклых полиэдров числа рёбер совпадают, но всегда ли совпадают их рёберные усечения — вопрос не тривиальный), для тригонтри-октаэдра и тетрагексаэдра — комбинация тетрагонтриок-

таэдра и ромбододекаэдра (в классе -43m тетрагонтриок-таэдр замещён комбинацией двух тригонтритетраэдров — это ещё один пример гемиэдрии). Это подчёркивает родство указанных исходных з.п.ф. Продолжение задачи Роме-де-Лиля состоит в перечислении одновременно вершинных и рёберных усечений всех з.п.ф., а также

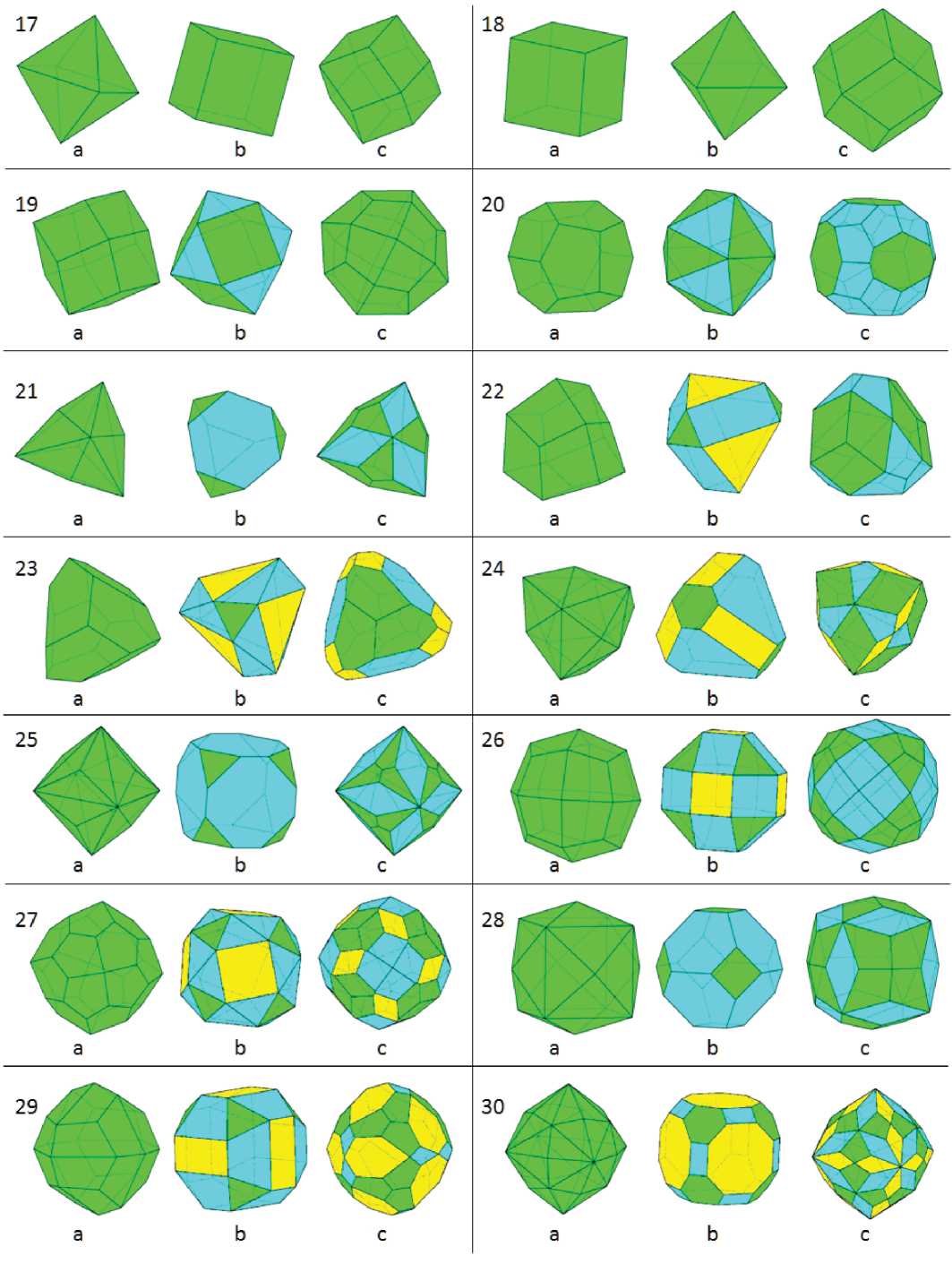
Окончание рис. 2

End of fig. 2

поиске их природных реализаций. Очевидно, теоретическая и практическая кристалломорфология далеко не исчерпала своих ресурсов.

Список литературы Вершинные и рёберные усечения закрытых простых форм: к 280-летию Ж. Б. Л. Роме-де-Лиля и 80-летию Н. П. Юшкина

Шафрановский И.И. Лекции по кристалломорфологии. М.: Высшая школа, 1968. 174 с.
Шафрановский И.И. История кристаллографии с древнейших времён до начала XIX столетия. Л.: Наука, 1978. 297 с.
Юшкин Н.П. История минералогии и эволюция фундаментальных минералогических идей. Препр. 102. Сыктывкар: Ин-т геологии Коми фил. АН СССР, 1984. 52 с.

Статья научная