Вибрации зданий с подвижным фундаментом при реальных сейсмических воздействиях

Автор: Мирзаев Ибрагим, Турдиев Маликжон Сайфиддин Оглы

Журнал: Строительство уникальных зданий и сооружений @unistroy

Статья в выпуске: 1 (94), 2021 года.

Бесплатный доступ

Объектом исследования являлись колебания зданий на скользящих фундаментах с сухим трением под действием реальных землетрясений. Методы. Использованы образцы четырехэтажного и девятиэтажного дома с набором из пяти записей землетрясений по шкале 7-10 баллов по шкале MSK-64. Расчетная модель здания представляет собой систему со многими степенями свободы, подверженную только сдвиговым колебаниям. Кулоновская модель сухого трения описывает взаимодействие фундамента и ростверка. Движение фундамента задается как горизонтальная составляющая сейсмограммы реального землетрясения. Отсутствие условия для расчета силы трения между двумя абсолютно твердыми телами в период их сцепления в динамике не позволяет определить время начала скольжения, что усложняет задачу. Кроме того, сейсмограммы реальных землетрясений имеют сложный характер, что может привести к многократным изменениям состояния скольжения и сцепления ростверка и фундамента. Дискретность задачи по времени и использование логического алгоритма позволили решить эту задачу. Использовалась неявная схема Ньюмарка; на каждом временном шаге задача решалась в трех постановках и выбиралось истинное решение. Для обеспечения необходимой точности решения нелинейной задачи величина временного шага была выбрана путем проведения вычислительного эксперимента. Полученные результаты. Разработанный алгоритм расчета перемещений, скоростей, ускорений и поперечных сил был предложен на основе горизонтальной составляющей записи сейсмограммы. Полученные результаты представлены в виде сравнительных графиков перемещений ростверка и фундамента, а также поперечной силы первого этажа. Результаты также были представлены в десяти таблицах для четырехэтажных и девятиэтажных зданий, подвергшихся влиянию пяти землетрясений. В этих таблицах показаны максимальные значения поперечных сил для перекрытий зданий. При благоприятном сочетании динамических характеристик здания и амплитудно-частотной характеристики сейсмограммы использование скользящего фундамента может привести к многократному снижению поперечной силы в здании, а их плохое сочетание в скользящем фундаменте. дает незначительный эффект. Показано, что скользящий фундамент не всегда приводит к многократному снижению поперечной силы.

Еще

Сейсмические волны, динамика зданий, сейсмическая изоляция, фторопласт, сухое трение

Короткий адрес: https://sciup.org/143175795

IDR: 143175795 | DOI: 10.4123/CUBS.94.7

Текст научной статьи Вибрации зданий с подвижным фундаментом при реальных сейсмических воздействиях

Важность защиты зданий и сооружений от воздействия сильных землетрясений не вызывает сомнений, так как это связано с жизнью и здоровьем людей. Для уменьшения силы воздействия землетрясений на здания и сооружения используются различные способы сейсмоизоляции, демпфирования и другие конструктивные решения [1]–[22].

Для определенных типов зданий эффективным способом сейсмоизоляции является скользящий фундамент с использованием фторопласта [19], [20]. В [23]; описаны результаты обработки замеренных ускорений вовремя землетрясения трех зданий, построенных в г. Алматы, Казахстан, в 1989 году. Эти три здания построены с одинаковой над фундаментной частью (9этажные крупнопанельные дома серии 158), но различными фундаментами: обычными ленточными, кинематическими и опорами с прокладками из фторопласта. При этом контактирующие поверхности с фторопластом имеют наклонные плоскости. 16 августа 2014 г.

было зарегистрировано землетрясение, эпицентр которого был расположен в 41 км на восток от г. Алматы. Подземные толчки ощущались в г. Алматы в 4 – 5 баллов по шкале MSK-64. Максимальные величины спектрального коэффициента β для сейсмоизолируемых зданий в уровне 9-го этажа меньше аналогичной величины для здания-аналога: для зданий с фторопластовыми прокладками - на 11%, для зданий с кинематическим фундаментом - на 63%. В [24]; приведены результаты лабораторного эксперимента на модели здания жесткого типа с сейсмоизолирующим скользящим поясом из стали и фторопласта с коэффициентом трения 0.04, показана возможность снижения ускорения здания до 10 раз для землетрясения интенсивности 10 баллов по шкале MSK-64. По результатам экспериментов на гармоническом воздействии с частотой до 10 Гц и ускорением платформы до 10 м/с² построен график изменения отношения ускорения сооружения к ускорению сейсмического воздействия. В лабораторном эксперименте [14]; на сейсмоплатформе с реализацией реальных сейсмограмм показано, что разные землетрясения на тело с сейсмоизолирующим слоем действуют по-разному. В [15]; рассмотрены вопросы выбора оптимального значения коэффициента сухого трения для снижения воздействия землетрясения на здания со скользящим фундаментом, когда здание моделируется как масса с пружиной, а масса ростверка не учитывается, и решается задача по модели идеального упругопластического взаимодействия. В [8]–[10]; приведены результаты исследований пространственных конструкций зданий на действие реальных землетрясений по комплексу программ LS-DYNA. При изучении движения материальной точки на шероховатой плоскости [11], [25]; предполагается, что на материальную точку всегда действует сила сухого трения, направленная против движения, при этом многократные остановы и скольжения не рассмотрены. В [12]; рассмотрены различные модели взаимодействия основания с телом, отмечена неизвестность силы трения при отсутствии скольжения. В [17]; сейсмоизолирующее устройство моделируется билинейной моделью взаимодействия при исследовании колебания зданий под действием реальных землетрясений, описывается подробный алгоритм решения нелинейной задачи.

В нелинейных задачах сейсмодинамики подземных сооружений используют модель сухого трения при взаимодействии трубопровода с грунтом. В [26]; рассмотрены задачи воздействия волны, распространяющейся в грунте, на прямолинейный трубопровод при его взаимодействии с грунтом по модели упругопластического тела с учетом динамического давления грунта. Решение задач производится методом характеристик. В [27]; предложена оценка сейсмостойкости подземных трубопроводов сложной конфигурации на основе записей реальных землетрясений. Нестационарные задачи для стержня с внешним сухим трением решены методом характеристик в [28]. В [29]; построена конечно-разностная аппроксимация уравнения движения стержня с внешним сухим трением при моделировании задачи выдергивания буровых труб ударным воздействием и разработан алгоритм решения нелинейной задачи, позже этот алгоритм использован в [30]–[32].

В динамических задачах двух абсолютно твердых тел с сухим трением Кулона значение силы трения до начала скольжения является неизвестной величиной, и поэтому в строгой постановке задачи определение начала скольжения становится проблематичной. В опубликованных работах для обхода этой проблемы вводят упругий участок в модель взаимодействия двух тел, либо начало скольжения связывают с значением действующих на тела внешних сил, не учитывая ускорения тел.

В настоящей работе будем использовать алгоритм, описанный в [29]; логический алгоритм определения скольжения и отсутствия относительного движения в динамике, для задач расчета зданий со скользящим фундаментом при действии сейсмических волн реальных землетрясений.

2 Materials and Methods

Пусть задано горизонтальное движение основания здания в виде сейсмограммы реального землетрясения. Будем считать, что нижняя часть фундамента здания приобретает такое же перемещение, а верхняя часть фундамента или ростверк разделен от нижней части фундамента двухслойным фторопластом [19], [20]. В качестве модели взаимодействия двух слоев фторопласта примем модель сухого трения Кулона.

Здание представим одномерной сдвиговой моделью с сосредоточенными массами и безынерционными упругими связами

[ M ] • {U } + [ C ] • { U } + [ K ] • { U } = {Q ( t )}, (1)

{U} = 0, {U} = 0, при t = 0, где [M] - диагональная матрица масс, массы расположены в уровнях этажей, [K] - матрица жесткостей, [C] = а • [M] + в• [K] - матрица вязкости, {U} - вектор перемещений. Условие взаимодействия массы M со скользящим нижним фундаментом имеет вид и0 = Ug — u.-, если |FI < F/r |, т.е. при совместном движении, (2)

F _o = F. , при скольжении, (3)

где u – перемещение ростверка; u – перемещение нижней части фундамента, т.е. аппроксимированная функция оцифрованной сейсмограммы горизонтальной составляющей землетрясения; u – величина сдвига в момент времени в начале текущего совместного движения нижней части фундамента и ростверка, т.е. разность между значениями перемещений нижней части фундамента и ростверка (в начальный момент времени и_г = 0 ); F _o - неизвестное значение силы сцепления между верхним и нижним фундаментами; F^ = sign(U_g - U _o) • f • P - значение силы сухого трения; f – коэффициент сухого трения; P – вес здания.

При совместном движении перемещение u определяется по равенству (2) и уравнение движения массы M имеет вид

M₁u ₁ + ku + cu - k ₂ ( u ₂ - u_x ) - c ₂ ( U ₂ - U ]) = ku + c_xU₀ .

В этом случае Q = ku + c_xU₀ , остальные элементы вектора { Q } равны нулю.

Скольжение с сухим трением наступает только тогда, когда выполняется условие (3). Рассматриваемая задача (1), (2), (3) является нелинейной задачей, при этом отсутствуют условия вычисления неизвестной функции F , далее покажем отсутствие необходимости вычисления значения этой функции. Скольжение может произойти только тогда, когда ростверк набрал необходимую силу инерции, а ускорение фундамента в этот момент снижается. Поэтому при слабых землетрясениях скользящий фундамент не срабатывает или эффект будет небольшим [23]. Во время динамического процесса изменяются размерности матриц [ M ] и [ K ] . При скольжении имеет место уравнение для массы M

M ₀ • и о - k_x(u_x - u ₀) - c_X(U_X - U ₀) = F r , при этом Q₀ = F_fr .

Для решения задачи в целом воспользуемся следующим алгоритмом. На каждом шаге по времени решаем задачи в трех постановках:

1. уравнение (1) решаем с условием (2);
2. уравнение (1) решаем с условием (3), при этом F = f • P ;
3. уравнение (1) решаем с условием (3), при этом F _o =- f • P .

Матрицы [ M ] и [ K ] в первой постановке имеют размер m х m (здесь m - количество этажей здания), а во второй и третьей постановках ( m + X) х ( m + X). Выбор истинного решения из этих трех решений осуществляется следующим образом. Если относительные скорости U_g - U _o во втором и третьем постановках задач имеют разные знаки, тогда истинным решением является решение задачи в первой постановке, потому что приложенная сила сухого трения заставляет двигаться ростверк в разные стороны и значит неизвестная сила меньше предельного значения силы сухого трения, т.е. отсутствует скольжение. Если относительные скорости во второй и третьей постановках задач имеют одинаковый знак, тогда истинным решением является решение задачи в той постановке, в которой относительная скорость по абсолютному значению наименьший, потому что сила сухого трения направлена против относительного движения и всегда приводит затуханию относительного движения. Все три задачи решаются методом Mirzaev, I.; Turdiyev, M. S.

Ньюмарка [1]; оцифрованная сейсмограмма землетрясения аппроксимируется линейной функцией в интервале шага записи, когда шаг аппроксимации по времени меньше шага записи землетрясения.

3 Results and Discussion

Обсудим результаты расчетов на следующих примерах. Пусть заданы характеристики 4 и 9 этажных зданий, а также сейсмограммы следующих землетрясений [33]:

1. Forgaria-Cornio – 000114 (11.09.1976 г, 7 баллов по MSK-64, максимальное ускорение – 1.05 м/с², максимальное перемещение – 0.0016 м, шаг оцифрования – 0.005 с, продолжительность – 18.085 с);
2. Cairano 3 – 000319 (16.01.1981 г, 8 баллов по MSK-64, максимальное ускорение – 1.47 м/с², максимальное перемещение – 0.0029 м, шаг оцифрования – 0.005 с,
3. Tolmezzo-Diga Ambiesta – 000055 (06.05.1976 г, 9 баллов по MSK-64, максимальное ускорение – 3.35 м/с², максимальное перемещение – 0.0039 м, шаг оцифрования – 0.005 с, продолжительность – 46.535 с);
4. Nocera Umbra 2 – 000856 (03.04.1998 г, 9 баллов по MSK-64, максимальное ускорение – 3.73 м/с², максимальное перемещение – 0.0054 м, шаг оцифрования – 0.005 с,
5. Nocera Umbra – 000593 (26.09.1997 г, 10 баллов по MSK-64, максимальное ускорение – 5.1 м/с², максимальное перемещение – 0.0133 м, шаг оцифрования – 0.005 с, продолжительность – 33.170 с).

продолжительность – 22.175 с);

продолжительность – 40.990 с);

Четырехэтажное здание серии 76-017СА/53 имеет следующие характеристики: кирпичное здание размером в плане 389.88 м ² ; сосредоточенные массы в уровнях верхней части фундамента и этажей М_о = 497575 кг , М_х = 495000 кг , М_г = 495000 кг , М₃ = 495000 кг , М₄ = 698000 кг , при этом общий вес здания, давящий на нижнюю часть фундамента, равен P = 26269635 Н ; сдвиговые жесткости по этажам одинаковы k = 16.08 - 10 8 Н/м; вязкость материала здания по этажам одинаковы ц_х = 26.9-10⁵ Нс/м.

Девятиэтажное здание серии 76-017СП/53 имеет следующие характеристики: крупнопанельное здание размером в плане 291.6 м ² ; сосредоточенные массы в уровнях верхней части фундамента и этажей М _о = 449000 кг , М_х = 379500 кг , М₂ = 379500 кг , М₃ = 379500 кг , М₄ = 379500 кг, М₅ = 379500 кг , М ₆ = 379500 кг , М₇ = 379500 кг , М ₈ = 379500 кг ,

М = 341000 кг , при этом общий вес здания, давящий на нижнюю часть фундамента, равен P = 37494800 Н ; сдвиговые жесткости по этажам одинаковы k = 32.357 - 10⁹ Н/м; вязкость материала здания по этажам одинаковы ^ = 10.581 0⁶ Нс/м.

При численном решении задач с сухим трением, не зависимо от выбора явной или неявной конечно-разностной схемы, шаг по времени необходимо подбирать для обеспечения достаточной точности. В наших примерах расчетов шаг по времени был выбран равным 0.0001 с.

Ниже, при анализе рисунков и в таблицах, использованный процент снижения максимального значения сдвигового усилия 0 вычислялся по формуле

О =

q max| q 1max

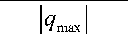
- 100%

где q – максимальное значение сдвигового усилия без учета скольжения, q1max максимальное значение сдвигового усилия с учетом скольжения.

На рис. 1 представлены результаты расчетов изменения перемещений по времени верхней и нижней частей фундамента четырехэтажного здания при землетрясении №4. Время начала скольжения от начала процесса воздействия сейсмической волны равно 13.45 с. Возникновение первого скольжения связано с изменением направления движения нижнего фундамента. Далее Mirzaev, I.; Turdiyev, M. S.

Vibrations of Buildings with Sliding Foundations under Real Seismic Effects;

происходит смена перехода от скольжения с сухим трением к совместному движению и обратно много раз, в зависимости от рассмотренных выше условий. К концу процесса остаточный сдвиг равно 0.009 м.

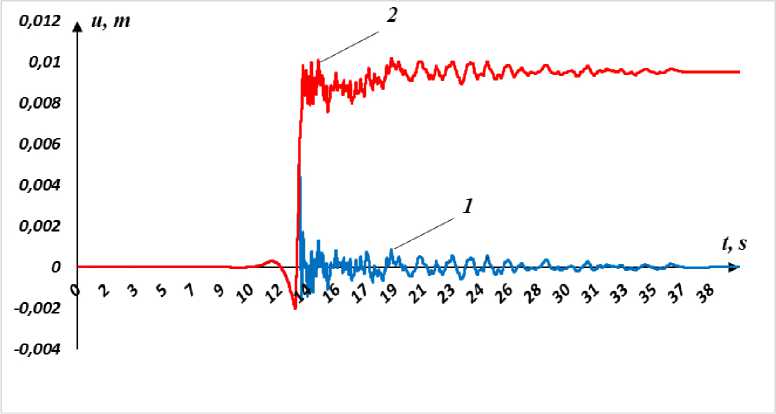
Рис. 1 - Перемещения нижней (1) и верхней (2) частей фундамента по времени четырехэтажного здания

Fig. 1 - Displacement of the lower (1) and upper (2) parts of the foundation over time of the four-story building

На рис. 2 представлены результаты расчетов изменения перемещений по времени верхней и нижней частей фундамента девятиэтажного здания при землетрясении №4. Время начала скольжения от начала процесса воздействия сейсмической волны равно 13.45 с. Далее происходит смена перехода от скольжения с сухим трением к совместному движению и обратно много раз, в зависимости от рассмотренных выше условий. После 19-ой секунды процесса движение верхней части фундамента приблизительно повторяет форму движения нижней части фундамента, хотя в очень маленьких промежутках времени происходит скольжение. К концу процесса остаточный сдвиг равно 0.0064 м. Следует отметить, что в случае девятиэтажного здания остаточный сдвиг меньше, что связано с отличием процессов колебаний зданий разной этажности.

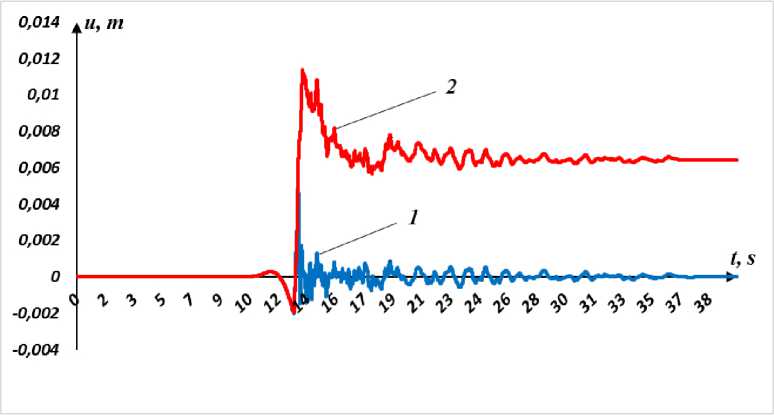
Рис. 2 - Перемещения нижней (1) и верхней (2) частей фундамента по времени девятиэтажного здания

Fig. 2 - Displacement of the lower (1) and upper (2) parts of the foundation over time of the nine-story building

На рис. 3 представлены результаты расчетов изменения сдвиговых усилий по времени в первом этаже четырехэтажного здания при землетрясении №4 для случаев без учета и с учетом скользящего элемента. Из этих графиков видно, что использование скользящего фундамента с фторопластом с коэффициентом сухого трения f = 0.05 приводит к снижению максимального значения сдвигового усилия на 69% (т.е. в 3.2 раза) по отношению к случаю отсутствия скользящего фундамента. Во второй половине процесса из–за уменьшения ускорений в сейсмической волне разница между максимальными значениями сдвиговых усилий уменьшается.

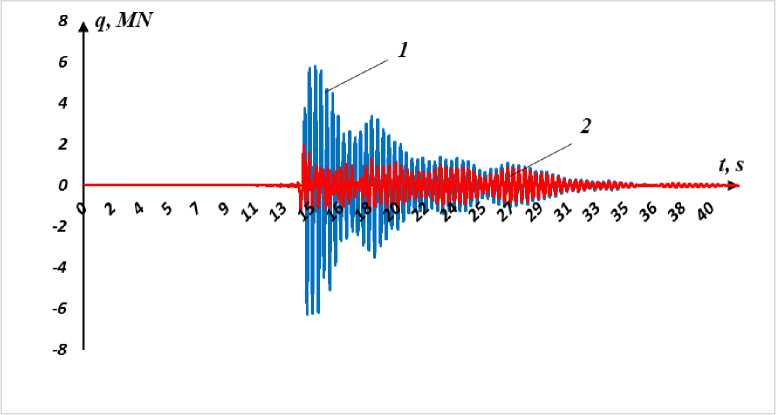
Рис. 3 - Изменение сдвиговой силы на первом этаже четырехэтажного здания без учета скольжения (1) и с учетом скольжения (2)

Fig. 3 - Change in the shear force on the first floor of the four-story building without regard to sliding (1) and with regard to sliding (2)

На рис. 4 представлены результаты расчетов изменения сдвиговых усилий по времени в первом этаже девятиэтажного здания при землетрясении №4 для случаев без учета и с учетом скользящего элемента. Из этих графиков видно, что использование скользящего фундамента с фторопластом с коэффициентом сухого трения f = 0.05 приводит к снижению максимального значения сдвигового усилия на 74% (т.е. в 3.8 раза) по отношению к случаю отсутствия скользящего фундамента. Во второй половине процесса из–за уменьшения ускорений в сейсмической волне разница между максимальными значениями сдвиговых усилий уменьшается.

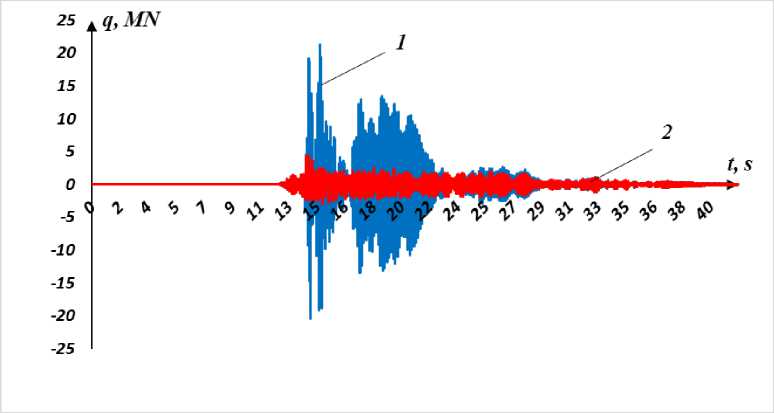
Рис. 4 - Изменение сдвиговой силы на первом этаже девятиэтажного здания без учета скольжения (1) и с учетом скольжения (2)

Fig. 4 - Change in the shear force on the first floor of the nine-story building without regard to sliding (1) and with regard to sliding (2)

На рис. 5 представлены результаты расчетов изменения перемещений по времени верхней и нижней частей фундамента четырехэтажного здания при землетрясении №3. Время начала скольжения от начала процесса воздействия сейсмической волны равно 8.55 с. Далее происходит смена перехода от скольжения с сухим трением к совместному движению и обратно много раз, в зависимости от рассмотренных выше условий. К концу процесса остаточный сдвиг равно 0.0196 Mirzaev, I.; Turdiyev, M. S.

м. Сравнение рис. 1 и рис. 5 показывает, что сейсмическая волна землетрясения №3 имеет меньшую доминантную частоту по сравнению с землетрясением №4. Спектральные кривые используемых записей землетрясений приведены в [33].

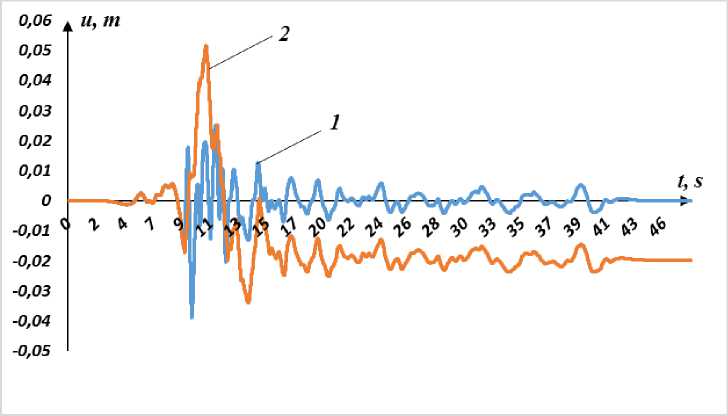
Рис. 5 - Перемещения нижней (1) и верхней (2) частей фундамента по времени четырехэтажного здания

Fig. 5 - Displacement of the lower (1) and upper (2) parts of the foundation over time of the four-story building

На рис. 6 представлены результаты расчетов изменения перемещений по времени верхней и нижней частей фундамента девятиэтажного здания при землетрясении № 3. Время начала скольжения от начала процесса воздействия сейсмической волны равно 8.12 с. Далее происходит смена перехода от скольжения с сухим трением к совместному движению и обратно много раз, в зависимости от рассмотренных выше условий. К концу процесса остаточный сдвиг равно 0.0689 м.

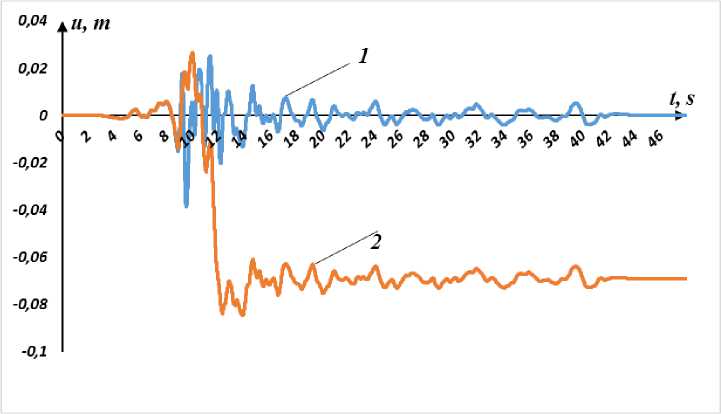
Рис. 6 - Перемещения нижней (1) и верхней (2) частей фундамента по времени девятиэтажного здания

Fig. 6 - Displacement of the lower (1) and upper (2) parts of the foundation over time of the nine-story building

На рис. 7 представлены результаты расчетов изменения сдвиговых усилий по времени в первом этаже четырехэтажного здания при землетрясении №3 для случаев без учета и с учетом скользящего элемента. Из этих графиков видно, что использование скользящего фундамента с фторопластом с коэффициентом сухого трения f = 0.05 приводит к снижению максимального значения сдвигового усилия на 89% (т.е. в 8.9 раза) по отношению к случаю отсутствия скользящего фундамента. Этот результат согласуется с результатом лабораторного эксперимента для здания жесткого типа [24]. Во второй половине процесса из–за уменьшения Mirzaev, I.; Turdiyev, M. S.

Vibrations of Buildings with Sliding Foundations under Real Seismic Effects;

ускорений в сейсмической волне разница между максимальными значениями сдвиговых усилий уменьшается.

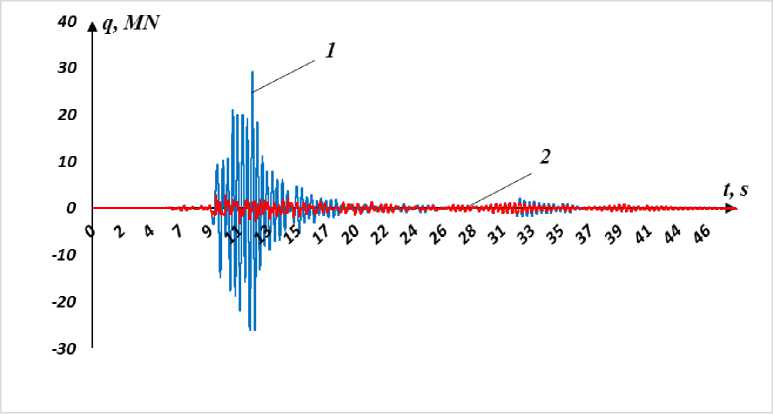
Рис. 7 - Изменение сдвиговой силы на первом этаже четырехэтажного здания без учета скольжения (1) и с учетом скольжения (2)

Fig. 7 - Change in the shear force on the first floor of the four-story building without regard to sliding (1) and with regard to sliding (2)

На рис. 8 представлены результаты расчетов изменения сдвиговых усилий по времени в первом этаже девятиэтажного здания при землетрясении №3 для случаев без учета и с учетом скользящего элемента. Из этих графиков видно, что использование скользящего фундамента с фторопластом с коэффициентом сухого трения f = 0.05 приводит к снижению максимального значения сдвигового усилия всего на 10% (т.е. в 1.1 раза) по отношению к случаю отсутствия скользящего фундамента.

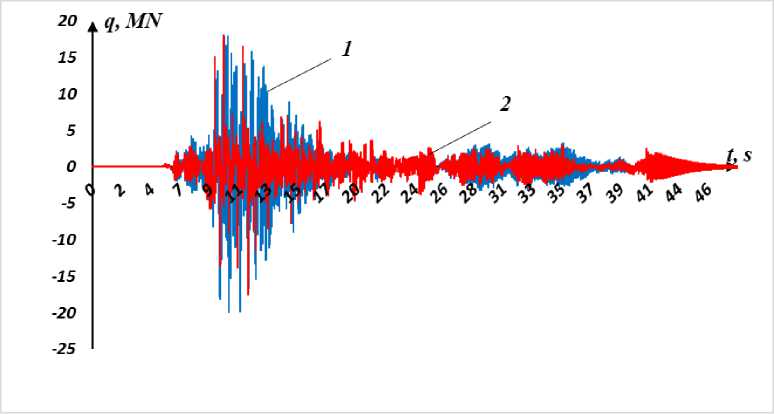
Рис. 8 - Изменение сдвиговой силы на первом этаже девятиэтажного здания без учета скольжения (1) и с учетом скольжения (2)

Fig. 8 - Change in the shear force on the first floor of the nine-story building without regard to sliding (1) and with regard to sliding (2)

Во второй половине процесса из–за уменьшения ускорений в сейсмической волне разница между максимальными значениями сдвиговых усилий уменьшается. Далее в таблицах также будет показано, что скользящий фундамент не всегда приводит к снижению сдвиговых усилий в несколько раз. Все зависит от характеристик здания и характера сейсмической волны. Поэтому, исходя от площадки строительства, необходимо подбирать близкие по преобладающим частотам записи сейсмограмм, и проводить вычисления.

Ниже, в таблицах 1 – 10, приведены максимальные значения сдвиговых усилий по этажам для четырехэтажного и девятиэтажного зданий для различных значений коэффициента сухого Mirzaev, I.; Turdiyev, M. S.

Vibrations of Buildings with Sliding Foundations under Real Seismic Effects;

трения. При использовании скользящего фундамента максимальные значения сдвиговых усилий на верхних этажах здания могут быть, даже несколько раз, больше соответствующих максимальных значений сдвиговых усилий для здания без скользящего фундамента. Увеличение значения коэффициента сухого трения скользящего трения приводит к снижению эффекта от применения скользящего фундамента. Уменьшение массы ростверка может привести к повышению эффективности скользящего фундамента, что наблюдалось для девятиэтажного здания при землетрясении №3. В каждом варианте проекта необходимо проводить соответствующие расчеты. В таблицах 1 – 10 максимальные значения сдвиговых усилий q и q _lmax заданы в килоньютонах, а 9 в процентах.

Таблица 1. Максимальные значения сдвиговых усилий по этажам для девятиэтажного здания при действии землетрясения № 1

Table 1. Maximum values of shear forces by floors for the nine-story building under the action of the earthquake № 1

S го н О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
S го н О	^q max	q 1max	9	q 1max	9	q 1max	9	q 1max	9	q 1max	9	q 1max	9
1	13000	3840	70	4580	65	5490	58	6700	48	8350	36	10000	23
2	12400	3700	70	4490	64	5510	56	6530	47	8320	33	10100	19
3	11700	3810	67	4830	59	5460	53	6690	43	8190	30	9890	15
4	10700	4040	62	4480	58	5040	53	6490	39	7790	27	9300	13
5	9460	3990	58	3920	59	5160	45	5900	38	7060	25	8320	12
6	7870	3830	51	3480	56	5210	34	5020	36	6000	24	6980	11
7	6060	3440	43	3900	36	4310	29	3950	35	4640	23	5340	12
8	4060	2500	38	3210	21	2900	29	2700	33	3100	24	3640	10
9	1950	1340	31	1670	14	1540	21	1510	23	1500	23	1790	8

Таблица 2. Максимальные значения сдвиговых усилий по этажам для четырехэтажного здания при действии землетрясения № 1

Table 2. Maximum values of shear forces by floors for the four-story building under the action of the earthquake № 1

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	9	q 1max	9	q 1max	9	q 1max	9	q 1max	9	q 1max	9
1	3560	1480	58	1810	49	2280	36	3250	9	3560	0	3560	0
2	3210	1470	54	1860	42	2190	32	3130	2	3210	0	3210	0
3	2560	1470	43	1680	34	1940	24	2560	0	2560	0	2560	0
4	1630	1100	33	1230	25	1320	19	1630	0	1630	0	1630	0

Таблица 3. Максимальные значения сдвиговых усилий по этажам для четырехэтажного здания при действии землетрясения № 2

Table 3. Maximum values of shear forces by floors for the four-story building under the action of the earthquake № 2

s го н О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s го н О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	4160	1550	63	2050	51	2660	36	3480	16	4160	0	4160	0
2	3640	1620	55	2110	42	2780	24	3350	8	3640	0	3640	0
3	3070	1700	45	2320	24	2490	19	2750	10	3070	0	3070	0
4	2080	1530	26	1750	16	1660	20	1950	6	2080	0	2080	0

Таблица 4. Максимальные значения сдвиговых усилий по этажам для девятиэтажного здания при действии землетрясения № 2

Table 4. Maximum values of shear forces by floors for the nine-story building under the action of the earthquake № 2

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	24600	3850	84	5360	78	6000	76	7790	68	9460	62	11000	55
2	23700	4300	82	5380	77	6050	74	7820	67	9460	60	10800	54
3	22200	4880	78	5930	73	6260	72	7850	65	9320	58	10700	52
4	20100	4730	76	5730	71	6460	68	7930	61	9300	54	10500	48
5	17500	4610	74	5800	67	6310	64	7830	55	9270	47	10700	39
6	14500	4270	71	5400	63	5780	60	7370	49	8910	39	10200	30
7	11100	4180	62	4640	58	5040	55	6200	44	7490	33	8250	26
8	7420	3230	56	3490	53	3990	46	4390	41	5150	31	5460	27
9	3550	1690	52	1990	44	2220	37	2210	38	2520	29	2610	26

Таблица 5. Максимальные значения сдвиговых усилий по этажам для четырехэтажного здания при действии землетрясения № 3

Table 5. Maximum values of shear forces by floors for the four-story building under the action of the earthquake № 3

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	29200	3270	89	4070	86	4890	83	7280	75	9750	67	10700	63
2	25600	2760	89	4110	84	5070	80	6160	76	9260	64	10500	59
3	19700	2860	85	4130	79	4550	77	5920	70	7980	59	8650	66
4	12100	3020	75	3540	71	4050	67	5460	55	6620	45	6620	45

Таблица 6. Максимальные значения сдвиговых усилий по этажам для девятиэтажного здания при действии землетрясения № 3

Table 6. Maximum values of shear forces by floors for the nine-story building under the action of the earthquake № 3

s го н О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s го н О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	19900	18000	10	28200	-42	33500	-68	33500	-68	32800	-65	33200	-67
2	18600	15600	16	18100	3	28600	-54	32900	-77	23200	-25	25400	-37
3	17200	14800	14	17000	1	24100	-40	29200	-70	19300	-12	23400	-36
4	15300	14200	7	14700	4	19800	-29	25700	-68	17100	-12	23200	-52
5	13200	14000	-6	15700	-19	21000	-60	26200	-98	17700	-34	23700	-80
6	10800	13000	-20	14500	-34	21000	-94	25700	-138	18600	-72	20800	-93
7	8280	12100	-46	13700	-65	19400	-134	23300	-181	21100	-154	22000	-166
8	5510	11000	-99	12000	- 117	15100	-174	18000	-226	23100	-319	22500	-308
9	2640	7310	-177	9890	-274	11400	-332	12900	-388	15700	-494	13800	-422

Таблица 7. Максимальные значения сдвиговых усилий по этажам для четырехэтажного здания при действии землетрясения № 4

Table 7. Maximum values of shear forces by floors for the four-story building under the action of the earthquake № 4

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	6260	1940	69	2100	66	2680	57	4290	31	5110	18	5720	9
2	6070	1460	76	1930	68	2820	54	4560	25	5290	13	5790	5
3	5210	1500	71	2110	60	2850	45	4330	17	4770	8	5030	3
4	3580	1290	64	1720	52	2270	37	3080	14	3200	11	3470	3

Таблица 8. Максимальные значения сдвиговых усилий по этажам для девятиэтажного здания при действии землетрясения № 4

Table 8. Maximum values of shear forces by floors for the nine-story building under the action of the earthquake № 4

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	20400	5350	74	6710	67	8590	58	10900	47	12700	38	14400	29
2	19800	4880	75	5610	72	8990	55	12400	37	12700	36	13500	32
3	18800	4590	76	5430	71	7470	60	11900	37	11900	37	14400	23
4	17400	4440	74	5520	68	7940	54	11800	32	13300	24	12200	30
5	15300	4550	70	5720	63	8310	46	11000	28	13500	12	12700	17
6	12800	4980	61	6230	51	8340	35	10400	19	13100	-2	12500	2
7	9900	4420	55	6200	37	8000	19	9450	5	11800	-19	11600	-17
8	6650	3820	43	5200	22	6890	-4	8420	-26	9400	-41	9450	-42
9	3190	2340	27	2950	8	4010	-26	5130	-61	5120	-61	5180	-62

Таблица 9. Максимальные значения сдвиговых усилий по этажам для четырехэтажного здания при действии землетрясения № 5

Table 9. Maximum values of shear forces by floors for the four-story building under the action of the earthquake № 5

s 5€ го н О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s 5€ го н О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	5130	1970	62	2730	47	2960	42	3920	24	4580	11	5130	0
2	5150	2210	57	2650	49	3160	39	4210	18	5010	3	5150	0
3	4730	2420	49	3020	36	3320	30	4480	5	4560	4	4730	0
4	3480	1950	44	2470	29	2770	20	3650	-5	3340	4	3480	0

Таблица 10. Максимальные значения сдвиговых усилий по этажам для девятиэтажного здания при действии землетрясения № 5

Table 10. Maximum values of shear forces by floors for the nine-story building under the action of the earthquake № 5

s ro H О	Без скольжения	f = 0.05		f = 0.075		f = 0.1		f = 0.15		f = 0.2		f = 0.25
s ro H О	^q max	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0	q 1max	0
1	22300	6600	70	7250	67	8280	63	10400	53	12600	43	15000	33
2	20900	5610	73	7120	66	8980	57	11900	43	13900	33	15800	24
3	19100	6860	64	8150	57	9310	51	10700	44	12100	37	15400	19
4	17000	7050	59	8010	53	10100	41	10900	36	12000	29	13500	21
5	14400	6110	58	8010	45	10100	30	10500	27	11700	19	11800	18
6	11600	5430	53	7750	33	9900	15	10700	8	11600	0	10000	14
7	8780	5040	43	7390	16	8950	-2	10500	-20	10900	-24	9350	-6
8	5900	5120	13	6230	-6	7140	-21	8920	-51	9380	-59	7310	-24
9	2850	3480	-22	3860	-35	4350	-53	5050	-77	5480	-92	4210	-48

4 Conclusions

Приведен алгоритм численного решения задачи колебания зданий со скользящим фундаментом по модели сухого трения Кулона с учетом остановок скольжения. На примере четырехэтажного и девятиэтажного зданий при наборе пяти записей землетрясений показано, что использование скользящего фундамента не всегда приводит к многократному снижению сдвигового усилия. При использовании скользящего фундамента для снижения действия землетрясения необходимо, исходя от площадки строительства, подбирать близкие по преобладающим частотам записи сейсмограмм и проводить вычисления по описанному алгоритму.

Список литературы Вибрации зданий с подвижным фундаментом при реальных сейсмических воздействиях

Chopra, K.A. Dynamics of structures. Fourth Edi . USA, Berkeley, Prentice Hall, One Lake Street, Upper Saddle River, NJ 07458, 2012. 980 p. ISBN:0-13-855214-2. URL: http://faculty.tafreshu.ac.ir/file/download/course/1587566331-dynamic.of.structures.chopra.4thwww.ucivil.ir.pdf.
Tarasov, V.A., Baranovskii, M.Y., Redkin A.V., Sokolov, E.A., Stepanov, A.S. Seismic isolation systems. Construction of Unique Buildings and Structures. 2016. 4(43). Pp. 117–140. URL: https://readera.org/sistemy-sejsmoizoljacii-14322325.
Yuvmitov, A.S., Hakimov, S.R. Study of the seismic isolation influence on the dynamic characteristics of building. ACTA TTPU 2. 2020. Pp. 59–65. URL: https://uzjournals.edu.uz/cgi/viewcontent.cgi?article=1141&context=actattpu.
Iurian, C., Ikhouane, F., Rodellar, J., Robert, G. Identification of a system with dry fiction. Reports de recerca de l’Institut d’Organització i Control de Sistemes Industrials. 2005. URL: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.603.5021&rep=rep1&type=pdf.
Pelekis, I., Madabhushi, G.S.P., DeJong, M.J. Seismic performance of buildings with structural and foundation rocking in centrifuge testing. Earthquake Engineering and Structural Dynamics. 2018. 47(12). Pp. 2390-2409. DOI:10.1002/eqe.3089. URL: https://www.researchgate.net/publication/326511048_Seismic_performance_of_buildings_with_structural_and_foundation_rocking_in_centrifuge_testing.
Vyscrebentseva, M., Le, Q.V. Methods of seismic and seismic isolation using special devices. Don’s Engineering Gazette. 2019. 1. Pp. 2017-2019. URL: https://cyberleninka.ru/article/n/metody-seysmogasheniya-i-seysmoizolyatsii-s-primeneniem-spetsialnyh-ustroystv.
Belash, T. Dry friction dampers in quake-proof structures of buildings. Procedia Engineering. 2015. 117(1). Pp. 397-403. DOI:10.1016/j.proeng.2015.08.184. URL: https://www.researchgate.net/publication/282831750_Dry_Friction_Dampers_in_Quake-proof_Structures_of_Buildings.
Mkrtychev, O.V., Mingazova, S.M. Study of the seismic isolation sliding belt: The case of a monolithic reinforced concrete building. Journal of Physics: Conference Series. 2020. 1425(1). Pp. 3-10. DOI:10.1088/1742-6596/1425/1/012161. URL: https://www.researchgate.net/publication/338445065_Study_of_the_seismic_isolation_sliding_belt_the_case_of_a_monolithic_reinforced_concrete_building.
Mkrtychev, O.V., Mingazova, S.M. Analysis of the reaction of reinforced concrete buildings with a varying number of stories with a seismic isolation sliding belt to an earthquake. IOP Conference Series: Materials Science and Engineering. 2020. 869(5). Pp. 3-12. DOI:10.1088/1757-899X/869/5/052065. URL: https://www.researchgate.net/publication/342850247_Analysis_of_the_reaction_of_reinforced_concrete_buildings_with_a_varying_number_of_stories_with_a_seismic_isolation_sliding_belt_to_an_earthquake.
Mkrtychev, O.V., Bunov, A.A. Calculation on displacements features of seismic isolated building. Vestnik MGSU. 2014. (6). Pp. 63-70. DOI:10.22227/1997-0935.2014.6.63-70. URL: http://vestnikmgsu.ru/ru/component/sjarchive/issue/article.display/2014/6/63-70.
Şcheaua, F.D. Mechanical Systems based on Dry Friction Force used for Building Isolation against Seismic Actions. ANUL XXIV. 2017. (1). Pp. 396–401. URL: http://anale-ing.uem.ro/2017/45.pdf.
Von Kluge, P.N., Germaine, D. K., Crépin, K.T. Dry Friction with Various Frictions Laws: From Wave Modulated Orbit to Stick-Slip Modulated. Modern Mechanical Engineering. 2015. 05(02). Pp. 28-40. DOI:10.4236/mme.2015.52004. URL: http://www.scirp.org/journal/mme.
Buckle, I., Constantinou, M., Dicleli, M., Ghasemi, H. Seismic Isolation of Highway Bridges. University at Buffalo, The State University of New York, 2016. 194 p. ISBN: 9781626239777. URL: https://www.eng.buffalo.edu/mceer-reports/06/06-SP07.pdf.
Banović, I., Radnić, J., Grgić, N. Geotechnical seismic isolation system based on sliding mechanism using stone pebble layer: Shake-table experiments. Shock and Vibration. 2019. 2019. DOI:10.1155/2019/9346232. URL: https://www.hindawi.com/journals/sv/2019/9346232.
Uzdin, A.M., Sandovich, T.A., Amin, Al Naser M.S. Fundamentals of Earthquake-Resistance Theory and Earthquake-Proof Construction of Buildings and Structures. Saint - Petersburg, VNIIG, 1993. 176 p. URL: http://science.totalarch.com/book/1609.rar.
Arutunyan, A.R. Modern methods of seismic insulation of buildings and structures. Engineering and construction journal. 2010. 3(13). Pp. 56–60. DOI: 10.18720/MCE.13.1. URL: https://engstroy.spbstu.ru/userfiles/files/2010/3(13)/arutyunyan_seismoisolation.pdf.
Rashidov, T.R., Kuznetsov, S. V., Mardonov, B.M., Mirzaev, I. Applied problems of seismic dynamics of structures. Book 1. the effect of seismic waves on the underground pipeline and foundations of structures interacting with the ground environment. Tashkent, Navro’z, 2019. 269 p. ISBN:978 9943 565 56 2. URL: http://eqworld.ipmnet.ru/ru/library/books/RashidovKuznetsovMardonovMirzaev2019ru.pdf.
Ajzenberg, Y.M. Seismic isolating adaptive foundation systems. Osnovaniya, Fundamenty i Mekhanika Gruntov. 1992. 29. Pp. 197-202. DOI:10.1007/BF02125532. URL: https://link.springer.com/article/10.1007/BF02125532.
Kuznetsov, V., Chen, S. Sliding girt with fluoroplastic for earthquake-proof building. Engineering and construction journal. 2011. 21(3). Pp. 53–58. DOI:10.18720/MCE.21.8. URL: https://engstroy.spbstu.ru/article/2011.21.7.
Chen, S. Seismically isolated building with sliding fluoroplastic belt. Saint Petersburg, 2011. 86 p. URL: https://scadhelp.com/content/downloads/files/2011/Chehn-mag-2011.pdf.
Sanjaya, K. P., Ravi, S.S. Influence of friction models on response evaluation of buildings with sliding isolation devices. 13th World Conference on Earthquake Engineering. 2004. (1373). URL: https://www.iitk.ac.in/nicee/wcee/article/13_1373.pdf.
Bakre, S. V., Jangid, R. S., Reddy, G.R. Seismic response of piping systems with isolation devices. 13th World Conference on Earthquake Engineering. 2004. (2676). URL: https://www.iitk.ac.in/nicee/wcee/article/13_2676.pdf.
Lapin, V.A., Erjanov, S.E., Daugavet, V.P. Comparative analysis of the effect of seismic isolation using instrumental records of seismic engineering stations. Problems of Mechanics. 2018. (4). Pp. 14–18. DOI:10.6084/m9.figshare.14247425. URL: https://zv17.twirpx.net/3413/3413787_2DE1072E/va_lapin_se_erzhanov_vp_daugavet_comparative_analysis_of_the.pdf.
Apsemetov, M.Ch., Andashev, A.J. Calculation of buildings and structures with seismic-insulating sliding belt for seismic effects with intensity over 9 points. Vestnik MIU. 2017. 3(145). Pp. 86–91. URL: https://www.elibrary.ru/item.asp?id=30671944.
Elmer, F.J. Nonlinear dynamics of dry friction. Journal of Physics A: Mathematical and General. 1997. 30(97).Pp. 6057–6063. DOI:10.1088/0305-4470/30/17/015. URL: https://iopscience.iop.org/article/10.1088/0305-4470/30/17/015.
Sultanov, K.S., Vatin, N.I. Wave Theory of Seismic Resistance of Underground Pipelines. Applied Sciences. 2021. 11(4). Pp. 1797 DOI:10.3390/app11041797. URL: https://www.mdpi.com/2076-3417/11/4/1797.
Bekmirzaev, D.A., Mirzaev, I. Earthquake Resistance Assessment of Buried Pipelines of Complex Configuration Based on Records of Real Earthquakes. Soil Mechanics and Foundation Engineering. 2021. 57(6). Pp. 491–496. DOI:10.1007/s11204-021-09697-0. URL: https://link.springer.com/content/pdf/10.1007/s11204-021-09697-0.pdf.
Nikitin, L. V. Multiple impacts of a bar with external dry friction. Dynamics of Vibro-Impact Systems. 1999. Pp. 221–230. DOI: 10.1007/978-3-642-60114-9_25. URL: https://link.springer.com/chapter/10.1007/978-3-642-60114-9_25.
Mirzaev, I. Dynamics of prestressed rod under impact load. Dynamics Problems of Inelastic Medium: Continuum Dynamics. 1985. 71. Pp. 65–74. URL: https://zv17.twirpx.net/3405/3405370_FD7EC652/dinamika_predvaritelno_napriazhennogo_sterzhnia_pri_deistvii.pdf.
Isakov, A.L., Shmelev, V.V. Wave processes when driving metal pipes into the ground using shock-pulse generators. Journal of Mining Science. 1998. 34(2). Pp 139–147. DOI:10.1007/BF02803446. URL: https://www.researchgate.net/publication/248775391_Wave_processes_when_driving_metal_pipes_into_the_ground_using_shock-pulse_generators.
Smirnov, A.L. Computation of the process of impact submersion of a pile in the ground - Part I. Mathematical modeling. Soviet Mining Science. 1989. 25. Pp. 359–365. DOI:10.1007/BF02528556. URL: https://link.springer.com/article/10.1007/BF02528556.
Aleksandrova, N.I. Numerical-analytical investigation into impact pipe driving in soil with dry friction. Part I: Nondeformable external medium. Journal of Mining Science. 2012. 48. Pp. 856–869. DOI:10.1134/s1062739148050103. URL: https://arxiv.org/ftp/arxiv/papers/1312/1312.1582.pdf.
Ambraseys, N.N., Smit, P., Douglas, J., Margaris, B., Sigbjörnsson, R., Ólafsson, S., Suhadolc, P., Costa, G. Internet site for European strong-motion data. Bollettino di Geofisica Teorica ed Applicata. 2004. 45(3). URL: http://www.isesd.hi.is/ESD_local/frameset.htm.

Еще

Статья научная