Vibration-protective properties of the suspension with smooth regulation of inelastic resistance in the vibration cycle

A number of works with the participation of the authors of this article [1–20] are devoted to the study of vibration-protective properties of single-mass and two-mass oscillatory systems with instantaneous regulation of damping in the oscillation cycle and the development of designs of adjustable shock absorbers.

These studies have shown that with optimal instantaneous control, damping is always turned off when the suspension passes its static position, and turned on when the moment of maximum compression or extension of the suspension is reached. Such an algorithm for damping control in the oscillation cycle provides a significant decrease in the amplitudes of vertical displacements of the sprung mass, and, consequently, heat generation in the shock absorbers. However, in this case, a decrease in the amplitudes of vertical accelerations occurs in a narrow range of resonant frequencies of vibrations of the sprung mass. In addition, the use of the optimal instantaneous regulation of damping in both dual-mass and single-mass oscillatory systems sets a complex (abrupt) nature of the change in the vertical accelerations of the sprung mass, which is associated with a sharp deactivation of damping in the middle (static) position, which does not contribute to an increase in the smoothness of the vehicle [14, 16].

In order to eliminate jumps in vertical accelerations and reduce their maximum values, the authors of the article proposed an instant (smooth) decrease in the shock absorber resistance in the zone of static position. Below is a theoretical analysis of the vibration-protective properties of a single-mass single-support suspension with two algorithms for smooth regulation of damping in the oscillation cycle considered below (Fig. 1). The mathematical model of this oscillatory system is written by the following differential equation:

mz + uk ( z - q ) + c ( z - q ) = 0 , (1) where m – sprung mass; k – damping factor; c – suspension stiffness; q – coordinate of the disturbing effect; z – movement of the sprung mass; u – parameter for controlling the shock absorber resistance.

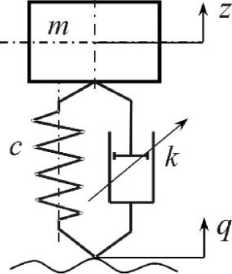
Fig. 1. Design diagram of a single-mass single-support oscillatory system with an adjustable damper

In both algorithms, damping is activated almost instantly when the direction of movement of the shock absorber piston is changed. However, the speed of compression or expansion of the shock absorber in this case increases smoothly from zero, which does not cause a sharp increase in the resistance force, and hence the acceleration of the sprung mass.

In the first algorithm, the inelastic resistance decreases linearly when approaching the neutral (stat- ic) position of the piston by an amount Δ1 and is reset to zero when a static position is reached, which can be described by the following expression for the shock absorber resistance control parameter u: 0     at (z - q) • (z - q) > 0,

u = <

k-ql At

at ( z - q ) • ( z - q ) <  0 и | z - q | <  A_t,

t        at ( z - q ) • ( z - q ) <  0 и | z - q | >  A₁.

In the second algorithm, the resistance decreases linearly with distance from the neutral (static) position of the piston and is reset to zero when the piston distance is reached Δ 2 , which can be described by the following expression for the shock absorber resistance control parameter u :

0 at ( z - q ) • ( z - q ) >  0 и | z - q | >  A₂,

u = <

t -

t- q A 2

at ( z - q ) • ( z - q ) >  0 и | z - q | <  A₂,

t          at ( z - q ) • ( z - q ) <  0.

• 1.    Analysis of the results of theoretical studies of vibration-protective properties of a singlemass single-support suspension with smooth regulation of damping in the vibration cycle

Fig. 2 shows oscillograms of a single-mass oscillatory system with damping control according to algorithm (2), and Fig. 3 shows the corresponding operating diagrams of the suspension with non-instantaneous switching off of damping at a resonance frequency i = 1 and v ⁼ 0,92 and at a resonant frequency i = 2 and v ⁼ 0,49. Here у - relative attenuation coefficient; i = ш/ш₀ — forced vibration relative frequency, ω 0 – natural frequency of sprung mass, ω – frequency of forced vibrations of the sprung mass.

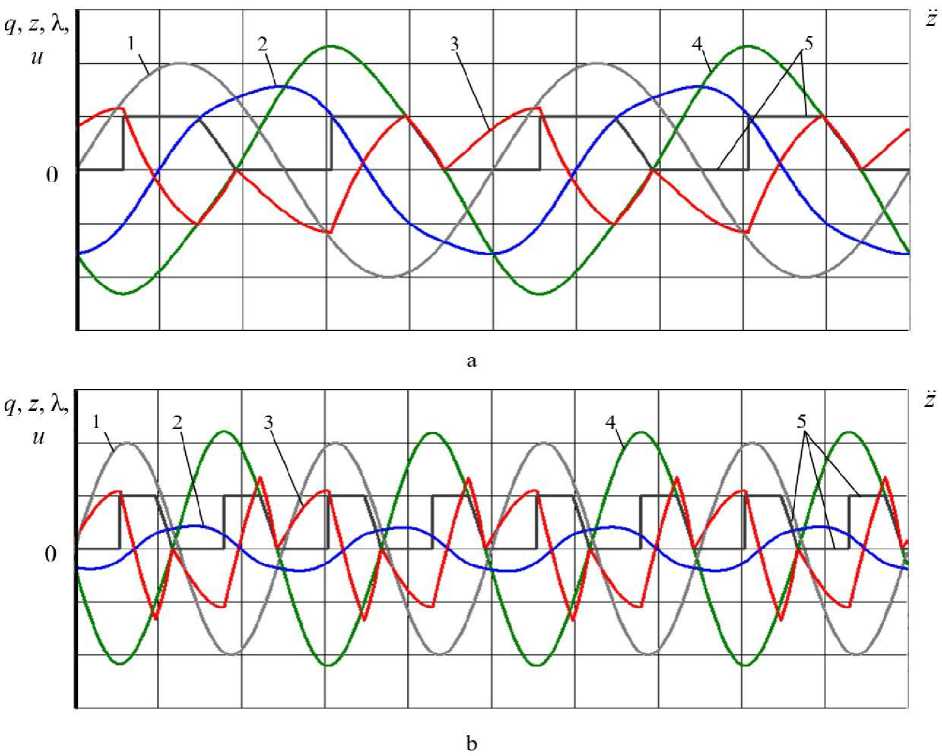
Fig. 2. Oscillograms of the suspension with damping control according to the algorithm (2): a – at ι = 1 and ψ = 0,92; b – at ι = 2 and ψ = 0,49; 1 – kinematic disturbance;

2 – absolute movement of the sprung mass; 3 – sprung acceleration;

4 - relative displacement of the sprung mass (suspension deformation X = z - q );

5 – control parameter u

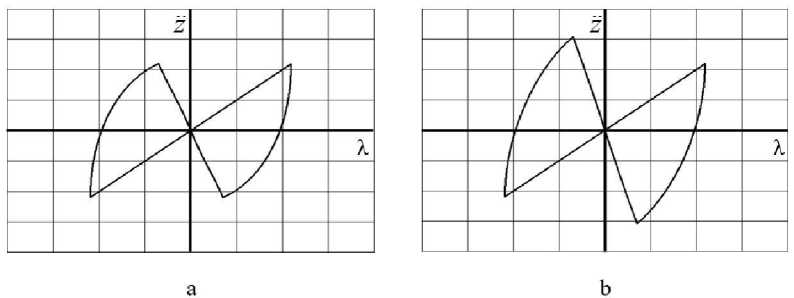
Fig. 3. Working diagrams of the suspension with damping regulation according to the algorithm (2): a – at ι = 1 and ψ = 0,92; b – at ι = 2 and ψ = 0,49 ; λ = z – q

From the analysis of the oscillograms of the vertical accelerations of the sprung mass with non-instantaneous switching off of damping (Fig. 2, curves 3), it can be seen that the accelerations have no discontinuities, and their ranges in comparison with the optimal instantaneous regulation [16] are reduced by about 25 %. From the analysis of the working diagrams in Fig. 3, it can be seen that the heat release in the shock absorber, determined by the area of the “butterfly” loop, increases insignificantly with an increase in frequency by 2 times.

Fig. 4 shows oscillograms of the suspension with damping control according to algorithm (3), and Fig. 5 shows the corresponding operating diagrams of the suspension with non-instantaneous damping control at the resonance frequency i = 1 and v = 0,92 and at a resonant frequency i = 2 and v = 0,49.

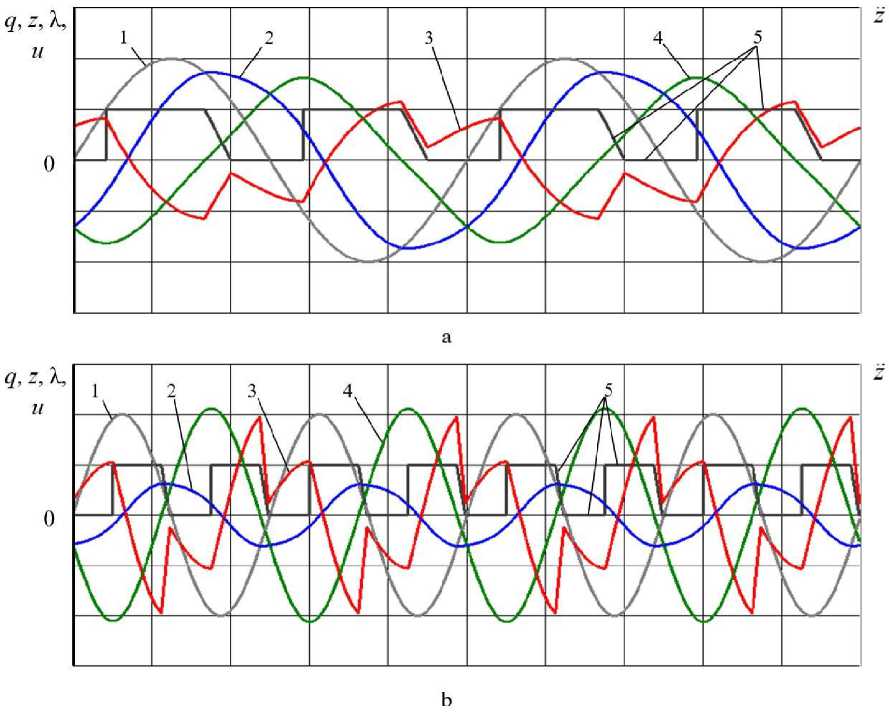
Fig. 4. Oscillograms of the suspension with damping control according to the algorithm (3): a – at ι = 1 and ψ = 0,92; b – at ι = 2 and ψ = 0,49; 1 – kinematic disturbance;

2 – absolute movement of the sprung mass; 3 – sprung acceleration;

4 - relative displacement of the sprung mass (suspension deformation X = z - q );

5 – control parameter u

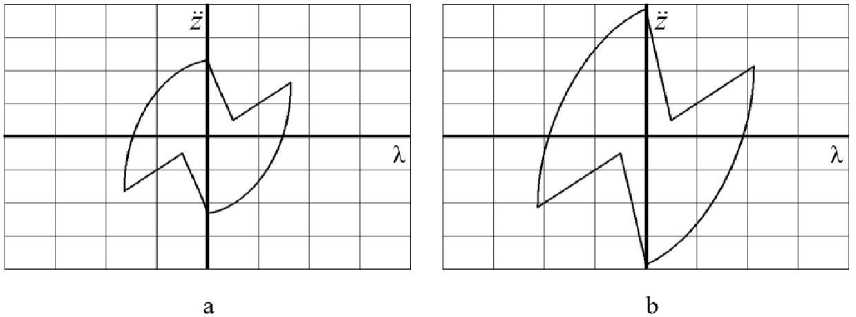
Fig. 5. Working diagrams of the suspension with damping regulation according to the algorithm (3): a - at i = 1 and ф = 0,92; b - at i = 2 and ф = 0,49; X = z - q

Fig. 6 shows the frequency response of displacements and accelerations of the sprung mass on the

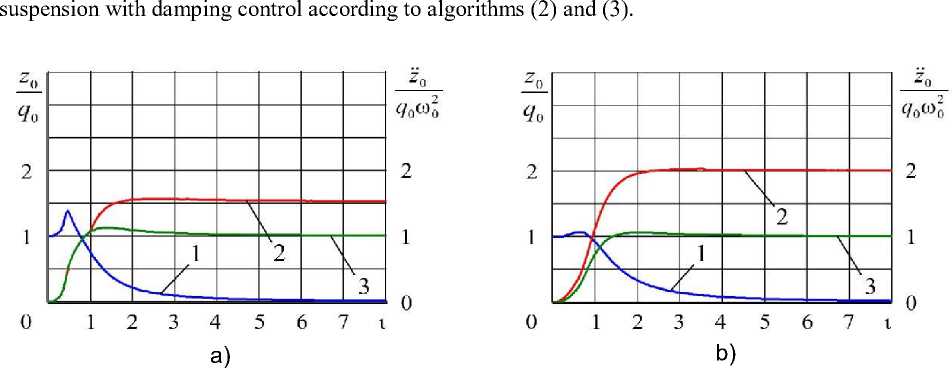
Fig. 6. Frequency response of displacements and accelerations of the sprung mass on the suspension: a) and b) – with damping regulation according to algorithms (2) and (3);

1 and 2 – absolute displacements and accelerations of the sprung mass;

• 3 – relative displacement of the sprung mass;

• 2.    Conclusions

z 0 – the amplitude of the absolute oscillations of the sprung mass, q 0 – kinematic disturbance amplitude

From the analysis of the graphs in Fig. 6 it can be seen that both algorithms for regulating the resistance in the oscillation cycle provide a 2-fold reduction in the natural frequency of the suspension and obtain practically non-resonant frequency response of the absolute and relative displacements of the sprung mass with a dynamic coefficient close to or even less than 1, as well as stabilization of the acceleration of the sprung masses in the zone outside the zone. At the same time, the minimum values of accelerations and absolute displacements of the sprung mass in almost the entire frequency range provide non-instantaneous resistance control according to algorithm (2) (curves 2 and 3 in Fig. 6a), and the minimum relative displacements in the low-frequency oscillation zone (before ι = 3) – algorithm (3) (curve 3 in Fig. 6b).

In conclusion, it should be noted that the optimal characteristics of suspension systems with smooth regulation of damping in the oscillation cycle in the entire frequency range are achieved when the maximum inelastic resistance changes according to the same law for all both cases ^(i), close to hyperbole [6]. In comparison with an unregulated shock absorber, the proposed algorithms for smooth cyclic damping control provide a significant reduction in the vibrations of the sprung mass in the entire frequency range. Therefore, it is necessary to search for simple structures that implement non-instantaneous regulation of the inelastic resistance of the suspension in the vibration cycle.

• 1.    A smooth decrease in damping in the area of the middle position of the suspension when adjusting the damping according to algorithms (2) and (3) allows to reduce the resonance frequency by 2 times in comparison with an unregulated suspension and to reduce the vertical acceleration of the sprung mass by 25 % in comparison with the suspension with optimal instantaneous damping regulation.

• 2.    The minimum values of accelerations and absolute displacements of the sprung mass practically in the entire frequency range provides smooth control of the resistance according to the algorithm (2).

• 3.    Minimum relative displacements in the low-frequency vibration zone (up to ι = 3) provides smooth regulation of resistance according to the algorithm (3).

• 3.    Acknowledgements

The work is financially supported by the Ministry of Science and Higher Education of the Russian Federation as part of a comprehensive project to create high-tech production “Creation of high-tech production of an unified family of vehicles “Arctic Bus” to organize the safe transportation of passengers and mobile points of the social sphere in the regions of the Far North in conditions of low temperatures

(up to minus 50 °C) to ensure the connectivity of the territories of the Arctic zone of the Russian Federation” under the agreement no. 075-11-2021-058 dated 06/25/2021 (Government Contract ID 000000S407521QLY0002).