Виброробот для вертикального движения по металлической шероховатой поверхности

• 1.    Описание вибрационной мобильной системы. Робот двигается под действием силы трения, возникающей на контакте корпуса и металлической шероховатой поверхности. Управление величиной и направлением силы трения осуществляется за счет вращения деба-лансных внутренних масс и переменного усилия прижатия корпуса к шероховатой металлической поверхности.

• 2.    Математическая модель движения робота. Дебалансы будем считать материальными точками, расположенными в центре масс дебалансов, а корпус робота рассматриваем как материальную точку. Массы дебалансов равны. Робот движется в системе координат XOY. На механическую систему наложены связи:

  Ф 1 = ^П - Ф 2

  x = 0

  
  
  
  

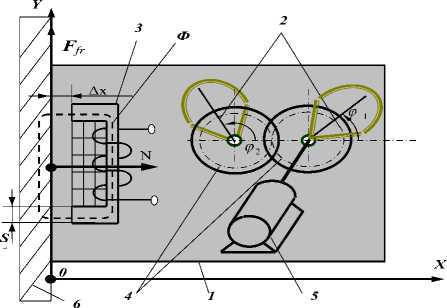
Рис. 1. Схема робота: корпус 1, дебалансы 2, электромагнит 3, зубчатые колеса с передаточным отношением 1 (синхронизатора) 4, электродвигатель постоянного тока 5

Для составления математической модели применим уравнения Лагранжа-Максвелла, система уравнений будет состоять их 2 уравнений электрических цепей (m=2) и 2 уравнений, описывающих механическую часть системы (n=2) [5]:

d dL dL --+ дФ1 дТ д<р 1 = E1 dt а (р 1 d dL dL дТ ---+ — = E 2 dt а у 3 d y 3 д y 3 d dL dL дТ — --+ — = Q1 dt • a q Я dq я дЧ Я d дL   дL   дТ

--•----1--•—

. dt a q* M   ^d q^M   д ^ м

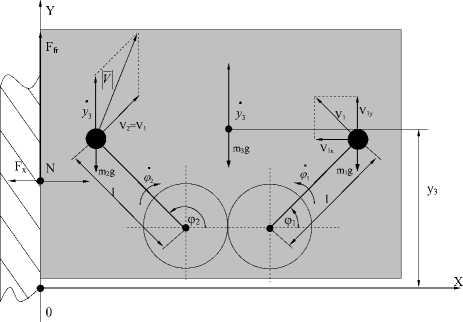
Рис. 2. Расчетная схема робота

Для определения диссипативной функции, кинетической и потенциальной энергии рассмотрим расчетную схему механической части робота, приведенную на рис.2. Выражение для кинетической энергии будет иметь вид:

Определим функции входящие в систему уравнений (2). Функцию Лагранжа (L) будем искать как сумму кинетической, потенциальной и магнитной энергии

• ²

•         •        • m • y

T I У з J + Т я I Ф 1 J + Т д Ы =   2 +

. (5)

I L ^JЯ '^Ф1

J 2

⁺ т ^Г y 3 J

••

•

L = ^TK I y 3 I ^{+ Т}д I ^ф 1 I ^{+ Т}я I ^ф 1 I П К ⁽ y 3 ) ^ПД ^{( ф} 1 ^{) + W}МД ⁽ I Я ^{) + W}MM I M )

•

•

•

+ 2 • y 3 -| р ₁1 1 cos ( p ) + | р 1

(3)   Диссипативная функция механической системы:

где Тк I yз I; Тд I ф1 I; Тя I ф1 I -кинетическая энергия корпуса, дебалансов и вала двигателя; пк (yз); Пд (р) - потенциальная энергия корпуса и дебалансов; WM^(Iя) - магнитная энергия двигателя; WMM (Iм) - магнитная энергия в воз- душном зазоре электромагнита.

Диссипативная функция ( Т ) будет иметь вид:

••

Т = Т м | у 3 | + Т м Ф 1 + Т e ( I Я ) + Т e ( I m )

V ) V )                     .       (4)

• • где Тм I y 3 I; Тм I ф1 J - диссипативные функции корпуса и дебалансов; Тe(1 я )5 Тe(IM ) - диссипативные функции двигателя и электромаг- нита.

•

У м I y 3

м

Ф 1

A y 3 у 3 + А ф 1 Ф 1

где A y ₃, А_{ф 1} - значение вязкости.

Потенциальная энергия механической системы:

П(У 3)+ П(Ф1) = m 3 g- У 3 + 2 m1 g(У 3 +1 - §ь(Ф1))

.                                                              (7)

Для вращения дебалансов используется двигатель постоянного тока, тогда

L I ²              • L q*²

W МД ⁽ I Я ) = ¹¹2 ^{Я +} L 12 I Я Ч с ⁺ 22 2 с - магнитная энергия двигателя, L 11 и L 22 – коэффициенты самоиндукции соответственно подвижного и неподвижного контуров; L 12 – коэффициент взаимной индукции контуров, J я – момент

• инерции вала двигателя, qс - ток в цепи статора. L12 зависит от ориентации ротора и статора, т.е. от обобщенной координаты φ1, следовательно L12= L12(φ1).

Диссипативная функция для двигателя:

W e ( I я ) =

.

В качестве магнитного привода предлагается использовать П-образный электромагнит. Энергию магнитного поля в воздушном зазоре электромагнита определим по формуле:

Для дифференциального уравнения описывающего движение по обобщенной координате y 3 непотенциальной силой является сила трения, которая представлена кусочнонепрерывной моделью:

- к- N - sign ( у 3 ),

w

ММ

Ф² - A x

2 - д 0 - 5 - z²

Q y 3 = F TP = ‘   ^FPД ,

^- К ^- N ^- sign ^{( F}PД ),

• ^у 3 ^ ⁰;

• У 3 = ^0,| F pg ^ к >^- N ;

• У 3 = 0,|F pд | > К о - N .

где Ф – магнитный поток, возникающий в магнитном контуре сердечника, ^д ₀ - магнитная проницаемость, S – площадь воздушного зазора , z - число витков проводника с током, A x - зазор между металлической поверхностью и электромагнитом.

Диссипативная функция электромагнита:

^Т М ⁽ I М ) = ~ ^R M ' I М

2            .(9)

Функции L и Т будут иметь вид:

• ²

L = m 3 ^- у 3

+ m₁

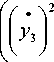
+ 2 у 3 -| ф 1 l 1 cos ^ ) +[ ф_хl

• • ²

. Jя ■ ф               .    ( . , • ( w   Ф2-Ax,

+     — mз g- Уз - 2mi g(Уз + l- <ф))+ т

• 2                                          2 - д - 5 - z

•

+ L ^ + L 12 1 Я q c + L 2 q

•                 •

= Д у 3 У 3² + _{Цф Х} ф ² + R _M -1М ² + К _я I _я ²

'      2        2         2         2 . (11)

где F РД – проекция на ось Y равнодействующей всех сил, приложенных к конструкции робота, кроме силы сухого трения, κ – коэффициент трения скольжения, κ 0 – коэффициент трения покоя, N – реакция опоры, равная тяговому усилию развиваемому электромагнитом.

Для П-образного электромагнита непотенциальную силу, действующую на корпус со стороны электромагнита, будем рассчитывать по формуле [6]:

Ф ²

2 - д ₀ - 5 - z²

Тогда нормальная реакция опоры представлена в следующем виде:

N = F x

Ф ²

2 д ₀ - 5 - z²

Продифференцируем полученные функции L (9), ψ (10) по соответствующим координатам получим систему дифференциальных уравнений, описывающих поведение электромеханической системы:

••

Ф 1 =

• ••                                    •

  
  

2 - у 3 - m i - 1 - cos ( ф 1 ) - д i - ф 1 - 2 m i - g - 1 - cos ( ф 1 ) + k _m I я

< • ^ ²                         •

• ••      ^{2 - m} 1 ^- ф 1 I ^{- 1 - sin (} ф 1 ^)- Д _{у 3} ^- у 3

у 3 =--------------------------------------,

••

2 - m ₁ -1 ф ' ₁ I - 1 - cos ( ф ' ₁ ) - m ₃ g - 2 m ₁ g + F_TP

( m ₃ + 2 - m 1 )

•              Ф-Nx

Ф = U_м ( t ) - R_M--- Д 0 - 5 - z

I Я

U я ⁽ t ) ^{- R}я¹ я ^- k_E ф 1 L_Я

Для решения системы (15) применялся метод численного интегрирования Верле [7]. Напряжение U М ( t ) будем моделировать следующим образом:

U м ( t ) = U 1 +

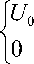
если sin( ® - t + a ) >  0 если sin( ^ t + a ) <  0

графика ускорения на рис. 4 видно, что в начальный момент времени на систему воздействуют большие значения ускорений. Увеличим и совместим графики ускорения корпуса и угловое ускорение вала двигателя. Полученные зависимости приведены на рис. 5.

где U 1 – постоянная составляющая напряже-

ния, подаваемого на электромагнит.

Напряжение в цепи статора двигателя имеет постоянную фиксированную величину U Я ( t ) = const и соответствует величине, при

которой частота вращения вала равна частоте периодической составляющей напряжения пи-• \ тания электромагнита ® = I Ф1 I ,

V 7 ср

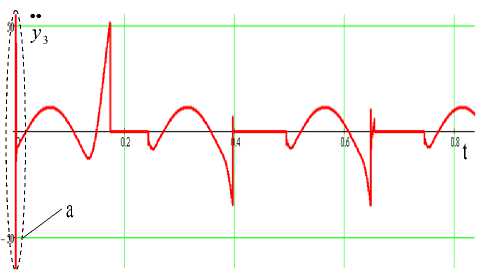
Рис. 4. График ускорения корпуса робота

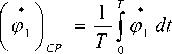
Для моделирования выбраны следующие значения параметров электромеханической системы: k =0,7, ω=25 1/c, m 1 =0,1 кг , m 3 =0,1 кг,

| н I l=0,05 м, цф=1 нм/с, цу=1 V м^с J, z=1000, Δx=0,001 м, S=0,0001 м2, ψ=π, RМ = 30 Ом, RЯ=0,8 Ом, Kω=1,3 нм/А, Kε=0,68 В/с, UЯ (t) = 32,5 В, U1=0 В. Начальные условия

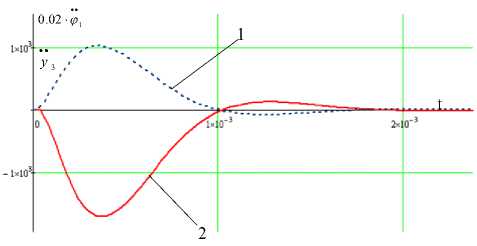
Рис. 5. Увеличенные, в области переходного процесса, участки графиков углового ускорения дебалансов и ускорения корпуса (1 – угло-

для моделирования поведения электромеханической системы:

у з = 0; у з = 0; у з = 0; ф i = 0;

^9 1 = 0; ф 1 = 0; Ф = 0; Ф = 0

Рис. 3. График перемещения корпуса робота по вертикальной поверхности

вое ускорение дебалансов 0,02 • ф 1 ,2 - уско-

• • рение корпуса робота y 3 )

Как показывают графики, соскальзывание корпуса с вертикальной поверхности вызвано разгоном двигателя до требуемого частоты вращения и вследствие этого большими

значениями

касательно

силы

инерции

, входящей в систему урав-

Начальное движение системы начинается с соскальзывания, данный участок графика расположен в области ( I ) и характеризует переходный процесс, происходящий в системе. Дальнейшее движение корпуса робота происходит в области ( II ) и носит характер установившего движения вертикально вверх. На участке (а)

нений (15).

Установившийся режим движения робота (рис. 6) состоит из 3 фаз. Во время фазы движения T 1 корпус робота покоиться на одном месте, происходит остановка. Далее при T 2 мобильный объект соскальзывает вниз, силы трения недостаточно, для того, чтобы скомпенсировать равнодействующую силу, приложенную к корпусу. При T 3 мобильный робот поднимается вверх под действием усилия, развиваемого дебалансами.

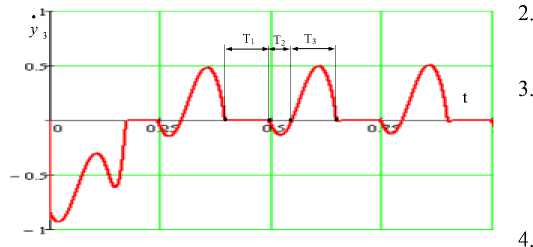
Рис. 6. График скорости корпуса робота

Работа выполнена в рамках ФЦП «Научные и научно- 5. педагогические кадры инновационной России на 20092013 г.» Госконтракт №П621 от 18.05.2010г и при поддержке РФФИ проект №10-08-00769.             6.