Video shots’ matching via various length of multidimensional time sequences

Clustering data arrays takes up an important place in a general problem of Data Mining [1-12]. There are lots of different methods nowadays for solving the task. A special attention in clustering data arrays is given to issues related to time series processing, which usually imply (except for actual clustering) segmentation, detection of property changes (fault detection) and abnormal outliers [13]. Thereby, clustering should be performed not only in space, but also in time.

When it comes to clustering time series, it should be kept in mind that conventional popular methods come out to be effectless (as a matter of thumb). It happens due to the fact that all observations are strictly ordered (one by one), and no data mixing is absolutely impermissible. Time series properties to be clustered in a feature space may be varying with time in such a way that the same implementation at different time intervals can have various characteristics. After all, the most complicated thing is that sequences to be processed may have a different length. This fact technically does not allow using traditional metrics which are typical for the cluster analysis.

In addition to that, the clustering task for time series appears quite often while processing medical observations, financial indexes, audio and video signals [14, 15]. For this purpose, as a general rule, it is assumed that initial data can be converted into a form of onedimensional sequences. In this respect, it seems advisable to produce effective methods for clustering / segmentation / detection of property changes in multidimensional (both vector and matrix) time series of various lengths, which are numerically simple and provide reduced processing time, which means that they ensure prerequisites for online video processing.

Video processing explores visual information particularly to classify videos into meaningful categories according to semantics such as presence of objects or any other event. Thereby, a very challenging problem arises when it comes to simulation of visual attention mechanisms for content-based structuring of video streams represented by time varying images with a spatial intensity distribution changing through time. A visual attention model should be focused on decision making. Its details within a field of view are important and should be focused upon as well as filtered into a background [16]. The bottom-up visual attention is understood as a strong ‘general contrast’ of a region to its surround and uniqueness of this region. Prioritizing attention in video analysis is linked with intensity, color, orientation, motion, flicker, rarity etc. and is associated with a point, a blob or the sliding window (a subframe) processing paradigm since saliency maps are the foci of attention (saliency maps’ formation within an image consists in emphasizing all inputs that differ from their surrounding inputs) [17, 18]. The simplest approach to producing time series is to determine fixed-sized regular regions around the most salient points. Some more sophisticated and valid approaches integrate temporal and spatial segmentations to determine irregularly shaped attention regions. Anyway, obtained video shots that reflect high stable salience are key units of temporal video segmentation which may be explained locally in time as a sequential 2-class clustering problem (“a scene change” and “no scene change”). Hierarchical shots’ processing is intended to bridge the gap between low level retrievable features and high level perception that may provide visual content identification and search technologies.

The issues mentioned above put the problem of comparing image sequences into a category of toppriority problems, since a valid comparison of video sequences predetermines the clustering efficiency and interpretation on the whole. Some privilege during comparison should be given to metrics [4, 19], but weakening some of the metric axioms may create preconditions for obtaining effective computational models of indexing and searching in Content Based Video Information Retrieval systems.

The remainder of this paper is organized as follows. Section 2 describes evaluation of time series similarity on the basis of Dynamic Time Warping (DTW). Section 3 is devoted to time series clustering with the usage of the iterative Dynamic Time Warping (IDTW). Section 4 presents an adaptive technique for time series reduction. Section 5 presents experimental results and discussions on applications’ peculiarity. Conclusions and future work are given in the final section.

• II.    Evaluation of Time Series Similarity based on Dynamic Time Warping (DTW)

Regarding clustering problems for time series, those methods have got widespread which are premised not on the use of a certain metric, but on a similarity measure describing a shape of these series [7]. Within that narrative, the most widespread measure is a Dynamic Time Warping (DTW) measure [20, 21] that enables to compare sequences of different lengths.

A backbone of the DTW approach can be described as follows: let us assume there are two one-dimensional sequences of various lengths X = { x (1), x (2),..., x(t ),..., x ( N ) } and Y = { y (1), y (2),..., y (l ),..., y (M ) } , N * M .A distance between these sequences should be defined in order to solve the clustering problem from this point on. A [ N x M ] - matrix is taken into consideration. Its elements are distances d ( x ( k ) , y ( l )) (usually the Euclidean ones) between all timings in the time series X and Y . Then a so-termed warping path W = { w_x , w ₂,..., w_L } is introduced next (here max ( N , M ) <  L <  M + N + 1, w q = ( d ( x ( k ) , y ( l )) ) , q = 1,..., L ). One can identify similarity between X and Y with their help.

Several conditions are imposed on the warping path:

–

boundary conditions w = ( d ( x ( 1 ) , y ( 1 )) )    and

Wl = ( d ( x ( N ) , y ( M )) ) imply that the warping path starts and ends in diagonally opposed corners of the distance matrix;

–

w q — 1

continuity conditions denote that

= (d (x(k'),y (l'))) ।, k -k' < 1, l -1' < 1

for some w_q = ( d ( x ( k ) , y ( l )) ) ;

– monotonicity conditions indicate that w_q_ ₍ = ( d ( x ( k ' ) , y ( l '))) ^ k - k '> 0, l - 1 '> 0 for some w_q = ( d ( x ( k ) , y ( l )) ) .

relations are held

relations are held

A path is chosen as a similarity measure to minimize an objective function

Il L^x\

DTW(x,y) = min ^ yL ydd (x(к),y(l)B

W I      l=1

i.е. connecting all points of the analyzed time series.

A search for the optimal path is particularly based on the ideas of dynamic programming using a recurrent relation

D ( k, l) = d (x (k ), y (l)) +

+ min { D ( k , l - 1 ) , D ( k - 1, l ) , D ( k - 1, l - 1 )}   (2)

where D ( k , l ) is a cumulative distance between observations x ( k ) and y ( l ) . The cumulative distance D ( N , M ) is actually a dynamic temporal distance, i.e.

DTW ( x , y ) = D ( N , M ) . (3)

This approach was covered in [14] for a case of multidimensional time series where a component x ( k ) , y ( l ) is a ( n x 1 ) -vector of observations. In this instance, the Euclidean norm is utilized as a distance between x ( k ) , y ( l )

d 2 ( x ( k ), y (l)) = | x ( k )-y (l )||2

given that the expressions (1)-(3) also remain unchanged.

Applying the quadratic norms in problems of time series processing is limited to the fact that results obtained are highly sensitive to outliers and abrupt changes. Due to this, the Dynamic Time Warping based on derivatives (Derivative Dynamic Time Warping – DDTW) was introduced in [22] where estimates based on differences d (x (k), y (l)) are used instead of the distance d ( x ( k ), y (l)) where x (k) =

(x ( k )- x ( k -1) + ( x ( k +1)- x (k -1)) /2) 2

(y (k)-y (k - 1)+(y (k +1)-y (k-1))/2)  (5)

It will be understood that all the conversions described above are valid for scalar, vector and matrix signals (4), (5).

Although DTW is not generally a metric, but only a similarity measure, it is emphasized in [23] that this measure is the best choice precisely in the context of clustering in the matter of an obtained accuracy. The main DTW shortcoming is high complexity of computing feasibility, especially when it comes to handing long enough time series. On such occasions, using DTW does not look effective enough.

• III.    Clustering Time Series in Terms of the Iterative Dynamic Time Warping (IDTW)

Unwieldiness of the conventional DTW forced to look for alternative approaches to assessing the proximity of time series, where one of the most efficient gimmicks is the iterative Dynamic Time Warping [15]. This method is founded on the reduction idea for initial sequences, when segments of these sequences are replaced by corresponding mean values. With that, initial sequences are divided into approximately equal intervals, and an amount of these intervals for series of different lengths is equal.

Thus, let us consider two sequences X and Y of lengths N and M observations accordingly. In a general case, X and Y may be scalar, vector and matrix series.

Let us distinguish observations x (1), x ([ N4 J), x (L N2 J), x ([3 N4 J), x ( N),

y(1), y (L M4 J), y (L M2 J), y (L3 M4 J), y(M)

(here L⁰J stands for a floor function) in each series and calculate mean values at the segments

x(1) x(LN4J),x(LN4J+1) x(LN2J), x (LN2J+1)-x 3 N4 J), x (L3 NA J+1)-x (N);

y (1)-y (LM4 J), y (LM4 J+1) - y (LM4 J)•

-y (LM-2J+1)- y (L3 M4 J), y (L3 M-4 J+1)- y (M).

In this way, reduced sequences x (1), x (2), x (3), x (4); y (1), y (2), y (3), y (4) are regarded. It seems rather easy to estimate similarity between components of these reduced sequences with reference to the traditional DTW with a (4 x 4)- distance matrix. Obviously, these reduced series may be clustered by means of any well-known algorithm.

Needless to say that this sort of approximation is too rough, and a clustering quality proves definitely to be low. As a consequence, each of the four formed segments is divided in half at the next stage, for example, two intervals

x(1)-x(LN8J),x(LN8J+1)-x(LN4J)are formed instead of x

( 1 ) - x ( L N 4 J )

and so on. New mean

values x ( 1 ) , x ( 2 ) ,..., x ( 8 ) ; y ( 1 ) , y ( 2 ) ,..., y ( 8 ) are introduced at these newly formed segments, and similarity between them is estimated based on a ( 8 x 8 ) - distance matrix.

It is clear that distance matrices acquire dimensionality of ( 16 x 16 ) , ( 32 x 32 ) and so on. Thus, the task becomes substantially more complicated. For that reason, from the standpoint of computation costs, it’s much easier to organize fragmentation of the original series not into 4, 8, 16, … blocks, but, for instance, into 4,5,6, … intervals, which drastically simplifies the task.

Having formed an array of the reduced series, where every series contains an equal number of timings, that’s really trivial to solve the task of clustering them on the ground of a proposed modification of the k - means method. Its algorithm may be presented in the following manner.

Suppose that there is an array of time sequences x , x ,..., x ,..., x , where each one consists of

N , N ,..., N ,..., N observations.

Step 1. After the first stage of reduction, we acquire the same x , x ,..., x , but each of them contains only 4 timings in this case.

Step 2. Then m centroids C , C ,..., C are arbitrarily built up in the form of sequences, which contain the same amount of timings as the reduced series x do.

Step 3. At the next stage, every x is assigned to one of the centroids according to the rule x e Clj   if   IDTW (x, Cj ) < IDTW (xq, cz)   for q = 1,2,...,Q; j, l = 1,2,...,m .

Step 4. After this, the initial centroids are recalculated according to the expression C = —— ^ x , i.e.

j  Njx^q averaging is performed for all the reduced series for each cluster. In this case, a situation may happen, when the newly formed centroids have a bigger number of timings compared to the processed series. When this occurs, the centroids are reduced according to the same rules as for the original series.

Step 5. A process of centroids’ refinement is carried out until a deviation norm (either the Euclidean one or the spherical one) of refined centroids Cnew exceeds some predetermined threshold 8 from those centroids Cold to have been obtained at the last iteration of the algorithm for all j .

In this instance, the algorithm either stops its work or performs a deeper reduction procedure of the time series with a larger number of timings.

As one can see, the proposed approach is easy to get implemented as opposed to the well-recognized methods of clustering time series of different lengths.

^T + ⁽ 0 ) =0,

Ш к ) = E ( x ( к ) - x - 0.5 ^ ) ,      (8)

T = 1

T * ( к ) = max T ( к ) . '   0< t <  к

The decision on an increase of the mean value is taken at the moment к = r , when the inequality

T *+ ( r ) - T + ( r ) > x               (9)

The discussed above procedure of time series reduction contains a reasonably large level of subjectivity and is by no means related to properties of analyzed sequences. From this perspective, it is more efficient to replace the time series with their mean values only at stationary areas, while their statistical properties remain virtually unchanged. For this purpose, it is expediential to use methods of detecting changes in mean values. The most effective method is the one driven by the Page-Hinkley criterion [24].

In      summary,      given      a      sequence

X = { x (1), x (2), ...,x ( к ),..., x ( N ) } and it is supposed that its mean has a value of x where 1 <  к <  r and r <  к . To take advantage of the Page-Hinkley criterion, it is obligatory to set a minimum value of a shift 5 , which accounts for disruption of stationarity in the process under control. But given that a sign of this shift initially unidentified, the procedure of property detection should contain two parts. The first part of the procedure is meant for detection of the mean value’s decrease and may be presented in the form of

is met.

To implement the process control in a sequential mode, the adaptive modification (6)-(9) may be applied as follows

T - ( 0 ) =0,

T_ ( к ) = T_ ( к - 1 ) + x ( к ) - x + 0.5 5 ,

T *_ ( к ) = T ( к ) +

Г

T (к ) - T (k -1) +0.5 1 —

,    V( ^T - ( ^к ) - ^T - ( ^к - 1 ) ) ²

T •_( к)- T-( к )> x and

)

( ^T - ( ^к - 1 ) - ^T - ( ^к ) )

T + ( 0 ) =0,

T ( к ) = T ( к - 1 ) + x ( к ) - x - 0.5 5 ,

^T -⁽⁰⁾ =0.

' T - ( к ) - j ( x ( к ) - x , + 0.5 5 ) ,          (6)

T = 1

T * ( к ) = max T ( к ) .

0 <  к

<

T "Дк) = T (к) +

+0.5 1+

T ( к ) - T ( к - 1 )

J( ^T + ( ^к ) - ^T + ( ^к - I ) ) ²

)

( ^T + ( ^к - 1 ) - ^T + ( ^к ) )

The decision that a controlled mean value has significantly decreased should be made right at the moment к = r , when the inequality

^T + ( ^к ) - ^T *+ ( ^к ) > x .

T *— ( r ) - T — ( r ) > x

takes place. In this inequality, x is some threshold value to be chosen empirically.

A procedure for detecting an increase in the mean value has the form

Accordingly, the used procedures of the adaptive reduction (6)-(11) for time series improve efficiency of the iterative Dynamic Time Warping (IDTW) processes and therefore enhance the quality of clustering time series with different lengths.

• V.    Experiments

  While making our experimental research, we used time series generated by 40 sec video streams (i.е. each one contains 1000 frames) from “Destroyed in Seconds” by Discovery Chanel. This choice can be easily explained by a high dynamic of events’ semantics and various conditions of video registration that give us hope to wait for reliability and validity of results.

As a prototype for comparison of the proposed methods for detecting property changes in multidimensional sequences of various lengths, we used temporal analysis of segmentation sequences for each shot.

In other words, if x (t) is some video shot then its carrier D is presented as a set P of regions s , в =1, P . Since we consider only partitions, then Dx(t) = UpSp and

• V P ', P "e{ 1,2,..„ P } : p*p ^ s _p n s _p = 0 .

.

Let x ( t ' ) and x ( t ”) be two images from a video stream. The   segmentation/   clustering 5 ' = { s ‘ } ^     and

S " = { s i}Q-\ correspond to them. A comparison of two video shots in the space of segmentation is faster than in the space of images and more reliable than in the space of features of the low level. A metric for a comparison of two partitions / segmentations may be presented [25] in the form of

PQ

p(S', S ) = ^^card (s,As‘)card (s‘ n s )

i = 1 j = 1

where card ( • ) denotes cardinality of a set, and A marks an operation of symmetric difference of sets.

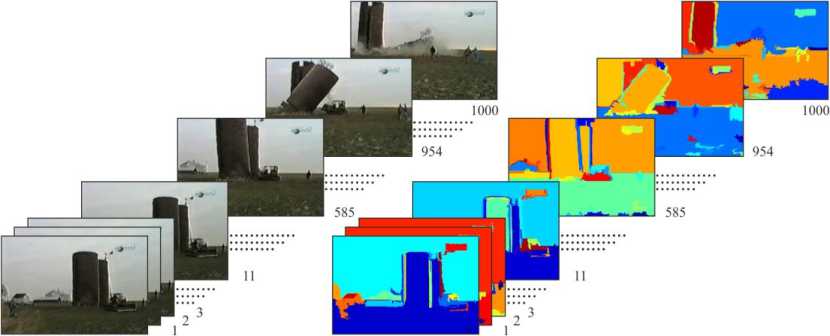
Fig.1. Examples of a video sequence and spatial segmentation of video frames

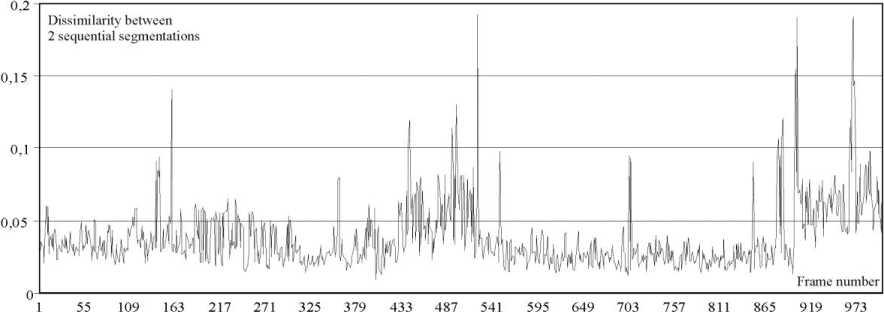
Fig.2. Differences between frames of a video sequence in the space of image segmentations

In Fig.1, there’s an example of video series and results of the spatial segmentation for each shot.

Fig.2 illustrates a difference between two sequential in time segmentations. One can see that peaks make it possible to determine borders of homogeneous in content sequences. However, it should be noted that when we have blurred boundaries of subjects (for example, as a result of a lap dissolve, fade, a side curtain wipe etc. as well as slow panning) a difference 11’ -1” | should grow in order to reliably detect changes of the video content.

Using local features of video frames for production of time sequences to be parsed along with privileges (like allocation of points or areas of interest; time savings) has also a number of shortcomings which are primarily associated with random fluctuations in a position of analyzed objects that is usually caused by “instability” of a shooting process. While forming time series, all these hardships can be avoided due to the usage of some integral characteristics of the regions which cover areas of interest and particularly textural features. One can see in Figs.3 and 4 examples for 16 and 8 adjacent rectangular windows that cover an area of interest.

There are results of temporal segmentation of a video sequence in Fig.5 (introduced in Fig.1). Clusters in time are marked with one color. Analyzing results for different video streams, we can claim that usage of the iterative dynamic time warping procedure (IDTW) gives the possibility for increasing a clustering quality of time series of different length.

Fig.3. A fragment for clustering in time (an example #1)

Fig.4. A fragment for clustering in time (an example #2)

Fig.5. Clustering a video sequence in time

• VI.    Conclusion

The method for detecting property changes in multidimensional sequences of various lengths within the scope of the iterative Dynamic Time Warping is presented in this article. The introduced method is premised on the adaptive reduction for time series. A modification of the k-means clustering method for reduced time series is also proposed here. The established procedure provides appreciably an opportunity to handle multidimensional sequences of both vector and matrix forms.

This scientific work was supported by RAMECS and CCNU16A02015.

• [1]    A.K. Jain and R.C. Dubes, Algorithms for Clustering Data . Englewood Cliffs, N.J.: Prentice Hall, 1988.

• [2]    L. Kaufman and P.J. Rousseeuw, Finding Groups in Data : An Introduction to Cluster Analysis. N.Y.: John Wiley & Sons, Inc., 1990.

• [3]  J. Han and M. Kamber, Data Mining : Concepts and

  Techniques . San Francisco: Morgan Kaufmann, 2006.

• [4]  G. Gan, C. Ma, and J. Wu, Data Clustering : Theory,

  Algorithms, and Applications . Philadelphia: SIAM, 2007.

• [5]    J. Abonyi and B. Feil, Cluster Analysis for Data Mining and System Identification . Basel: Birkhäuser, 2007.

• [6]  D.L. Olson and D. Dursun, Advanced Data Mining

  Techniques . Berlin: Springer, 2008.

• [7]  C.C. Aggarwal and C.K. Reddy, Data Clustering :

Algorithms and Applications . Boca Raton: CRC Press, 2014.

• [8]    C.C. Aggarwal, Data Mining . Cham: Springer, Int. Publ. Switzerland, 2015.

• [9]    Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and V.O. Samitova,"Fuzzy Clustering Data Given in the Ordinal Scale", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.1, pp.67-74, 2017.

• [10]    Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, and V.O. Samitova,"Fuzzy Clustering Data Given on the Ordinal Scale Based on Membership and Likelihood Functions Sharing", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.2, pp.1-9, 2017.

• [11]    Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, V.O. Samitova,"Possibilistic Fuzzy Clustering for Categorical Data Arrays Based on Frequency Prototypes and Dissimilarity Measures", International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.5, pp.55-61, 2017.

• [12]    Zh. Hu, Ye.V. Bodyanskiy, O.K. Tyshchenko, V.M. Tkachov, “Fuzzy Clustering Data Arrays with Omitted Observations”, International Journal of Intelligent Systems and Applications (IJISA), Vol.9, No.6, pp.24-32, 2017.

• [13]    N. Begum, L. Ulanova, J. Wang, and E. Keogh,

  “Accelerating dynamic time Warping Clustering with a Novel Admissible Pruning Strategy”, Proc. of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp. 49-58, 2015.

Sergii Mashtalir graduated (M.Sc.) from Kharkiv National University of Radio Electronics ( KhNURE ) in 2001. He got his PhD in 2005 and Dr. Habil. Sci. Eng. in 2016.

He is currently working as Professor of Informatics Department at KhNURE. He has about 100 scientific publications including 2

monographs. His research interests are image processing and recognition, video parsing, content based image and video retrieval.

Oleksii  Tyshchenko graduated from

Kharkiv  National University of  Radio

Electronics in 2008. He got his PhD in Computer Science in 2013. He is currently working as a Senior Researcher at Control Systems Research Laboratory, Kharkiv National University of Radio Electronics. He has currently published more than 50 publications. He is a reviewer of such journals as Neural Computing and Applications (NCAA); Soft Computing (SoCo); Evolving Systems (EvoS); Neurocomputing (NeuroComp); IEEE Transactions on Cybernetics;  IEEE

Transactions on Fuzzy Sets and Systems; Fuzzy Sets and Systems; Pattern Recognition Letters.

His current research interests are Evolving, Reservoir and Cascade Neuro-Fuzzy Systems; Computational Intelligence; Machine Learning; Deep Learning; High-Dimensional Fuzzy Clustering.

Mykhailo Stolbovyi graduated from Kharkiv National University of Radio Electronics in 2007. He is a PhD student in Computer Science at Kharkiv National University of Radio Electronics. His current interests are image and video processing, video clustering, and computational intelligence.