Виртуальное моделирование робота SCARA в Unity3D

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №7 2025

УДК 004.942:004.896                               

В последние десятилетия робототехника стремительно развивается, охватывая всё больше областей, от промышленной сборки до медицины и образовательных проектов. Одним из наиболее популярных промышленных решений является робот SCARA (Selective Compliance Assembly Robot Arm), который сочетает в себе ряд преимуществ, таких как

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №7 2025 высокая скорость, точность и достаточно простая кинематическая структура, благодаря которой они находят широкое применение в операциях по захвату и перемещению различных объектов, например, сборке промышленных изделий, упаковке и других манипуляционных задачах [1, 3].

При этом одним из важных этапов разработки и внедрения роботизированных систем в производство становится виртуальное моделирование, которое позволяет отлаживать алгоритмы управления без необходимости дорогостоящего прототипирования и рисков повреждения реального оборудования [6, 8]. Для этих целей используются как специализированные программные платформы, например, Gazebo, Webots, MATLAB/Simulink, так и программные решения собственной разработки. Среди последних своими доступностью, мощными средствами визуализации, гибкостью и растущим набором инструментов для робототехники выделяется игровой движок Unity. Результаты работы могут применяться как в образовательных целях, в частности при изучении дисциплины «Роботизация производства» в Ошском Государственном Университете (ОшГУ), так и на практике для отладки тестирования алгоритмов управления перед их загрузкой на реальный робот.

Подготовка 3D-модели и организация кинематической структуры. Для моделирования робота в программной среде Unity требуется наличие трехмерной модели, которая корректно отражает его физическую и кинематическую структуру, обеспечивая возможность реалистичного воспроизведения движения и работы робота. Существуют два основных подхода по реализации трехмерных моделей роботов: самостоятельное проектирование модели в CAD системе и использование готовых моделей, которые часто предоставляются производителем роботов. При наличии необходимых технических данных и требований к конструкции робота, проектирование модели может производиться в одной из популярных CAD систем, к которым относятся, в частности, Autodesk Fusion 360, SolidWorks и FreeCAD. При этом проектируемая модель должна учитывать геометрические параметры звеньев, их оси вращения и допустимые диапазоны движения, обеспечивая соответствие типовой конфигурации реального робота. Альтернативой самостоятельному проектированию может быть использование готовых CAD-моделей, размещенных в открытых инженерных библиотеках (GrabCAD, Thingiverse и др.) или предоставляемых производителями промышленных роботов в открытом доступе. При выборе подобной модели следует убедиться в её достаточной детализации, также в соответствии габаритов и конструкции техническим требованиям. После подготовки трёхмерной модели следующим этапом является её импорт и настройка в среде Unity. На первом этапе модель робота необходимо экспортировать из CAD-среды в один из форматов, поддерживаемых Unity, таких как .fbx, .obj или .stl. При этом, наиболее предпочтительным является формат .fbx, поскольку он позволяет сохранить иерархию объектов, трансформации, а также текстуры и материалы, применённые в CAD-среде.

Экспортированный файл помещается в папку Assets проекта Unity и автоматически отображается в обозревателе проекта. После этого модель перетаскивается на сцену для дальнейшей настройки. В окне Inspector необходимо проверить корректность масштаба и ориентацию модели. При необходимости следует привести единицы измерения CAD-системы к единицам Unity и/или выполнить поворот модели, поскольку направления систем координат в CAD и Unity могут отличаться. Кроме того, следует убедиться, что оси вращения и направления поступательного перемещения звеньев точно соответствуют кинематической структуре робота, а все опорные точки расположены в области соответствующих сочленений. Следующим этапом является организация кинематической структуры робота, для которой в Unity предусмотрено несколько способов моделирования связей между звеньями механической системы. В данной работе рассматриваются три наиболее распространённых подхода: иерархическая структура объектов (Parent-Child), использование физических соединений (Joints), а также компонент Articulation Body, предназначенный специально для задач робототехники [2].

Самым простейшим способом построения кинематической цепи является отношение родитель-потомок (Parent-Child), при котором каждое звено назначается дочерним объектом предыдущего. При таком подходе управление движением звеньев осуществляется напрямую путём изменения параметров позиции и ориентации компонента transform. Основным достоинством этого подхода является простота реализации: он не требует настройки физических свойств и позволяет интуитивно управлять положением звеньев. Однако при этом отсутствует физическая симуляция — не учитываются масса, инерция и внешние силы, что ограничивает реалистичность поведения модели.

Другой подход к моделированию связей между звеньями кинематической цепи заключается в использовании компонентов Hinge Joint или Configurable Joint, которые реализуют физические соединения с возможностью задания осей вращения, ограничений углов, жёсткости, демпфирования и других параметров взаимодействия, при этом физические свойства звеньев, такие как масса и материал, задаются через компонент твердого тела (Rigidbody). К основным преимуществам данного подхода стоит отнести возможность более реалистичного воспроизведения поведения робота с учётом силовых воздействий и моментов, однако при этом возрастает сложность настройки, увеличивается потребность в вычислительных ресурсах, в том числе за счёт необходимости повышения точности физических расчётов, а также может наблюдаться нестабильность при усложнении конфигурации механизма. Наиболее современным и функциональным способом моделирования кинематических цепей в Unity, ориентированным на задачи робототехники, является применение компонента Articulation Body, который позволяет точно настраивать параметры сочленений, включая массы, моменты инерции, диапазоны углов и типы приводов. Основным преимуществом данного подхода является высокая точность моделирования и стабильность численных расчётов, что делает его эффективным при симуляции сложных робототехнических систем. Вместе с тем компонент Articulation Body доступен только в версиях Unity 2020 и выше, и содержит ряд ограничений, в частности, не поддерживает моделирование замкнутых кинематических цепей. Таким образом, выбор метода организации связей между звеньями определяется требованиями к точности моделирования и уровню сложности решаемой задачи. В случаях, не предполагающих физического взаимодействия, допустимо использование иерархической структуры типа Parent–Child, тогда как для более точного и физически обоснованного моделирования предпочтение следует отдавать компонентам Joints или Articulation Body.

Реализация управления виртуальной моделью робота SCARA. На этапе реализации управления виртуальной моделью основное внимание уделяется обеспечению возможности управления положением и движением звеньев SCARA-манипулятора, как в ручном режиме, так и с использованием алгоритмов решения задач прямой и обратной кинематики. Управление может быть реализовано как напрямую через пользовательский интерфейс или устройства ввода (например, клавиатура или джойстик), так и программно, путём расчёта требуемых параметров движения на основе математических моделей [5].

В настоящей работе рассмотрено два способа управления роботом: ручное управление, при котором оператор непосредственно задаёт значения углов поворота вращательных звеньев и величины линейного перемещения вдоль осей поступательных звеньев, и автоматическое управление, реализуемое через решение обратной задачи кинематики, которое позволяет определение требуемых углов поворота звеньев по заданным координатам рабочего органа. Для целей тестирования и отладки виртуальной модели SCARA-робота реализована возможность управления звеньями в интерактивном режиме. Управление может осуществляться с использованием различных средств ввода, включая клавиатуру, графический интерфейс пользователя и внешние устройства, такие как джойстики. При управлении с клавиатуры изменение углов вращения звеньев осуществляется пошагово, что позволяет оперативно проверять корректность работы сочленений и соблюдение кинематических ограничений. Графический интерфейс на базе встроенных элементов UI обеспечивает наглядность и удобство взаимодействия, особенно в образовательных или демонстрационных сценариях. Использование внешних устройств ввода, таких как геймпады или трекеры, реализуется с помощью встроенных средств Unity и позволяет расширить возможности управления моделью в интерактивной среде. Ниже, в листинге 1, приведена обобщённая структура реализации ручного управления с использованием C#-скрипта в Unity:

void Update() {

ApplyJointRotation(theta1, theta2);

}

Листинг 1. Пример кода ручного управления звеньями робота в общем случае

При этом метод ApplyJointRotation() реализуется в зависимости от способа организации звеньев (см. ниже) и отвечает за физическую или трансформационную установку новых значений. Реализация управления звеньями напрямую связана с выбранным способом моделирования звеньев, описанными выше. В случае организации звеньев при помощи отношения родитель-потомок ( Parent-Child ) управление реализуется при помощи изменения локального поворота или линейного перемещения соответствующего звена, в зависимости от его типа, так как показано в Листинге 2.

Листинг 2. Пример кода управления звеньями, связанных отношением родитель-потомок

Как было отмечено выше такой подход достаточно просто реализуется, однако не может применяться в задачах, в которых необходимо учитывать силы и моменты. При организации соединений звеньев с применением компонентов Hinge Joint / Configurable Joint , управление производиться путем задания свойств физического мотора (Листинг 3), а также величин массы и типов материалов звеньев.

Также, при таком подходе, в случае необходимости можно жёстко задавать углы через параметры пружины ( spring ) и целевого положения ( target position ).

Наиболее точным и универсальным способом соединения звеньев, который поддерживает полный набор физических параметров, таких как инерция, жёсткость, трение и др., является применение компонента Articulation Body . В этом случае управление осуществляется путем установки целевого положения ( Target Position ) так, как показано в Листинге 4.

Листинг 3. Пример кода управления звеньями, связанных компонентами Hinge Joint / Configurable Joint

Листинг 4. Пример кода управления звеньями, связанных компонентами Articulation Body

Дальнейшее управление виртуальной моделью робота SCARA осуществляется посредством решения задач прямой и обратной кинематики [3-7]. Прямая задача кинематики заключается в определении положения и ориентации рабочего органа робота на основании заданных углов поворота его сочленений. Применительно к роботу SCARA, эта задача сводится к вычислению координат рабочего органа (эффектора) на основе известных углов и длин звеньев манипулятора. Иными словами, при заданных значениях углов сочленений можно легко и однозначно определить, где именно будет находиться рабочий орган робота. Обратная же задача кинематики, напротив, решает вопрос о том, как именно нужно расположить звенья робота, чтобы рабочий орган занял заданное положение в пространстве. Необходимо отметить, что на практике обратная задача кинематики является более востребованной и имеет большую значимость в роботизированных системах. Однако эта задача редко имеет единственное решение. В частности, для заданного набора углов сочленений ( Q 1 , Q 2 , …, Q n ) всегда можно однозначно определить положение рабочего органа ( x, y, z ), но обратное утверждение справедливо не всегда. Для одной и той же точки ( x, y, z ) может существовать несколько различных наборов углов ( Q 1 ' , Q 2 ' , …, Q n ' ). Это обусловлено математической спецификой задачи, где решения часто выражаются через многочлены и квадратные корни, что порождает множественность решений [8].

Для более детального понимания рассмотрим пример решения прямой задачи кинематики для плоского двухзвенного манипулятора, представленного на Рисунке 1. На рисунке изображён упрощенный манипулятор SCARA, работающий в одной плоскости и состоящий из двух вращательных звеньев: плеча ( L 1 ) и локтя ( L 2 ). Первый сустав закреплён на основании и вращается на угол Q 1 относительно горизонтальной оси. Второе звено крепится к концу первого и совершает вращение на угол Q 2 относительно первого звена. Эффектор расположен на конце второго звена. Прямая задача кинематики формулируется следующим образом: зная длины звеньев ( L 1 , L 2 ) и углы вращения ( Q 1 , Q 2 ), требуется определить координаты рабочего органа ( x, y ). Формально это выражается следующими уравнениями:

x = L₁-cos(Q_l) + L₂-cos(Q_l+ Q₂]                           (1)

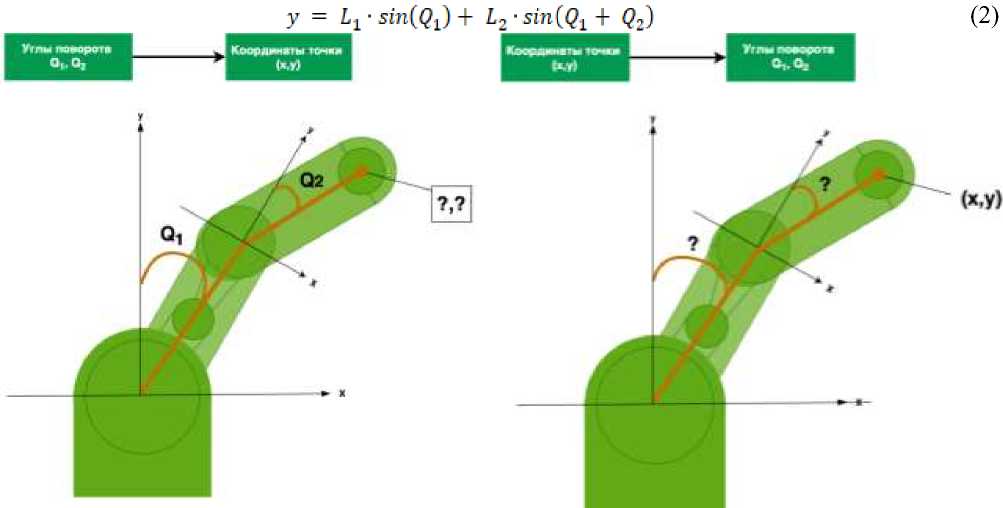
(х.У)

Коодовмггы w# м

Рисунок 1. Схема двухзвенного плоского манипулятора SCARA для иллюстрации решения задач кинематики

В листинге 5 приведен пример кода расчета прямой задачи кинематики для робота SCARA в среде Unity3D. В данном методе используются встроенные математические функции среды Unity (Mathf), а результатом выполнения функции является трёхмерный вектор, описывающий положение рабочего органа в плоскости манипулятора. Этот подход позволяет удобно интегрировать кинематические расчеты непосредственно в виртуальную среду и оперативно визуализировать результаты.

return new Vector3(x, y, 0);

}

Листинг 5. Пример кода расчета прямой задачи кинематики для робота SCARA в среде Unity3D

Обратная задача кинематики используется для определения углов звеньев, которые обеспечат заданное положение рабочего органа. Этот метод часто применяется в робототехнике, когда необходимо расположить инструмент робота в конкретных координатах ( x, y ). Для решения обратной задачи кинематики сначала рассчитывается расстояние от начала координат до заданной точки ( x, y ), обозначим его как B :

В2 = х2 + у2

Угол q 1 между осью OX и прямой B находится по формуле:

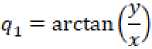
Угол q2 между прямой B и звеном L1 вычисляется по теореме косинусов:

^2

= arccos

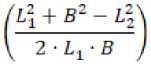
Тогда угол Q 1 рассчитывается как разность:

91 _ *71 4г

Аналогично, угол Q 2 между звеньями L 1 и L 2 также определяется по теореме косинусов:

(Ь\ + l22 -b2\

Q2 — Tt — arccos I —-----------I(7)

\ 2 •L^'L₂ у

Следует учесть, что для заданной точки (X, Y) существует альтернативная конфигурация манипулятора, когда:

91 =41 + 42(8)

9г = ~9з(9)

Таким образом, при расчете обратной задачи кинематики всегда необходимо учитывать возможность неоднозначности решения. Пример кода расчета обратной задачи кинематики в Unity3D приведен в листинге 6. В приведенном листинге кода метод CalculateInverseKinematics принимает на вход длины звеньев ( L 1 , L 2 ) и координаты целевой точки, а дополнительный параметр elbowUp позволяет выбрать конфигурацию манипулятора: «локоть вверх» или «локоть вниз». Стоит отметить, что рассмотренные формулы прямой и обратной задач кинематики применимы для упрощенной плоской модели манипулятора SCARA, работающей в одной плоскости ( XY ). В реальных задачах для робота SCARA дополнительно задаётся вертикальное линейное перемещение рабочего органа по оси Z , которое обычно регулируется независимо от вращательных степеней свободы и рассчитывается отдельно.

public bool CalculateInverseKinematics(float L1, float L2, Vector2 target, out float Q1, out float Q2, bool elbowUp = true)

{

// Вычисляем расстояние от основания манипулятора до заданной точки float B = target.magnitude;

{

// Точка находится вне зоны досягаемости манипулятора

Q1 = Q2 = 0; return false; }

// Угол q1 между осью OX и прямой, соединяющей основание с целевой точкой float q1 = Mathf.Atan2(target.y, target.x);

// Угол Q1 зависит от выбранной конфигурации (локоть вверх или вниз)

Q1 = elbowUp ? (q1 - q2) : (q1 + q2);

// Угол Q2 между плечом (L1) и локтем (L2)

return true; }

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №7 2025

Листинг 6. Пример кода расчета обратной задачи кинематики для робота SCARA в среде Unity3D

Для обеспечения плавного и реалистичного перемещения рабочего органа робота SCARA между заданными позициями, помимо расчета положений через прямую и обратную задачи кинематики, важное значение приобретает расчет траектории движения. Одним из наиболее простых и распространенных подходов является линейная интерполяция между двумя заданными точками, при которой промежуточные положения рабочего органа рассчитываются как линейная комбинация начальной и конечной позиций. Ниже, в листинге 7, приведен пример реализации линейной интерполяции в Unity3D:

Vector3 startPosition = CalculateEndEffectorPosition(L1, L2, Q1_start, Q2_start);

Vector3 endPosition = CalculateEndEffectorPosition(L1, L2, Q1_end, Q2_end);

for (float t = 0; t <= 1; t += 0.01f) {

// Визуализация текущего положения рабочего органа }

Листинг 7. Пример кода линейной интерполяции траектории движения рабочего органа

Перспективной возможностью виртуальной модели робота является её интеграция с системами числового программного управления (ЧПУ), что позволяет использовать стандартный язык программирования траекторий G-код. G-код представляет собой последовательность команд, которые определяют действия робота, такие как перемещения по заданным координатам, выбор скоростей и другие параметры работы. В рамках данной работы был разработан модуль для обработки и интерпретации G-кода в Unity3D. Базовые команды, поддерживаемыми модулем приведены в Таблице.

Таблица

БАЗОВЫЕ КОМАНДЫ G-КОДА, ПОДДЕРЖИВАЕМЫЕ

В РАЗРАБОТАННОМ ПРОГРАММНОМ ОБЕСПЕЧЕНИИ

Команда	Описание
G0/G1	Линейное перемещение рабочего органа в указанные координаты ( x, y, z ).
G90	Абсолютное позиционирование, координаты задаются относительно нулевой точки.
G91	Относительное позиционирование, координаты задаются относительно текущего положения.
F	Установка скорости перемещения рабочего органа.

Процесс обработки G-кода включает следующие этапы:

Парсинг строк G-кода из текстового файла и выделение команд и их параметров.

Преобразование выделенных координат и параметров в целевые позиции с использованием обратной задачи кинематики.

Выполнение расчетов промежуточных точек траектории с применением линейной интерполяции, обеспечивающей плавность движения робота.

Пример упрощенного алгоритма парсинга команды G-кода представлен ниже в листинге 8:

Скорость движения робота, заданная командой F в G-коде, реализуется путём изменения параметра времени или шага интерполяции между точками траектории. Чем выше заданная скорость (значение F), тем меньшее время затрачивается на прохождение каждой промежуточной точки траектории, и наоборот. В Unity это достигается регулировкой

Бюллетень науки и практики / Bulletin of Science and Practice Т. 11. №7 2025 скорости изменения параметра интерполяции (например, величиной шага t в цикле интерполяции). Таким образом, виртуальная среда позволяет предварительно отлаживать программы, предназначенные для реального оборудования, минимизируя риски возникновения ошибок и увеличивая эффективность реальной эксплуатации робота [9].

string command = "G1 X10 Y20 Z0 F1500";

float x = 0, y = 0, z = 0, speed = 0;

Листинг 8. Пример кода парсинга команды G-кода

Поддержка G-кода существенно расширяет область применения созданной модели и позволяет более гибко подходить к решению различных производственных задач. В рамках настоящей работы авторами была разработана демонстрационная программа в среде Unity3D, реализующая описанные выше алгоритмы. Приложение позволяет интерактивно изменять значения углов звеньев и координаты рабочего органа, визуализируя расчеты прямой и обратной задач кинематики в реальном времени. На Рисунке 2 представлен скриншот интерфейса Unity c демонстрационной программы по управлению роботом SCARA.

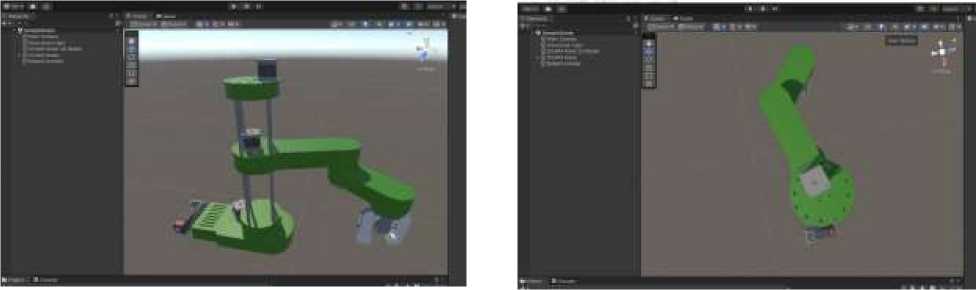
Рисунок 2. Скриншот разработанной демонстрационной программы по управлению роботом

SCARA в Unity3D

Разработанная виртуальная модель робота SCARA имеет значительный потенциал для дальнейшего развития. К перспективным направлениям можно отнести:

Стоит отметить, что роботы типа SCARA часто используются для автоматизации типовых задач, таких как сборка, перемещение и упаковка, что делает их востребованными на производстве. Поэтому, использование разработанной виртуальной модели, позволяет студентам на практике изучить принципы работы и управления промышленными роботами, без рисков и затрат, связанных с эксплуатацией реального оборудования.

Итак, представлены основные этапы разработки виртуальной модели робота SCARA в среде Unity3D, включающие подготовку и настройку 3D-модели, организацию кинематической структуры, реализацию базовых алгоритмов управления с решением прямой и обратной задач кинематики, а также построение траекторий движения с использованием программирования на основе G-кода [12-17].

Проведённые исследования подтвердили удобство и эффективность применения среды Unity3D для задач виртуального моделирования и отладки алгоритмов управления роботизированными системами, что открывает широкие перспективы как для образовательных целей, так и для практических приложений в робототехнике. Практическая значимость работы состоит в её образовательном применении, а также в возможности проведения предварительного тестирования и оптимизации алгоритмов управления перед их внедрением в реальное производство.