Визуализация численного решения волнового уравнения

Рассмотрим двумерную краевую задачу, содержащую волновое уравнение:

9²u(x, y, t) dt²

(92u(x,y,t)  92u(x,y,t)\

= v2 ---+--- (1).

у   ox2          oy2   /

Где v — фазовая скорость распространения волн.

x е [0, а], у е [0, Ь].

u(x,y, 0) = /(x,y) — Начальные условия.

u(x,y, t) = p.(x,y, t) — Граничные условия, где x,y —

точки границы исследуемой области.

Для получения численного решения разобьем исследуемую область на одинаковые ячейки таким образом, чтобы по ширине их помещалось ровно w штук и Л штук по высоте. Это позволяет перейти к новым координатам, в которых доступ к каждой ячейке происходит по индексу, а область представима в виде двумерного массива (см. рисунок 1).

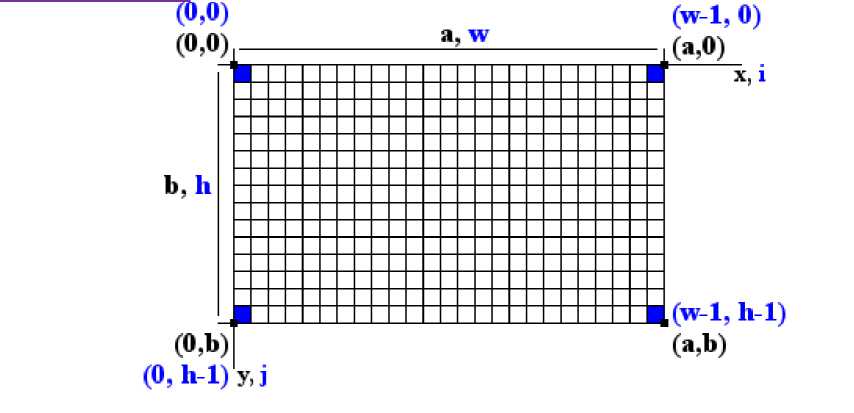
Рисунок 1. Переход к дискретным координатам.

x ^ i, y^j, t ^ т, u(x,y,t) ^ u(i,j,T).

Значения функции u в таких ячейках и будет являться приближенным решением поставленной задачи.

Выберем простое граничное условие ^ = 0, которое характеризует закрепление концов области в нулевом положении. В нашей задаче это означает полное отражение волн от границы.

Теперь запишем разностные схемы, необходимые для аппроксимации производных в уравнении (1):

d²u(x, y, t) dt²

d2u(x, y, t) dx2

d2u(x, y, t) dy2

u(x, y,t — dt) — 2u(x, y, t) + u(x, y,t + dt)

+ O(dt2).

dt2

u(x — dx, y, t) — 2u(x, y, t) + u(x + dx, y, t)

—----—----t^-------— + 0(dx2).

dx2

u(x, y — dy, t) — 2u(x, y, t) + u(x, y + dy, t)

-------------------dy^-------------------+ O(dy2).

Где dt — шаг по времени,

dx — шаг по координате x, dy — шаг по координате у.

Выражения O(dt2), O(dx2), O(dy2) характеризуют второй порядок точности аппроксимации производных.

В дискретной системе координат выражения для аппроксимации производных примут вид:

d²(x, y, t) dt²

u(i,j, т — 1) — 2u(i, j, т) + u(i,j, т + 1)  (2.1).

d2u(x, y, t) dx2

« u(i — 1,j,r) — 2u(i,j,т) + u(i + 1,j, т)

(2.2).

d2u(x, y, t) dy2

« u(i,j — 1,т) —

2u(i,j,т) + u(i,j + 1,т)

(2.3).

Заметим, что при таком подходе время также является дискретной величиной. Из (2.1) видно, что необходимо обладать сведениями хотя бы о двух предыдущих состояниях системы, чтобы узнать ее состояние в последующий момент времени.

Информацию о первых двух состояниях несут начальные условия:

u(i,j,0) = f(i,j).

u(i,j, 1) = f(i,jy

Подставим выражения (2.1), (2.2) и (2.3) в уравнение (1):

u(i,j, т — 1) — 2u(i,j, т) + u(i,j, т + 1) = v2 (u(i — 1,j, т) — 2u(i, j, т) + +u(i + 1,j, т) + u(i,j — 1,т) — 2u(i,j,т) + u(i,j + 1,т)).

И приведем подобные

u(i,j, т + 1) = v2 (u(i — 1,j, т) + u(i + 1,j, т) + u(i,j — 1, т) +

+ u(i,j + 1, т)) + u(i,j, т)(2 — 4v2) — u(i,j, т — 1)  (3).

Полученное выражение и будем использовать для пересчета значений функции и в каждой клетке, кроме граничных, для следующего момента времени на основании двух предыдущих (явный метод).

Все расчеты и визуализацию целесообразно производить при помощи современных ЭВМ. Стоит отметить, что при таком подходе нет необходимости хранить в памяти больше трех состояний системы как этого требуют некоторые другие методы.

Ниже представлены примеры выполнения алгоритма, для различных начальных условий.

Если в середину области поместить ячейку со значением 1, то для различных т можно наблюдать следующую картину:

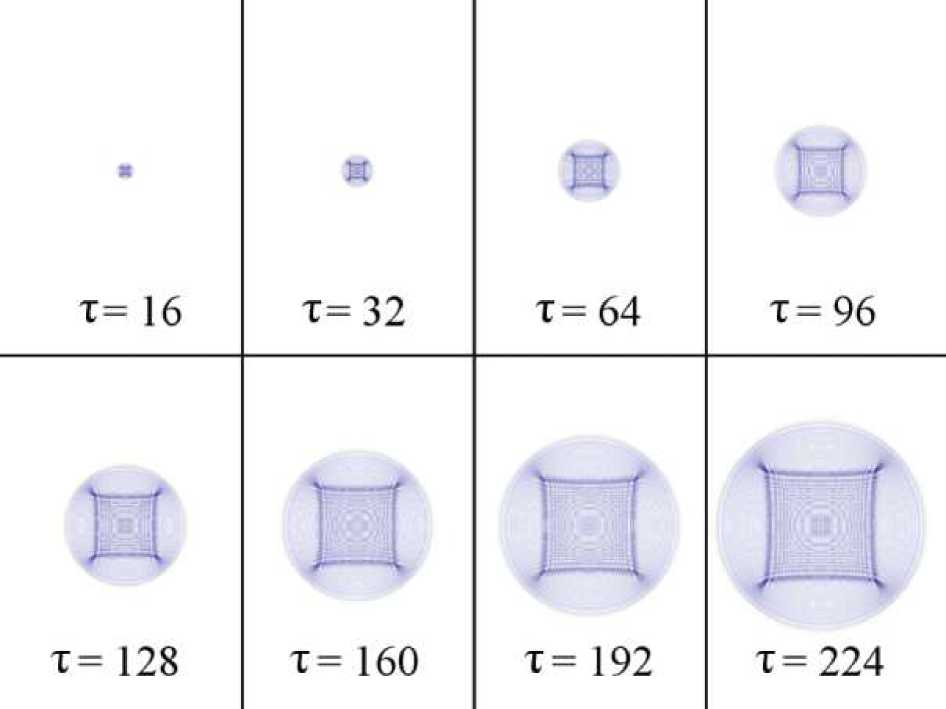
Рисунок 2. Распространение одиночной сферической волны при а? = 0,25.

Здесь черным цветом отображаются положительные значения функции и, синим – отрицательные, белым – нуль.

Интенсивность цвета нормируется по максимальному и минимальному значениям для данного значения т таким образом, что наиболее большим по модулю значениям соответствовал наиболее интенсивный цвет. Без такой нормировки в связи с рассеиванием величины и все цвета побледнеют, и картина потеряет информативность.

Рисунок 3. Чередование положительных и отрицательных гребней волны.

Если применить фильтр, который отображает все положительные значения функции и черным, все отрицательные - синим, то получим картину, которую можно наблюдать на рисунке 3.

Здесь хорошо видно чередование положительных и отрицательных гребней волны.

Если мы хотим потребовать физичности результата, а именно w—1 H—1

w—1 H—1

S(t) = IIu(i,j, t) = IIu(i,j, 0) = const, Vt

1=0 j=0

1=0 j=0

То есть выполнения закона сохранения величины и в бездивергентном поле, то необходимо выбрать, какие значения может принимать параметр b = п².

min(b) = 0 — естественный выбор нижней границы модуля скорости, когда нет распространения.

И max(b) = 0,5 — значение из выражения (3), которое не меняет знак при u(i,j,T).

Именно в таких пределах b £ [0,0.5] и выполняется условие (4).

При других значениях этого параметра сумма S перестает быть постоянной, а ее модуль начинает экспоненциально возрастать.

Кроме того, вид, который принимает процесс, перестает быть похожим на колебательный.

Другими словами, мы получили критерий устойчивости схемы.

Удобство численного решения заключается в первую очередь в том, что можно применять начальные и граничные условия любой сложности, и для каждого нового случая не придется решать отдельную задачу. К тому же в нашем случае мы можем визуально наблюдать решение и корректировать начальные и граничные условия в случае необходимости.