Визуализация движения мехатронно-модульного робота

Введение. Разработка модульных роботов (МР) с адаптивной кинематической структурой в настоящее время является одним из перспективных направлений мехатроники. МР состоят из однотипных модулей, объединенных в единую многозвенную конструкцию, а соединение таких модулей позволяет создавать различные по структуре механизмы. По сравнению с обычными мобильными роботами МР обладают серьезными преимуществами, среди которых надежность и способность преодолевать сложные препятствия. В МР используются новейшие достижения робототехники, мехатроники, теории управления (в том числе интеллектуальное управление движением). Одна из основных областей применения МР – экстремальная робототехника [1]. К сожалению, в литературе практически отсутствует информация о внутренней структуре, алгоритмах и программном обеспечении, используемых для управления перемещением и реконфигурацией таких роботов. Из отечественных работ следует упомянуть статью [2], в которой рассмотрено движение одномерного МР по плоской поверхности.

Разработка кинематической схемы и программа визуализации. Нами исследована визуализация волнообразного взаимного смещения модулей МР, приводящего к его продольному пере- мещению. Приняты следующие допущения и ограничения: все модули имеют одинаковые геомет-

Рис.1. Стадии цикла одного перемещения МР

рические размеры; каждый из модулей состоит из головного и хвостового звеньев одинаковой длины и бесконечной жесткости; звенья соединены безлюфтовым шарниром с одной степенью подвижности, допускающим их взаимный поворот на угол ±(π–γ). Угол γ определяется конструктивными ограничениями используемых в модулях МР шарниров. Начало неподвижной декартовой системы координат связано с начальным положением «кончика хвоста» первого модуля. Направление оси OX совпадает с направлением движения МР. Ось OY повернута относительно оси OX на угол π/2 против часовой стрелки (на рис.1 оси координат не показаны). Звенья каждого модуля условно обозначены отрезками прямых: черными – для голов- ного, т.е. первого по направлению движения МР, белыми – для хвостового звеньев (см. рис.1, на котором показана последовательность прохождения волны по длине модуля). Номера модулей обозначены цифрами у соответствующих шарниров. Звенья каждого i-го модуля образуют между собой углы αi, где i – порядковый номер модуля, начиная с крайнего левого.

На примере МР, состоящего из n =5 последовательно соединенных модулей, составлена кинематическая модель. Анализ кинематики движения МР позволил составить уравнения, описывающие изменения углов при вершинах модулей в зависимости от времени. Обозначив длину одного звена модуля через l , запишем выражение для максимально допустимого перем ещения МР за один цикл движения как Δ x _max = 2 l (2 - 2(1 - cos γ )) (величина Δ x _max ограничивается параметром γ ). Угол α i , при котором будет обеспечено заданное перемещение ∆ х (например, при вершине модуля 2 на рис.1, стадия б ), составит:

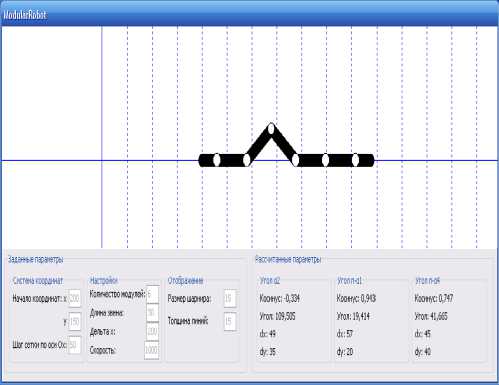
Рис.2. Интерфейс программы «ModularRobot»

8l∆x-8l2-(∆x)2 α = arccos.

При прохождении волны по длине робота угол при шарнире модуля 2 проходит через значение α 2 =π

(см. рис.1, стадия в), которому соответствуют значения углов при шарнирах 1 и 4: 48l2 -12l∆x+ (∆x)2 α = arccos

• ¹               8 l ( ∆ x - 6 l )

  α ₄ = arccos

  
  

24 l ² - 12 l ∆ x + ( ∆ x )² 4 l ∆ x - 24 l ²

Перемещение МР обеспечивается за счет последовательного воспроизведения повторяющихся движений всеми модулями МР как элементами кинематической цепи, в результате чего от первого модуля к последнему «пробегает» волна и весь МР продвигается вперед на расстояние Δ x . Задачей системы управления перемещением робота является согласованная отработка углов в шарнирах модулей. На основе кинематической модели разработана программа «ModularRobot» (рис.2), позволяющая визуализировать перемещение МР при последовательном выполнении движений каждым звеном, что в дальнейшем будет использовано при отработке интеллектуальной системы управления движением таких роботов. Визуализация может быть реализована в любом назначенном оператором масштабе времени.

Заключение. В результате проведенных исследований разработана кинематическая модель многозвенного модульного робота и программа визуализации его движения. Полученные результаты могут быть использованы при разработке интеллектуальной системы управления движением и реконфигурацией модульных роботов в условиях неопределенности внешней среды.