Визуализация на занятиях по математике

математика является наиболее абстрактной. В ходе нашего исследования мы попытались ответить на следующие вопросы:

• 1)    какие преимущества имеет визуализация для обучения математике?

• 2)    какие модели визуализации используются на уроках математики?

П. Гретш и Л. Хольцапфель рассматривают следующие модели визуализации информации (также их называют информационными):

• •    вербальная (словесное или текстовое описание);

• •    графическая (график, чертеж, схема);

• •    математическая (описание формулами);

• •    табличная (объект-объект, объект-свойство).

Визуализация учебной информации подразумевает необходимость применения моделей в преподава- нии, поскольку они подчеркивают определенную информацию о соответствующем объекте [6, с. 91].

Рассмотрим, какие действия можно проделать при переходе с одной модели на другую на примере изучения темы «Линейная функция» (табл.).

Некоторые переходы между информационными моделями для учащихся средней школы будут сложны для представления и применения. Каждая из моделей визуализации информации может трактоваться неоднозначно, в зависимости от ситуации и преследуемых целей. Иногда поставленная проблема воспринимается как математическая формула, иногда – как график на координатной плоскости. В отдельных случаях формула предстает и в виде графика, и в виде текста. Таким образом, переход между моделями представляет со- бой не что иное, как установление связи между графиком, математической формулой или таблицей и др. Поэтому на сегодняшний день разработан ряд различных программ, направленных на визуализацию математических формул для восприятия учебной информации. Если до сих пор при изучении математики все сводилось к поиску решения «ручкой» на бумаге, то использование этих программ позволяет осуществить проверку решения, справляться с новыми и более близкими к реальной жизни заданиями.

Нередки ситуации, когда учитель доходчиво рассказывает и объясняет, а учащиеся смотрят, слушают, но не воспринимают. Возможно, у них нет прочной базы или они не владеют «языком» математики, чтобы анализировать и преобразовывать учебную информацию. Точные критерии того, что ученик не только знает материал, но и понимает его, отсутствуют. Именно поэтому смена моделей во время преподавания в большинстве случаев бывает необходима.

Требование для учащихся понимать и проявлять самостоятельность при введении в теоретическую часть учебной информации обычно ослабляется в средней школе, так как иногда теоремы и определения предлагаются для принятия к сведению, а не для их вовлечения в мыслительный процесс. Используя готовый теоретический материал, учащиеся не принимают во внимание тот факт, что его нужно описать и интерпретировать. В большинстве случаев это практически невозможно из-за отсутствия навыков пере-

Действия при переходе между информационными моделями

Переходы с/на Вербальная Графическая Табличная Математическая Вербальная Переформулировать определение Начертить график Найти значение Описать математические формулы Графическая Интерпретировать график Изменить график на координатной плоскости Считать информацию с графика Представить приблизительную функцию Табличная Прочитать значения в таблице Внести точки на график Найти следующие значения функции Вычислить приблизительную функцию (регрессия) Математическая Интерпретировать формулу Начертить график Вычислить значения Переформулировать математически хода с математической на графическую и вербальную модели и наоборот во время изучения учебной информации. Рассмотрим некоторые из возможных вариантов перехода между графической и вербальной информационными моделями на примере доказательства из учебника по геометрии [5, с. 182].

Теорема . В любой треугольник можно вписать окружность.

Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой O точку пересечения его биссектрис. Проведем из точки O перпендикуляры OK , OL и OM соответственно к сторонам AB , BC и CA . Так как точка O равноудалена от сторон треугольника ABC , то OK = OL = OM . Поэтому окружность с центром O радиуса OK проходит через точки K , L , M . Стороны треугольника ABC касаются этой окружности в точках K , L , M , так как они перпендикулярны радиусам OK , OL и OM . Значит, окружность с центром O радиусом OK является вписанной в треугольник ABC .

Объем доказательства затрудняет его понимание и восприятие, чтобы было возможно делать какие-то выводы. Представление доказательства в виде чертежа позволяет учащимся объединить отдельные положения доказательства в целостную картину, выделить стандартные образы и прийти к правильному решению.

Е.И. Барановская пишет: «Выполняя чертеж (рисунок), стремитесь сделать его соответствующим условию задачи. Хороший чертеж – это удобный для восприятия наглядный способ записи условия задачи, он может стать помощником в решении задач, подсказать правильный ход рассуждений. В то же время надо отчетливо понимать, что даже самый аккуратный, выполненный с помощью циркуля и линейки чертеж сам по себе ничего не доказывает. Все, что увидено на чертеже, должно быть обосновано соответствующим логическим выводом» [2]. Чтобы воспринять содержание в вербальном описании математических формул или геометриче-

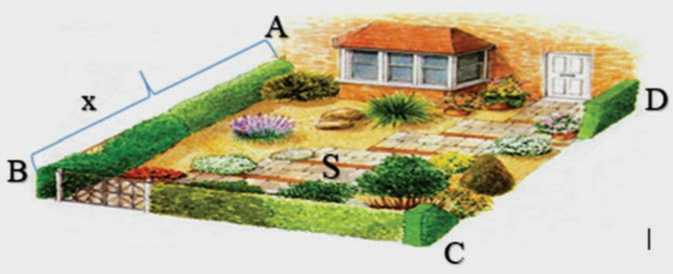
Графическая модель визуализации задачи

ских объектов, учащимся необходимо: 1) иметь запас различных образов, то есть знать их визуальное представление, и далее 2) на основе накопленных знаний прийти к логическому обоснованию и интерпретации этих объектов. Способность к одной и той же математической формуле применять разные информационные модели, по сути, является центральным фактором математического понимания.

На данный момент разработано учебное пособие с компьютерной поддержкой. Главная цель пособия – визуализация геометрических объектов, формирование у детей практических навыков применения геометрических знаний. Наблюдая за изменениями геометрических объектов, учащиеся могут находить некие закономерности, интерпретировать и учиться решать задачи. При этом необходимо помнить, что одно только использование графических моделей для визуализации геометрических объектов не является содержательно значимым, если учащиеся не могут применить к этому математическое объяснение, осуществить переход с графической модели на математическую.

Привитие учащимся навыков построения перехода между моделями, восприятия информации графически, вербально или математически позволяет преодолеть проблемы, возникающие у них при изучении математики.

Рассмотрим переход между вербальной, графической и математической моделями. В качестве ус- ловия задачи предлагается проблемная ситуация из повседневной жизни, к которой учащимся нужно подойти с использованием формулы для вычисления вершины параболы.

Задача . Необходимо огородить стену дома забором длиной 40 метров. Какая длина должна быть у сторон прямоугольника, чтобы забор мог охватить максимальную площадь?

Решение . Длина забора 40 метров. Ставить забор на стену дома нет необходимости.

Длину AB и CD мы определяем неизвестной x . Так как длина забора составляет 40 м, то 40 – 2 x является длиной BC . Тогда площадь, охватываемая забором, будет составлять S = x ⋅ (40 – 2 x ) = 40 x – 2 x ². Мы имеем квадратичную функцию, где с помощью формулы вычисления вершины параболы можем определить координаты x и S , тогда

–40

x = _{2 ⋅ (–2)} = 10

и

S =

4■(-2)■ 0 - 402 4■(-2)

= 200.

Если вершины квадратичной функции находятся в точке с координатами (10; 200), то для неизвестной x = 10 м, площадь забора будет максимальной S = 200 м², а это значит, что ширина забора AB = CD = 10 м и длина забора BC = 40 – 2 ⋅ 10 = 20 м. Соответственно, и длина дома будет равна 20 м.

Данная задача начинается с вербального описания ситуации, далее она проиллюстрирована на рисунке, где определяются неизвестные, для нахождения которых применяются математические формулы. В данном случае используются три модели, которые учащиеся должны не только освоить, но также построить связь между ними: 1) вербальная модель в текстовом виде, 2) графическая модель в виде рисунка и определения прямоугольника и 3) математическая модель в виде формул и расчетов. Рисунок позволяет охватить проблему «в целом», выделить неизвестные стороны для построения хода решения задачи. Геометрическая интерпретация применяется для демонстрации содержания поставленной задачи, однако на самом деле ее роль многограннее.

Американский исследователь М. Иден сформулировал свойство визуальной информации: «Она достаточно устойчива и является своим собственным визуальным представлением и позволяет людям обмениваться с помощью зрительных образов по существу той же информацией, которой они могли бы обменяться в устной речи» [4, с. 280].

Целью данной работы было показать важность визуализации в обучении математике и необходимость построения связи между информационными моделями для преподавания и изучения математики. Визуализация в формате графических представлений информации может помочь понять идею и процесс обучения учащихся и послужить поводом для более важных дискуссий и размышлений.

На занятиях учащиеся часто встречаются с функциями в вербальном, графическом, табличном или математическом представлении, каждое из которых сфокусировано на определенном явлении, поэтому важно понимать переход с одной модели на другую. Необходимые действия, которые должны быть выполнены при переходе между моделями, описаны в табл. (см. выше). На основе этих действий учащимся можно представлять учебную информацию. Целенаправленная практика переходов между моделями визуализации информации содействует тому, что учащиеся лучше распознают необходимые признаки в учебной информации.