Визуальное представление многомерных задач линейного программирования
Автор: Ольховский Николай Александрович, Соколинский Леонид Борисович
Статья в выпуске: 1 т.11, 2022 года.
Бесплатный доступ
В статье строится n-мерная математическая модель визуального представления задачи линейного программирования. Эта модель позволит использовать аппарат искусственных нейронных сетей для решения многомерных задач линейной оптимизации, допустимая область которых является ограниченным непустым множеством. Для визуализации задачи линейного программирования вводится целевая гиперплоскость, ориентация которой определяется градиентом линейной целевой функции: градиент является нормалью к целевой гиперплоскости. В случае поиска максимума целевая гиперплоскость располагается таким образом, чтобы значение целевой функции во всех ее точках превосходило значение целевой функции во всех точках допустимой области, представляющей собой ограниченный выпуклый многогранник. Для произвольной точки целевой гиперплоскости определяется целевая проекция на многогранник: чем ближе точка целевой проекции к целевой гиперплоскости, тем больше значение целевой функции в этой точке. На основе целевой гиперплоскости строится конечное регулярное множество точек, называемое рецептивным полем. С помощью целевых проекций строится образ многогранника, включающий в себя точки рецептивного поля и расстояния до соответствующих точек поверхности многогранника. На основе предложенной модели строится параллельный алгоритм визуализации задачи линейного программирования. Дается аналитическая оценка его масштабируемости. Приводятся сведения о программной реализации и результаты масштабных вычислительных экспериментов, подтверждающие эффективность предложенных подходов.
Линейное программирование, n-мерная визуализация, математическая модель, параллельный алгоритм, bsf-каркас
Короткий адрес: https://sciup.org/147237442
IDR: 147237442 | УДК: 004.032.26
Текст научной статьи Визуальное представление многомерных задач линейного программирования
Быстрое развитие технологий накопления и обработки больших данных [1, 2] привело к появлению оптимизационных математических моделей в виде сверхбольших задач линейного программирования (ЛП) [3] . Такие задачи возникают в индустрии, экономике, логистике, статистике, квантовой физике и других областях [4 —8] . Классическое программное обеспечение во многих случаях не позволяет решить подобные масштабные задачи ЛП за приемлемое время [9] . Вместе с тем в ближайшие 2–3 года появятся вычислительные системы экзафлопсного уровня производительности [10] , потенциально способные решать подобные задачи. В соответствии с этим актуальной является задача разработки новых эффективных методов для решения сверхбольших задач ЛП с помощью экзамасштабных вычислительных систем.
До настоящего времени одним из самых распространенных способов решения задачи ЛП являлся класс алгоритмов, предложенных и разработанных Данцигом на основе симплекс-метода [11]. Симплекс-метод оказался эффективным для решения большого клас- са задач ЛП. Однако симплекс-метод имеет некоторые фундаментальные особенности, ограничивающие его применение для больших задач ЛП. Во-первых, в определенных случаях симплекс-методу приходится перебирать все вершины симплекса, что соответствует экспоненциальной временной сложности [12]. Во-вторых, симплекс-метод в большинстве случаев удовлетворительно решает задачи ЛП, содержащие до 50000 переменных, однако на больших задачах часто наблюдается потеря точности, которая не может быть компенсирована даже путем применения таких ресурсоемких процедур, как «аффинное масштабирование» или «итерационное уточнение» [13]. В-третьих, в общем случае симплекс метод плохо масштабируется на многопроцессорных системах с распределенной памятью. Были предприняты многочисленные попытки построить масштабируемую реализацию симплекс-метода, однако они не увенчались успехом [14]. Кармаркар предложил метод внутренних точек [15], способный решать сверхбольшие задачи ЛП с миллионами переменных и миллионами уравнений [16]. Более того, алгоритмы, основанные на методе внутренних точек, являются самокорректирующимися, и поэтому обеспечивают высокую точность вычислений. В качестве недостатка метода внутренних точек следует отметить тот факт, что для начала работы алгоритма необходимо иметь точку, удовлетворяющую всем ограничениям задачи ЛП. Нахождение такой внутренней точки может сводиться к решению дополнительной задачи ЛП. В качестве альтернативы можно указать метод псевдопроекций, основанный на использовании фейеровских отображений [17]. Еще одним существенным недостатком метода внутренних точек является его плохая масштабируемость применительно к многопроцессорным системам с распределенной памятью. Было сделано несколько попыток построить параллельную реализацию для частных случаев (см., например, [18, 19]), но эффективную параллельную реализацию для экзамасштабных многопроцессорных систем в общем случае построить не удалось. В соответствии с этим является актуальным направление исследований, связанное с поиском новых масштабируемых методов решения задач ЛП.
Возможной эффективной альтернативой классическим методам ЛП являются методы оптимизации, основанные на нейросетевых технологиях. Искусственные нейронные сети [20, 21] являются одним из самых обещающих и быстро развивающихся направлений современных информационных технологий. Нейронные сети представляют собой универсальный инструмент, способный решать задачи практически во всех областях. Особенно большие успехи достигнуты в распознавании и анализе изображений с помощью сверточных нейронных сетей [22] . Однако, в научной периодике практически отсутствуют работы, посвященные применению сверточных нейронных сетей для решения задач линейной оптимизации [23] . Это связано с тем, что сверточные нейронные сети ориентированы на распознавание и анализ изображений, но в научной литературе отсутствуют работы по визуальному представлению многомерных задач линейного программирования. Таким образом, вопрос разработки новых нейросетевых моделей и методов применительно к линейной оптимизации остается открытым.
В этой статье мы предприняли попытку построить n -мерную математическую модель визуального представления задачи ЛП, которая позволит использовать аппарат искусственных нейронных сетей для решения многомерных задач линейной оптимизации, допустимая область которых является ограниченным непустым множеством. Метод визуализации, основанный на описываемой модели, обладает высокой вычислительной сложностью. Поэтому мы предлагаем его реализацию в виде параллельного алгоритма, ориентированного на кластерные вычислительные системы. Статья организована следующим образом. Раз- дел 1 посвящен построению математической модели визуального представления многомерной задачи ЛП. В разделе 2 описывается реализация предложенного метода визуализации в виде параллельного алгоритма и дается аналитическая оценка его масштабируемости. В разделе 3 приводится информация о программной реализации описанного параллельного алгоритма и обсуждаются результаты масштабных вычислительных экспериментов на кластерной вычислительной системе. В заключении суммируются полученные результаты и приводятся направления дальнейших исследований.
1. Математическая модель визуального представления задачи ЛП
Рассмотрим задачу ЛП в следующей форме:
x = argmax {(c,x)|Ax < b, x G Rn} , где c,b E Rn, A E Rmxn и c = 0. Здесь langlecdot, cdotrangle обозначает скалярное произведениедвух векторов. Мы предполагаем, что ограничение x \geqslant \bfzero также включено в систему Ax \leqslant b виде неравенств
-
—xi + 0 + ......... + 0 ^
0 — X 2 + 0 + ••• + 0 < 0;
0 + ......... + 0 — xn ^
Вектор c является градиентом линейной целевой функции f (x) = C1X1 + . . . + CnXn.
Обозначим через M допустимую область задачи (1) :
M = {x G Rn|Ax ^ b} .
Везде далее мы предполагаем, что M является непустым ограниченным множеством. Это означает, что M представляет собой выпуклый замкнутый многогранник в пространстве \BbbR n , и множество решений задачи (1) не является пустым.
Пусть a i G R n — вектор, образованный элементами i -той строки матрицы A. Тогда матричное неравенство Ax \leqslant b можно представить в виде системы неравенств
(ai, x) ^ bi,i = 1,..., m.
Везде далее мы будем предполагать, что для всех i = 1,..., m ai = 0.
Обозначим через H i гиперплоскость, задаваемую уравнением
(ai,x) = bi (1 < i < m).
Таким образом,
Hi = {x G Rn|(ai,x) = bi} .
Определение 1. Под полупространством H + , порождаемым гиперплоскостью H i , будем понимать полупространство, определяемое формулой
H + = { x g R n |< a i ,x > ^ b i } .
Везде далее мы будем предполагать, что задача (1) является невырожденной, то есть
V i = j : H i = H j ( i,j G { 1,.. .,m } ).
Определение 2. Полупространство H i+ , порождаемое гиперплоскостью H i , является рецессивным относительно вектора c , если
|
V x G H i , V A G R >o : x - Ac G H + Л x - Ac / H i . (10) |
Другими словами, луч, исходящий из гиперплоскости H i в направлении противоположном вектору c , полностью лежит в H i+ , но не в H i .
Утверждение 1. Необходимым и достаточным условием рецессивности полупространства H i + относительно вектора c является условие
|
( Q i ,c ) > 0. (11) |
Доказательство. Докажем сначала необходимость. Пусть выполняется условие (10) . Из (7) следует
|
x | a i||2 G H i " (12) |
|
|
Из (5) следует |
A = | a , | 2 G ® >0 ' (13) |
Сопоставляя (10) , (12) и (13) получаем
|
-b i a i H+; l « i | 2 l « i | 2 c G i ; biai 1 H l « i | 2 l ^ i | 2 c G H i . |
С учетом (7), (8) отсюда следует, что a a, Й2 1^1112 c) < b- (14)
Выполнив несложные преобразования неравенства (14) , получаем (11) .
Доказательство достаточности проведем от противного. Предположим, что имеет место (11) и существуют x G Hi и A > 0 такие, что x - \lambdac in/ Hi vee x - \lambdac in Hi .
В соответствии с (7) , (8) это означает
(ai,x - Ac) > bi, что равносильно
( a i ,x} - A ( a i ,c ) > b i .
Так как A > 0 , то в силу (11) отсюда получаем
(ai,x) > bi, что противоречит предположению x \in Hi .
Определение 3. Зафиксируем точку z \in \BbbR n такую, что полупространство
H + = { x E R n |( c,x - z ) < 0 } (15)
включает в себя многогранник M :
M C H c + .
Полупространство H + в этом случае будем называть целевым полупространством, а гиперплоскость H c , определяемую уравнением
Hc = {x E Rn|(c,x - z) =0} , будем называть целевой гиперплоскостью.
Обозначим через ^ c (x) ортогональную проекцию точки x на целевую гиперплоскость H c :
\langle c,x - z \rangle
^c(x) = x--—c.(17)
H c h 2
Здесь || • || обозначает евклидову норму. Определим расстояние p c ( x' ) от точки x E H + до целевой гиперплоскости H c следующим образом:
Pc(x) = |K(x) - x|.
Сопоставляя (15) , (17) и (18) находим, что в этом случае расстояние p c (x) может быть вычислено следующим образом:
Pc(x)= '
Справедливо следующее утверждение.
Утверждение 2. Для любых x,y Е H c +
P c ( x ) ^ P c (y) ^ ( c,x ) > ( c,y ) .
Визуальное представление многомерных задач линейного программирования Доказательство. Используя (19) , получаем
\langle c, z - x \rangle \langle c, z - y \rangle
^c(x) < Pcto) « к1СГ2 < .
\leftrightarrow langle c,z - x rangle \leqslant langle c,z - y rangle
О ( c, z ) + ( c, - x < ( c, z ) + ( c, - y )
\leftrightarrow langle c, - x rangle \leqslant langle c, - y rangle
\leftrightarrow langle c, x rangle \geqslant langle c, y rangle .
В соответствии с утверждением 2 задача (1) эквивалентна следующей задаче:
x = arg min { p c (x) | x G M } .
Определение 4. Пусть полупрос ра c. Целевой проекцией ^i(x) точки x E Rn на рецессивное полупространство H^ называется точка, определяемая формул
^Х^) = X - (Тг^С,
где ai(x) = min {с Е R^o | х — ас Е Н^} .
Примеры целевых проекций в R 2 приведены на рис. 1.
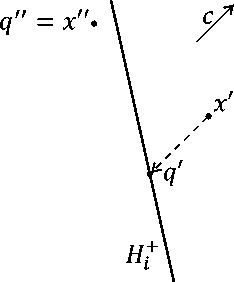
Рис. 1. Целевые проекции в пространстве R 2 : ^ i ( x ' ) = q'; ^ i (x") = q " = x '
Следующее утверждение предоставляет формулу для вычисления целевой проекции на полупространство, рецессивное относительно вектора c .
Утверждение 3. Пусть полупространство H i+ , определяемое неравенством
(ai,x) < bi,(22)
является рецессивным относительно вектора c. Пусть g /н+.(23)
Тогда
( a i , g) - b i
7i(g) = gtt—\—c.
langle a i , c rangle
Доказательство. В соответствии с определением 4 имеем
7 i (g) = g - ^ i (g)c,
где
CT i ( x ) = min {ст G R ^ g I x — ctc G H i+ } .
Таким образом, нам необходимо показать, что
( a i ,g ) — b i ^ a i , c )
= min {ст G R ^ g | x - ctc G H + } .
Рассмотрим прямую L , задаваемую параметрическим уравнением
L = { g + tc | t G R } .
Пусть точка q является пересечением прямой L с гиперплоскостью H i :
q = L П H i .
Тогда q должна удовлетворять уравнению
q = g + T ' c
при некотором \tau \prime \in \BbbR . Подставим правую часть уравнения (27) в уравнение (6) вместо x :
a Q i ,g + t ' c) = b i .
Отсюда
{ a i ,g) + t ' { a i , c ) = b i ,
' = b i - ( Q i ,g )
T { a i ,c) ‘
Подставив вместо \tau \prime правую часть уравнения (28) в формулу (27) получаем
. bi — ( a i ,g ) q = g + ——^c, langle a i , c rangle
что эквивалентно
( a i ,g} - b i q = g-- p—c—c.
langle a i , c rangle
Так как q \in H i в соответствии с (26) , формула (25) будет иметь место, если мы покажем, что
CTa G R > g : ст < a i’ g^ - ^i ^ g — ctc G H + .
langle a i , c rangle i
Предположим противное, то есть существует ст ' > 0 такое, что
\sigma prime
< ( a i ,g ) — b i
< a i ,c )
и g — ct'c G H+
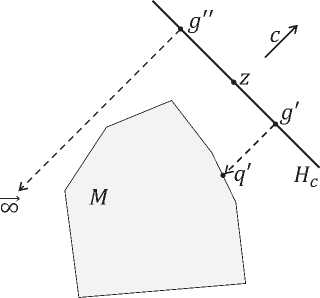
Рис. 2. Целевые проекции на многогранник M в пространстве R 2 : 7 м (g ' ) = q;
7 м ( g " ) = »
Тогда из (22) и (32) следует
(ai,g - ст'е) ^ bi, что равносильно
( a i ,g )- b i ^ ст ' ( a i ,c ) . (33)
В силу утверждения 1 имеем (di,c) > 0. Поэтому (33) равносильно kai i g) — bi / ' \leqslant\sigma.
\langle a i , c \rangle
Получили противоречие с (31) .
Определение 5. Пусть g Е H c . Целевой проекцией 7 м (g) точки g на многогранник M называется точка, определяемая формулой
7 м ( g ) = g - ст м ( g ) c , (34)
где ст м ( g) = min { ст Е М ^ о | g — ctc Е M } .
Если
^3 ст Е R70 : g — ctc Е M, полагаем 7м(g) = 00 — точка, бесконечно удаленная от M.
Примеры целевых проекций на многогранник M в \BbbR 2 приведены на рис. 2.
Определение 6. Рецептивным полем © ( z,g,6 ) С H c плотности 6 Е R >o с центром в точке z \in H c и рангом \eta \in \BbbN будем называть конечное упорядоченное множество точек, удовлетворяющих следующим условиям:
z Е ©(z, 7, 6);
Vg Е ©(z,7, 6): ||g — z\\ < gS^n;(36)
gggg" E ©(z,g,6) : g' = g'' ^ \g' — g''\ > 6;
Vg' Е ©(z, g, 6) 3g'' Е ©(z, g, 6) : |g' — g"\ = 6;(38)
Vx Е Co(©(z, g, 6)) 3g Е ©(z, 7, 6) : \\g — x| < 16^n.(39)
Здесь Co(X) обозначает выпуклую оболочку конечного множества точек
X = { x (1) ,...,x ( K ) } С R n :
Co ( X ) =
K
£ A i x ( i )
A i E R ^ g
. £ A i = 1}- i=1 )
Точки рецептивного поля будем называть рецептивными точками .
Формула (35) в определении 6 означает, что точка, находящаяся в центре рецептивного поля, принадлежит этому полю. Из формулы (36) следует, что любая точка g рецептивного поля отстоит от центральной точки z на расстояние не более \eta\delta n . В соответствии с формулой (37) для любых двух различных точек g ' = g " рецептивного поля расстояние между ними не может быть меньше \delta . Формула (38) говорит, что для любой точки g \prime рецептивного поля найдется точка g \prime\prime , принадлежащая этому же полю, такая, что расстояние между g \prime и g \prime\prime будет равно \delta . Формула (39) означает, что для любой точки x , принадлежащей выпуклой оболочке рецептивного поля, в этом поле найдется точка g , отстоящая от x на расстояние не более | 5 ^ п. Пример рецептивного поля в пространстве R 3 приведен на рис. 3.
Опишем конструктивный метод построения рецептивного поля. Без ограничения общности мы можем предполагать, что c n = 0 . Построим в R n следующий ортогональный базис, включающий в себя вектор c :
c (G) = c = (c i , С 2 , C 3 , C 4 , .. - , C n-1 , C n );
-
(1) = j (—£ £ i=2 c 2 , c 2 , c 3 , c 4 , . . . , c n-1 , c n) , если c i = 0;
I (1, 0,..., 0), если c 1 = 0;
-
(2) = J (° — c 2 £ i=3 c 2 , c 3 , C 4 ■•••■ c n - 1 , c") , если c 2 = 0
I (0,1, 0,..., 0), если c 2 = 0;
-
(3) = J (0 0, — c 33 £ i=4 c 2 , c 4 , - - - , c n-1 , c n) , если C 3 = 0;
I (0, 0,1, 0,..., 0), если c 3 = 0;
c (n-2)
c (n-1)
( 0,..., 0, - c 2 ,C n - 1 ,cTa , если C n-2 = 0; \ c n - 2 Z ^i = n- 1 /
(0,..., 0,1, 0, 0), если c n - 2 = 0;
0 0,..., 0, - c n - i, cn) , если c n-1 = 0;
(0,..., 0, 0,1, 0), если c n - 1 = 0.
Непосредственно проверяется, что
V i, j € { 0,1,... ,n - 1 } ,i = j : ^ c ( i ) ,c ( j ) ) = 0.
В частности
V i = 1, . . . , n - 1 : c, c ( i ) = 0.
. ®с (z, ц, 5) ,
*-------; ;-------*-------; L ^5
Рис. 3. Рецептивное поле в пространстве R 3
Следующее утверждение показывает, что линейное подпространство размерности (n — 1) , порождаемое ортогональными векторами c i ,..., c n - 1 , является гиперплоскостью, параллельной гиперплоскости H c .
Утверждение 4. Определим линейное подпространство S c С R n размерности n — 1 :
Тогда
S c
{ n—1
Е A i
\lambda i \in \BbbR .
V s G S c : s + z G H c .
Доказательство. Пусть s \in Sc , то есть s = A^1) + ... + An-1c(n 1).
д ( c, (s + z ) — z ) = A i ( c, c (1) } + ... + A n-1 ( c, c (n - 1) } .
Отсюда в силу (40) получаем
( c, ( s + z ) — z ) = 0.
Сопоставляя это с (16) , имеем s + z G H c . □
Определим векторы
c (i)
e ( i ) = (i = 1,...,n — 1), (43)
Hc(i)H образующие ортонормированный базис подпространства Sc .
Процедура построения рецептивного поля представлена в виде алгоритма 1. Этот ал горитм строит рецептивное поле ©(z/q,6), состоящее из
K 6 = (2^ + 1) n - 1
точек, расположенных в узлах регулярной решетки, имеющей форму гиперквадрата (гиперкуба размерности n — 1 ) с длиной ребра, равной 2^5 . Длина ребра ячейки гиперквадрата равна \delta . В соответствии с шагом 13 алгоритма 1 и утверждением 4 этот гиперквадрат лежит в гиперплоскости H c и имеет центр в точке z . Недостаток алгоритма 1 состоит в том, что количество вложенных циклов for зависит от размерности пространства. Эту проблему можно решить с помощью функции G , вычисляющей точку рецептивного множества по ее 40 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»
Алгоритм 1 Построение рецептивного поля ®(z,^, 5)
Require: z G H c , ^ G N , 5 G R > q
-
1: 0 : = 0
-
2: for i n-1 = 0 ... 2^ do
-
3: s n-1 : = i n - 1 5 — ^5
-
4: for i n - 2 = 0 ... 2^ do
-
5: S n-2 : = i n-2 5 - ^5
-
6: . . .
-
7: for i 1 = 0 ... 2^ do
-
8: s 1 : = i 1 5 — ^5
-
9: s : = 0
-
10: for j = 1... n — 1 do
-
11: s : = s + S j e ( j )
-
12: end for
-
13: 0 : = 0 U { s + z }
-
14: end for
-
15: end for
-
16: end for
Алгоритм 2 Функция G вычисляет точку рецептивного поля по ее номеру к
Require: z G H c , ^ G N , 5 G R > q
-
1: function G ( k, n, z, \eta, \delta )
-
2: for j = (n — 1) . . . 1 do
-
3: l j : = [ k/(2^ + 1) j - 1 J
-
4: к : = к mod (2^ + 1) j - 1
-
5: end for
-
6: g : = z
-
7: for j = 1 . . . (n — 1) do
-
8: g : = g + ( l j 5 — ^5)e ( j )
-
9: end for
-
10: G : = g
-
11: end function
порядковому номеру (нумерация начинается с нуля; порядок определяется алгоритмом 1) . Реализация функции G представлена в виде алгоритма 2. Следующее утверждение 5 дает оценку временной сложности алгоритма 2.
Утверждение 5. Алгоритм 2 допускает реализацию с временной сложность ю1
C G = 4n 2 + 5n — 9,
где n — размерность пространства.
Доказательство. Рассмотрим низкоуровневую реализацию алгоритма 2, представленную в виде алгоритма 3.
Алгоритм 3 Низкоуровневая реализация алгоритма 2
-
1: p : = 2p + 1 ; r : = p5; h : = p n - 2 ; g : = z
-
2: j : = n — 1
-
3: repeat
-
4: l j : = L k/h J
-
5: k : = k mod h
-
6: h : = h/p
-
7: j : = j - 1
-
8: until j = 0
-
9: j : = 1
-
10: repeat
|
11: |
W j : = l j 5 — r |
|
12: |
i : = 1 |
|
13: |
repeat |
|
14: |
g i : = g i + w j e j |
|
15: |
i : = i + 1 |
|
16: |
until i > n |
|
17: |
j : = j + 1 |
18: until j = n
Значения, вычисляемые на шагах 1–2 алгоритма 3, не зависят от номера рецептивной точки k и поэтому могут считаться константами. Цикл repeat/until на шагах 3–8 выполняется (n — 1) раз и требует с з:8 = 5(n — 1) операций. Вложенный цикл repeat/until на шагах 13-16 выполняется n раз и требует C i3:ia = 4n операций. Внешний цикл repeat/until на шагах 10-18 выполняется (n — 1) раз и требует c io:i8 = (4 + c i3-ie )(n — 1) = 4(n 2 — 1) операций. В сумме получаем
C G = C 3:8 + C i0:i8 = 4 n 2 + 5n — 9.
Следствие 1. Временная сложность алгоритма 2 может быть оценена как O(n 2 ) .
Определение 7. Пусть z Е H c . Зафиксируем p Е N , 5 G R >o . Образом 3 ( z, p, 5) , порожденным рецептивным полем 6(z, p, 5) , будем называть упорядоченное множество вещественных чисел
3(z,^,5) = { р с ( ^ м (g)) | g Е ©(z,^,5) } . (46)
Порядок чисел в образе определяется порядком соответствующих точек рецептивного поля.
Функцию построения образа 3 ( z, p, 5) в виде списка чисел представлена в виде алгоритма 4. Здесь [] обозначает пустой список, а -+ обозначает операцию конкатенации списков.
Алгоритм 4 Построение образа 3 ( z,p,6 )
Require: z Е Hc, p E N , 6 E R >o
-
1: function 3 ( z,p, 6 )
-
2: 3 : = []
-
3: for k = 0 ... ((2p + 1) n - 1 — 1) do
-
4: g k : = G(k, n, z, p, 6)
-
5: 3 : = 3 — [ p c ( ^ M ( g k ))]
-
6: end for
-
7: end function
Покажем как полученный образ может быть использован для решения задачи ЛП. Пусть (ai,c) > 0. Это означает, что полупространство Hi+ является рецессивным относительно вектора c (см. утверждение 1). Пусть имеется точка u \in Hi \cap M. Допустим, что нам удалось создать искусственную нейронную сеть DNN, получающую на входе образ 3(vc(u),p,6) окрестности точки и, и выдающую на выходе точку и' такую, что и' = arg min {pc(x) |x E Hi П M} .
Тогда мы можем построить алгоритм 5, решающий задачу линейного программирования (20) с помощью DNN.
Алгоритм 5 Линейное программирование с использованием DNN
Require: u (1) E H i П M, ( a i , c ) > 0, z E H c ; p E N, 6 E R >o
-
1: k : =1
-
2: repeat
-
3: I : = 3 ( u (k) ,p,6 )
-
4: u ( k +1) : =DNN( I )
-
5: k : = k - 1
-
6: until U ( k ) = U ( k - 1)
-
7: x : = u ( k )
-
8: stop
-
2. Параллельный алгоритм построения образа задачи ЛП
При решении задач ЛП большой размерности и с большим количеством ограничений алгоритм 4 построения образа задачи ЛП может потребовать значительных временных затрат. В этом разделе приводится его параллельная версия, позволяющая существенно сократить время решения задачи ЛП с помощью алгоритма 5. Параллельная версия алгоритма 4 строится на основе модели параллельных вычислений BSF [24, 25] , ориентированной на кластерные вычислительные системы. Модель BSF использует парадигму мастер–рабочие и требует представление алгоритма в форме операций над списками с использованием функций высшего порядка Map и Reduce , определенных в формализме Бёрда—Миртенса (Bird–Meertens formalism) [26] . Модель BSF также предоставляет метрику для аналитиче-
Визуальное представление многомерных задач линейного программирования ской оценки масштабируемости параллельного алгоритма, удовлетворяющего указанным требованиям.
Представим алгоритм 4 в форме операций над списками с использованием функций высшего порядка Map и Reduce . В качестве списка, обрабатываемого функцией высшего порядка Map , возьмем список номеров неравенств системы (4) :
\scrL
map
[1,..., m] .
Обозначим R ^ = R U {то} . Определим следующим образом параметризованную функцию
F k : { 1,..., m } ^ R ^ , являющуюся первым параметром функции высшего порядка Map :
F k (i) =
I
P c ( l i ( g k )), если ( a i , c ) > 0 и ^ i ( g k ) E M ; то , если ( a i , c ) < 0 или ^ i ( g k ) / M,
где g k = G ( k, n, z, P, 5 ) вычисляется с помощью алгоритма 2, а p i ( g k ) вычисляется по формуле (24) . С неформальной точки зрения функция F k отображает номер полупространства H + в расстояние от целевой проекции до целевой гиперплоскости, если H i+ является рецессивным относительно c (см. утверждение 1) и целевая проекция принадлежит M . В противном случае F k возвращает специальное значение \то .
Функция высшего порядка Map преобразует список scrL map в список scrL reduce путем применения функции F k к каждому элементу списка £ map :
scrL reduce = Map(F k , scrL map ) = [F k (1),...,F k (m)] = [p i ,.. .,P m ] .
Определим бинарную ассоциативную операцию (J : R ^ ^ R ^ следующим образом:
\infty \bigcircdownarrow \infty то;
a;
min(a, p).
V a E R : a (J) то
V a,p E R : a (J p
С неформальной точки зрения операция bigcircdownarrow вычисляет минимальное из двух чисел.
Функция высшего порядка Reduce преобразует список scrL reduce в атомарное значение \rho in \BbbR \infty путем последовательного применения операции bigcircdownarrow ко всему списку:
Reduce(( D , £^uce ) = P i (D P 2 (D ... (J P m = p.
Построение образа \frakI задачи ЛП с использованием функций высшего порядка Map и Reduce представлено в виде алгоритма 6. Параллельная версия алгоритма 6 строится на основе алгоритмического шаблона 2 из [24] . Результат представлен в виде алгоритма 7. Прокомментируем параллельный алгоритм 7. Для простоты мы будем предполагать, что количество ограничений m кратно количеству рабочих L и нумерация неравенств начинается с нуля. Параллельный алгоритм включает в себя L + 1 процесс: один процесс-мастер (кратко — мастер) и L процессов-рабочих (кратко — рабочие). Мастер управляет вычислениями. Первоначально в качестве образа \frakI берется пустой список (шаг 2 мастера). Текущий номер k полагается равным нулю (шаг 3 мастера). На шагах 4–15 мастер организует цикл repeat/until , в котором строится образ \frakI задачи ЛП. На шаге 5 мастер посылает номер очередной рецептивной точки k всем рабочим. На шаге 8 мастер ожидает получение
Алгоритм 6 Построение образа \frakI с использованием Map и Reduce
Require: z E H c , ^ E N , 6 E R > q
-
1: input n, m, A, b, c, z, \eta, \delta
-
2: 3 : = []
-
3: ^ map • = [1> • • • , m]
-
4: for k = 0 • • • ((2 p + 1) n - 1 — 1) do
6:
7:
^ reduce • Map(F k , C m^ p • Reduce ((X) , ^ reduce ) 3 : = 3 -H- [p]
-
8: end for
-
9: output \frakI
-
10: stop
Алгоритм 7 Параллельный алгоритм построение образа \frakI задачи ЛП
Каждый l -тый рабочий выполняет общую последовательность действий, но над своей частью £ map ( t ) списка £ map , которая определяется на шаге 3. На шаге 4 рабочий входит в цикл repeat/until . На шаге 5 он получает номер очередной точки k , принадлежащей рецептивному полю. На шаге 6 рабочий обрабатывает свой подсписок £ map ( t ) , используя функцию высшего порядка Map , которая для каждого элемента подсписка выполняет параметризованную функцию F k , определенную с помощью формулы (48) . В результате получается подсписок C reducep ) , содержащий расстояния F k (i) от целевой гиперплоскости H c до целевых проекций рецептивной точки g k на гиперплоскости H i для всех i из подсписка £ map(i) . На шаге 7 рабочий с помощью функции высшего порядка Reduce редуцирует подсписок £ reduce ( i ) в атомарное значение p i , используя ассоциативную бинарную операцию \bigcirc\downarrow , вычисляющую минимальное расстояние. Полученный частный результат пересылается мастеру (шаг 8 рабочего). На шаге 13 рабочий ожидает получение от мастера значения булевой переменной exit . Если получено значение false, рабочий продолжает выполнение цикла repeat/until (шаг 14 рабочего). В противном случае процесс рабочего завершается на шаге 16.
Дадим аналитическую оценку границы масштабируемости параллельного алгоритма 7 с использованием стоимостной метрики модели параллельных вычислений BSF [24] . Под границей масштабируемости здесь понимается число рабочих, на котором достигается максимум ускорения. Стоимостная метрика модели BSF включает в себя следующие стоимостные параметры для цикла repeat/until (шаги 4–14) параллельного алгоритма 7:
m : длина списка \scrL map ;
D : латентность (время пересылки одно байта от мастера к рабочему);
t c : время, затрачиваемое мастером на пересылку одному рабочему координат рецептивной точки и получения от него расстояния от этой точки до целевой проекции (включая латентность);
t Map : время, затрачиваемое одним рабочим на выполнение функции высшего порядка Map для всего списка \scrL map ;
t a : время, затрачиваемое на выполнение одной бинарной операции \bigcirc\downarrow .
В соответствии с формулой (14) из [24] граница масштабируемости параллельного алгоритма 7 может быть оценена следующим образом:
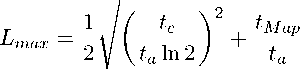
+ 4m —
tc ta In 2 ‘
Вычислим оценку для временных параметров формулы (49) . Для этого ведем следующие обозначения в рамках одной итерации цикла repeat/until (шаги 4–14) параллельного алгоритма 7:
cc : количество числе, пересылаемых от мастера к рабочему и обратно в рамках одной итерации;
c Map : количество арифметических операций и операций сравнения, выполняемых на шаге 5 последовательного алгоритма 6;
c a : количество операций, необходимых для выполнения бинарной операции \bigcirc\downarrow .
В начале каждой итерации мастер посылает каждому рабочему номер рецептивной точки. В ответ рабочий посылает расстояние от этой точки до целевой проекции. Следовательно cc = 2. (50)
В контексте алгоритма 6
C Map = (C G + C F k ) m, (51)
где c G — количество операций, необходимых для вычисления координат точки g k , c F k — количество операций, необходимых для вычисления функции F k (i) по формуле (48) в предположении, что координаты точки g k уже вычислены. Оценка значения c G дана в предложении 5. Оценим значение C F k . В соответствии с (24) вычисление целевой проекции ^ i ( g k ) требует (6n — 2) арифметических операций. Из (19) следует, что вычисление р с ( х) составляет (5n — 1) арифметических операций. Проверка условия x G M в соответствии с (4) потребует m (2 n — 1) арифметических операций и m операций сравнения. Таким образом
CFk = 2mn + 11n — 3.
Подставив в (51) правые части формул (45) и (52) , получаем
CMap = 4n2m + 2m2 n + 16nm — 12m.
Для выполнения бинарной операции \bigcirc\downarrow необходимо выполнить одну операцию сравнения:
Ca = 1.
Пусть \tauop — среднее время выполнения арифметических операций и операций сравнения, \tautr — среднее время для пересылки одного вещественного числа без учета латентности. Тогда, используя формулы (50), (53) и (54), получаем tc = CcTtr + 2D = 2(Ttr + D);
t Map = C Map T op = (4n 2 m + 2 m 2 n + 16nm — 12m)T op ;
t a = C a T op = T op .
Подставив в (49) правые части формул (55) – (57) , получим следующую оценку границы масштабируемости параллельного алгоритма 7:
_ 1 I / 2(Ttr + D) L max = „ 1 / _ , „
2 V V T op in 2
+ 4n 2 m + 2 m 2 n + 16nm — 12m —
2(T tr + D) T op In 2
.
Для больших значений m и n это эквивалентно
L max ~ O( V2n 2 m + m 2 n + 8nm — 6m). (58)
Если предположить, что m = O(n) , то из (58) следует
L max ~ O ( nVn ) , (59)
Таблица 1. Характеристики кластера «Торнадо ЮУрГУ»
-
3. Вычислительные эксперименты
Нами была выполнена параллельная реализация алгоритма 7 в виде программы ViLiPP (Visualization of Linear Programming Problem) на языке C++ с использованием программного BSF-каркаса [27, 28]. BSF-каркас базируется на модели параллельных вычислений BSF и инкапсулирует все аспекты, связанные с распараллеливанием программы с использованием библиотеки MPI [29] и программного интерфейса OpenMP [30]. Исходные коды программы ViLiPP свободно доступны в сети Интернет по адресу nikolay-olkhovskiy/LP-visualization-MPI. С использованием параллельной программы ViLiPP мы провели эксперименты по исследованию масштабируемости алгоритма 7 на кластерной вычислительной системе «Торнадо ЮУрГУ» [31], характеристики которой приведены в таблице 1.
С помощью генератора задач «FRaGenLP» [32, 33] для проведения вычислительных экспериментов были сгенерированы три случайные задачи ЛП, параметры которых приведены в таблице 2. Количество ненулевых значений матрицы A задачи (1) всех случаях составило 100%. Для всех задач ранг рецептивного поля \eta полагался равным 2 . В соответствии с формулой (44) мощность рецептивного поля демонстрировала экспоненциальный рост с увеличением размерности пространства.
Результаты вычислительных экспериментов приведены в таблице 3 и на рис. 4. Во всех запусках каждому рабочему выделялся отдельный процессорный узел. Еще один дополнительный процессорный узел выделялся для работы мастера. Вычислительные эксперименты показали, что с ростом размерности задачи наблюдается рост границы масштабируемости программы ViLiPP: для LP5 максимум кривой ускорения достигается в районе 190 узлов, для LP6 максимум располагается в районе 260 узлов, а для LP7 он приблизительно равен 326 узлам. При этом наблюдается экспоненциальный рост времени решения задачи: образ задачи LP5 на 11 процессорных узлах строится за 10 сек., а построение образа задачи LP7 на таком же количестве узлов требует уже 5 мин. Дополнительный вычислительный
Таблица 2. Параметры тестовых задач ЛП
|
Идентификатор задачи |
Число переменных |
Число ограничений |
Процент ненулевых значений в A |
Мощность рецептивного поля |
|
LP7 |
7 |
4016 |
100% |
15 625 |
|
LP6 |
6 |
4014 |
100% |
3125 |
|
LP5 |
5 |
4012 |
100% |
625 |
Таблица 3. Время построения образа задач ЛП (сек.)
|
Число процессорных узлов |
LP5 |
LP6 |
LP7 |
|
11 |
9.81 |
54.45 |
303.78 |
|
56 |
1.93 |
10.02 |
59.43 |
|
101 |
1.55 |
6.29 |
33.82 |
|
146 |
1.39 |
4.84 |
24.73 |
|
191 |
1.35 |
4.20 |
21.10 |
|
236 |
1.38 |
3.98 |
19.20 |
|
281 |
1.45 |
3.98 |
18.47 |
|
326 |
1.55 |
4.14 |
18.30 |
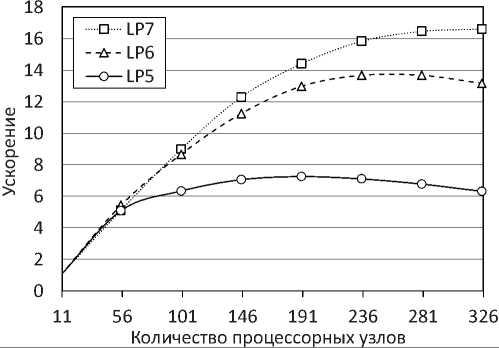
Рис. 4. Графики ускорения параллельной программы ViLiPP для задач ЛП различного размера эксперимент показал, что построение образа задачи при n = 9 на 11 процессорных узлах занимает 1.5 часа.
Проведенные эксперименты позволяют сделать вывод, что при современном уровне развития вычислительной техники применение искусственных нейронных сетей для решения задач ЛП на основе предложенного метода визуализации может быть эффективным для задач размерности, не превышающей 100, с количеством ограничений до 100 000.
Заключение
Основным результатом, полученным в данной работе, является математическая модель визуального представления многомерной задачи линейного программирования по поиску в допустимой области точки максимума линейной целевой функции. Основным элементом модели является рецептивное поле, представляющее собой регулярное множество точек, располагающихся в узлах решетки, построенной внутри гиперкуба. Все точки рецептивного поля лежат в целевой гиперплоскости, ортогональной вектору c = (c i ,..., c n ) , составленному из коэффициентов линейной целевой функции. Целевая гиперплоскость располагается так, что для любой точки x из допустимой области и любой точки z целевой гиперплоскости выполняется неравенство \langle c, x \rangle < \langle c, z \rangle . Можно сказать, что рецептивное поле является многомерным абстрактным аналогом светочувствительной матрицы цифрового фотоаппарата. Из каждой точки рецептивного поля в направлении допустимой области строится луч, параллельный вектору c . Точка, в которой луч касается допустимой области, называется целевой проекцией. Образ задачи линейного программирования представляет собой матрицу положительных вещественных чисел размерности ( п — 1) , в которой каждый элемент является расстоянием от точки рецептивного поля до соответствующей точки целевой проекции.
В статье описан алгоритм вычисления координат точки рецептивного поля по ее порядковому номеру. Показано, что временная сложность этого алгоритма может быть оценена как O(n 2 ) , где п — размерность пространства. Приведено общее описание алгоритма решения задачи линейного программирования с помощью искусственной нейронной сети на основе анализа построенных образов. Предложен параллельный алгоритм построения образа задачи линейного программирования, ориентированный на кластерные вычислительные системы. Этот алгоритм основывается на модели параллельных вычислений BSF, предполагающей использование парадигмы мастер–рабочие и представление алгоритма в виде операций над списками с использованием функций высшего порядка Map и Reduce . Показано, что для границы масштабируемости параллельного алгоритма справедлива оценка О ( пл/п ) . Это означает, что алгоритм демонстрирует хорошую масштабируемость.
Выполнена реализация параллельного алгоритма построения образа задачи линейного программирования на языке C++ с использованием параллельного программного BSF-каркаса, инкапсулирующего все аспекты, связанные с распараллеливанием на основе библиотеки MPI и программного интерфейса OpenMP. С использованием этой программной реализации на вычислительном кластере «Торнадо ЮУрГУ» проведены масштабные вычислительные эксперименты по построению образов для случайных многомерных задач линейного программирования с большим числом ограничений. Проведенные эксперименты подтверждают корректность и эффективность предложенных подходов. Вместе с тем следует отметить, что время построение образа растет экспоненциально с увеличением размерности пространства. Поэтому предложенный метод применим для задач с числом переменных, не превышающим 100. При этом количество ограничений теоретически может быть неограниченным.
В качестве направлений дальнейших исследований можно выделить следующие.
-
1. Разработать метод решения задачи линейного программирования на основании анализа ее образов и доказать его сходимость.
-
2. Разработать и реализовать метод построения обучающих множеств для создания нейронной сети, решающей задачи линейного программирования путем анализа их образов.
-
3. Разработать и обучить искусственную нейронную сеть для решения многомерные задачи линейного программирования.
-
4. Разработать и реализовать на вычислительном кластере параллельную программу, строящую многомерные образы задачи линейного программирования и получающую ее решение с помощью искусственной нейронной сети.
Исследование выполнено при финансовой поддержке РФФИ (грант 20-07-00092 а) и Министерства науки и высшего образования РФ (государственное задание FENU-2020-0022).
Список литературы Визуальное представление многомерных задач линейного программирования
- Jagadish H.V., Gehrke J., Labrinidis A., et al. Big data and its technical challenges // Communications of the ACM. 2014. Vol. 57, no. 7. P. 86-94. DOI: 10.1145/2611567.
- Hartung T. Making Big Sense From Big Data // Frontiers in Big Data. 2018. Vol. 1. P. 5. DOI: 10.3389/f data. 2018.00005.
- Соколинская И., Соколинский Л. О решении задачи линейного программирования в эпоху больших данных // Параллельные вычислительные технологии (ПаВТ’2017). Короткие статьи и описания плакатов. Челябинск: Издательский центр ЮУрГУ, 2017. С. 471—484. URL: http://omega.sp.susu.ru/pavt2017/short/014.pdf.
- Chung W. Applying large-scale linear programming in business analytics // 2015 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM). IEEE, 2015. P. 1860-1864. DOI: 10.1109/IEEM.2015.7385970.
- Gondzio J., Gruca J.A., Hall J.A.J., et al. Solving large-scale optimization problems related to Bell’s Theorem // Journal of Computational and Applied Mathematics. 2014. Vol. 263. P. 392-404. DOI: 10.1016/j . cam. 2013.12.003.
- Sodhi M.S. LP modeling for asset-liability management: A survey of choices and simplifications // Operations Research. 2005. Vol. 53, no. 2. P. 181-196. DOI: 10.1287/opre. 1040. 0185.
- Brogaard J., Hendershott T., Riordan R. High-Frequency Trading and Price Discovery // Review of Financial Studies. 2014. Vol. 27, no. 8. P. 2267-2306. DOI: 10.1093/rf s/hhu032.
- Дышаев M.M., Соколинская И.М. Представление торговых сигналов на основе адаптивной скользящей средней Кауфмана в виде системы линейных неравенств // Вестник Южно-Уральского государственного университета. Серия: Вычислительная математика и информатика. 2014. Т. 2, № 4. С. 103—108. DOI: 10.14529/cmsel30408.
- Bixby R.E. Solving Real-World Linear Programs: A Decade and More of Progress // Operations Research. 2002. Vol. 50, no. 1. P. 3-15. DOI: 10.1287/opre. 50.1.3.17780.
- Dongarra J., Gottlieb S., Kramer W.T.C. Race to Exascale // Computing in Science and Engineering. 2019. Vol. 21, no. 1. P. 4-5. DOI: 10.1109/MCSE. 2018.2882574.
- Dantzig G.B. Linear programming and extensions. Princeton, N.J.: Princeton university press, 1998. 656 p.
- Zadeh N. A bad network problem for the simplex method and other minimum cost flow algorithms // Mathematical Programming. 1973. Vol. 5, no. 1. P. 255-266. DOI: 10.1007/ BF01580132.
- Tolla Р. A Survey of Some Linear Programming Methods // Concepts of Combinatorial Optimization / ed. by V.T. Paschos. 2nd ed. Hoboken, NJ, USA: John Wiley, Sons, 2014. Chap. 7. P. 157-188. DOI: 10.1002/9781119005216. ch7.
- Mamalis B., Pantziou G. Advances in the Parallelization of the Simplex Method // Algorithms, Probability, Networks, and Games. Lecture Notes in Computer Science, vol. 9295 / ed. by C. Zaroliagis, G. Pantziou, S. Kontogiannis. Cham: Springer, 2015. P. 281-307. DOI: 10.1007/978-3-319-24024-4_17.
- Karmarkar N. A new polynomial-time algorithm for linear programming // Combinatorica. 1984. Vol. 4, no. 4. P. 373-395. DOI: 10.1007/BF02579150.
- Yuan Y. Implementation tricks of interior-point methods for large-scale linear programs // Proc. SPIE, vol. 8285. International Conference on Graphic and Image Processing (ICGIP 2011). International Society for Optics, Photonics, 2011. DOI: 10.1117/12.913019.
- Ершова А.В., Соколинская И.М. О сходимости масштабируемого алгоритма построения псевдопроекции на выпуклое замкнутое множество / / Вестник Южно-Уральского государственного университета. Серия: Математическое моделирование и программирование. 2011. № 37(254). С. 12—21. URL: https://mmp.susu.ru/article/ru/127.
- Hafsteinsson Н., Levkovitz R., Mitra G. Solving large scale linear programming problems using an interior point method on a massively parallel SIMD computer // Parallel Algorithms and Applications. 1994. Vol. 4, no. 3-4. P. 301-316. DOI: 10.1080/10637199408915470.
- Karypis G., Gupta A., Kumar V. A parallel formulation of interior point algorithms // Proceedings of the 1994 ACM/IEEE conference on Supercomputing (Supercomputing’94). Los Alamitos, CA, USA: IEEE Computer Society Press, 1994. P. 204-213. DOI: 10.1109/ SUPERC.1994.344280.
- Prieto A., Prieto B., Ortigosa E.M., et al. Neural networks: An overview of early research, current frameworks and new challenges // Neurocomputing. 2016. Vol. 214. P. 242-268. DOI: 10.1016/j .neucom.2016.06.014.
- Schmidhuber J. Deep learning in neural networks: An overview // Neural Networks. 2015. Vol. 61. P. 85-117. DOI: 10.1016/j .neunet.2014.09.003.
- LeCun Y., Bengio Y., Hinton G. Deep learning // Nature. 2015. Vol. 521, no. 7553. P. 436-444. DOI: 10.1038/nature 14539.
- Lachhwani K. Application of Neural Network Models for Mathematical Programming Problems: A State of Art Review // Archives of Computational Methods in Engineering. 2020. Vol. 27. P. 171-182. DOI: 10.1007/sll831-018-09309-5.
- Sokolinsky L.B. BSF: A parallel computation model for scalability estimation of iterative numerical algorithms on cluster computing systems // Journal of Parallel and Distributed Computing. 2021. Vol. 149. P. 193-206. DOI: 10.1016/j . jpdc. 2020.12.009.
- Ежова H.A., Соколинский Л.Б. Модель параллельных вычислений BSF-MR // Системы управления и информационные технологии. 2019. № 3(77). С. 15—21.
- Bird R.S. Lectures on Constructive Functional Programming // Constructive Methods in Computing Science. NATO ASI Series F: Computer and Systems Sciences, vol. 55 / ed. by M. Broy. Berlin, Heidelberg: Springer, 1988. P. 151-216.
- Sokolinsky L.B. BSF-skeleton: A Template for Parallelization of Iterative Numerical Algorithms on Cluster Computing Systems // MethodsX. 2021. Vol. 8. Article 101437. DOI: 10.1016/j.mex.2021.101437.
- Sokolinsky L.B. BSF-skeleton. 2019. URL: https://github.com/leonid-sokolinsky/ BSF-skeleton (дата обращения: 24.01.2022).
- Gropp W. MPI 3 and Beyond: Why MPI Is Successful and What Challenges It Faces // Recent Advances in the Message Passing Interface. EuroMPI 2012. Lecture Notes in Computer Science, vol. 7490 / ed. by J. Traff, S. Benkner, J. Dongarra. Berlin, Heidelberg: Springer, 2012. P. 1-9. DOI: 10.1007/978-3-642-33518-1_1.
- Kale V. Shared-memory Parallel Programming with OpenMP // Parallel Computing Architectures and APIs. Boca Raton: Chapman, Hall/CRC, 2019. Chap. 14. P. 213-222. DOI: 10.1201/9781351029223- 18/SHARED-MEMORY-PARALLEL-PROGRAMMING-OPENMP-VIVEK-KALE.
- Kostenetskiy P., Semenikhina P. SUSU Supercomputer Resources for Industry and fundamental Science // Proceedings - 2018 Global Smart Industry Conference, GloSIC 2018. IEEE, 2018. Article 8570068. P. 1-7. DOI: 10.1109/GloSIC.2018.8570068.
- Соколинский Л.Б., Соколинская И.М. О генерации случайных задач линейного программирования на кластерных вычислительных системах / / Вестник Южно-Уральского государственного университета. Серия: Вычислительная математика и информатика. 2021. Т. 10, № 1. С. 38—52. DOI: 10.14529/cmse210103.
- Соколинский Л.Б. Свидетельство о государственной регистрации программы для ЭВМ № 2021619526 Российская Федерация. Генератор случайных задач линейного программирования FRaGenLP : № 2021618165 : заявл. 28.05.2021 : опубл. 10.06.2021.


