Вязкость жидкого железа: молекулярно-динамический расчет с потенциалом погруженного атома

Железо – доминирующий компонент большинства используемых человечеством металлических конструкций. Механические свойства железа и его сплавов определяются предысторией расплава перед кристаллизацией и условиями кристаллизации [1]. Были обнаружены гистерезис свойств (вязкость, поверхностное натяжение, магнитная восприимчивость, плотность) при нагреве и охлаждении расплава, осцилляция этих свойств со временем. В настоящее время отсутствует общепринятое достоверное описание связи свойств расплава и его внутренней структуры. Экспериментальное исследование структуры и свойств расплавов на основе железа затруднено как в силу ряда технических причин, так и из-за чувствительности расплавов к концентрации компонентов. Молекулярно-динамическое (МД) моделирование [2] с использованием потенциалов погруженного атома [3] позволяет строить модели, соответствующие реальным системам, в частности, в работе [4] был разработан ЕАМ ( Embedded atom method , метод погруженного атома) потенциал для жидкого железа, хорошо предсказывающий температуру плавления, плотность, энергию. В работах [5, 6] предложены различные версии потенциала для железа при больших давлениях и температурах и применены соответственно в [7] и [6] для расчета вязкости в условиях, близких к условиям в ядре Земли.

Данные о температурной зависимости вязкости железа вблизи температуры плавления отсутствуют в настоящее время. Представляется интересным восполнение этого пробела и соотнесение молекулярно-динамических расчетов с экспериментальными данными. Наличие или отсутствие особенностей на функции вязкости может свидетельствовать за или против выбранного взаимодействия, представленного ЕАМ потенциалом. Кроме того, анализ и интерпретация результатов могут приблизить нас к пониманию внутренней структуры расплава железа.

В работе представлен расчет сдвиговой вязкости чистого железа с ЕАМ потенциалом [4]. Расчет проводился в рамках метода равновесной молекулярной динамики с использованием метода Грина–Кубо [8, 9].

Методика расчета

Кинетические коэффициенты, в частности коэффициент сдвиговой вязкости, могут быть определены в рамках теории линейного отклика методом Грина–Кубо [8, 9]. Коэффициент переноса выражается как интеграл от автокорреляционной функции соответствующей величины (1). Известно, что для вычисления коэффициента сдвиговой вязкости необходимо найти автокорреляционную функцию тензора давления:

w n = J I (t) dt,                                                 (1)

где n — коэффициент сдвиговой вязкости, | ( t ) - автокорреляционная функция тензора давления (2),

I ( ' ) = kVT^P ae ( 0 ) ' ^Р ав ( t )) •                                   (2)

где V - объем системы, T - температура системы, Р _ар ( t ) - недиагональная компонента тензора давления (3),

1 N                  N

Рав (t)—y Emivia (t)vie (t) + Zrija (t)Fije (t) ’ где N - число частиц, mi - масса i -й частицы, via (t) - а -я компонента скорости i -й частицы, rija (t) — а -я компонента расстояния между частицами i, j, Fije (t) - сила, действующая между частицами i,j.

В формуле (2) проводится усреднение по ансамблю. Для получения качественного усреднения необходимо проводить расчет для большого количества (> 10 000) различных исходных конфигураций. Подготовка и расчет такого набора независимых конфигураций занимает существенное вычислительное время, поэтому для оптимизации временных затрат была выбрана следующая схема. Проводится расчет одной исходной конфигурации с количеством шагов интегрирова-

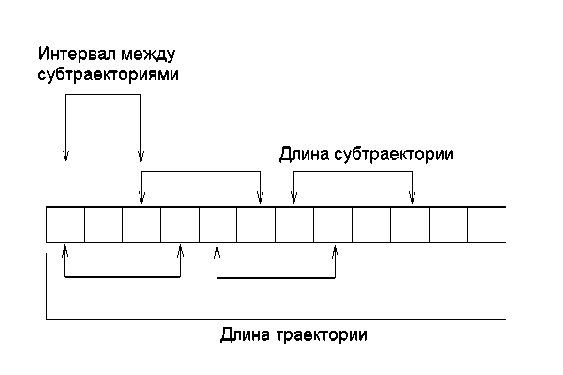
Рис. 1. Схема построения автокорреляционной функции

ния, равным 10 000 000 (шаг интегрирования уравнений движения – 0,001 пс). Далее из всей полученной траектории через каждые 100 шагов выбираются субтраектории длиной 1 000 000 шагов (рис. 1). Каждая из них считается независимой и участвует в построении автокорреляционной функции. Таким образом, получаем 90 000 траекторий для получения среднего по ансамблю. Для улучшения качества автокорреляционной функции выполнялся расчет от 40 до 160 исходных конфигураций.

Расчеты, в которых непосредственно получался тензор давления, проводились в NVT ансамбле. Сред- нее давление было близко к нулю. К кубической ячейке с 2000 атомов железа, взаимодействую- щих посредством ЕАМ потенциала [4], были приложены периодические граничные условия. Ис- ходные конфигурации были получены двумя способами. Первый способ

• 1.    Построение одной конфигурации из 250 частиц для твердой фазы.

• 2.    Нагревание до 2500 К полученной конфигурации.

• 3.    Постепенное охлаждение с запоминанием конфигураций при требуемых для исследо-

• вания температурах.

• 4.    Репликация конфигураций в каждом направлении дважды (2х2х2); таким образом, получаем по одной конфигурации из 2000 частиц для заданной температуры.

• 5.    Для каждой температуры многократно пересоздаем скорости (из нормального распределения) и проводим уравновешивание; таким образом, получаем требуемое количество конфигураций для каждой температуры.

Второй способ

• 1.    Построение требуемого количества конфигураций из 2000 частиц для твердой фазы.

• 2.    Нагревание до 2200 К каждой конфигурации.

• 3.    Постепенное охлаждение с запоминанием конфигураций при требуемых для исследования температурах.

Результаты моделирования

Молекулярно-динамический расчет проводился для температур из интервала 1650–2100 К. Температура плавления чистого железа составляет около 1812 К, следовательно, интервал 1650– 1812 К соответствует переохлажденной жидкости. Для верификации расчета была получена плотность жидкого железа в МД модели. Результат с известными экспериментальными данными изображен на рис. 2. При температурах, выше точки плавления, МД значения плотности пре- имущественно лежат в пределах области разброса экспериментальных данных [10, с. 144]. Виден

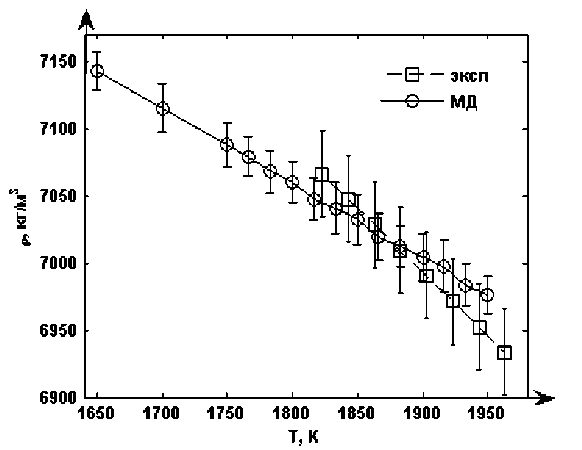
Рис. 2. Температурная зависимость плотности жидкого железа: квадратные маркеры – эксперимент [10], круглые – МД расчет

различный наклон функций плотности. Хорошее совпадение численных значений плотности свидетельствует о пригодности выбранного потенциала [4] и отсутствии ошибок в МД расчете.

Коэффициент сдвиговой вязкости (рис. 3) рассчитан для двух наборов конфигураций, как описано в методике расчета. Как для первого набора, так и для второго есть области плавного и скачкообразного изменения вязкости. Интервал температур от 1766 до 1816 К соответствует переохлажденной жидкости. Значения вязкости здесь изменяются немонотонно, причем очень высок разброс значений. Это сигнализирует о возможной нестабильности внутренней структуры расплава в этой области. Значения вязкости для первого набора получены с большим усреднением (160 конфигураций), тем не менее провал на функции вязкости остается хорошо заметным. Ниже температуры 1750 К вязкость изменяется плавно, что скорее всего указывает на плавное изменение параметров структуры. Выше температуры плавления в каждом из наборов конфигураций наблюдается участок (1833–1883 К – набор 1, 1816–1850 К – набор 2) с плавным изменением вязкости. Далее (до 1950 К) в каждой из зависимостей наблюдаются скачкообразные изменения вязкости, а также почти горизонтальные участки. Это сигнализирует об интенсивном изменении

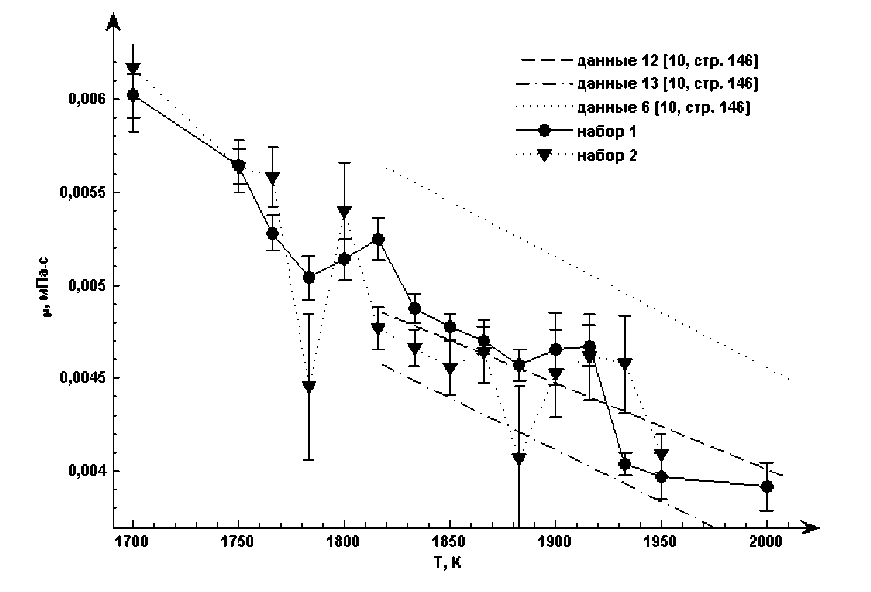
Рис. 3. Температурная зависимость вязкости: круглые маркеры – набор конфигураций 1; треугольные – набор 2; линии без маркеров – экспериментальные данные (см. легенду)

структуры в этом интервале температур, что отмечалось во множестве экспериментальных работ

• [1] . Одинаковое поведение вязкости в этом интервале для рассмотренных наборов указывает на

  

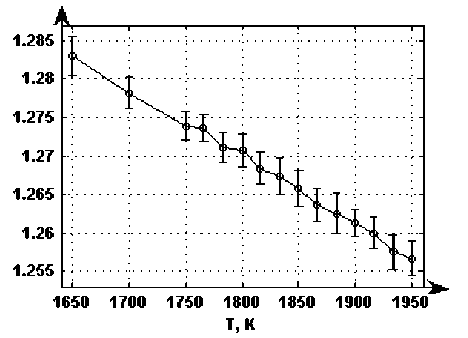
  Рис. 4. Высота второго пика парной корреляционной функции

  
  

существование определенной структуры, обусловливающей обнаруженный характер температурной зависимости. Простое косвенное подтверждение изменения структуры можно найти в изменении высоты второго пика парной корреляционной функции с температурой (рис. 4). В указанных выше интервалах наблюдается немонотонное или резкое изменение высоты пика в сторону увеличения, что говорит о существовании упорядочения внутренней структуры. Это также подтверждает связь внутренней структуры и поведения вязкости.

Основное различие исследованных наборов конфигураций заключается в смещении интервалов с особенностями. Такое различие объясняется отличающимися условиями формирова- ния исходных моделей, однако явная связь между условиями образования конфигураций и видом вязкости пока остается неясной.

Также на рис. 3 показаны некоторые экспериментальные результаты. Полученные значения вязкости лежат между экспериментальными кривыми, что свидетельствует о пригодности используемого потенциала [4] для расчета вязкости жидкого железа вблизи точки плавления.

Выводы

В этой работе применен метод молекулярной динамики с соотношением Грина–Кубо для изучения температурной зависимости вязкости жидкого железа. Для построения модели был использован потенциал погруженного атома, разработанный Менделевым и др. [4]. Показано, что этот потенциал корректно воспроизводит как плотность, так и вязкость жидкого железа. Обнаружены особенности зависимости вязкости от температуры: скачкообразные изменения и области медленного изменения вязкости (горизонтальные участки). Наиболее вероятной причиной этих особенностей предполагается наличие упорядочения в структуре и переход от одного упорядочения к другому. Более строгое обоснование этого предположения должно быть связано с исследованием структуры моделей и соотнесением её с характером изменения вязкости.

Работа поддержана грантом РФФИ № 09-03-00584.