Вклад примесных ионов в пространственно-временное распределение локального электрического поля в нематической жидкокристаллической ячейке

В работе устройств, основанных на электрооптическом переключении жидких кристаллов (ЖК), как правило, предполагается, что электрическое поле внутри слоя жидкого кристалла равно внешнему электрическому полю. Однако примесные ионы в ЖК-слое оказывают существенное влияние на динамику электрооптического переключения и на параметры/характеристики ЖК устройств, а также могут стать причиной различных негативных эффектов (мерцание, залипание изображения, изменение времени электрооптического переключения) [1]. Кроме того, примесные ионы могут приводить к таким нежелательным последствиям для ЖК-устройств, как электрогид-родинамическая нестабильность [2-5].

В ряде работ было показано, что необходимо рассматривать электрическое поле внутри ЖК-слоя как результат перераспределения внешнего управляющего поля между компонентами ЖК-ячейки [6, 7]. В данных работах было доказано, что форма, амплитуда и спектральный состав электрического поля внутри ячейки существенно отличается от внешнего приложенного электрического поля, что оказывает влияние на форму электрооптического переключения данных ячеек [8-10].

Для расчета влияния ионов на характеристики ЖК-ячеек [11, 12] была предложена упрощенная дрейфовая модель переноса ионов в ЖК в приближении малого диффузионного тока, и исследовано влияние примесных ионов на динамику переключения ЖК под воздействием постоянного электрического поля. Было доказано перераспределение приложенного напряжения между слоем ЖК, обусловленное накоплением ионов на границе блокирующего полимерного слоя.

В то же время в случае переменного электрического поля исследовано влияние примесных ионов на формирование двойных электрических слоев [13-15], поляризацию пространственного заряда [16, 17], а также процессы генерации/рекомбинации ионов [18-20]. Основываясь на модели Пуассона–Нернста–Планка, в предположении малого приложенного синусоидального напряжения (V < B^— , e — элементарный заряд, kB - постоянная Больцмана, z - валентность ионов, ze

T - температура [21]), были рассчитаны комплексные спектры диэлектрической проницаемости с учетом влияния ионных примесей [22, 23] . В рамках данной модели предполагается, что диэлектрическая проницаемость постоянна, так как приложенное электрическое напряжение существенно меньше перехода Фредерикса ( V_th ). Данное упрощение не выполняется в случае больших приложенных электрических напряжений ( У>У_Л ), так как из-за пространственновременного переключения директора жидкого кристалла необходимо учитывать анизотропию диэлектрической проницаемости ЖК и ее вклад в нелинейные диэлектрические свойства ЖК-ячеек.

Цель данной работы - моделирование вклада примесных ионов и анизотропии диэлектрической проницаемости нематического жидкого кристалла (НЖК) в пространственно-временное распределение директора и локального электрического поля в ячейке, управляемой синусоидальным электрическим сигналом с амплитудой, превышающей порог Фредерикса.

Расчет локального электрического поля в НЖК-ячейке

В данной работе используется одномерная модель, описывающая планарноориентированную ЖК-ячейку, заполненную нематическим жидким кристаллом. Предполагается, что в объеме жидкого кристалла содержатся только одновалентные ионы.

Для построения пространственно-временного распределения концентрации p(x,t) положи тельных и n (x,t) отрицательных ионов, а также напряженности локального электрического поля

E ( x,t ) применялась система уравнений Пуассона-Нернста-Планка [24-26]: д p ( x, t )_   д J p ( x , t )

д t   “     dx   ’

д n (x, t)   д Jn (x, t)

д t         дx    ’ где Jp (x,t) и Jn (x,t) - плотности потока положительных и отрицательных ионов.

В рамках данного подхода предполагалось отсутствие конвективных течений ЖК, поэтому можно записать, что каждый из токов Jp (x,t) и Jn (x,t) состоит из дрейфового и диффузионно- го слагаемых:

J p ( x , t ) = e ^ p p ( x , t ) E ( x , t ) - eD p

д p ( x , t ) д x

J_n ( x , t ) = e ^ n n ( x , t ) E ( x , t ) + eD_n

д n ( x , t )

дx   ’

д E ( x , t ) д x

e

^o^ (t)

( p ( x , t ) - n ( x , t ) ) ,

где D_n,D_p - коэффициенты диффузии отрицательных и положительных ионов, p_n,р_p - подвижности отрицательных и положительных ионов, s - диэлектрическая проницаемость ЖК. Полагается, что коэффициенты диффузии и подвижности ионов являются постоянными и не зависят от приложенного электрического напряжения, а также равны для положительных и отрицательных ионов D_n = D_p = D_n , _p и д , = д _p = д _п , _p . Соотношение Эйнштейна между коэффициентами диф-

^Dn , p фузии и подвижностями положительных и отрицательных ионов: д = ——

•

^{, p    k}B^T

В качестве начальных и граничных условий предполагается, что начальные концентрации положительных и отрицательных ионов равны между собой и распределены равномерно по ячейке. В данной модели считается, что отсутствуют электрохимические реакции на управляющих электродах, которые являются блокирующими:

J p ( 0, t ) = J p ( d , t ) = 0,                                         (6)

J n ( 0, t ) = J n ( d , t ) = 0,                                           (7)

где d – толщина ячейки.

В дальнейших расчетах к электродам приложено синусоидальное электрическое напряжение V (t ) = V)sin (at) с амплитудой V0 = 2 В, превышающей пороговое напряжение Фредерикса для большинства НЖК (напр. смеси E7 [27]) и частотой v = — = 1 Гц, где a - циклическая частота. 2п

Выбор синусоидального сигнала обусловлен тем, что в дальнейшем полученные результаты будут использованы для получения комплексного спектра нелинейной диэлектрической проницаемости.

Расчет динамики переключения директора НЖК

В данной работе рассматривается планарно-ориентированный НЖК (анизотропия диэлектрической проницаемости As >  0), заключённый в ячейку, состоящую из двух стеклянных подложек с нанесенными на них прозрачными электродами (например, индий оловянный оксид – ITO). Для ориентации НЖК на прозрачные электроды обычно наносится полимерный ориентирующий слой, натертый в одном направлении. Схематическое изображение НЖК ячейки показано на рис. 1, а .

а )

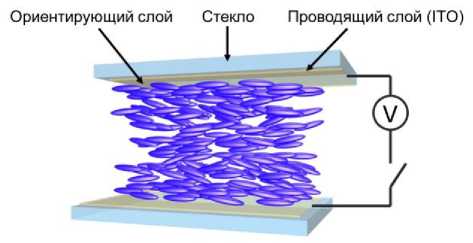
Рис. 1. Схематическое представление ЖК-ячейки, заполненной нематиком: а) приложенное электрическое напряжение V = 0, б) V * 0

б )

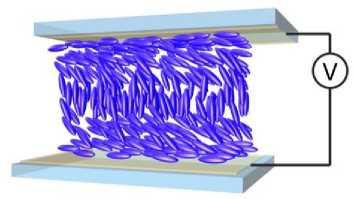
При моделировании предполагалось, что энергия сцепления на ориентирующих слоях является бесконечно большой, а угол преднаклона директора НЖК на поверхности ориентирующего слоя полагался равным 0tilt = 1°. В рамках данного предположения во внешнем электрическом поле директор НЖК не меняет своей ориентации около полимерного слоя (см. рис. 1, б).

Для исследования динамики переключения молекул НЖК используется уравнение Эйлера– Лагранжа:

5 f д _Af f V_rf

ЗӨ  дӨ  дx[дӨ ) Ү дt ’ где f – плотность свободной энергии, являющаяся суммой электрической и упругой частей: f = fупр + fэл , γ – вращательная вязкость ЖК, θ – угол между директором и нормалью к поверхности ячейки.

Ниже приведены формулы для электрической и упругой частей плотности свободной энергии:

Л л = ^{- 1 s} 0 ^{As E} 2 ^sin2 ( ^{Ө (} x ) ) ,

fупр =1 ^ncos2(Ө(x))[df] +1K33sin2(Ө(x))[d^] , 2              [ dx J 2              [ dx J где K11, K33 - модули упругости Франка, £0 - электрическая постоянная, Лs = s — £± — анизо- тропия относительной диэлектрической проницаемости.

Минимизация плотности свободной энергии приводит к уравнению Эриксена–Лесли:

( K J cos² ( Ө ( x ) ) + K з sin² ( Ө ( x ) )) d- ^ + - ( K 3 - K J sin ( 2 Ө ( x ) ) | — | + - A ^ sin ( 2 Ө ( x ) ) E ² = ү — . (11) dx 2   2                       V dx J 2                     dt

В общем случае модули упругости Франка НЖК не равны друг другу, что может привести к нелинейности и отсутствию симметрии при переориентации директора. Уравнение (11) можно упростить, приравняв K 33 = K ₁₁, для исключения нелинейного вклада переориентации ЖК.

Определение эффективной диэлектрической проницаемости

Поскольку молекулы НЖК анизомерны, то его диэлектрическая проницаемость вдоль директора (£||) и в направлении, перпендикулярном к нему (s± ), существенно разные. В связи с этим из-за переориентации молекул ЖК под действием внешнего электрического поля происходит изменение диэлектрической проницаемости вдоль направления приложенного поля. Из-за неоднородной по пространству ориентации директора можно ввести эффективную диэлектрическую проницаемость, определенную как среднюю диэлектрическую проницаемость по пространству вдоль выделенного направления [28, 29]:

d

£ t ) = —1 £ _± + A £ sin² ( Ө ( x , t ))) dx                             (12)

d ₀

Около ориентирующего слоя предполагается, что ориентации директора НЖК не изменяется под действием приложенного электрического поля из-за бесконечности энергии сцепления. В то же время из-за малости толщины данного приповерхностного слоя его вкладом в эффективную диэлектрическую проницаемость можно пренебречь.

Компьютерное моделирование

Для моделирования динамики пространственно-временного распределения концентрации примесных ионов, электрического поля и угла наклона директора НЖК система уравнений (1)– (5), (11) и (12) численно решалась в пакете MATLAB с использованием итерационного метода конечных разностей.

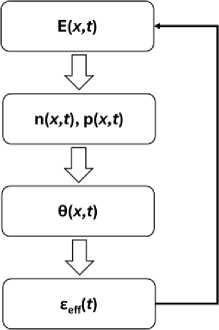
Рис. 2. Блок-схема алгоритма расчета динамики переключения ЖК

Таблица 1

Параметры смеси Е7

K 11 , пН	11
K 33 , пН	18
A £	11
ү , Па^с	0,234
£ 1	6
£ ll	17
Dp , n ,м2/с	1 - 10 - 11

Графический алгоритм расчета рассматриваемой модели представлен на рис. 2. На первом

этапе моделируется распределение электрического поля в ячейке, на втором этапе рассчитывается распределение концентраций положительных и отрицательных ионов, далее следует расчет распределения угла наклона директора молекул НЖК и в конечном итоге рассчитывается временная зависимость эффективной диэлектрической проницаемости ЖК. При расчете использовались материальные параметры НЖК смеси E7 (табл. 1), а толщина ячейки предполагалась равной 6 мкм.

Гавриляк А.М., Гавриляк М.В., Вклад примесных ионов в пространственно-временное Боронин В.А., Подгорнов Ф.В. распределение локального электрического поля...

Кроме того, при расчете предполагалась, что отсутствуют какие-либо дефекты текстуры НЖК, а температура оставалась постоянной и равной 298 К, таким образом материальные параметры не меняются.

Результаты и обсуждение

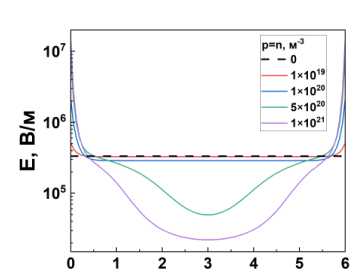
По результатам численного решения систем уравнений (1)-(5), (11) и (12), в приложенном электрическом поле примесные ионы, присутствующие в жидком кристалле, концентрируются около электродов, что влияет на перераспределение напряженности электрического поля внутри ячейки (рис. 3). Из графиков на данном рисунке видно, что увеличение концентрации ионов от n = p = 1 x 10 19 м ^{- 3} до 1 х 10²¹ м ^{- 3} приводит к уменьшению напряженности электрического поля в середине ячейки, а в области около электродов она увеличивается более чем на порядок. Так, например, при концентрации 1 x 10²¹ м ^{- 3} значение напряженности электрического поля в центре уменьшилось до E = 22,1 кВ/м. При концентрации примесных ионов, не превышающей n = p <  1 x 10 19 м ^{- 3}, в центре ячейки не наблюдается пространственное перераспределение

х, мкм

Рис. 3. Пространственное распределение напряженности локального электрического поля в НЖК ячейке при разных значениях концентраций ионов при t = т/ 4 , где т - период колебаний; Частота и амплитуда приложенного синусоидального сигнала v = 1 Гц и V _o = 2 В

соответственно

электрического поля, а его напряженность равна E = 32,7 кВ/м.

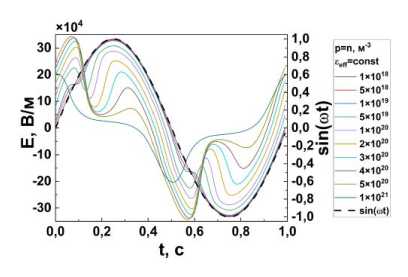
Рис. 4. Временная зависимость напряженности локального электрического поля в середине ячейки x = d/ 2 (в течение одного периода приложенного сигнала) при разных значениях концентрации примесных ионов. Частота и амплитуда приложенного синусоидального сигнала v = 1 Гц и V _o = 2 В соответственно

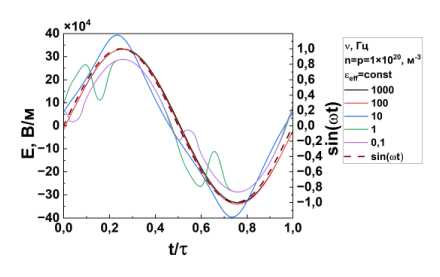
Рис. 5. Зависимость напряженности локального электрического поля (в середине ячейки x = d/ 2) от нормированного на период времени. Данный график взят за один период приложенного поля, концентрация примесных ионов 1x 1021 м-3 , амплитуда приложенного синусоидального напряжения Vo = 2 В

При увеличении концентрации ионов временное распределение напряженности поля в середине ячейки принимает несинусоидальный вид (рис. 4), который проявляется в виде дополнительного пика в начале каждого полупериода. Величина пика растет при увеличении концентрации. Также амплитуда напряженности поля начинает уменьшаться при концентрации 5 x 1019 м-3 . При концентрации 1x 1021 м-3 электрическое поле, создаваемое ионами Eион , имеет доминирующий вклад в локальное электрическое поле Eлок ячейки. Здесь мы предполагаем, что Eион , Eлок и приложенное электрическое поле Епр = V/d связанны соотношением

E лок

= E пр

+ E ион •

Временная зависимость локального электрического поля E лок значительно отличается от формы приложенного сигнала E пр .

Отклонение динамики электрического поля в середине ячейки в присутствии большой концентрации ионов имеет частотную дисперсию (рис. 5). Таким образом, для низких частот (0,1 Гц и 1 Гц) сигнал значительно отклоняется от синусоидальной формы, проявляя дополнительные пики, которые отсутствуют при частотах более 100 Гц. Данное поведение электрического поля в ячейке можно объяснить характерным временем электродиффузии ионов, при котором ионы достигают противоположного электрода и начинают накапливаться на нем.

Из рис. 5 также видно, что при низких частотах ( v <  1 Гц) максимум напряженности локального электрического поля достигается раньше, чем при высоких частотах, что указывает на существенные различия в динамике перераспределения поля в зависимости от частоты приложенного электрического напряжения.

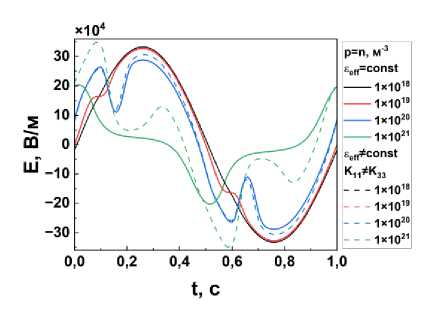
Рис. 6. Сравнение временных зависимостей напряженности локального электрического поля в середине ЖК-ячейки (за один период приложенного электрического синусоидального сигнала) при различных концентрациях примесных ионов, с учетом (пунктирные линии) и без учета (сплошные линии) зависимости эффективной диэлектрической проницаемости от ориентации директора НЖК для K ! * К₃₃

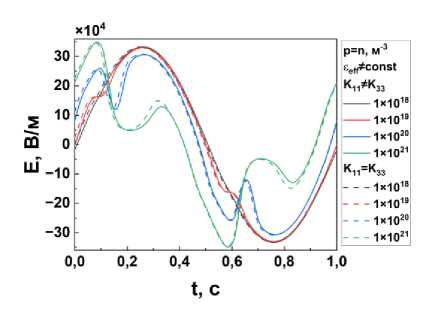
Рис. 7. Сравнение временных зависимостей напряженности локального электрического поля в середине ЖК-ячейки (за один период приложенного сигнала) при разных значениях концентрации примесных ионов с учетом эффективной диэлектрической проницаемости е_е$ * const в двух случаях: при различных K 11 * K 33 и одинаковых K == K₃₃ модулях упругости Франка

На рис. 6 представлено сравнение временных зависимостей напряженности локального электрического поля в центре ЖК-ячейки ( x = d 2 ) с учетом и без учета изменения эффективной диэлектрической проницаемости ε_eff от угла наклона директора НЖК при различных концентрациях примесных ионов. При концентрации ионов n = p = 1 х 10¹⁸ м ^{- 3} зависимость напряженности локального электрического поля от времени не отличается от формы приложенного сигнала, но при увеличении концентрации можно наблюдать изменение формы функциональной зависимости кривой напряженности локального электрического поля. Как видно из данного графика, концентрация примесных ионов влияет на спектральный состав локального электрического поля, что должно приводить к нелинейности электрооптического отклика НЖК ячейки.

Учет влияния переориентации директора НЖК на эффективную диэлектрическую проницаемость показал, что при больших концентрациях ионов n, p >  1 х 10²¹ м ^{- 3} происходит увеличение амплитуды первой гармоники при неизменности амплитуд высших гармоник.

Моделирование локального электрического поля в ячейке при различных параметрах жидкого кристалла в случае различных K 11 * K 33 и одинаковых K 11 = K 33 модулях упругости Франка (рис. 7) показало, что в обоих случаях присутствует значительная нелинейность электрического поля. Наибольшее влияние коэффициентов упругости Франка на распределение локального электрического поля происходит при концентрации ионов n , p >  1 х 10²¹ м ^{- 3}, что в целом согласуется с результатами, представленными на рис. 6, и связанно с перерасчетом эффективной диэлектрической проницаемости.

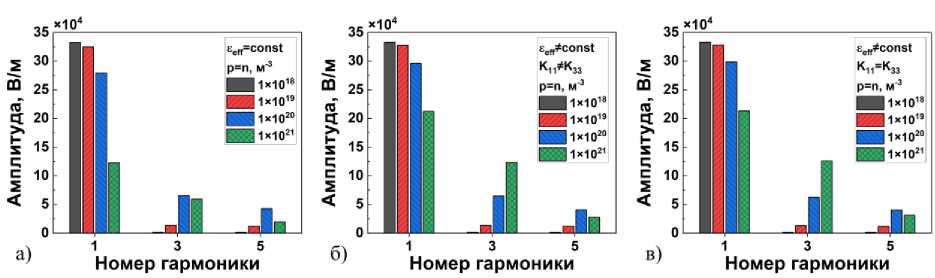
Рис. 8. Зависимость амплитуды локального электрического поля 1-й, 3-й и 5-й гармоник от концентрации примес-

ных ионов в случае а) постоянной эффективной диэлектрической проницаемости е^ = const , б) эффективной диэлектрической проницаемости, зависящей от ориентации директора при K 11 * K 33 , в) K 11 = K 33

Примесные ионы в ЖК-ячейке вызывают пространственные искажения электрического поля, что приводит к изменению его спектрального состава. Для количественного анализа вклада высших гармоник в локальное электрическое поле удобно использовать диаграммы, полученные с помощью быстрого преобразования Фурье, отражающие зависимость амплитуды высших гармоник от концентрации примесных ионов (рис. 8). Из данных диаграмм следует, что основная гармоника вносит доминирующий вклад во временную зависимость электрического поля. С увеличением концентрации примесных ионов основная гармоника уменьшается, однако в то же время наблюдается рост амплитуды 3-й и 5-й гармоник, что указывает на усиление нелинейных эффектов. Влияние учета анизотропии ЖК на амплитуду электрического поля наиболее значимо при больших концентрациях (n, p > 1 х 1021 м-3), независимо от того, равны ли друг другу коэффици енты упругости Франка (K х = K3 ) или нет (Kj* K3). Отсутствие четных гармоник свидетельствует о центросимметричности исследуемой системы относительно знака подаваемого электрического напряжения.

Для количественной оценки отклонения формы локального электрического поля от идеальной синусоиды рассчитаны коэффициенты гармонических искажений ( K ):

K

E 2 + E 3 + E 2 + ... + E n

Г             E 1

,

где E – амплитуда n -й гармоники электрического поля.

Таблица 2

Коэффициенты гармонических искажений при различных концентрациях ионных примесей для случаев постоянной эффективной диэлектрической проницаемости е^ = const и эффективной диэлектрической проницаемости, зависящей от ориентации директора при Kх * К33 и K j = K33

	n , p = 1018 м - 3	n , p = 1019 м 3	n , p = 1020 м - 3	n , p = 1021 м - 3
E eff = const	0,815 %	6,402 %	29,155 %	50,879 %
E eff * const, K 11 * K 3 3	0,790 %	6,275 %	26,882 %	60,464 %
E eff * const, K 11 = K 3 3	0,767 %	6,132 %	25,943 %	61,414 %

Анализ коэффициентов гармонических искажений показал (см. табл. 2), что при концентрации примесных ионов n,p <  1 х 10²⁰ м ^{- 3} отклонение от синусоидального сигнала уменьшается при учете эффективной диэлектрической проницаемости, а также с исключением нелинейностей, вызванных разницей в модулях упругости Франка K 11 * K 33 . Данный эффект отчетливо выражен при концентрации примесных ионов n , p = 1 х 10²⁰ м ^{- 3}, где коэффициент гармонических искажений уменьшился более чем на 3 %. Но при больших концентрациях n , p >  1 х 10²¹ м ^{- 3} наблюдается обратный эффект. При учете эффективной диэлектрической проницаемости при больших концентрациях примесных ионов амплитуда основной гармоники также увеличивается.

Моделирование динамики переключения директора НЖК

Результаты моделирования показали, что перераспределение локального электрического поля приводит к изменению динамики переориентации директора ЖК в присутствие ионов. На рис. 9 представлены результаты численного моделирования пространственно-временного распределения угла наклона молекул ЖК, рассчитанные для двух случаев: а) в отсутствие и б) в присутствии примесных ионов. Включение в моделирование ионов приводит к перераспределению электрического поля внутри ячейки и уменьшению максимального угла наклона. Кроме того, наблюдаются изменения в характере пространственно-временной динамики переориентации молекул.

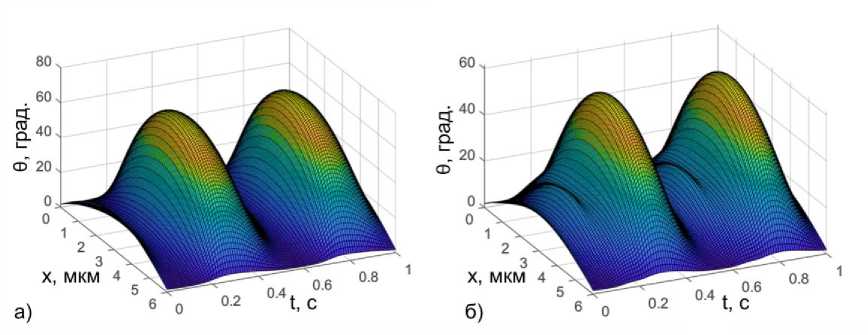
Рис. 9. Пространственно-временное распределение угла наклона директора НЖК: а) без учета ионов и б) при n,p = 1x1020 м-3 . Частота и амплитуда приложенного синусоидального сигнала v = 1 Гц и Vo = 2 В соответст

венно; K ^ к₃₃

Возникновение дополнительного пика в напряженности электрического поля также отражается и на возникновении дополнительного максимума в распределении угла наклона директора при концентрациях выше 5 x 10¹⁹ м ^{— 3} . Как показано на рис. 10, при увеличении начальной концентрации ионов максимальное значение, до которого переориентируются молекулы     ЖК,     уменьшается:     при

18 — 3

n = p = 1 x 10 м максимальный угол переориентации директора 6 *_max = 68,2 ° , а при n = p = 1 x 10²⁰ м ^{— 3} 6 *_max = 61,5 ° . Таким образом, рост концентрации примесных ионов приводит к уменьшению максимального угла переориентации директора, это может быть свя-

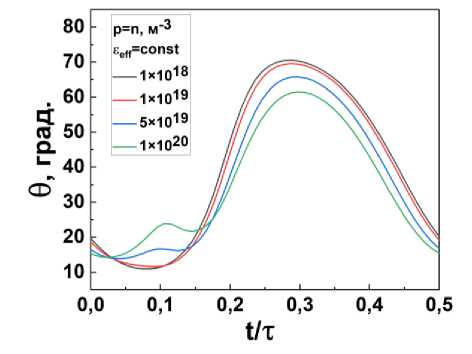
Рис. 10. Динамика переориентации директора НЖК в середине ячейки ( х = d /2) за половину периода при разных значениях концентраций ионов

зано с ослаблением локального электрического поля внутри ячейки.

В данной статье исследованы причины нелинейности локального электрического поля в планарно-ориентированной нематической жидкокристаллической ячейке с блокирующими электродами в присутствии примесных ионов.

Используя систему уравнений Пуассона–Нернста–Планка и нелинейное уравнение Эриксена–Лесли, численно рассчитали влияние ионных примесей и динамики переориентации директора ЖК на локальное электрическое поле в ячейке, заполненной НЖК смесью Е7, при приложении внешнего синусоидального электрического напряжения, амплитуда ( V 0 = 2 B) которого существенно больше перехода Фредерикса ( V th ~ 0,9 В).

Результаты компьютерного моделирования показали, что существуют две причины нелинейности, приводящие к искажению синусоидальной формы локального электрического поля в НЖК: 1) нелинейная динамика переключения директора НЖК, 2) пространственновременная неоднородность распределения примесных ионов. Было установлено, что учет эффективной диэлектрической проницаемости ЖК вносит дополнительный вклад в нелинейное поведение локального электрического поля, особенно при высоких концентрациях ионов. Частотный анализ временной зависимости локального электрического поля показал, что вклад, вызванный нелинейностью динамики переключения директора ЖК, существенно меньше, чем вклад неоднородности перераспределения примесных ионов в приложенном электрическом поле. Показано, что кривые напряженности принимают нелинейный вид только при низких частотах < 100 Гц, что связано с процессами электродиффузии и перераспределения ионов внутри ячейки.

Также показано влияние нелинейности локального электрического поля в присутствии примесных ионов на динамику переориентации директора ЖК, что позволяет более точно предсказывать возможные отклонения в электрооптическом отклике устройств на основе жидких кристаллов.

Исследование выполнено за счет гранта Российского научного фонда No 23-13-00045,

• 1.    Garbovskiy, Y. Kinetics of Ion-Capturing / Ion-Releasing Processes in Liquid Crystal Devices utilizing Contaminated Nanoparticles and Alignment Films / Y. Garbovskiy // Nanomaterials. – 2018. – Vol. 8, Iss. 59. – P. 1–11.

• 2.    High Contrast Switching of Transmission due to Electrohydrodynamic Effect in Stacked Thin Systems of Liquid Crystals / S.V. Serak, U. Hrozhyk, J. Hwang et al. // Applied Optics. – 2016. – Vol. 55, Iss. 30. – P. 8506.

• 3.    Numerical Prediction of Transient Electrohydrodynamic Instabilities under an Alternating Current Electric Field and Unipolar Injection / C.-T. Zhou, Z.-Z. Yao, D.-L. Chen et al. // Heliyon. – 2023. – Vol. 9, Iss. 1. – P. e12812.

• 4.    Nonlinear Electro-Hydrodynamics of Liquid Crystals / E.S. Pikina, A.R. Muratov, E.I. Kats, V. V. Lebedev // Journal of Experimental and Theoretical Physics. – 2023. – Vol. 137, Iss. 1. – P. 114– 124.

• 5.    Беляев, В.В. Физические методы измерения коэффициентов вязкости нематических жидких кристаллов / В.В. Беляев // Успехи физических наук. – 2001. – Т. 171, № 3. – C. 267.

• 6.    Direct Current Electric Conductivity of Ferroelectric Liquid Crystals–Gold Nanoparticles Dispersion Measured with Capacitive Current Technique / A.R. Karaawi, M.V. Gavrilyak, V.A. Boronin et al. // Liquid Crystals. – 2020. – Vol. 47, Iss. 10. – P. 1507–1515.

• 7.    Mesophase Materials as Smart Media for Emerging Pressure Sensors: Capacitive Method of Measurement of DC Conductivity / F.V. Podgornov, M. Gavrilyak, A. Karaawi et al. // Proc. 2018 Global Smart Industry Conference (GloSIC 2018). – 2018. – P. 1–5.

• 8.    Hysteresis Inversion Frequency for V-Shape Electrooptical Switching Controlled by Dynamic Impedance of Ferroelectric SmC* Phase / L.M. Blinov, E.P. Pozhidaev, F.V. Podgornov et al. // Ferroelectrics. – 2002. – Vol. 277. – P. 3–11.

• 9.    Modeling Electrooptical Effects in Ferroelectric Liquid Crystals. 1. Basic Equations and Experimental Tests / S.P. Palto, F.V. Podgornov, W. Haase, L.M. Blinov // Molecular Crystals and Liquid Crystals. – 2004. – Vol. 410. – P. 95–104.

• 10.    Modeling Electrooptical Effects in Ferroelectric Liquid Crystals. 2. V-Shape Switching in the SmC* Phase / L.M. Blinov, S.P. Palto, E.P. Pozhidaev et al. // Molecular Crystals and Liquid Crystals. – 2004. – Vol. 410. – P. 105–115.

• 11.    Molecular Reorientation Dynamics due to Direct Current Voltage-Induced Ion Redistribution in Undoped Nematic Planar Cell / P. Pagliusi, B. Zappone, G. Cipparrone, G. Barbero // Journal of Applied Physics. – 2004. – Vol. 96, Iss. 1. – P. 218–223.

• 12.    Palomares, L.O. Optical Response of a Nematic Sample Submitted to a Periodic External Electric Field: Role of the Ionic Impurities / L.O. Palomares, J.A. Reyes, G. Barbero // Physics Letters A. – 2004. – Vol. 333, Iss. 1–2. – P. 157–163.

• 13.    Rybakov, D.O. Electrical Double Layers and Their Effect on the Low-Frequency Dielectric Permittivity of 4-n-Pentyl-4’-Cyanobiphenyl (5СВ) / D.O. Rybakov, V.V. Belyaev // Liquid Crystals and Their Applications. – 2018. – Vol. 18, Iss. 4. – P. 40–47.

• 14.    Беляев, Б.А. Исследование электрофизических характеристик границы электрод – жидкий кристалл методом импедансной спектроскопии / Б.А. Беляев, Н.А. Дрокин // Физика твердого тела. – 2015. – Т. 57, № 1. – С. 170–175.

• 15.    Sawada, A. Modeling of Electrode Polarization for Electrolytic Cells with a Limited Ionic Adsorption / A. Sawada // Physical Review E. – 2013. – Vol. 88, Iss. 3. – P. 032406.

• 16.    Sawada, A. Electrode Process of Mobile Ions in Generating Space-Charge Polarization / A. Sawada, T. Manaka // Physical Review E. – 2024. – Vol. 109, Iss. 3. – P. 034802.

• 17.    Probing Modulated Liquid Crystal Media with Dielectric Spectroscopy / M.P. Rosseto, R.R. Ribeiro de Almeida, E.K. Lenzi et al. // Journal of Molecular Liquids. – 2023. – Vol. 390. – P. 122943.

• 18.    Ganea, C. P. Effects of the Ionic Association-Dissociation and Adsorption-Desorption on the Space Charge Polarization: A new theoretical approach / C. P. Ganea // European Physical Journal Plus. – 2014. – Vol. 129, Iss. 10. – P. 238.

• 19.    Ganea, C. P. New Approach of the AC Electrode Polarization during the Measurements of Impedance Spectra / C.P. Ganea // Romanian Journal of Physics. – 2012. – Vol. 57. – P. 664–675.

• 20.    MacDonald, J.R. Utility of Continuum Diffusion Models for Analyzing Mobile-Ion Immittance Data: Electrode Polarization, Bulk, and Generation-Recombination Effects / J. R. MacDonald // Journal of Physics: Condensed Matter. – 2010. – Vol. 22, Iss. 49. – P. 495101.

• 21.    Bazant, M.Z. Diffuse-charge Dynamics in Electrochemical Systems / M. Z. Bazant, K. Thornton, A. Ajdari // Physical Review E. – 2004. – Vol. 70, Iss. 2. – P. 021506.

• 22.    Frequency-Dependent Dielectric Permittivity in Poisson–Nernst–Planck Model / M.P. Rosseto, L.R. Evangelista, E.K. Lenzi et al. // Journal of Physical Chemistry B. – 2022. – Vol. 126, Iss. 34. – P. 6446–6453.

• 23.    Khazimullin M.V. Influence of Dielectric Layers on Estimates of Diffusion Coefficients and Concentrations of Ions from Impedance Spectroscopy / M.V. Khazimullin, Y.A. Lebedev // Physical Review E. – 2019. – Vol. 100, Iss. 6. – P. 1–15.

• 24.    Barbero, G. Effective Dielectric Constant of Electrolytes / G. Barbero, I. Lelidis // Journal of Applied Physics. – 2014. – Vol. 115, Iss. 19. – P. 194101.

• 25.    Derfel, G. Numerical Study of Ionic Current in Dielectric Liquid Layer Subjected to AC Voltage / G. Derfel // Journal of Molecular Liquids. – 2009. – Vol. 144, Iss. 1–2. – P. 59–64.

• 26.    Вклад поляризации пространственного заряда в нелинейный спектр диэлектрической проницаемости нематического жидкого кристалла: компьютерное моделирование / М.В. Гаври-ляк, А.М. Гавриляк, В.А. Боронин, Ф.В. Подгорнов // Жидкие кристаллы и их практическое использование. – 2025. – Т. 25, № 1. – С. 62–71

• 27.    Measurement of the Twist Elastic Constant of Nematic Liquid Crystals using Pi-Cell Devices / P. D. Brimicombe, C. Kischka, S. Elston, E.P. Raynes // Journal of Applied Physics. – 2007. – Vol. 101, Iss. 4. – P. 1–8.

• 28.    Shcherbinin, D.P. Electric Method for Studying Reorientation Dynamics of the Nematic Liquid Crystal Director / D.P. Shcherbinin, D.A. Vakulin, E.A. Konshina // Technical Physics. – 2016. – Vol. 61, Iss. 7. – P. 1039–1045.

• 29.    Chen, H.Y. Electrodynamic Behaviour of Nematic Liquid Crystal in a Relaxation Process / H. Y. Chen, K.X. Yang, Z.Y. Lin // Journal of Physics D: Applied Physics. – 2010. – Vol. 43, Iss. 31. – P. 315103.

Поступила в редакцию 14 февраля 2025 г.

Гавриляк Алина Маратовна – аспирант, ассистент, кафедра оптоинформатики, ЮжноУральский государственный университет, г. Челябинск, Российская Федерация, e-mail: , ORCID iD:

Гавриляк Максим Витальевич – ассистент, кафедра оптоинформатики, Южно-Уральский государственный университет, г. Челябинск, Российская Федерация; младший научный сотрудник, лаборатория нелинейной оптики, Институт электрофизики УрО РАН, Екатеринбург, Российская Федерация, e-mail: , ORCID iD:

Гавриляк А.М., Гавриляк М.В., Вклад примесных ионов в пространственно-временное Боронин В.А., Подгорнов Ф.В. распределение локального электрического поля…

Боронин Виктор Александрович – младший научный сотрудник, лаборатория нелинейной оптики, Институт электрофизики УрО РАН, Екатеринбург, Российская Федерация; ассистент, кафедра оптоинформатики, Южно-Уральский государственный университет, г. Челябинск, Российская Федерация, e-mail: , ORCID iD:

Подгорнов Федор Валерьевич – доцент кафедры физики наноразмерных систем, ЮжноУральский государственный университет, г. Челябинск, Российская Федерация, e-mail: , ORCID iD:

Bulletin of the South Ural State University Series “Mathematics. Mechanics. Physics” 2025, vol. 17, no. 2, pp. 69–81

CONTRIBUTION OF IMPURITY IONS TO SPATIAL-TEMPORAL DISTRIBUTION OF LOCAL ELECTRIC FIELD IN NEMATIC LIQUID CRYSTAL CELL

A.M. Gavrilyak1, M.V. Gavrilyak1,2, V.A. Boronin1,2, F.V. Podgornov1

• ¹    South Ural State University, Chelyabinsk, Russian Federation

• ²    Institute of Electrophysics, Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation

Гавриляк А.М., Гавриляк М.В., Вклад примесных ионов в пространственно-временное Боронин В.А., Подгорное Ф.В.распределение локального электрического поля...

Received February 14, 2025

Gavrilyak Alina Maratovna is Post-graduate Student, Assistant, Department of Optoinformatics, South Ural State University, Chelyabinsk, Russian Federation, e-mail: , ORCID iD:

Gavrilyak Maksim Vitalievich is Assistant, Department of Optoinformatics, South Ural State University, Chelyabinsk, Russian Federation; Junior Research Fellow, Laboratory of Nonlinear Optics, Institute of Electrophysics, Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation, e-mail: , ORCID iD:

Boronin Viktor Aleksandrovich is Post-graduate Student, Junior Research Fellow, Laboratory of Nonlinear Optics, Institute of Electrophysics, Ural Branch of the Russian Academy of Sciences, Ekaterinburg, Russian Federation; Assistant, Optoinformatics Department, South Ural State University, Chelyabinsk, Russian Federation, e-mail: , ORCID iD:

Podgornov Fedor Valerievich is Cand. Sc. (Physics and Mathematics), Associate Professor, Physics of Nanoscale Systems Department, South Ural State University, Chelyabinsk, Russian Federation, e-mail: , ORCID iD:

Вестник ЮУрГУ. Серия «Математика. Механика. Физика»

2025, том 17, № 2, С. 69–81