При очень низких ( T <  10 K) температурах в полупроводниках часто реализуются условия, когда основным механизмом рассеяния свободных электронов (дырок) становится рассеяние на нейтральных атомах примеси. Мелкая примесь имеет целый спектр возбужденных s -состояний и если один отщепленный s -уровень примыкает к дну зоны проводимости E C , то возможно резонансное рассеяние носителей тока [1]. В принципе, это позволяет заменить атом мелкой примеси некоторым модельным потенциалом. Для объёмных полупроводников таким модельным потенциалом может быть трехмерная прямоугольная потенциальная яма, для квазидвумерных -двумерная прямоугольная яма.

S -резонансный уровень, локализованный вблизи E C , оказывает существенное влияние на процессы переноса энергии и заряда носителями при различных внешних условиях [2], например, при наличии слабого магнитного поля электронная проводимость невырожденного полупроводника достигает максимума ( T >  1 K, H <  200 Э), причем слабое H -поле учитывается своеобразно - как приращение радиуса резонансного центра [3]. Подход, развитый в работе [3], в принципе позволяет исследовать влияние резонансного рассеяния носителей тока на электронные явления переноса и при условиях классического предела циклотронного резонанса (ЦР). Однако в работах [2, 3] s -резонансный уровень строго фиксирован и имеет статичный характер, что затрудняет зондирование произвольных примесных глубин в условиях классического ЦР. Эта трудность устранена в работе [4], в которой получены формулы для полуширины кривой поглощения ЦР, причем они выражены через длину рассеяния и, следовательно, справедливы для произвольного потенциала примеси конечного радиуса действия. Формулы для времени релаксации также выражены через длины 2D- и 3D рассеяния.

В невырожденных полупроводниках длина волны электрона X ^ 1 / TT и при сверхнизких температурах существенны квантово-статистические поправки. В области температур, соответствующих резонансным глубинам примесного потенциала, можно ограничиться квазиклассиче-ским рассмотрением (см. прим. 1), но и здесь следует учесть статистику. Дело в том, что время релаксации Т есть среднее время свободного пробега, т.е. время между двумя актами рассеяния. Оно определяется длиной свободного пробега и полной скоростью электрона, но не скоростью дрейфа в магнитном поле. Полная скорость зависит от E - кинетической энергии электрона. Тем самым Т = Т (E) . Эта зависимость усложняется в том случае, когда длина свободного пробега также зависит от E . Поэтому для нахождения 5 to =| to - toc | - уширения линии ЦР, как и множества других параметров, необходимо усреднять как т(E) , так и 1 / т(E), а также и другие величины, с учетом функции распределения электронов по энергии. Однако в работе [4] время релаксации, а вслед за этим и полуширина линии поглощения 5 toN d (E) = 1/ т 2 d 3 d (E) лишь оцениваются характерным параметром k = J 2 m * kB T J k (m * — эффективная масса электрона, kB — константа Больцмана). Такой подход, на наш взгляд, является не вполне корректным и требует проведения более детального расчета.

Как следует из классической статистики, нет необходимости, чтобы энергия электрона была близка к резонансному уровню модельного потенциала. Игнорирование этого факта [4] может привести к неточным выводам. Вывод о том, что 5to 3 _d ^ T ^{- 2} [4], сомнителен и требует тщательного анализа. Замена волнового числа тепловым параметром не позволяет учесть более быстрые и более медленные электроны, а ведь именно они формируют хвост распределения Максвелла в области очень низких и высоких температур. Представление о невзаимодействующих электронах также крайне упрощенное [4]. При таком подходе теряет смысл перераспределение энергии между степенями свободы при различных механизмах рассеяния носителей.

В предлагаемой работе производится расчет полуширины кривой поглощения при резонансном рассеянии электронов на нейтральных примесях в квазидвух- и трехмерных полупроводниках путем усреднения с максвелловским весом. Уточняются пределы применимости полученных формул. Частота внешнего электрического поля весьма близка к циклотронной частоте, так что влияние нейтральных примесей, ионов примеси и акустических фононов сводится, как правило, к нарушению (размытию) спектра поглощения, т.е. как если бы не было заряженных и нейтральных примесей, фононов и т.д., то и не было бы уширения. Ясно, что в рамках вычислений, проводимых с использованием формулы Эргинсоя [5], нельзя получить формулу для уширения кривой классического ЦР ( т = const). Анализируются особенности в спектре поглощения.

f m

2 i )

n ²

k

П 2   1 2

---+ ln2

( Y^ka 2 d ,

Y ka 2 d

■ f 3 d ° ( k ) = - 4—1—•    ° з d ( ^k ) = 4 * 1 f3 d ° ( ^k )| 2 =       ^п —ТГ ■     (²)

^{ik +} V ^a 3 d                       ^{1           1} k² + ( 1/ a _{3 d} ) ²

Здесь у = e C, С - постоянная Эйлера, k = 2 m * E h , a 2 d и a3 d - длины двух и трехмерного рассеяния. В области температур, соответствующих резонансным глубинам: a rds = r° X „ Г 2Uo I res 2U° z

X exp I — a у I , a _{3 d} = r ° a у (это и есть размеры волновых функции резонансных уровней)

[4], где r ° A U = U — U

–

res

радиус 2- и 3D модельного потенциала примеси; U ° = h 2/(2 m * r °²), - расстройка потенциала от U res , U — глубина трехмерной (двумерной) ямы.

Если A U >  0 рассеяние происходит на резонансном уровне, при A U <  0 - на виртуальном уровне. Тогда на основе формул (1) и (2) для полуширины линии поглощения Sto = = I to — to _c I м to _C имеем

3 d

3 d

¹          n i ^h _k ^tr

/ —       ,    \ ° ° 3 /7

( •           3 d

^k )/ ^{m x}

3d n i h

*

m

•

(

h

^

^Е 3 d

^def ( A U ) ²

\ к

2 3d п h n i

4 п

к ²

+

h______

Г A U

\ ²

к r ° 2 U ° 7

E

^

4 U 0

/ м 3/2

^{( m} )

E

E ^{+ E} 3 d

^

E

( Ч3/2

^{( m} )

”,     Ee

E

^{3 d} J E + E i 0

^

exp 3 d

J E exp

^^^^^^в

к

(

^^^^^^^

к

E k в T

F I I—

---I 4Ё dE k в T I

4 ( k в T ) ²

---^--r^ X

( m * ) ³"²   3 Ji ( k , T ) ^5,2

3 d

^   2

x exp ( — x )

X             dx =

°    ^{x + E} °

3 d

3 ( m * ) ^3,2 -PTT

^{— Е} ° L ( ^Е ° ) ] .

Здесь n ^{3 d} —

концентрация атомов примеси, измерения показывают что n ^{3 d} <  2 X 1°¹⁵ см ³ [2],

E ° = E ₃ d / k _B T , Е _{3 d} — эффективный резонансный уровень.

L ( ^E ° ) = ^{1 — E} ° exp ( ^E ° ) [ ^— Ei ( ^{— E} ° ) ] ^ Ei ( E ° ) = — J exp⁽ x x ) dx .

^E °

Пользуясь разложением в ряд и асимптотическим выражением для Ei( — Е ° ) можно показать, что [1]

L (Е°) - 1 /е ° — 2/е° + .„      (Е° >>1)^

L (Е °) - 1 + Е °ln Е ° + _     (Е ° >1).(5)

Подставляя (4) и (5) в точную формулу (3) получаем предельные формулы:

А    8^ Л h ² n 3 ^d 12

\Sto3 d ( k)/ - ----;------------ ^ ^T ^       (Е3 d > kв T ) ;

^X          '     3 ( m * )^3Л #в ^{T E} 3 d

/5to3 d ( k )\ - ----------—-i--.       ^ 1 /Tl7,        (E3 d > kв T ) .

'   ³      '      3 ( m • )^3,2 AB T

Муратов Т.Т.                                Вклад резонансного рассеяния носителей заряда в уширение кривой классического циклотронного резонанса...

Как и следовало ожидать, в области «высоких температур» (£3 d « k в T ) влияние резонанс ных центров (на фоне других механизмов рассеяния) на уширение кривой поглощения ЦР исчезающе мало. Аналогичные зависимости получаются и в квантовом пределе ЦР [8]. Отличие состоит лишь в том, что в работе [8] усреднение проводилось на основе равновесной функции распределения в квантующем магнитном поле. Дело в том, что в условиях квантующих H -полей невырожденные электроны расположены на нулевом уровне Ландау, в пределах которого плотность состояний — 1 /ЕЁ; вследствие этой зависимости вместо формулы (3) мы полу чим/ Зю3 d ( k )) —

L(е0)/7 kB T • Соответственно, правомерны и зависимости (6) и (7). При мерно при 2 K на нулевом уровне Ландау можно наблюдать вполне четкий резонанс (Зю —> 0) (см. математическое дополнение). Следовательно, и в классическом пределе ЦР, в определенной области температур и глубин ямы, можно ожидать появления максимума полуширины линии по глощения.

Следует отметить, что под «высокими температурами» мы здесь понимаем область выше области температур, соответствующих резонансным глубинам. Таким образом, профиль полуширины линии поглощения: / Зю ₃Л — T С². Эту асимптотику можно интерпретировать так:

кривая поглощения резонансно уширяется за счет слишком «быстрых» или слишком «медленных» электронов, из-за распределения Максвелла. Из (6) следует, что окрестность абсолютного нуля якобы идеально соответствует ЦР (см. прим. 2). Именно из-за распределения Максвелла и учета слабого взаимодействия между электронами не происходит разогрева электронов. Они успевают дерезонировать, т.е. выбывать из резонанса только путем рассеяния друг на друге, до нарушения закона Ома. Ясно, что в промежутке между двумя ветвями: ^ Зю ₃ d ( k )^ 0 — TT и

(^Зю 3 d

( k)) T

о

1 / TT , как уже отмечалось, где-то должен быть максимум, в противном

случае мы просто не получим кривую, характерную для ЦР (рис. 1). В области температур T > 30 K начинает также давать вклад в уширение рассеяние на акустических фононах Зю3 d ^^ — T3/ 2 [1]. Начиная с T > 17 K необходим учет рассеяния на заряженных примесях, точечных дефектах, дислокациях, границах кристаллитов и т.д., так что полное уширение

^{3 Зю} 3 d ⁽ k )) T °7

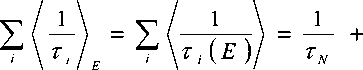
— + т

1 --- +

^Т AL

^Т D

Здесь следует уточнить, что подразумевается под каждым слагаемым: первый член соответствует уширению за счет остатка резонансного рассеяния на нейтральных примесях (асимптотика (7)), второй - за счет рассеяния на ионах примеси, третий обусловлен акустическими фононами. При очень низких температурах достаточно ограничиться (в нашем случае) резонансным рассеянием электронов; асимптотика (6).

Учет акустических фононов (в рамках метода деформационного потенциала) вблизи абсолютного нуля не имеет смысла, так как формула для длины свободного пробега l_AL = A/k _B T

• [1]    при температурах, близких к абсолютному нулю, неприменима. Соответствующий расчет [6] дает для ^ Зю ₃ d ( k )^ две ветви: — T ~ ³'2 и T ¹² (рис. 1),откуда доопределяется асимптотика (7):

T О

ЗЗю 3 d ( k ))       - с 1 T ^- 1/2 + c 2 T 1/2 + c 3 T ³'² + - .                  (7 6)

T ^ о

Оценки показывают, что уширение линии ЦР в объемных образцах можно наблюдать в ИК-диапазоне частот (субмиллиметровый диапазон, T max = 11 K (см. прим. 2)).

В том случае, когда столкновения носят мгновенный характер, в определенном интервале температур профиль контура поглощения приобретает характерную прямоугольную форму, края которой спадают по мере удаления от максимума 7 ( to - to max ) ², что соответствует т = c onst.

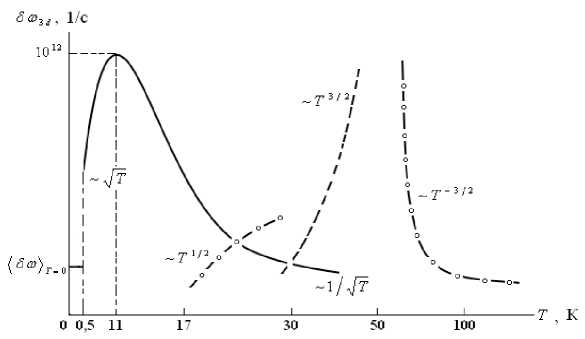
Рис. 1. Температурный ход полуширины линии поглощения ЦР при различных механизмах рассеяния. Сплошной кривой соответствует резонансное рассеяние на нейтральных примесях, штрихам и кружочкам, соответственно, рассеяние на тепловых колебаниях решетки и на ионах примеси. Окрестность нулевой температуры: 0 т 0,05 K приближенно описывается формулой (16) (см. прим. 2)

В квазидвумерном случае (q2D)

2d (k) =τ2d(k)

2 d 4-

П / п

2 ^tr d ( k ) =

2 d 4-

П / п

∗ m

k

π ²

k π ²

+ ln ²

^

∗ m

∗ m

2 d 2 n i п п

^

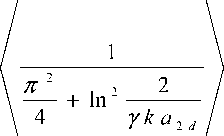
ε _{2 d}

γ ka _{2 d}

E

4 n2d П п 2   7     E exp (— E/kв T ) dE m * (к в T ) 2 0 п 2 + In2 ( y 2 m a r^ E Ь h 2) ^

d^f 2 П ² exp ( 4 U 0/ A U )

⁼             2     ∗ 2

γ m r ₀

4 nid П п 2   7 E exp (— E/k в T) dE m * (к в T)2 0 п 2 + ln2 (E /£ 2 d)

Здесь E - энергия движения в плоскости (р,^), n 2 d- поверхностная концентрация при месей, обычно n 2 d ~ 2 X1010 см 2. В формуле (8) под £2 d подразумевается эффективный вир- туальный и/или резонансный уровень в зависимости от знака расстройки потенциала. Интеграл в формуле (8) выражается через специальные функции [9, с. 588]:

δω 2 d ( k ) =

2 d 2

4 n i п п

∗

m

ε _{2 d}

kRT

V в 7

72 "

exp

ε2 d — k/T

V в 7

-

ν

′′

1 ε2 d kT

V ^в 7 J

,

µxdx где V (Ц) =          . Исследуем наиболее актуальный и интересный для ЦР случай - ушире-

0 γ( x + 1 )

ние при низких температурах. Для этого выделим в V ‘ ( ц ) асимптотическую экспоненту

∞

x - 2 µ ^x   d x

γ( x - 1 )

∞

= J

_µx - 1 dx Γ ( x )

+

2 x - 2 µ ^x   d x

^J Г ( x - 1 )

2 x-2 µx  d x exp ( µ) +

₀ γ( x - 1 )

( ц = £ _{2 d} (кк _в T ) ; Ц ^7 ), [10, с.117]. Тогда разность (с учетом множителя ц ²) в формуле (9)

2 (-µx) dx равна              , откуда 18 to т d (к )

0 Γ ( x - 1 )                    ^d

7 ---i------        /— . Оценку последнего инте- m∗      0 γ (x -1)

в уширение кривой классического циклотронного резонанса...

грала нетрудно найти, предварительно сводя его к виду

+ 1

- 1

(-A x ) dx Г( x )

(с учетом

+ 1

< А I

- 1

1 х , /     +1 х , А -1 /а

—х-^- а x d x <  А ■ A x dx = А ■ ~----

Г ( x )                ?1                 ln А

- A i , ( а » 1). ln А

В результате получаем низкотемпературную оценку уширения:

4 n ² d п ² h ⁽ £ 2 d / k в T ) 2 m *     Inl i T d T k B T l ’

( E 2 d » k в T ).

Целесообразно обсудить вопрос о пределах применимости полученной формулы.

Для квазидвумерного образца число свободных электронов в приповерхностном атомном слое по порядку величины равно ns - n^3 - (1015)    см-2 = 1010 см-2. Вырождение q2D пh 2 ns электронного газа наступает при T ---------, что соответствует температуре 0,3 K. Этим зна- m * kR в чением и определяется нижний предел применимости формулы (10). Из структуры формулы (10)

^ 10¹¹ с ¹ (рис. 2), объясня-

никак не следует ограничение на высоту пика: (8to)   - ---i--- max       m *

ется это тем, что асимптотический режим (10) формируется из числа электронов, энергия которых сильно зашкаливает от некоторого среднего значения. Хотя вероятность возникновения такого особого режима в ансамбле частиц, с максвелловским распределением по скоростям, весьма мала, но в принципе ею нельзя пренебречь. Она является следствием поглощения E -волны резонансными частицами, число которых при очень низких температурах пренебрежимо мало.

Очевидно, что в подобных ситуациях 8to >  ( 8 to ) max . Требуемое для наблюдения резонанса H -поле определяется из условия to _c - ( 8 to ) _max и составляет примерно 5 ■Ю³ Э.

В области высоких температур процедура вычислений реализуется по схеме:

^

A x

—

2 _dx

Г(x-1)

= а 2 exp ( А )

^

-1

A ^x dx

~

- 1

dx

Г( x)

[ 10 , с. 117 ] гс

Здесь Rg (x ) = —Ц, Г( x )

(

^

А 2 exp ( А )

^A ■ I ^A

- 1

x

dx -

Rg ‘ ( 0 ) ln ² A

A x a dx

Г( x)

1 - 1 / А ^- A ■ .

ln А

Rg ' ( 0 ) =

^^^^^^в

И x)

Г 2 ( x )

^

^^^^^^в

x —— 0

+1

^^^^^^в

( 1/ ^x ) ' = 1 .

( 1/ x ) 2

A x Г( x )

ln а

.

dx

v ] A <<

В результате для высокотемпературной асимптотики уширения получаем формулу

2 d ( k ^

4 n ^{2 d} h п ²

m * ^{ln ( k} в ^T / ^E 2 d ) ’

^{( E} 2 d ^ ^k B ^T )

Как видно, уширение в высокотемпературной области, слабо зависит от температуры. Физический смысл этого вывода очевиден: при высоких температурах (например, комнатных и выше) число быстрых электронов несравнимо больше чем медленных (резонирующих), число которых исчезающе мало, но опять же, из-за распределения Максвелла, они дают определенный вклад в уширение. Перефразируя, можно сказать так: особый режим (11) представляет собой «парциальный остаток» резонансного рассеяния в области высоких температур. Вероятность наблюдения такого режима всегда близка к нулю, так как он обычно быстро затушевывается другими механизмами уширения. Таким образом, в теоретическом отношении формула (11) представляет меньше интереса, чем (10). Для уточнения пределов оценки (10) необходимо оценить резонансный уровень.

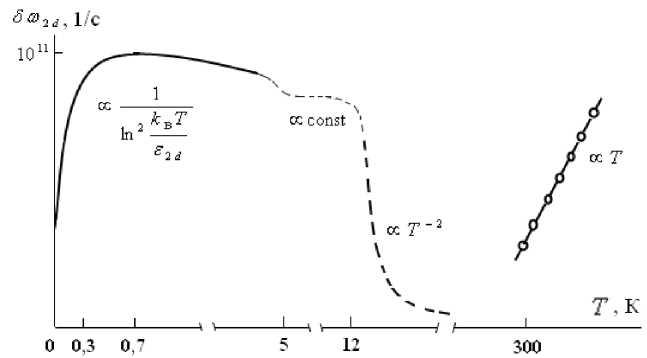
Рис. 2. Температурный ход полуширины линии поглощения ЦР при различных механизмах рассеяния. Сплошной линии соответствует резонансное рассеяние на нейтральных примесях [4], пунктирной линии - рассеяние на ионах примеси [11, с. 62]. Кружочки соответствуют рассеянию на приповерхностных акустических фононах. Температурный интервал 0,3т0,7 K - соответствует пределам выполнимости асимптотики (10). Приблизительно при температуре 5 K происходит плавная смена механизма рассеяния, в связи с включением рассеяния носителей на ионах примеси. Промежуток 0т0,3 K соответствует вырождению электронного газа. В пределах 5 т 12 K q2D -рассеяние носит столкновительный характер (плато): т 2_d = const ( q2D рассеяние учитывается в приближении

медленных частиц; при более высоких температурах ( T >  12 K) т 2_d

^ E ² и более строгое рассмотрение приво-

дит к зависимости ^ Й Ж2 _d

1 εkΒT i те------in-------- вместо T

T →∞

-

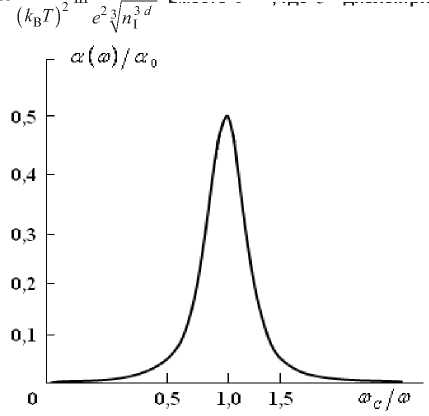
Рис. 3. 2D спектр поглощения. Окрестность максимума соответствует интервалу 5 т 12 K

² , где £ - диэлектрическая постоянная кристалла )

2. Оценка резонансного уровня в двумерной яме

Для оценки резонансного уровня воспользуемся формулой A U = ± 0,5 U ₀ [4], которая достаточно хорошо аппроксимирует зависимость расстройки потенциала от глубины мелкой при- меси. Этой формулы вполне достаточно чтобы оценить порядок £ _{2 d} . Полагая, что £ 3 _d порядка мэВ

(∆U )2

[2], из определения (3) т.е. из £_{3 d} = -------

4 U 0

16 °" , получаем U ₀ = 16 мэВ и A U = ± 8 мэВ.

Энергия резонансного s -состояния должна быть экспоненциально малой по сравнению с глубиной ямы [7, с. 201], тогда следует выбрать убывающую ветвь определения (8) из двух

2 Й²          I

ε _{2 d} = _{2 ∗ 2} exp - Y m r о    V

2          I

— I U ₀exp -

4 U 0 )

Муратов Т.Т. Вклад резонансного рассеяния носителей заряда в уширение кривой классического циклотронного резонанса...

Подставляя значения U 0 и A U в исходную формулу, находим что £ 2 d = 192 х e ⁸ - 0,06 мэВ, что соответствует области температур ^ 0,7 K. Данная оценка согласуется с нижним пределом асимптотики (10). Радиус потенциала мелкой водородоподобной примеси примерно равен r ₀ = = й/ 7 2 m* U ₀ - 1,5 х 10 ^{- 7} см. С учетом значений r ₀ и 2 U ₀/ 1 A U | определяем размеры волновых функции резонансных состояний: a ₂ d - 8,2 х 10 ⁶ см, a 3 d - 6 х 10 ⁷ см; которые фиксируют область локализации электронов проводимости. В условиях резонансного рассеяния a _{2 d} ^ X и a _{2 d} ^ X , где X ^ й^m * k _в T , откуда следуют значения T _{2 d} ^ 1 K и T 3 _d ^ 10 K.

Если методами молекулярно-лучевой или металлоорганической газофазной эпитаксии «уменьшить» диаметр d q2D- и/или 3D образца до такой степени что a_{N d} ^ d ( N = 2,3), то следует учитывать эффекты размерного квантования. Мы же предполагаем, что d ^ 10 ^{- 4} см [3].

• 3 . Расчет времени релаксации

  В квазидвумерной ситуации u _{2 d} =

  
  

  e \ ^T 2 d )

  —-—*—- и a _{2 d} « d , тогда m

  
  

  * m

  
  

  *

  m

  n V й

  
  

  ^

  ^х f

  
  
  
  

  4 n -^d й

  
  
  
  

  +

  
  

  ( п /2)² + ln² ( 2/ Y a 2 d Д п

  
  

  *  т~1

  mE

  
  

  E

  
  

  *

  m

  
  
  
  

  4 n 2 d Й ( k в T ) ^{2 X}

  
  

  +

  
  

  п²

  
  

  ln ²

  
  

  ( ..2    * T7 2 A

  Y m ^Ea 2 d

  
  

  V

  
  

  2 Й ²      ,

  
  
  
  

  \

  
  

  exp

  
  
  
  

  V

  
  

  E

  — k в T J

  
  

  E dE ^

  
  

  п ²

  
  

  (

  ^ln

  V

  
  
  
  

  k в T

  
  

  ^£ 2 d

  
  

  + 2 ( 1 - Y ) ln

  
  

  k в T

  
  

  +

  
  

  _-

  
  

  *

  m

  2 d

  4 n - й

  
  

  u 2 d ^{( T} )      .     2 с/ 2

  4 П 2d п ² й

  
  

  п ²

  
  

  L k в T

  ln-----

  V ^£ 2 d

  
  

  ^£ 2 d

  
  

  п ² - 6

  —

  6 )

  
  

  ^

  
  

  +

  
  

  ^{( 1 - Y} )

  
  

  +

  
  

  5 п ² + 6

  
  

  6 п ²

  
  

  .

  
  
  
  

  k_BT exp ^{( 1 -} у )

  ln² --------------------

  
  

  +

  
  

  ^£ 2 d

  
  

  5 п ² + 6

  
  

  , u 2 d ~

  
  

  , 2 ^k В ^T u ₀ ln ²

  ^£ 2 d

  
  

  .

  
  
  
  

Температурная зависимость подвижности (13) имеет суперслабо выраженный минимум при ^£а ^{exp [ - ( 1 -} Y ^{) ]}     2 ^£                e 5 п ² + 6

T _m ш =--------;---------- - -     , и тш = ,             ₂   = ^{5,3 х 10} 6 ^{см /В}^. ⁽¹⁴⁾

k _в              3 k _в            4 n 2 d й 6 п ²

Отметим, что значения подвижности ^ 10 ⁶ см²/В^с при T <  1 K вполне достижимы [11].

В отличие от объемного случая [2], минимум и _{2 d} не зависит от резонансного уровня а, следовательно, и от расстройки потенциала. С учетом значения £ _{2 d} - 0,06 мэВ из (14) находим что T min - 0,5 K (рис. 4). Минимум температуры локализован в пределах применимости (10) и вполне соответствует верхнему пределу выполнения асимптотики (10). Таким образом, как и ожидалось, особый режим уширения (10) имеет узкий интервал проявления 0,3^0,7 K (рис. 2).

Как видно, подвижность квазидвумерного невырожденного электронного газа в области 0,3 ^12 K , весьма слабо зависит от температуры, напротив, в окрестности абсолютного нуля имеет место резко выраженный рост (рис. 4). Графики на рис. 2 и 4 находятся во взаимно обратной связи между собой, что является следствием взаимно обратной пропорциональности между уширением и подвижностью. Это важная деталь позволяет заключить, что пику уширения и минимуму подвижности примерно соответствует температура порядка 0,5 K (рис. 2).

Рис. 4. Температурная зависимость 2D подвижности. Сплошной линией указана теоретическая зависимость (13). Штрихам соответствует рассеяние на ионах примеси, крестикам - рассеяние на акустических фононах [11, стр.62].

В окрестности 5 K происходит смена механизма рассеяния, который учитывается в приближении медленных частиц. В интервале 5 т 12 K (плато) преобладает рассеяние на ионах примеси, сечение которого в низкоэнергетическом пределе имеет корневую зависимость от энергии: с 2 d ^ 1/ Ее . При T >  12 K также преобладает рас-

сеяние на ионах примеси, однако, сечение рассеяния ^ E

Для определения температуры перехода следует рассмотреть двумерный аналог задачи о движении электрона в поле иона примеси. Как ив 3D случае смену механизма рассеяния будем τΙ        2m∗E учитывать в приближении медленных частиц. Известно что —2d- = y--------a [11, с.61], где т 3 d             h у - числовой множитель порядка единицы, a - ширина мелкой q2D ямы, a ~ r0.

∗

∗

γ a m

= const .

h 3 n 3 d

При E ^ 0 т 3 _d = -

π

m Ι

=---E ^{1 2} [6], в результате получим т 2 _d = —

3 d ₂                                              π

Смена механизма уширения предполагает: 3to2^s = 3to2od, E ^ kBT. Ясно, что при очень низ ких (10), также как и при очень высоких (11), температурах, «переход» не может быть реализо ван, но с учетом формулы 3щ2ds

4 n ^2dh n ²

m ^∗    ln² ( k _Β T ε _{2 d} )

[4] и 3to 2o d

n h 3 n I

----"----, находим γ a m ^∗

что T пер

ε 2 d

× exp k _Β

2 d

4 π a γ n _i

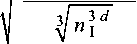
Экспоненциальный множитель не может быть слишком велик, поэтому, не нарушая общности, можно считать что Tпер « 5 K (рис. 4). Так как асимптотика (10) имеет верхним пределом значение 0,7 K, то остается предположить, что формула (11) работает в пределах 0,7 ^ 5 K. Тогда значение 0,7 K примерно соответствует пику уширения (3to) max (рис. 2).

Для инверсионных слоев [ ^ (10 ⁷ ^ 10 ⁶) см] формула (15) лучше соблюдается, чем для ква- 2 d          10     –2     3 d 12     –3

зидвумерных структур, причем ni = 2Х10 см , nz = 10 см , a = 1,5Х10   см. При этом размер двумерной волновой функции резонансного состояния на порядок превышает а и условие преобладания s -волны, хорошо соблюдается. Во всяком случае, температура перехода весьма чувствительна к концентрации мелкой донорной примеси.

По мере разогрева ( u _E ~ и _т ) время релаксации начинает зависеть от энергии частиц и столкновительное (аналогичное столкновению упругих шаров) рассеяние сменяется рассеянием электронов в кулоновском поле иона примеси. Из равенства средней тепловой энергии и потенциальной энергии можно оценит температуру смены специфики рассеяния. Оценка показывает, что смена происходит примерно при 12 K. Именно с этого значения кулоново поле ионов примеси начинает эффективно влиять на процесс рассеяния электронов (рис. 4).

Выводы

В объемных образцах при очень низких температурах вдали от области температур, соответствующих резонансному рассеянию электронов (левое крыло) кривая поглощения резонансно уширяется ^ Тт , а при «высоких температурах» (правое крыло) « 1/ Тт . Асимптотика (6) эффективно работает в пределах 0,5 ^10 K (в указанных пределах все ещё не нарушается квазиклассичность: X <  ( n 3 d ) - ^{1 3}), при более низких 0,05^0,5 K температурах требуется учет частичного вырождения электронного газа. Асимптотики (7) и (11) по сути, являются парциальным остатком резонансного рассеяния в области «высоких температур», на фоне других доминирующих механизмов рассеяния: (7 a ), (7 б) .

Значение возможного резонансного уровня в q2D образцах примерно составляет 0,06 мэВ.

Пределы применимости асимптотики (10) 0,3^0,7 K. В интервале 5^12 K двумерное рассеяние электронов на ионах примеси, носит в основном, столкновительный характер (контур Лоренца, жесткая решетка, плато на рис. 2 и 4).

Примечание 1

Эксперименты показывают, что возможный резонансный уровень в ковалентных полупроводниках порядка мэВ [2], что соответствует нескольким кельвинам. При этих условиях длина волны электрона гораздо меньше его длины свободного пробега: X^fc ^ 1 / n ^{3 d} ^ 10 - ⁴ см [3]. Классический предел ЦР предполагает выполнение условия X <  fc _н , а для наблюдения ЦР необходим по крайней мере один оборот, так что fc _н ^ fc и энергия электрического поля расходуется на расширение циклотронной орбиты. Число квантовых состояний в кристаллах порядка 10²² В типичных полупроводниках концентрация носителей заряда колеблется в пределах 10¹⁰ ^ 10¹⁸ см^-3, и соответственно чему энергия электрона ^ k _в T ( X < ( n ^ ^d ) , n 3 ^d <  10¹⁵ см^-3).

В дальнейшем, для упрощения различных оценок мы полагаем m * = m e = 9,1 х 10 - ²⁸ г и используем систему СГС, как предпочтительную.

Примечание 2

Границы применимости асимптотики (6) однозначно определяются температурным ходом химпотенциала в области примесной проводимости: при T = 0 K уровень химпотенциала проходит посередине между дном E C и примесными уровнями, а затем начинает подниматься. С учетом того что A E D ^ 0,01 эВ, а n _D велико, то уровень химпотенциала может приблизиться к дну зоны проводимости и даже пересечь его, так что неравенство f ₀ « 1 нарушится и все прежние выводы, основанные на нем, будут по крайней мере не точны. Учет частичного вырождения требует больших трудоемких вычислений, однако можно попытаться оценит нижний температур-

_∗      32

ный предел асимптотики (6): N _с = 2 •

• ^{2    п} m k в ^т

  ; концентрация электронов в зоне прово

  
  

. ( 2 п й)2 , димости (ne3d < 2•Ю15 см 3; перебросы из V-зоны в C-зону за счет межзонной подсветки; при концентрациях n3 d > 2 х1015 см-3 следует учитывать интерференцию от отдельных D- -центров) сравнивается с эффективной плотностью состояний в последней при температуре 0,5 K. Примерно при 0,05 K уровень химпотенциала пересекает EC и газ становится полностью вырожденным. Для оценки верхнего температурного предела следует учесть смену механизмов рассеяния. Ясно, что при более высоких температурах (от возможного верхнего предела) сечение рассеяния не зависит от энергии рассеиваемых частиц: оI = (n3 d )-23 (приближение медленных частиц), где оj - эффективный поперечник иона примеси, n 3 d - концентрация ионов примеси. Смена механизма рассеяния предполагает fcres = fc I . Оценка показывает что fcres = 4х10 - 4 см [3]. Примерно то же значение длины свободного пробега достигается при концентрации ионов

• 3    d 1 а 12    —3                            3 d / 3 d      ^AE d / ^k в T 1 a ^_ 3               ^rp л ту тт

n i -10 см , с учетом того что ni lni = e D/ в - 10   , получим Tnep - 16,7 K. Пи ку уширения примерно соответствует температура Tmax ^ е 3 d / кв - 11,6 K (определение Tmax на основе точной формулы (3) требует решения сложного трансцендентного уравнения), именно при этой температуре нарушается аппроксимация е0 »1.

Таким образом, в качестве верхнего предела асимптотики (6) целесообразно взять 10 K.

В окрестности T = 0 K lim f 0 -1, (EF — E > EC). Из-за сильного перекрытия примесных волновых функции примесные уровни вырождаются в примесную полосу с шириной Г (0 ) при нулевой температуре. Соответствующий расчет на основе формулы Брейта-Вигнера приводит в этом случае к приближенной формуле (формально это соответствует случаю U = 0)

дм 3 _d ( к , T = 0 )^ -

• ⁵ * ⁿ d \ ² E res Г ( 0 ) ~ Г ( 0 ) , ( T е 0 + 0,05 K).     (16)

А ( m • ) ^3,2 E^

Здесь E F ( 0 ) = E C ⁺ E D , E _res — резонансный уровень, E D — энергия связи D -уровня.

При отсутствии перекрытия (перехода Мотта) ( r < у ³ n i ^d , где r - радиус локализации свободного электрона); ^ щ ₃ d ( к , T = 0 )^ 1/ е _{3 d} ^ | A U |”1 , ( T е 0 ^ 0,05 K) .

Математическое дополнение

В промежутке между двумя асимптотиками (6) и (7) можно выделить переходную область:

— Ei ( — е ₀ ) = J ex^ ^е 0

I exp ( — е 0 ) J е 0 , е 3 _d >  5 • к в T dt - <

^— у ⁺ In ( 1/ ^е 0 ) , ^е 3 d <  k в ^T /5

Данная аппроксимация удобна для общего анализа профиля уширения в окрестности пика когда аппроксиманты (10) и (11) не вполне приемлемы (в пределах нулевой зоны Ландау). Подставляя exp(—е0)/е0 в L(е0) = 1 — е0 ехр(е0)[—Ei(—е0)] автоматически получим нуль, со ответственно чему dto 3d 0 ^ 0. Разумеется, полученный результат следует рассматривать как некоторую о -символику более общих теоретических формул [8].