Влияние атмосферной турбулентности на спектральный состав радиосигнала

Различие атмосферной рефракции для различных длин волн в спектре радиосигнала определяет влияние турбулентности на спектр радиосигнала. Основной вклад в флуктуации амплитуд радиоволн под действием турбулентных пульсаций, составляющих спектр радиосигнала, вносят верхняя тропосфера и нижняя стратосфера.

Влияние турбулентности приводит, во-первых, к изменению спектральной флуктуации интенсивности радиосигнала, а во-вторых, к изменению спектра радиосигнала за счет сдвига длин волн в спектре. Эти два процесса связаны между собой.

Рассмотрим средний квадрат флуктуаций интегральной (по спектру) интенсивности радиосигнала за счет турбулентности атмосферы:

^ 2 ^ 2

= 1111 '(к) I '(к')) d1 dк'’ (1) к1 к1

J J '2) =Hi -( I ) d I

где I'(к) - флуктуации спектральной плотности интенсивности, принимаемой антенной, радио- волны; 11 и ^2 - границы спектра радиоволны, угловые скобки означают процесс осреднения.

Будем считать, что в результате воздействия турбулентности на радиосигнал произошел сдвиг отдельной длины волны в спектре с величины 1 до к' .

Спектральную зависимость плотности интенсивности радиоволны в случае малых флуктуаций, рис. 1, примем в виде

• ¹    ( ^к ) = ¹ о (^к) e ^2x1 « ¹ о ( ^к )( 1 + ² х к ) , (2) где I о ( к ) - предполагаемая спектральная плотность интенсивности радиоволны на границе тропосферы и стратосферы; / к ( к ) — спектральные флуктуации амплитуды эйконала радиосигнала за счет турбулентности [1]. Коэффициент 2 использован, т. к. интенсивность радиосигнала (или модуль вектора Пойнтинга) пропорциональна квадрату напряженностей электрического и магнитного полей в электромагнитной волне.

Следовательно, спектральные флуктуации интенсивности радиосигнала за счет турбулентности атмосферы относительно границы стратосферы и тропосферы имеют вид

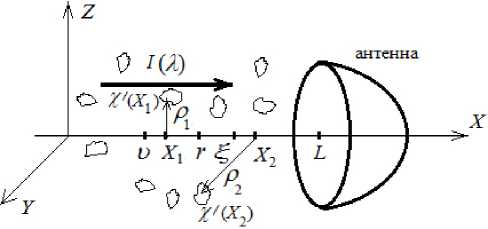
Рис. 1. К анализу пространственной двухточечной корреляционной функции флуктуаций эйконала радиосигнала в турбулентной атмосфере

Fig. 1. On the analysis of the spatial two-point correlation function of the eikonal fluctuations of a radio signal in a turbulent atmosphere

I '(^) = I W- I 0 W« ² I 0 Wx k .                  (3)

Таким образом, формулу (1) для среднего квадрата флуктуаций интенсивности интегрального радиосигнала можно записать как λ ₂ λ ₂

J ′ ² = 4 ∫∫ I ₀ ( λ ) I ₀ ( λ′ ) χ′_λχ′_λ ′ d λ d λ′ =              (4)

λ 1 λ 1 λ ₂ λ ₂

= 4 J J 1 0 ( X ) 1 0 ( X‘ ) B _xx ( X , X’ ) d X d X’ , λ ₁ λ ₁

где B _xx ( X , X‘ ) = ^x X ( X ) x X' ( X’ )) — двухволновое корреляционное соотношение амплитудных пульсаций эйконалов в спектре радиосигнала за счет турбулентности атмосферы [2].

Если имеется пространственное поле пульсаций эйконала радиосигнала за счет турбулентности x‘ ( X ) , рис. 1, то Фурье-интеграл пространственной двухточечной корреляционной функции B _χχ = χ′ ( X ₁ ) χ′ ( X ₂ ) имеет вид [1]:

B xz = J e - i ^k'^P F z ( ^k ‘ ^{, X} I ^{, X} 2 ) d ^k ‘ ,                       ⁽⁵⁾

где k ′ – волновой вектор флуктуаций эйконала электромагнитной волны за счет турбулентности; p = ( p + p )/2, p и P 2 — радиусы векторы с началом в точках X ₁ и X ₂ на оси Х в плоскостях ( Y , Z ) , модули которых вычисляются по формулам р = 7 Y ² + Z ² , рис. 1; F _XX ( k ‘ , X 1 , X ₂ ) — двух— точечный Фурье-спектр флуктуаций эйконала радиосигнала.

Решение дифференциального уравнения для флуктуаций эйконала амплитуды электромагнитной волны [1] записывается как

^{X 1 X 2}    k ′ ² ( X -υ )

F U ^k‘ ^{, X} 1 ^{, X} 2 Н B z ² k ² J J ^si"     a ^x (6

^{X sin} k ⁽ ₂ 2 ^ F nn ( ^k ‘ , ^U’^ ) d ^U d ^

где ζ – волновое число турбулентных пульсаций; k – волновое число радиосигнала; υ и ξ – координаты на оси Х источников воздействия турбулентности на электромагнитную волну, рис. 1; F_nn ( k ‘ , и , ^ ) — двухточечный Фурье-спектр флуктуаций показателя преломления за счет турбулентности; µ и B = 4 – постоянные величины.

В формуле (6) для сохранения размерностей физических величин уменьшена степенная зависимость спектральной функции F _xx ( k ‘ , X 1 , X 2 ) от волнового числа турбулентных пульсаций до Z 2 . Как будет показано в дальнейшем, это не влияет на конечный результат анализа.

На фронте волны при X 1 = X 2 = L, рис. 1, формула (6) для Фурье-спектра преобразуется в

^LL   k ′ ² ( L -υ )

^F xx ( ^kW k ² П sin  2 k   x             (7)

k ′ ² ( L -ξ )

^{x sin}---^--- F nn ( ^k ‘, ^u , ^ ) d ^u d ^

2k где обозначено F (k‘, L, L) = F (k‘). χχ χχ

Фактически рассматривается единая точка наблюдения на оси Х воздействия турбулентных пульсаций на электромагнитную волну.

Несложная модификация решения дифференциального уравнения для флуктуаций эйконала амплитуды электромагнитной волны [1] для двухволновой корреляционной функции B xx ( X , X‘ ) = =χ′_λ ( λ ) χ′_λ′ ( λ′ ) показывает, что Фурье спектр F xx ( k ‘ , X , X‘ ) должен быть записан в форме

₂ ^LL k ′ ² ( L -υ )

F _xx ( k ‘ , X , X‘ ) = ^Z 2 k 1 k ₂ II sin---^------x

2 k 00         ¹

x sin

k ′ ² ( L -ξ )

2 k ₂ ^Fnn

( k ‘ , u , ^ ) d и d ^ ,

где k 1 = 2 п / X и k 2 = 2 n / X‘ - волновые числа длин волн радиосигнала (исходной и сдвинутой за счет влияния турбулентности) на координатах воздействия турбулентности на радиосигнал и и ^ .

При X1= X2= L можно рассматривать единый источник воздействия турбулентности на радиосигнал в точке координаты Х распростра- нения радиоволны, т. е. ввести новую переменную r = (u + Ш 2.

Следовательно, формулу (8) можно записать в виде

,        .      ₂ LL k ^,2 ( l - r )

F _n( k ‘ , X , X' ) = ^² k i k 2 JJ sin —2 k x            (9)

00          ¹

= sin

x sin

^k '2 ( ^L - r ) F

2k ₂      ⁿⁿ

( k ‘ , r ) d и d ^ .

( k '² ( L - r ) )

x sin

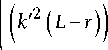
k 2 + k i ₄ ^{2 k} i ^k 2

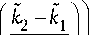
ч ^{2 k} i ^k 2 J

Кроме того, необходимо осуществить замену дифференциального элемента в двойном интегра ле d и d 1 по формуле [3]. Представим 1 = L ф / 2 n , где 1 меняется в пределах (0, L ) при изменении ф - угловой переменной в пределах (0,2 п ). Следовательно, и = 2 r - L ф / 2 п . С помощью якобиана J дифференциальный элемент d и d 1 преобразуется:

Учитывая k2 + k1    1     k2 - k1

--Z“Z3-- = и --Z“Z3-- =,

2k1k2    2k1     2k1k22

получаем тождество (12).

Подставив тождество (12) в подынтегральное выражение (11), запишем:

ди

ди

d и d 1 = | j|drd ф =

L 2 п L 2 п

д r 5^

д r

дф 31 дф

drd ф =

L

F _xx ( k ‘ , X , X' ) = 2 ц1 2 k ₁ k ₂ L J

k '² ( L - r ) sin--------- x

2 k ₁

drd ф = 2 — drd ф . 2 п

k '² ( L - r ) x sin---------

2 k ₂

f L = 2^2 k i k ₂ L J

F nn ( ^k ' > ^r ) ^dr =

2 k '2 ( L - r ) sin²---i-----X

Таким образом, формула (9) сводится к одиночному интегралу по независимой переменной r :

-

L 2 n

F xx⁽ k ’ ^X , ^X ) = ² ^^{z k} 1 ^k 2 2 n J J

k '² ( L - r ) sin--------- x

2 k ₁

L. 2 k '2 ( L - r ) sin --- \z----

^J 0       ² ^

2 k ₁

F nn ( k , ^r ) ^{dr -}

F nn ( ^k , ^r ) ^dr .

J

k '² ( L - r ) x sin---------

2 k ₂

L = 2 ц£ ² k 1 k ₂ L J

F nn ( ^k , ^r ) ^drd ф =

k '² ( L - r ) sin---------x

2 k ₁

k '² ( L - r )      ,     .

^{x sin}-------- F nn ( k ‘ , r ) ^dr .

2 k ₂

Для вычисления интеграла (11) докажем три-

гонометрическое тождество в подынтегральном

выражении:

k '² ( L - r )     k '² ( L - r )

s i n------------ s i n------------

2 k ₁           2 k ₂

• - sin2 ^{k ,2 ( L} r ) sin2 ^{k ,2 ( L} r )

• = sin -----z--sin -----z----,

2 k ₁              2 k ₂

где k i = 2 п / X i , а величины X i = ( X + X‘ )/ 2, а X 2 = = ( X-X‘ )/ 2 - полусмещение длины волны за счет влияния турбулентности.

Для доказательства (12) преобразуем по извест-

ным тригонометрическим тождествам правую

часть формулы (12):

₂ k '² ( L - r )       ₂ k '² ( L - r )

sin²---^---- - sin²---\z----

2 k ₁              2 k ₂

Проводя аналогичные преобразования для Фурье-спектра одноволновой корреляционной функции (7) с использованием переменной r = ( и +1 ) / 2 и формулы для произведения подынтегральных дифференциалов, аналогично (10) получаем интеграл от одной независимой переменной r :

, _{х 2 2} LL     k '² ( L -и )

Fxx(kx) = ^kJJsin   2k---X(15)

k '2 (L-1)     ,.

^{x sin}           F nn ( ^k ' > ^u , Ю ^{d u d} ^ =

2 k

• 2    2 p 2 k,2 (L - r)      ..

• =    2^ 2 k ² L J sin ²     2 _k ’ F nn ( k ‘ , r ) dr .

где волновое число k = 2 п / X .

Таким образом, формула (14) связи между двухволновым Фурье-спектром и одноволновыми спектрами принимает вид

F xx ( ^A'h >  F xx ( k '^X 1 ) -> F xx ( k ^X 2 ) = (16) k ₁ k ₂

• =    xX F ^{xx ( k} ‘^{X 1 )-}xx⁷ F ^{xx ( k X 2} ) .

В (16) степенная зависимость Z 2 сокращается в правой и левой частях равенства, поэтому этот со-

множитель, как отмечалось ранее, не участвует в дальнейшем анализе.

Имея соотношения между спектрами (16), можно получить связь между соответствующими корреляционными функциями (5):

Bxx (k', X, X) = (4 (k', X)4, (k', X')} =

• - j e i ^k ' ^₽ F _n(^k’ X 1 • X X 2 ^X ) d ^k ' =

( 2                12

• - je-ik ₽ ^' 'kX1 )4FkX2) dk' = \7

• - ^ Bxd ^k '^X 1 )-> B U ^k'^X 2 ) •

находим:

B nn ( ^{X , X}' ) = 4 e ( 1 -s ² ) z ³ •

Предположим в формуле (4), что величины I ₀ ( X ) и I ₀ ( X ) на границе тропосферы и стратосферы приблизительно постоянные. Тогда формулу (4), используя B nn = ц B xx , можно переписать так:

I 0 ( ^X ) I 0 ( ^X' )

X ₂ X ₂

= ⁴ П B u^{x , x}) d ^x d ^x '=

X 1 X 1

Координаты X 1 = X 2 = L как аргументы спектров в процессе вывода опускаем.

Используя связь между корреляционной функцией флуктуаций амплитуды эйконала радиосигнала за счет турбулентности и корреляционной функцией флуктуаций показателя преломления атмосферы за счет турбулентности B nn = ц B xx [1], где ц - постоянный масштабный коэффициент

x ₂ X ₂

-⁴ [ [ B nn ( X , X' ) d X d X' ,

ц

X 1 X 1

Используя формулу (21), а также учитывая X 1 -- ( X + X' ) / 2, запишем (22) в виде

1 02 ( X 1 )

4 ^X 2 ^X 2

-ц ez ³ // ( 1 -s ² )

X 1 X 1

d X d X' =

пропорциональности, находим:

=ц^{eZ 3} ( ^X 2

-

^{4 X} 2 ^X 2

X 1 ) 2 - ³ eZ ³ j J s ² d X d X' . ^ц

B_nn (k ' , X , X') - 1BB_m (k 'Aj- B_nn (k ' ,X₂ )• (18)

ПП              XX ' ПП 1 XX ' ПП 2

Найдем второе слагаемое в (23). Для пользуем переменные X 1 = (X + X ')/ 2

этого ис- и X2 =

В [2; 4; 5] была вычислена зависимость для одноволновой корреляционной функции от волнового числа турбулентности Z и радиуса p с началом координат на оси Х :

= ( X-X ' )/ 2. Применяя якобиан, преобразуем произведение дифференциалов под знаком двойного интеграла (23):

B nn ( р ) = Р

4 z ³

10 А

\

-

—Z ³ 40

Р

)

d X d X '

= J|d X 1 d X 2 =

dX dX 1 ax' dX 1

dX dX 2 dX' ^dX 2

d X 1 d X 2 =

где в - постоянный коэффициент.

Нас интересует функциональная зависимость

спектра радиосигнала на оси Х от атмосферной турбулентности, поэтому положим р = 0. Вследствие этого, полагая B nn ( р ) = B nn ( ^k ' • ^X 1 ) « B nn ( ^k ' • ^X 2 ) • формулу (18) преобразуем как

Q X ² -X ^{2 4}

B nn ( X ^X ' ) = 7 в        Z ³ •                         (20)

4 XX

Вводя обозначение

X X-X s = ^2- =-----

X 1 X + X'

– относительное спектральное смещение длины волны радиосигнала за счет турбулентности, а, также полагая в процессе преобразований приближенно X ®X' , так что

^* X

1 =

[ X + X ' А ²

I 2 J

® X ² ®XX' ,

^*     ^*

^*

^*

d X 1 d X 2 = 8 d X 1 d X 2 •

Следовательно, учитывая

s = X 2 / X 1 , найдем:

x ₂ x ₂                   ;

j j s ² d X d X ' = 8

X 1 X 1                     :

\ ^{2 X},²1 ²

. j j    d X , d X 2 =

X 1 X 1 ^X 1

-

8 ^{X 3}

3 X 1

^X 2

^X 1

-

8 s ³ X 2

^X 2

^X 1

-

3 ^s 3 ( ^X 2 ^-X 1 ) •

Таким образом, формула (23) преобразуется следующим образом:

J ^{2            4}<

K ( Z , s ) =------— ----- = -eZ ³ I 1 + 8 s ³

( X 2 -X 1 ) ² 1 2 ( X 1 ) ^ц I ³

где K ( Z , s ) - относительный безразмерный параметр, учитывающий влияние атмосферной турбулентности на средний квадрат флуктуаций

интегральной (по спектру) интенсивности радиосигнала. Влияние турбулентности на спектр радиосигнала характеризуется относительным спектральным смещением длины волны радиосигнала s = ( X-X' )/( X + X' ).

На рис. 2 показан график зависимости по формуле (25), построенный, как и в [2], при условии P = ц . Размерность отношения [ p / ц ] = м ^4/3 .

Как следует из рис. 2, параметр среднего квадрата флуктуаций интегральной интенсивности радиосигнала K ( Z , б ) растет с увеличением волнового числа турбулентных пульсаций Z . При этом, чем больше относительное смещение длины волны радиосигнала б, тем круче рост K ( Z , б ) . При малых б< 0,2 величина флуктуаций интегральной интенсивности радиосигнала K ( Z , б ) практически не зависит от смещения спектральных длин волн радиосигнала б за счет турбулентности.

С практической точки зрения это указывает на то, что турбулентность мало искажает спектральную информационную сущность распространяющегося радиосигнала в различных диапазонах длин волн.

Заключение

В работе проведено исследование влияния турбулентности атмосферы на интегральную и спектральную интенсивность радиосигнала.

Найдена связь между двухволновой корреляционной функцией амплитудных пульсаций эйконалов в спектре радиосигнала за счет турбулентности атмосферы и пространственной двухточечной корреляционной функцией.

На основе решения дифференциального уравнения для флуктуаций эйконала амплитуды электромагнитной волны найдена связь между двухволновым Фурье-спектром и одноволновыми спектрами. При этом использован единый источник воздействия турбулентности на радиосигнал в точке координаты Х распространения радио-

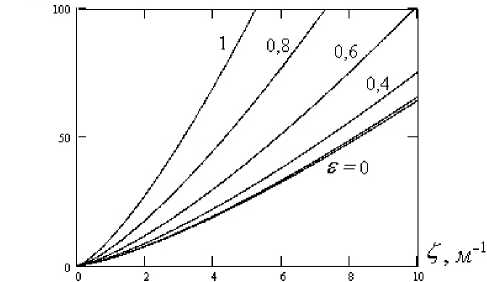
Рис. 2. Зависимость относительного безразмерного среднего квадрата флуктуаций интегральной интенсивности радиосигнала от волнового числа турбулентных пульсаций атмосферы Z при различных смещениях спектральных длин волн радиосигнала б

Fig. 2. Dependence of the relative dimensionless mean square of fluctuations of the integral intensity of a radio signal on the wave number of turbulent pulsations of the atmosphere Z for different shifts of the spectral wavelengths of the radio signal б волны путем введения новой переменной, равной среднему значению координат воздействия турбулентности. Для нахождения двойного интеграла одна из координат воздействия преобразована в угловую переменную.

При использовании ранее найденной зависимости одноволновой корреляционной функции от волнового числа турбулентности Z получена формула связи относительного безразмерного параметра, учитывающего влияние атмосферной турбулентности на средний квадрат флуктуаций интегральной (по спектру) интенсивности радиосигнала. Показано, что влияние турбулентности на спектр радиосигнала характеризуется кубом относительного смещения спектральной длины волны в 3 радиосигнале б .

Установлено, что турбулентность мало искажает спектральную информационную сущность распространяющегося радиосигнала в различных диапазонах длин волн.