Влияние атомной когерентности на перепутывание атомов с двухфотонными переходами с учетом динамического штарковского сдвига

Одной из фундаментальных проблем современной квантовой информатики является рара-ботка механизмов контроля и управления перепутыванием кубитов [1]. В последнее время в ряде работ показана возможность управления перепутыванием кубитов, взаимодействующих с внешними полями, за счет использования динамического штарковского сдвига. Гош и др. впервые показали, что штарковский сдвиг может быть использован для значительного увеличения степени атомного перепутывания атомов с двухфотонными переходами в резонаторе в сравнении с тем, что имеем место в резонансном приближении [2]. Абдель-Ати и Мойа-Гесса установили, что штарковский сдвиг может приводить к эффекту мгновенной смерти перепутывания и долгоживущему перепутыванию двух ионов в магнитной ловушке, приготовленных в сепарабельном состоянии или смешанном состоянии [3]. В работах [4–6] на примере двойной и обычной двухфотонной модели Тависа-Камминг-са показано, что в присутствии штарковского сдига степень атомного перепутывания может существенно возрастать при наличии штарков-ского сдвига в случае начального перепутанного состояния атомов. В работе [7] установлено, что для двух атомов с двухфотонными переходами, взаимодействующие каждый со своим полем в резонаторе штарковский сдвиг позволяет управлять степенью перепутывания и осущест- влять контроль за эффектом мгновенной смерти перепутывания. Наконец, в работе [8] доказана возможность увеличения степени перепутывания трех атомов, взаимодействующих с тремя различными резонаторами, за счет включния штарковского сдвига. Результаты указанных работ указывают на то, что штарковский сдвиг может быть эффективным механизмом усиления степени перепутывания атомов и ионов с двухфотонными переходами. Заметим, что для атомов и ионов, взаимодействующих с электромагнитными полями в резонаторах посредством двухфотонных переходов, штарковский сдвиг уровней можно легко контролировать, изменяя величину расстройки между удвоенной частотой резонаторной моды и частотой атомного перехода.

В настоящей работе мы обобщим результаты работы [5] по исследованию влияния штарков-ского сдвига на атомное перепутывание в двухатомных системах с двухфотонными переходами на случай неперепутанных когерентных начальных состояний атомов. Основное внимание будет уделено исследованию влияния атомной когерентности на атомное перепутывание при наличии штарковского сдвига. Для количественной оценки степени атом-атомного перепутывания будем использовать вместо согласованности [9], которая рассчитывалась в работе [5], параметр Переса-Хородецких [10; 11], так как положи

тельность данного параметра для системы двух кубитов является необходимым и достаточным условием их перепутанности. Заметим, что другой механизм контроля перепутывания кубитов, связанный с диполь-дипольным взаимодействием рассматривался нами в работах [12–19].

Будем исследовать систему, состоящую из двух атомов, взаимодействующих с квантовым электромагнитным полем в идеальном резонаторе посредством вырожденных двухфотонных переходов. Для того, чтобы получить эффективный двухфотонный гамильтониан, рассмотрим два идентичных трехуровневых атома, обладающих тремя энергетическими уровнями | +〉 , | i 〉 и | -〉 , где | +〉 – возбужденое, | i 〉 – промежуточное | -〉 – основное состояние обоих атомов. Предположим,что каскад атомных переходов | +〉 → | i 〉 → | -〉 находится в резонансе с удвоенной частотой резонаторной моды, т. е. имеет место соотношение ω ₀ = 2 ω , где ω ₀ – частота атомного перехода между возбужденным и основным состояниями атома, а ω – частота резонаторной моды. Пусть при этом частоты переходов между возбужденным и промежуточным и промежуточным и основным состояниями атома сильно отстроены от частоты резонаторной моды. В этом случае мы можем адиабатически исключить промежуточный уровень в каждом атоме и получить эффективную модель двух двухуровневых атомов с вырожденными двухфотонными переходами [20–22]. Учитывая также штарковский сдвиг энергетических уровней [23], мы можем окончательно записать эффективный гамильтониан двух двухуровневых атомов, взаимодействующих с квантовым электромагнитным полем в идеальном резонаторе посредством вырожденных двухфотонных переходов 2

Hi = Й g ^ (.a ^{l 2} c - + c⁺ a ²) + i =1 2

+ ^ Й a ⁺ a ^{( e} 2 ^c+c - ^+e 2 ^c - ^{c +} ), i =1

где a ⁺ и a – операторы рождения и уничтожения фотонов резонаторной моды; σ _i ⁺ и σ _i ^- – повышающий и понижающий операторы в i -ом двухуровневом атоме ( i = 1, 2); β ₂ и β ₁ – параметры, описывающие зависящие от интенсивности штарковские сдвиги энергетических уровней и g – эффективная константа двухфотонного атом-полевого взаимодействия.

Предположим, что каждый из атомов первоначально приготовлен в в чистом когерентном состоянии, но сами атомы не перепутаны, т. е.

| Ψ A 1 (0) 〉 =cos θ 1 | +〉 + e^{i ϕ 1}sin θ 1 | -〉 ,

|ΨA2(0)〉 =cosθ2|+〉 + eiϕ2sinθ2|-〉, где θ1 и θ2 – амплитуды поляризованных атомов; ϕ1 и ϕ2 – относительные фазы возбужденного и основного состояний каждого из атомов (в дальнейшем мы будем также использовать разность фаз ∆ϕ = ϕ2- ϕ1), а поле приготовлено в состоянии с определенным числом фотонов |n〉. Тогда чистое начальное состояние для полной системы «атомы+поле» есть

| Ψ (0) 〉 =| Ψ A 1 (0) 〉 | Ψ A 2 (0) 〉 | n 〉 .                     (2)

Динамика атомного перепутывания существенно зависит от начального состояния резонатора. Поэтому рассмотрим отдельно начальные состояния с n = 0,1, 2.

Пусть в начальный момент времени в резонаторе отсутствуют фотоны, т. е. n = 0. Тогда полная временная функция рассматриваемой модели с гамильтонианом (1) и начальным условием (2) при n = 0 может быть написана как

| Ψ ( t ) 〉 = X ₁( t )| + , + ;0 〉+ X ₂( t )| + , - ;0 〉+

+ X ₃( t ) | - , + ;0 〉+ X ₄( t ) | - , - ;0 〉+

+ X ₅( t ) | + , - ;2 〉+ X ₆( t ) | - , + ;2 〉+

+ X ₇( t )| - , - ;2 〉+ X ₈( t )| - , - ;4 〉 .

Используя временное уравнение Шредингера для волновой функции (3), мы можем получить явные уравнения движения для коэффициентов X i ( t ):

iX 1 = V2g (X 5 + X 6), iX 2 = iX 3 = V2gX 7, iX 4 = 0, iX 5 = V2gX 1 + 12ggX 8 + 2в2 X 5 + 2в1 X 5, iX 6 = V2gX 1 + 22ggX 8) + 2в1 X 6 + 2вд X 6, iX^ 7 = V2g (X 2 + X 3) + 4в1 X 7,

iX : 8 = 712 g ( X 5 + X 6 ) + 8 в 1 X 8 .

Поскольку точное решение уравнений (4) чрезвычайно громоздко, мы будем использовать в дальнейшем численные решения указанных уравнений. Информация о перепутанности двух атомов содержится в редуцированной атомной матрице плотности ρ _A ( t ), которая для случая начальных чистых состояний атома и поля может быть получена следующим образом

ρ A ( t ) = Tr F | Ψ ( t ) 〉〈Ψ ( t ) |.

Здесь операция Tr_F представляет собой усреднение по переменным поля. Для двухкубитной

системы редуцированная атомная матрица плотности р a ( t ) в двухатомном базисе | + , +) , | + , -) , | — , +) , I — , - имеет вид

	р 11 р 12 р 13   р 14Л
	р 21 р 22 р 23 р 24
р =		.                               (5)
	р 31 р 32 р 33 р 34
	ч р 41 р 42 р 34 р 44 7

Для определения степени атом-атомного пе-

репутывания будем использовать параметр Переса – Хородецких, который определяется как s = -2^ц -,                                (6)

i

где ц j — отрицательные собственные значения транспонированной по переменным одного кубита атомной матрицы плотности р A , которая для двухкубитной системы с атомной матрицей плотности (2) может быть представлена как

г^р 11 ^р 12 ^р 31 ^р 32 ^

T

Р A =

^р 21

^р 13

^р 22 ^р 41 ^р 42

^р 14 ^р 33 ^р 34

\^р 23 ^р 24 ^р 43 ^р 44 J

Отсутствие у частично транспонированной по переменным одного кубита атомной матрицы плотности (4) отрицательных собственных значений означает, что атомы в любой момент вре-

мени остаются неперепутанными, в этом случае полагают s = 0. Для случая s > 0 атомы находят-

ся в перепутанном состоянии. Для максимально

перепутанного состояния s = 1.

Для системы, описываемой волновой функций (3) в двухатомном базисе частично транспониро-

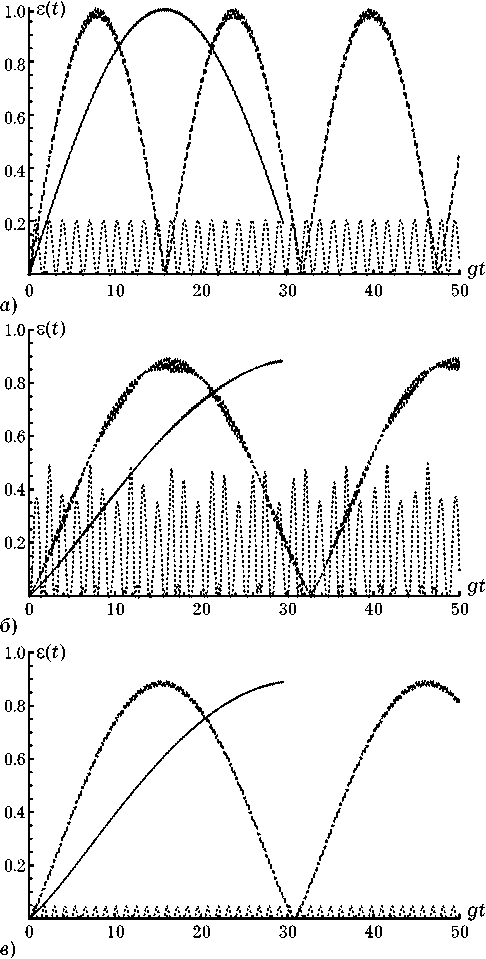
Рис. 1. Временная зависимость параметра перепутывания для начального состояния вида (2) и параметров штарковского сдвига P i = Р 2 = 0 (точечные линии), P i = Р 2 = 5 g (штриховые линии) и P i = Р 2 = 10 g (сплошные линии). Амплитуды поляризованных атомов 0 1 = п /2, О 2 = 0 ( а ), 0 1 = п /4, О 2 = п /4 ( б ) и 0 1 = п /4, О 2 = -п /4 ( в ). Разность фаз Дф = 0

ванная по переменным одного кубита атомная T матрица рA (t) может быть выражена как

	Г	I X 1 I2	X 1 X 2
T		X 2 X *	I X 2 I2 + I X 5 I2
Р A =
		X 1 X з	X 1 X 4
		*             з
	( X 2 X 3 + X 5 X 6		X 2 X 3 + X 5 X *
	*		____*    ____*       \
X 3 X 1			X 3 X 2 + X 6 X 5
	*		*
X 4 X 1			X 4 X 2 + X 7 X 5
I X 3 I2	+ I X 6 2		* X 3 X 4 + X 6 X *

X 4 X 3 + X 7 X 6   | Х 8 2 + | X 7 I² + | X 4 2 J

Вычисляя отрицательные собственные значения матрицы (8), мы можем определить временную зависимость параметра перепутывания кубитов. Результаты численных расчетов пара-

метра перепутывания (6) для начального состояния вида (2) и различных значений амплитуд поляризованных атомов 0 1 и О 2 и параметров штарковского сдвига Р 2 и в 1 представлены на рис. 1. На рисунках хорошо видно, что параметр перепутывания атомов меняется периодически, при этом период осцилляций зависит от параметров штарковских сдвигов и степени атомной когерентности. Особо можно отметить резкое увеличение максимальной степени атомного перепутывания при увеличении параметров штарковского сдвига. Расчеты показывают, что уже для значений Р 1 = в « 2 g , степень перепу-

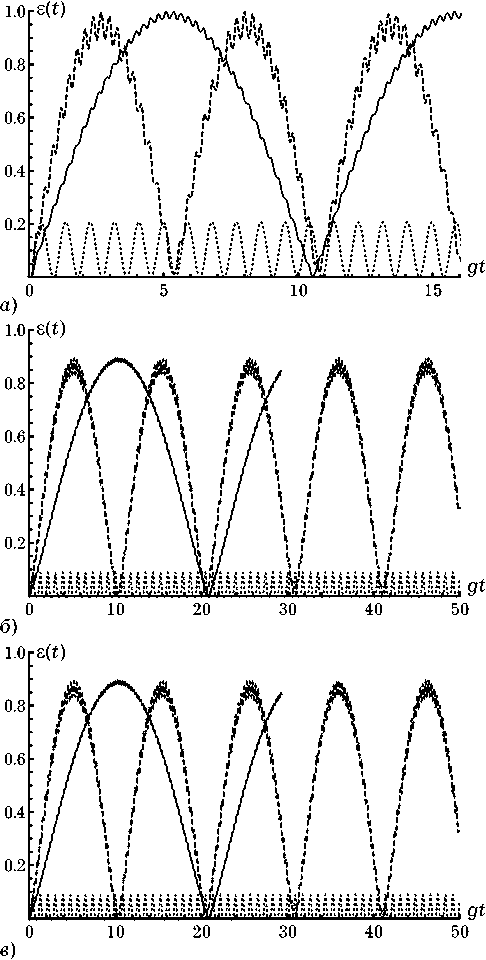
Рис. 2. Временная зависимость параметра перепутывания для начального состояния вида (9) и параметров штарковского сдвига β ₁= β ₂= 0 (точечные линии), β ₁= β ₂= 5 g (штриховые линии) и β ₁= β ₂= 10 g (сплошные линии). Амплитуды поляризованных атомов θ ₁ = π /2, θ ₂ = 0 ( а ), θ ₁ = π /4, θ ₂ = π /4 ( б ) и θ ₁ = π /4, θ ₂ = -π /4 (в). Разность фаз ∆ϕ = 0

тывания атомов достигает максимального значения. Таким образом динамических штарковский сдвиг энергетических уровней может использоваться для того, чтобы эффективно управлять и контролировать перепутывание двух первоначально распутанных кубитов. Сам же штарков-ский сдвиг уровней, как отмечалось уже выше, можно легко контролировать, изменяя величину расстройки между удвоенной частотой резонаторной моды и частотой атомного перехода.

Рассмотрим также динамику параметра перепутывания для других начальных чисел фото- нов в резонаторной моде. В случае одного и двух начальных фотонов в моде начальные состояния системы можно представить в виде

|Ψ(0)〉 =|ΨA1(0)〉 |ΨA2(0)〉 |1〉

и

|Ψ(0)〉 =|ΨA1(0)〉 |ΨA2(0)〉 |2〉.(10)

Временные волновые функции, соответствующие начальным состояниям (9) и (10) можно представить в виде

| Ψ(t)〉 = X1| +,+;1〉+X2| +,-;1〉+X3| -,+;1〉+ +X4| -,-;1〉+X5| +,-;3〉+X6| -,+;3〉+

+ X ₇| - , - ;3 〉+ X ₈| - , - ;5 〉

и

| Ψ ( t ) 〉 = X 1 | + , + ;2 〉+ X 2 | + , - ;2 〉+ X 3 | - , + ;2 〉+

+ X ₄| - , - ;2 〉+ X ₅| + , - ;4 〉+ X ₆| - , + ;4 〉+

+ X ₇| - , - ;4 〉+ X ₈| - , - ;6 〉+ X ₉| + , + ;0 〉+

+X10 | +,-;0〉+X11 | -, +; 0〉 соответственно.

Компьютерное моделирование временной зависимости параметра перепутывания (6) для состояний, описываемых волновыми функциями (11) и (12) было проведено на основе схемы, описанной в предыдущем разделе. Результаты численных расчетов параметра перепутывания (6) для начальных состояний (9) и (10) в случае различных значений амплитуд поляризованных атомов θ ₁ и θ ₂ и параметров штарковского сдвига β ₂ и β ₁ представлены на рис. 2 и 3 соответственно. Хорошо видно из сравнения рис. 1–3, что степень атомной когерентности оказывает существенное влияние на характер эволюции атомного перепутывания. При этом, как и для вакуумного состояния поля, для начальных состояний (9) и (10) наличие штарковского сдвига приводит к существенному увеличению перепутывания атомов. Таким образом, вывод о возможности использования штарковского сдига для контроля за степенью перепутывания атомов остается верным и для других когерентных неперепутанных состояний рассматриваемой системы.

В заключение отметим, что в настоящей работе мы исследовали временную динамику перепутывания двух двухуровневых атомов, взаимодействующих с квантовым электромагнитным полем посредством вырожденных двухфотонных переходов, с учетом штарковского сдига энергетических уровней атомов. При этом рассмотрена ситуация, когда атомы приготовлены в

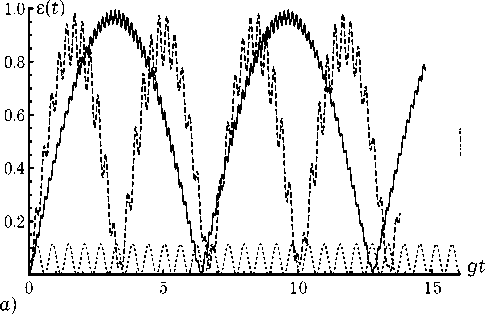
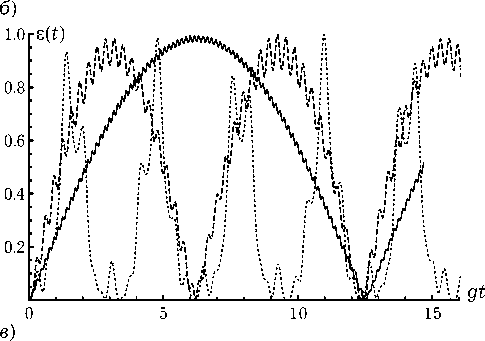
Рис. 3. Временная зависимость параметра перепутывания для начального состояния вида (10) и параметров штарковского сдвига β ₁= β ₂= 0 (точечные линии), β ₁= β ₂= 5 g (штриховые линии) и β ₁= β ₂= 10 g (сплошные линии). Амплитуды поляризованных атомов θ ₁ = π /2, θ ₂ = 0 ( а ), θ ₁ = π /4, θ ₂ = π /4 ( б ) и θ ₁ = π / 4, θ ₂ = -π /4 ( в ). Разность фаз ∆ϕ = 0

начальный момент времени в неперепутанных когерентных состояниях, а поле – в фоков-ских состояниях: без фотонов, с одним и двумя фотонами. Между атомами отсутствует прямое взаимодействие. Полученные нами результаты показывают, что динамика атомной перепутанности может эффективно контролироваться с помощью штарковского сдига и степени атомной когерентности.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ.