Влияние биметаллической оболочки и вращения на взаимодействие ударника с металлокерамической полубесконечной преградой

Процесс взаимодействия ударника с преградой и его результат зависят от многих факторов: физикомеханических свойств материалов тел, скорости удара, геометрических параметров, конструктивных особенностей ударника и преграды. В настоящее время численное моделирование является одним из основных инструментов, позволяющих проводить широкие параметрические исследования и прогнозировать влияние различных факторов на этот высокоскоростной процесс. При этом эксперимент необходим для подтверждения адекватности используемых математических моделей и численных алгоритмов.

При выполнении опытов по изучению поведения материалов при высоких скоростях деформирования применяются ударники разных конструкций: безоболочечные, когда ударник представляет собой монолитное тело из одного материала, и оболочечные, когда ударник состоит из сердечника, заключенного в оболочку, образуемую одним или двумя слоями материала. Влиянию оболочки на взаимодействие ударника с преградами посвящен ряд экспериментальных исследований [1 –6] . В [1] показано, что конструкция ударника (наличие оболочки, наполнителя) влияет на его баллистические характеристики и проникающую способность. Оценке роли оболочки в ударном процессе в зависимости от материалов сердечника, оболочки и преграды посвящены работы Crouch и др. [2] , Hazell и др. [3] , Forrestal и др. [4] и Roberts и др. [5] . Анализ результатов свидетельствует, что степень влияния оболочки на проникание обусловливается материалами взаимодействующих тел. Так, в [4] показано, что оболочка мало сказывается на проникании высокопрочного сердечника в алюминиевую преграду. Иная картина наблюдается, если ударник встречается с керамической преградой [2, 3, 5, 6] , в этом случае роль оболочки существенна. В работе [2] установлено, что стальная оболочка ударника с сердечником из мягкой стали увеличивает проникающую способность ударника при пробитии преграды из карбида бора. При ударе о керамику сердечника без оболочки происходит его обширное эрозионное разрушение и, как следствие, потеря кинетической энергии.

Предполагается, что существуют два механизма, обеспечивающих увеличение проникающей способности оболочечного ударника: во-первых, оболочка снижает радиальный импульс сердечника в контактной области, что позволяет сохранить осевой импульс; во-вторых, оболочка повреждает керамику до ее соприкосновения с сердечником [7] . В работе [8] представлены результаты комплексного (экспериментального и численного) исследования проникания сердечника из карбида вольфрама без оболочки и в оболочке в алюминиевые и стальные преграды конечной толщины. Как показали эксперименты, остаточная скорость оболочечного ударника после перфорации преграды почти на 50% превышает остаточную скорость сердечника без оболочки. Таким образом, из анализа экспериментальных данных следует, что при численном моделировании для получения адекватных результатов и успешного прогнозирования физико-механических свойств ударяющихся тел в конструкциях ударника необходимо принимать во внимание и оболочки, и наполнители [9, 10] . Но следует отметить, что учет конструктивных особенностей существенно усложняет задачу. Поэтому иногда в работах, посвященных

Статья опубликована в открытом доступе по лицензии CC BY 4.0

численному моделированию высокоскоростного воздействия оболочечных ударников, наличием оболочки и наполнителя пренебрегают, рассматривают только взаимодействие сердечника [11] или считают, что ударник полностью состоит из материала сердечника [12] .

Керамические материалы на основе карбида бора (B 4 C) обладают высокими механическими характеристиками, прежде всего такими как твердость, износостойкость, высокие модули упругости. Относительно низкая плотность в сочетании с высокими механическими характеристиками обусловливают широкое использование этого материала в качестве элементов противоударных защитных конструкций [2–8, 10, 13]. Исследованию разнообразных свойств карбида бора в области высоких давлений, возникающих при ударных воздействиях, посвящено много работ [13 –20] . Свойства керамики (B ₄ C) и ее поведение в ударных волнах и при высоких скоростях деформирования существенно зависит от технологии ее получения [15 –20] . Например, при высоких давлениях в карбиде бора могут происходить фазовые переходы, что выражается в изломах на кривой ударной адиабаты [15, 16] . Изломы свидетельствуют о повышении (до 15 ГПа) предела текучести и уменьшении удельного объема при фазовом превращении в области давлений 40–50 ГПа, при этом точно определить давление фазового перехода ударно-сжатого карбида бора затруднительно в связи с большим разбросом экспериментальных данных, обусловленных способом изготовления образцов [16] . Особенностью карбида бора также является низкая прочность на растяжение.

Еще один фактор, влияние которого обсуждается в настоящей работе — вращение ударника. Для метания в баллистических экспериментах используются как нарезные стволы, при выходе из которых ударник приобретает поступательное движение и вращение вокруг своей продольной оси, так и гладкоствольные установки, не создающие вращения ударника. Иногда прибегают к обратной баллистике [2] , осуществляют метание преграды, а ударник закреплен и неподвижен. В этом случае вращение ударника также отсутствует.

Как правило, при реализации вычислительных экспериментов вращением ударника пренебрегают. Отчасти это связано с предположением, что при взаимодействии вращающегося ударника основное влияние будет оказывать трение. Но эксперименты Джозефа Краффта по исследованию проникающей способности вращающихся и невращающихся ударников [19] выявили, что вклад трения несущественен: он не превышает 3–4% при низкоскоростном ударе и менее 1% при высокоскоростном. В дальнейшем, основываясь на выводах работы [19] , влиянием вращения на процесс проникания ударников в преграды пренебрегают (см. [20] ). Но исключение из рассмотрения вращения не всегда корректно. Как показано в [21, 22] , в результате вращательного движения в ударнике еще до момента встречи с преградой формируется напряженно-деформированное состояние, которое может повлиять на процесс его взаимодействия с преградой и зависит от физико-механических свойств материалов ударника и преграды, геометрических и кинематических параметров ударника.

• 2.    Математическая постановка задачи

  • 2.1.    Основные уравнения математической модели

Движение участвующих в ударном процессе тел рассматривается в адиабатической постановке. Система уравнений, описывающих нестационарные движения сжимаемой среды в произвольной системе координат x^l (i =1,2,3) включает уравнения [21, 22] :

– неразрывности

– движения

pa^k = Vj ^ik + F ^k ,

где a^k = —— + и VU , У _г а ^k ∂t

– энергии

ik k im m ik ^j ,i ^{+ Г} im ^{j  + Г} im & ^;

dE dt

= - j j e ij . ^ρ

В (1) – (3) приняты обозначения: t — время; ρ — плотность среды; υ ⁱ — компоненты вектора скорости; σ ^ij — контравариантные компоненты симметричного тензора напряжений; F ^k — компоненты вектора массовых сил; Γ _i ^k _j — символы Кристоффеля; E — удельная внутренняя энергия; e ij — компоненты симметричного тензора скоростей деформаций: e ij = (V i U j + V j ui)/2; компоненты тензора напряжений представляются в виде суммы девиаторной — S ^ki , и шаровой (давления) — P , частей:

jij = Pgi + Sj, где gij — компоненты метрического тензора.

Давление в металлических материалах определяется, согласно уравнению Ми–Грюнайзена, как функция удельной внутренней энергии E и плотности ρ :

P = XKn n=1

V

V 0

?! +K o pE,

где K 0 , Kn — константы материала, V 0 — начальный удельный объем, V — текущий удельный объем. Для расчета давления в керамике B ₄ C используется уравнение состояния [23] :

P=

V0 - V exp 4b-----

V 0

ρ 0 c 0²

4b

При этом ρ 0 — начальная плотность; V 0 и V — начальный и текущий удельные объемы; c 0 и b — коэффициенты ударной адиабаты: D = c ₀ + bu m, D — скорость ударной волны, u m — массовая скорость. Исследуемым далее скоростям взаимодействия отвечают значения коэффициентов ударной адиабаты [15, 16] : c 0 =10.2 км/с, b =0.85.

Предположив, что для рассматриваемых материалов справедлив принцип минимума работы истинных напряжений на приращениях пластических деформаций, запишем связь компонент тензора скоростей деформаций и девиатора напряжений в виде:

ij

2G(gimgjkemk -gmemkgi/3) = — + ASij (A> 0).

Здесь G — модуль сдвига; поправка на поворот определяется с помощью коротационной производной Яуманна:

ij ij im      kj jmik

—ргг = ,. g ^mkS j - gj ^mkS , Dt dt где Uij = (ViUj -Vjui)/2. Если выполняется условие Мизеса:

Si Sj < 2^2/3, то материал ведет себя упруго (A = 0), если оно нарушается, то поведение пластическое (A > 0). Динамический предел текучести σd в (8) в общем случае может быть функцией скоростей деформаций, давления и температуры. Для рассматриваемого диапазона скоростей динамический предел текучести полагаем постоянным.

Посчитав, что пластическая деформация не приводит к изменению объема, в качестве локального критерия разрушения металлов выберем предельную величину интенсивности пластических деформаций [24] :

e u = “3“ q T-T i ,

где T 1 , T 2 — первый и второй инварианты тензора деформаций, значение e u , как и σ d , полагаем постоянным. Разрушение керамики B 4 C будем оценивать с помощью деформационного критерия и с учетом различия ее прочности при сжатии и растяжении [12, 25, 26] :

£c <£ц <£t (i = 1,2,3), где εc — предел прочности на сжатие, εt — предел прочности на растяжение. При нарушении условия (10) материал полагается разрушенным.

• 2.2.    Постановка задачи

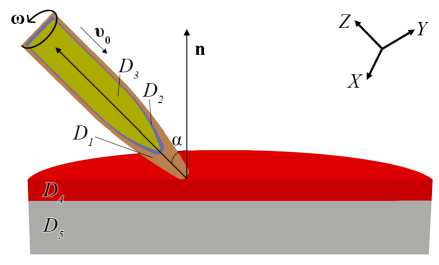
Задача формулируется в декартовых координатах X Y Z (x ¹ = x, x ² = y, x ³ = z, r j = 0, o ^ij = o ij , g^{l j} = 8 ij , где S ij — символ Кронекера, i,j = 1,2,3). Моделируется нормальное (a = 0 ° ) и косое (a = 0 ° ) взаимодействие оживальных (с формой головной части, промежуточной между конусом и эллипсоидом) ударников с двухслойной преградой (Рис. 1) . Ударник состоит из высокопрочного стального сердечника (область D 3 ), латунной

( а )

Рис. 1. Схема к постановке задачи

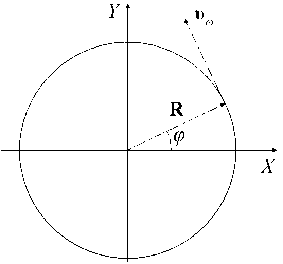
оболочки (D 2 ) и свинцового наполнителя (D i ). Преграда представляет собой двухслойную конструкцию, верхний слой которой изготовлен из карбида бора B 4 C (область D 4 ), а нижний — из алюминия (D ₅ ). Вектор скорости ударника и ₀ и его ось симметрии в начальный момент времени совпадают с осью Z и образуют с нормалью к преграде угол а. Помимо поступательного движения со скоростью u _q , ударник вращается вокруг своей оси с начальной угловой скоростью | й ₀| = 2nv, где v — частота вращения, показывающая число оборотов ударника в секунду. Линейная скорость вращательного движения точек ударника представляется как векторное произведение:

иш = и xR, где R — радиус-вектор произвольной точки. Проекции вектора скорости υω на оси X и Y определяются соотношениями: и1 = |иш |sinф и и3 = |иш |cosф (Рис. 1 б). Проекция иш на ось Z равняется нулю: и3 = 0.

Для уравнений (1) – (11) ставится задача с начальными и граничными условиями:

р                              aj = P = E = 0|(xi)£Dk   (i = 1,2,3),   (k = 1,5);

и1 = |иш |sinф|(xi)eDk,   U2 = |иш |cosф|(xi)eDk,   U3 = -|uq|   (i,k = 1,2,3);

ui = 0|(xi )eDk (i = 1,2,3),   (k = 3,4,5);

P = Pi\(xi)EDk (i = 1,2,3), (к = Ш

– на контактных поверхностях между всеми областями Dk (k = 1, 5) реализуется условие скольжения без трения

T ⁺= T~. T⁺= -   T⁺= T^-=0. v⁺ = ^-:

nn nn ,    nτ nτ ns ns , n n ;

– на свободных поверхностях задается условие отсутствия напряжений

Tnn=Tns=Tnτ=0

.

Здесь n — единичный вектор нормали к поверхности в рассматриваемой точке; τ и s — взаимно перпендикулярные единичные векторы в плоскости, касательной к поверхности в этой точке; T n — вектор силы на площадке с нормалью n . Нижние индексы у векторов T _n и υ означают проекции на соответствующие векторы базиса. Система уравнений (1) – (11) совместно с начальными и граничными условиями (12) – (17) полностью определяет краевую задачу.

Геометрические параметры и материалы ударника полностью соответствуют данным, приведенным в [25, 26] : материалом сердечника является высокопрочная сталь твердостью по Роквеллу 63 HRC, плотностью P 0 = 7800 кг/м ³ с динамическим пределом текучести a d = 2.7 ГПа, диаметр сердечника D c = 6.172 мм, длина сердечника L _c = 27.43 мм, L _c /D _c = 4.44; диаметр ударника с биметаллической оболочкой D _s = 7.836 мм, длина ударника L s = 35.31 мм, L s /D s = 4.5, материал внешней оболочки — латунь плотностью р ₀ = 8920 кг/м ³ с пределом текучести a d = 100 МПа, наполнитель состоит из свинца плотностью р ₀ = 11400 кг/м ³ с пределом текучести σ _d = 10 МПа. Полный вес ударника составляет 10.8 г, вес стального сердечника — 5.3 г.

Толщина верхнего слоя двухслойной преграды равняется 3.75 мм, материал — карбид бора B ₄ C плотностью P 0 = 2490 кг/м ³ с динамическим пределом текучести a d =15 ГПа [15, 16] и пределами прочности s c = - 0.27 и e t = 0.1 [12, 24, 25] ; нижний слой преграды — массив из алюминия Al 5083 плотностью р ₀ = 2640 кг/м ³ с пределом текучести σd = 120 МПа.

Начальная скорость ударника в расчетах соответствует экспериментальной [25, 26] | u _q | = 841 м/с, частота вращения ударника v = 0 ^ 10000 об/с. Рассмотрен диапазон углов взаимодействия а = 0 ^ 45 ° . Задача решается численно, методом конечных элементов с использованием авторского программного 3D комплекса EFES 2.0 [21, 22] .

• 3.    Обсуждение результатов

Для оценки эффективности керамических преград широко применяется метод DOP (Depth-Of-Penetration) [25 –34] , основанный на сравнении результатов метания ударника как в монолитную металлическую, так и в двухслойную преграду, у которой верхний слой — керамическая пластина, нижний — металлический массив. По соотношению глубин проникания ударника в слоистую металлокерамическую и монолитную преграды делается вывод об эффективности защитных свойств керамической пластины. Несомненным достоинством метода DOP является простота и надежность, поскольку глубина проникания может быть измерена точно. Также метод DOP может применяться для валидации математических моделей и численных алгоритмов.

В таблице 1 приведены глубины кратеров, образованных в массивной алюминиевой преграде при разной толщине керамического слоя, полученные в эксперименте [25, 26] и в расчете. С учетом того, что в экспериментах для метания ударника использованы нарезные стволы Манна, в которых ударнику сообщается вращательное движение с частотой около 3000 об/с [35] , в тестовых расчетах ударник тоже вращается с частотой ν= 3000 об/с. Наблюдается хорошее согласование результатов, относительная погрешность δ не превышает 8%, что позволяет сделать вывод об адекватности и математической модели, и численного алгоритма. Далее обсуждаются авторские

Таблица 1. Свойства материала

Толщина керамического слоя, мм Глубина кратера, мм Погрешность δ, % эксперимент расчет 1.25 40.6 37.8 6.9 2.5 33.4 33.2 0.6 3.75 10.1 9.3 7.9 5 0 0 0 результаты параметрических численных исследований влияния биметаллической оболочки и вращения ударника на процесс его взаимодействия с металлокерамической преградой при нормальном (а = 0°) и косом (а = 0°) ударе. Толщина лицевого слоя керамики B4C составляет 3.75 мм, начальная скорость ударника соответствует экспериментальной |υ0| =841 м/с.

На рисунке 2 в последовательные моменты времени в сечении ZX приведены расчетные конфигурации взаимодействия с металлокерамической преградой высокопрочного стального сердечника (без оболочки и наполнителя) без вращения (Рис. 2а ) и с вращением вокруг своей оси (Рис. 2б ). Как видно, сердечник не проникает в алюминиевую преграду, наблюдается его отскок. Полное пробитие керамического слоя не происходит, в обоих случаях сердечник образует в нем кратер глубиной 2.7 мм. При этом остаточная длина сердечника равняется 10.1 мм, что составляет 37% от его начальной длины. Конфигурации свидетельствуют об активном эрозионном разрушении сердечника при проникании в керамический слой, что приводит к снижению его кинетической энергии и, как следствие, к уменьшению проникающей способности.

( а )

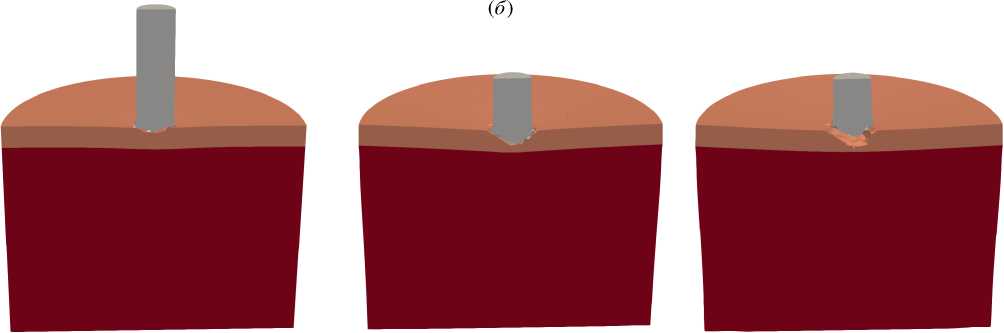
Рис. 2. Конфигурации сердечника и преграды в сечении ZX через 10, 30 и 100 мкс при ударе под углом а = 0 ° и разной частоте вращения сердечника ν , об/с: 0 ( а ), 3000 ( б )

Рисунок 3 иллюстрирует взаимодействие полного ударника (сердечник+оболочка+наполнитель) без вращения (Рис. 3а ) и с вращением (Рис. 3б ). Сравнение результатов моделирования процесса при ударе сердечником (Рис. 2) и полным ударником (Рис. 3) показывает, что на начальной стадии (до t= 10 мкс) оболочка способствует уменьшению объема эрозионного разрушения в сердечнике и сохранению формы его головной части. В процессе внедрения ударника в преграду оболочка «снимается» с сердечника. В случае полного ударника керамический слой перфорируется, при этом невращающийся ударник (ν = 0) погружается в алюминиевую преграду на 10.9 мм, а вращающийся (ν = 3000 об/с) — на 9.3 мм.

Таким образом, при рассмотренных условиях проникающая способность невращающегося ударника на 15% выше. Снижение глубины проникания при вращении обусловлено формированием во вращающемся ударнике

( а )

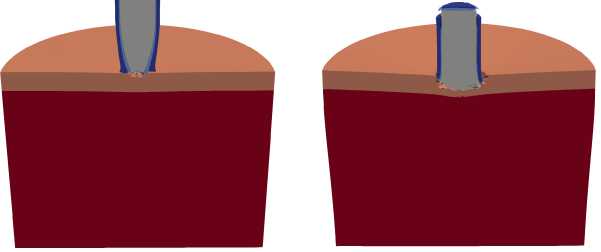
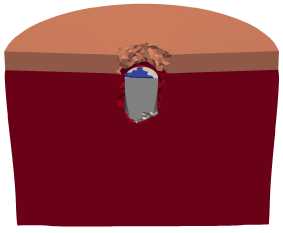
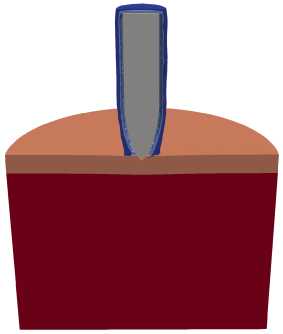
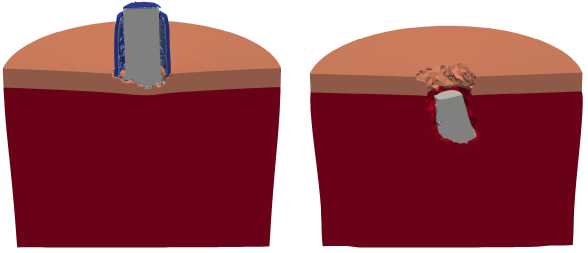
Рис. 3. Конфигурации полного ударника и преграды в сечении ZX через 10, 30 и 100 мкс при ударе под углом а = 0 ° и разной частоте вращения ударника ν , об/с: 0 ( а ), 3000 ( б )

напряженно-деформированным состояния (НДС). В ударнике возникают как нормальные напряжения, вызванные центробежными силами, так и сдвиговые напряжения, обусловленные различием линейных скоростей (10) в точках ударника, расположенных на разных расстояниях от его оси вращения [21, 22] . При этом максимальные значения сдвиговых напряжений достигаются вблизи боковой поверхности сердечника. В результате происходит интенсификация контактного взаимодействия ударника с керамическим слоем, что увеличивает эрозионное разрушение сердечника и уменьшает кинетическую энергию ударника. В то же время уровень НДС при ν = 3000 об/с не оказывает заметного влияния на разрушение керамического слоя. Также при сравнении степени проникания сердечника (Рис. 2) и полного ударника (Рис. 3) необходимо учитывать очевидный факт, что масса сердечника составляет лишь 49% от массы полного ударника, соответственно, его кинетическая энергия также на 49% меньше кинетической энергии полного ударника.

С увеличением частоты вращения до ν= 10000 об/с наблюдается интенсивный радиальный разлет фрагментов разрушающейся металлической оболочки (Рис. 4) . В этом случае глубина кратера в алюминиевой преграде составляет 11.5 мм, что больше глубины кратера на 5.5% при ν=0 и на 23.6% при ν = 3000 об/с. Это обусловлено тем, что при ν = 10000 об/с образовавшееся в сердечнике НДС способствует интенсификации эрозии керамического слоя в контактной зоне, и к моменту времени t = 30 мкс стальной сердечник практически полностью разрушает керамический слой. В случае же невращающегося ударника (Рис. 3а ) и частоты вращения ν = 3000 об/с (Рис. 3б ) перед сердечником в момент времени t = 30 мкс находится неразрушенный слой керамики толщиной 1.7 мм.

Анализ влияния вращения ударника на разрушение материалов в контактной зоне показывает, что с увеличением скорости вращения растет уровень сдвиговых напряжений на контактной границе ударника с керамическим слоем. Следствием этого является интенсификация эрозионного разрушения сердечника. При частотах ниже 3000 об/с керамика не разрушается, но с увеличением скорости вращения ударника до ν= 10000 об/с керамический слой начинает активно крошиться, и ударник проникает на большую глубину. Таким образом, увеличение частоты вращения ударника с 3000 до 10000 об/с приводит к увеличению проникающей способности оболочечного ударника при взаимодействии с металлокерамической преградой.

Для проверки корректности моделирования полного ударника (сердечник+металлическая оболочка+наполнитель) проведены расчеты для нормального взаимодействия монолитного ударника с металлокерамической преградой. Монолитный ударник полагался стальным (как сердечник) и имел такую же геометрию (диаметр, длину, форму головной части), как у полного ударника. На рисунке 5 показаны итоговые конфигурации монолитного стального ударника и преграды для частот вращения 0, 3000 и 10000 об/с. Начальная

Рис. 4. Конфигурации полного ударника и преграды в сечении ZX через 10, 30 и 100 мкс при ударе под углом а = 0 ° и частоте вращения ударника ν = 10000 об/с

( а )                                                  ( б )                                                  ( в )

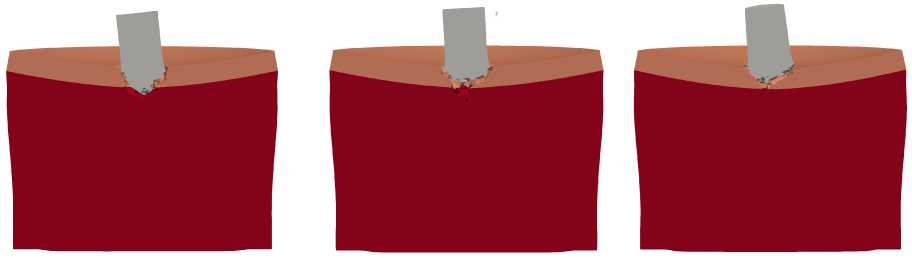
Рис. 5. Конфигурации монолитного (стального) ударника и преграды в сечении ZX в момент времени t = 100 мкс при ударе под углом а = 0 ° и разной частоте вращения ударника v , об/с: 0 ( а ), 3000 ( б ), (10000 ( в )

скорость также равнялась 841 м/с. Монолитный стальной ударник имел массу на 5.7% меньше, чем у полного ударника (и, соответственно, его кинетическая энергия была меньше на 5.7%). При этом глубины кратеров в алюминиевой преграде существенно отличаются от соответствующих глубин проникания полного ударника и составляют лишь 3, 2 и 0 мм для частот вращения 0, 3000 и 10000 об/с соответственно. Из данного результата следует, что при моделировании взаимодействия полного ударника с металлокерамической преградой необходимо учитывать и оболочку, и наполнитель.

Также проведены исследования косого взаимодействия сердечника, полного ударника и монолитного стального ударника с металлокерамической преградой. Рисунок 6 содержит конфигурации сердечника и преграды при ударе под углом а = 30 ^о (напомним, что а — угол между продольной осью ударника и нормалью к преграде). Расчеты показывают, что уже при а = 30 ^о происходит рикошет сердечника от металлокерамической преграды, при этом повреждается только керамический слой, в котором образуется неглубокий кратер. Для случая вращающегося сердечника (Рис. 6б ) поврежденная зона керамического слоя несколько протяженнее. Это обусловлено ударом тыльной части сердечника по преграде при повторном рикошете. При отсутствии керамического слоя и углах а <  45 ^о рикошет сердечника не наблюдается (Рис. 7) . Видно, что при частотах вращения 0 и 3000 об/с сердечник

( а )                                                  ( б )

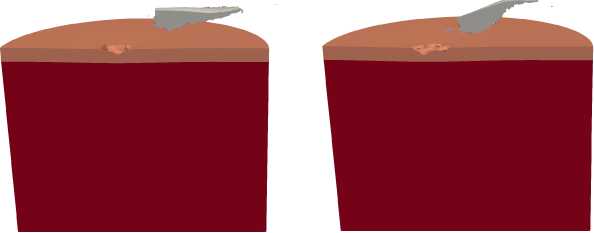
Рис. 6. Конфигурации сердечника и преграды в сечении ZX после момента времени t = 100 мкс при ударе под углом а = 30 ° и разной частоте вращения сердечника v , об/с: 0 ( а ), 3000 ( б )

сохраняет начальную траекторию движения по мере проникания в преграду (Рис. 7а , б ), но при ν = 10000 об/с (Рис. 7в ) при контакте с преградой он поворачивается (как при рикошете) и дальше движется в плоскости ZX преграды плашмя, контактирует с ней боковой поверхностью; его скорость падает до нуля. В этом случае размер образованного в преграде кратера в сечении ZXпрактическиравен длине внедряющегося сердечника.

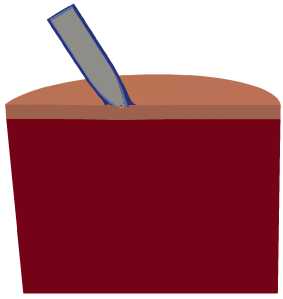
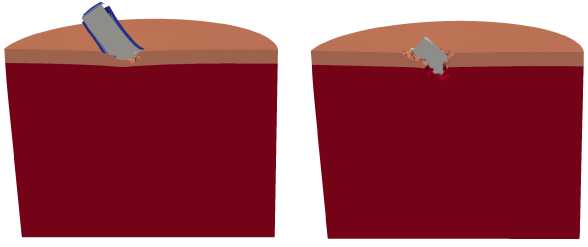
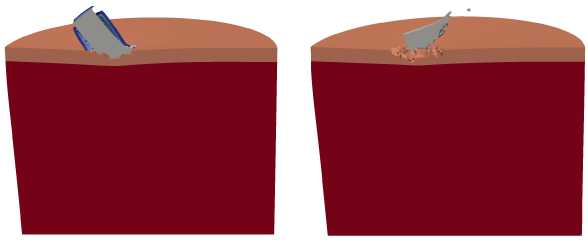
На рисунке 8 приведены конфигурации полного ударника при взаимодействии с металлокерамической преграды под углом а = 30 ^о и с частотами вращения 0, 3000 и 10000 об/с. Кратер глубиной 3 мм в алюминиевой

( а )                                                  ( б )                                                  ( в )

Рис. 7. Конфигурации сердечника и алюминиевой преграды в сечении ZX после момента времени t = 200 мкс при ударе под углом а = 45 ° и разной частоте вращения сердечника v , об/с: 0 ( а ), 3000 ( б ), 10000 ( в )

( а )

( б )

( в )

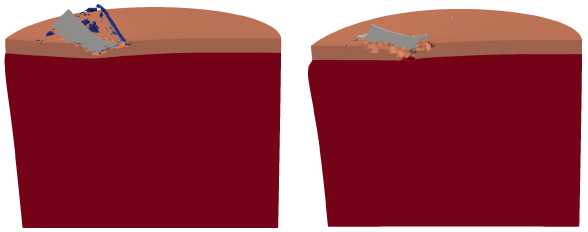
Рис. 8. Конфигурации полного ударника и преграды в сечении ZX в моменты времени 10, 30 и 100 мкс при ударе под углом а = 30 ° и разной частоте вращения ударника v , об/с: 0 ( а ), 3000 ( б ), 10000 ( в )

преграде образуется только в случае невращающегося ударника (Рис. 8а ). При проникании вращающегося ударника (Рис. 8б , в ) происходит рикошет без разрушения алюминиевого слоя преграды.

На рисунке 9 представлены кривые изменения во времени угла αυ между нормалью к металлокерамической преграде и вектором скорости центра масс полного ударника и сердечника при косом ударе под углом а = 30 ^о (Рис. 9а ) и а = 45 ^о (Рис. 9б ). Значения а _и >  90 ^о соответствуют рикошету ударника. Как следует из графиков, рикошет не возникает только при невращающемся полном ударнике и угле взаимодействия а = 30 ^о (кривая 1 , Рис. 9а ). Во всех других случаях наблюдается быстрое увеличение значения α _υ и рикошет как сердечника, так и полного ударника, причем увеличение α _υ для сердечника происходит раньше, чем для полного ударника. Этот результат качественно согласуется с ранее полученными данными [21, 22] .

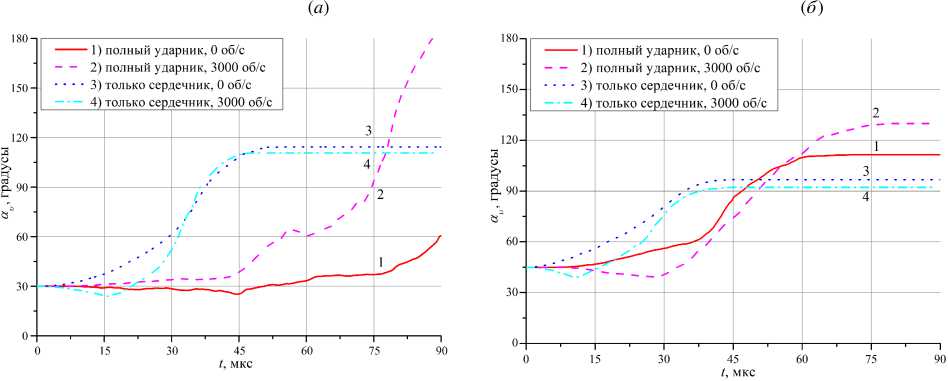
Рис. 9. Изменение во времени величины угла α υ между нормалью к преграде и вектором скорости центра масс ударного инструмента при косом ударе под углом а = 30 ° ( а ) и а = 45 ° ( б )

В таблице 2 приведены данные, характеризующие итог взаимодействия сердечника, полного ударника и монолитного стального ударника с металлокерамической преградой — глубина кратера в алюминиевой преграде и состояние ударника после взаимодействия (торможение, отскок, рикошет). Анализ результатов показывает, что при валидации математической модели и вычислительного алгоритма необходимо учитывать реальную конструкцию ударного инструмента (в данном случае наличие металлической оболочки и наполнителя) и кинематические условия (его вращение).

Таблица 2. К сравнению результатов косого удара с начальной скоростью 841 м/с по алюминиевой преграде с толщиной керамического слоя 3.75 мм

Ударный инструмент	Частота вращения v , об/с	Удар под углом α , град
		0		30		45
		глубина кратера, мм	состояние инструмента	глубина кратера, мм	состояние инструмента	глубина кратера, мм	состояние инструмента
Сердечник	0	0	отскок	0	рикошет	0	рикошет
	3000	0	отскок	0	рикошет	0	рикошет
Полный ударник	0	10.9	торможение	3	торможение	0	рикошет
	3000	9.3	торможение	0	рикошет	0	рикошет
	10000	11.5	торможение	0	рикошет	0	рикошет
Стальной монолитный ударник	0	3	отскок	0	рикошет	0	рикошет
	3000	2	отскок	0	рикошет	0	рикошет
	10000	0	отскок	0	рикошет	0	рикошет

• 4.    Выводы

Анализ полученных результатов позволяет сделать выводы.

• 1.    Предложенная математическая модель адекватно описывает процесс взаимодействия ударника с металлокерамической преградой и позволяет проводить параметрические исследования влияния кинематических, геометрических и конструктивных факторов на процесс.

• 2.    Для рассмотренных условий взаимодействия конструктивные элементы полного ударника (оболочка, наполнитель) оказывают существенное влияние на его взаимодействие с преградой. Для адекватного моделирования и прогнозных расчетов необходимо учитывать реальную конструкцию ударного инструмента.

• 3.    Расчеты подтвердили, что оболочка и наполнитель обеспечивают сохранность сердечника на начальном этапе процесса взаимодействия ударника с металлокерамической преградой.

• 4.    В присутствии керамического слоя наблюдается рикошет сердечника уже при угле взаимодействия а = 30 ° .

• 5.    Вращение полного ударника может оказывать существенное влияние на разрушение участвующих в ударном процессе тел и на состояние ударного инструмента. При этом до скоростей вращения 3000 об/с интенсифицируется эрозионное разрушение сердечника, что снижает его проникающую способность. С увеличением частоты вращения до 10000 об/с большее разрушение испытывает керамический слой преграды, что приводит к увеличению глубины проникания сердечника. В то же время при косом ударе вращение полного ударника способствует его рикошету.

Исследование выполнено при поддержке Программы развития Томского государственного университета (Приоритет–2030). Математическая модель и программный комплекс EFES созданы в рамках государственного задания ИФПМ СО РАН, проект FWRW-2021-0002.