Влияние дифракции на изображения, согласованные с вытянутыми сфероидальными волновыми функциями

Вытянутые сфероидальные волновые функции (ВСВФ) известны в оптике, прежде всего, как моды оптических систем с ограниченной апертурой и проходящие через такие оптические системы без искажений [1-4].

ВСВФ представляют собой полный набор функций с ограниченной спектральной полосой, которые ортогональны как на данном конечном интервале, так и на бесконечном интервале [5]. Таким образом, бесконечным рядом по ВСВФ можно представить любое световое поле. Суперпозиция ВСВФ, аппроксимирующая некоторое световое распределение, будет обладать модовым характером при прохождении через оптические линзовые системы с ограниченной апертурой. То есть, изображение будет устойчиво к дифракционным эффектам, связанным с ограниченными размерами апертуры оптической системы.

Заметим, что разложение поля или изображения, сформированного оптической линзовой системой по базису ВСВФ является оптимальной процедурой в смысле минимального количества слагаемых разложения, число которых равно числу степеней свободы оптической системы по Шеннону [6, 7].

В [8] высказано предположение, что обобщенные двумерные ВСВФ [9] обладают также свойством самовоспроизведения при распространении в пространстве, то есть они являются собственными функциями оператора дифракции Френеля от ограниченной апертуры.

В данной работе с помощью численного моделирования исследуется устойчивость одномерных ВСВФ к преобразованию Френеля. Кроме того, исследуются другие свойства ВСВФ, важные для дифракционной оптики: инвариантность к преобразованию Фурье, устойчивость к диафрагмированию в объектной плоскости.

Также проведены численные эксперименты, моделирующие прохождение сигнала, представляющего собой суперпозицию ВСВФ, через линзовую систему с ограниченным зрачком в спектральной плоскости. Исследуется влияние размеров диафрагмы на точность передачи сигнала. Проводится сравнение с функциями Гаусса-Эрмита.

1.    Свойства ВСВФ, используемые в дифракционной оптике

После разделения трехмерного скалярного волнового уравнения в вытянутых сфероидальных координатах возникает дифференциальное уравнение [10]:

d _м 2х d V( x )        2 2 m / x

—(1 -x 'J + X-c x--у ,V(x) = 0, (1) dx          dx ^           1 - x 2 J которое имеет непрерывное вещественное решение Vx), ограниченное при любых x. С точностью до константы решение единственно. Здесь и далее: c – произвольное положительное число, m – неотрицательное целое. Для упрощения записи в дальнейшем будем опускать зависимость величин от c.

Обозначим специальные значения х , при которых существуют непрерывные решения через x mn , n = m , m +1… . Эти собственные значения могут быть так обозначены, поскольку 0< x m,_m< x m _m +i<- . Соответствующие им решения обозначим v m,A x )• Собственные функции v m,_n (x ) четные, если n-m - четное число и нечетные, если n-m – нечетное число. Также они имеют ровно n-m нулей на открытом интервале | x |<1.

Функции v m,n ( x ) известны [11, 12] как вытянутые сфероидальные волновые функции порядка m . Однако особый интерес представляют ВСВФ нулевого порядка. Благодаря ряду замечательных свойств они играют важную роль во многих прикладных задачах.

Функции v ₀,_n ( x ), которые далее будем обозначать просто v n ( x ), удовлетворяют интегральному уравнению [10]:

„     , .    1 sin [ c ( y - x )]        ,

^ n V n ⁽ У ) = J—,    v V n ⁽ x )d x ,

• - 1 ^{n (} У ^{- x} )

Г 2 c       1                  (2)

T /2 sin — ( У ^{- x} )

^ n V n ⁽ У ) = J —4r^ V n ⁽ x ^)d x ,

• - T /2    ^{п (} У ^{- x} )

где A n - собственные числа, 1 > X _o > X 1 > ... >  0. При этом собственные числа интегрального преобразования определяют количество энергии соответствующей собственной функции, концентрирующейся на данном ограниченном интервале. Собственные числа, близкие к единице, показывают, что данная ВСВФ имеет за пределами данного интервала малую долю энергии. Поведение A n как функции от n таково, что до некоторого n₀ =2 cI n собственные числа имеют значения близкие к единице, а после - резко спадают до нуля.

Используя (2) функция vn(x) можно продлить на все пространство [-да, да]. Рассмотрим преобразо- вание Фурье аналитического продолжения Vn(у) (при A, =1):

V - ( w ) = ^ [ V n ( У ) ] = J V , ( У ) exp ( - i2 n yw ) d у .   (3)

-to

to

J V n ⁽ x) V m ⁽ x ^)d x =

-to

Из (2) получаем:

to

= J V n ^{( x} )

-to

11 . . sin[ c ( x - t )] , _; JV m ( t )— ’-^d t ^A m - 1 ^{n ( x -} t )

d x =

’ , ( w ) = 3

2 c • 2 c V ₄ — sincl — x 1*ш„ ( x )

n nT VnT )

= 3

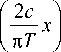
’ n ⁽ w ) = ⁿl — w ’ n ⁽ w )

где     sinc( x )=sin( n x )/ n x ,       *- знак     свертки,

^{n( x} ) =

1, | x | < 0,5 0, | x | > 0,5.

Таким образом, спектр V n ( x )

практически равен нулю вне интервала [ - w₀ , w₀ ]:

’ n ( w ) = ^п| ; w l’ n ⁽ w ), w 0 = -c ;.

V 2 w 0 J             n T

ВСВФ нулевого порядка являются собственными функциями преобразования Фурье на ограниченном интервале [3,10,13]:

a п ’ п ( У ) = J exp( icxy ) ’ - ( x )d x ,

- 1

^X n     ~ |^a n | ,

2 n

2 nX_n iⁿJ----- ’ n

c

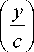
= J exp( ixy ) ’ _n ( x ) d x ,

- 1

с учетом комплексного сопряжения и замены переменных:

,      2Х_п    ( 2 ©

(-1)n J—-’»! — n у T ©о    V T ©o

T /2

J exp( - i2 n xw ) ’ _n ( x ) d x . (7)

- t /2

Используя правило нормировки, выбранное в [5]:

T /2

J ’ п ⁽ x ) ’ m ⁽ x ) dx = 5 mn X - ,

- T /2

+to

J ’ n ⁽ x ) ’ m ⁽ x ) dx = ⁵ mn , -to

и свойство (4), получаем выражение для преобразования Фурье на бесконечном интервале:

i

- п

T

A n 2 w o

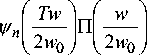
to

= J exp( - i 2 n xw V - ( x )d x

-to

и выражение для sinc-преобразования (2) на бесконечном интервале:

/ _А to sin [ c ( у - x )]    , . ,

V - ( У ) = J —/   , V - ( x )d x .           (10)

-to ^{n (} У ^{- x} )

Все перечисленные свойства взаимосвязаны и следуют один из другого. Например, из (2) и (10) следует свойство двойной ортогональности (8):

1 1

= "7  J ^V m ⁽ t )

^A m - 1

to

J V n ⁽ x )

-to

sin [ c ( t - x )] , d x n ( t - x )

d t =

₁ 1                               ₁

= Л J ^V m ⁽ t ^{) v} - ⁽ t ^)d t =Л ^A m S nm = ^ nm ^.

^A m - 1               ^A m

Также из (5), учитывая, что:

« * V n ⁽ У ) = J ^exp^{( - icx}У) V n ^{( x )d x} ,

- 1

V n ( x ) - действительные, можно получить (2):

J exp( icxy ) v , ( x )d x =

- 1

= J exp( lcxy ) — J exp( - icxt) V n ( t )d t d x =

- 1

^a - - 1

= — J V n ⁽ t ) J ^exp ^{[ icx (} У ^- t ^{) ] d x d} t =

^a n

- 1

= ^r J v - ⁽ t )

_ - 1

^{sin [} c ⁽ у ^- t ^{) ]} _d t =

^a n - 1

2 n 1

= — JV n ⁽ t ) a - c - 1

То сть,

c ( У - 1 )

sin [ c ( у - 1 )] , _{z 4}

—L---d t = a n V n ⁽ У ^). n ⁽ У ^- t )

¹         sin [ c ( у - 1 ) ]        ^- 1^{2 c} , , .      , ,

J V n ⁽ t ) —7 , , ^d t =   V n ⁽ У ) = ^A n V n ⁽ У ).

- 1 п ( у - 1 )         2 n

2. Численные результаты

Одним из важнейших свойств ВСВФ нулевого порядка из перечисленных в разделе 1, является инвариантность к преобразованию Фурье на ограниченном отрезке (5) - (7). То есть функция v n ( x ) воспроизводится в зоне дифракции Фраунгофера или в фокальной плоскости сферической линзы с точностью до коэффициента, определяемого размерами диафрагмы в объектной плоскости.

Известен ряд функций, инвариантных к преобразованию Фурье в бесконечных пределах. Например, в [14] рассматривается способ синтеза объектов, инвариантных к преобразованию Фурье путем композиции исходной функции и ее Фурье-образа. Однако при введении диафрагмы свойство Фурье-инвариантности таких объектов нарушается. Более удобными для диафрагмирования являются функции Гаусса-Эрмита и Гаусса-Лагерра, энергия которых как в объектной, так и частотной плоскостях сконцентрирована на ограниченном отрезке. Хотя, строго говоря, эти функции инвариантны к преобразованию Фурье в бесконечных пределах.

В [15] были использованы функции Гаусса-Эрмита (ФГЭ) как начальное приближение в итерационном расчете ВСВФ нулевого порядка:

g n ^{( x} ) = exp

(    2 I

H

l 2U 7

^^^^^^B

" I x I n I I , laJ

пространение световых полей в свободном пространстве описывается преобразованием Френеля:

где H_n ( x ) - многочлен Эрмита, с - радиус гауссового „ -12 пучка, с = c   .

В данной работе расчет одномерных ВСВФ проводился на основе алгоритма, описанного в работах [16, 17].

На рис. 1, 2 показаны графики ФГЭ и ВСВФ (рис. 1а, 2а) и модулей их Фурье-образов (рис. 1б, 2б), полученных с помощью формулы (5), при различных значениях параметра c .

Для c =20, n =3 вся энергия y n ( x ) сконцентрирована на отрезке [ - 1,1] ( Д ,( c ) = 1,00, п₀ =12). Энергия g n ( x ) также практически вся включается в этот отрезок. На рис. 1б видно, что обе функции демонстрируют инвариантность к преобразованию Фурье: среднеквадратичное отклонение модуля спектра ФГЭ от модуля самой ФГЭ составило 5 =0,12%, а для ВСВФ отклонение определялось лишь ошибкой численного интегрирования и составило 5 =0,0001%.

exp( ikz ) х

T /2

х

Г²       х ik /        .2 ,

J f ⁽ x ^)exp —⁽ y ^- x ) d x

- T /2           ^{L             J}

.

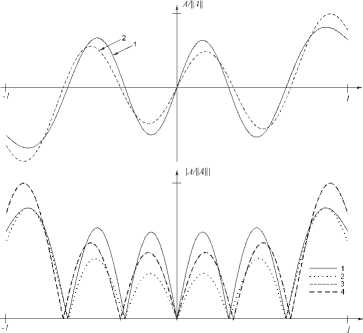
Рис. 2. Сравнение Фурье-спектров для ФГЭ и ВСВФ при n=5 , c=10, X _n (c)=0,825: (а) ФГЭ (линия 1) и ВСВФ (линия 2); (б) модули ФГЭ (линия 1) и ее Фурье-образа (линия 2), ВСВФ (линия 3) и ее Фурье-образа (линия 4).

■ -HI

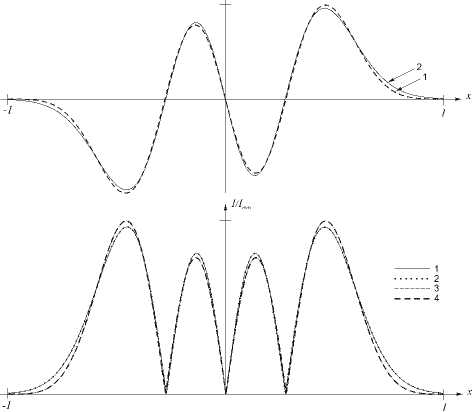
Рис. 1. Сравнение Фурье-спектров для ФГЭ и ВСВФ при п=3, c=20, X _n(c) = 1,00:

(а) ФГЭ (линия 1)

и ВСВФ (линия 2); (б) модули ФГЭ (линия 1) и ее Фурье-образа (линия 2), ВСВФ (линия 3) и ее Фурье-образа (линия 4).

Для c =10, n =5 за отрезком [ - 1,1] находится менее 18% энергии y n ( x ) ( Д ,( c )=0,825, n₀ =6), аналогично и для g n ( x ). Однако на рис. 2б видно существенное нарушение свойства Фурье-инвариантности для ФГЭ ( 5 =28,24%) и его сохранение для ВСВФ ( 5 =1,02%).

Двумерные ВСВФ нулевого порядка могут быть получены как произведение одномерных y _nm ( x , y ) = y _n ( x ) ■ y _m ( y ). На рис. 3 показана двумерная ВСВФ (3,5) для c =10 (а) и c =7 (б) и их Фурье-образы (соответственно рис. 3в и 3г).

В [8] было сделано предположение, что ВСВФ обладают также свойством самовоспроизведения при распространении в пространстве. Параксиальное рас-

а

в                         г

Рис. 3. Двумерная ВСВФ (3,5) для c =10 (а) и c =7 (б) и их Фурье-образы, (в) и (г), соответственно.

На рис. 4, 5 показаны графики ВСВФ и модулей их Френель-образов, полученных с помощью формулы (12), при различных значениях параметра c . Видно, что y n ( x ), собственные числа Д , которых практически равны единице (то есть на отрезке [ - T /2, T /2] заключена вся энергия), примерно сохраняет свой вид (с точностью до масштаба) на всей оптической оси (рис. 4). Если же Д , <1, то y n ( x ) в зоне дифракции Френеля претерпевает значительные изменения, затем с ростом расстояния z посте-

пенно восстанавливается и самовоспроизводится в зоне дифракции Фраунгофера (рис. 5).

Н.МН

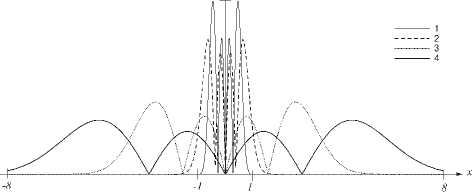
Рис. 4. Распространение ВСВФ при n=3 , c =20, X _n (c) = 1.00 в свободном пространстве: модули при z =0 (линия 1), z=500мм (линия 2), z=2 750мм (линия 3), z=5000 мм (линия 4).

f ( x ) = Е f n V n ( x ), n = 0

где

1 T /2

f n =       J f ^{( x} ) V n ^{( x )d} X .                  ⁽¹⁴⁾

^Л n — t /2

В [7] показано, что существенными являются первые M < n₀ членов ряда (14). Именно n₀ =2 с/ п =2 Tw₀ определяет число Шеннона для ВСВФ [3]. Кроме того, при вычислении коэффициентов (14) для n > n₀ будет происходить деление на A n « 0, что может вносить существенные ошибки. Поэтому будем далее рассматривать некоторую аппроксимацию заданного светового поля:

мни

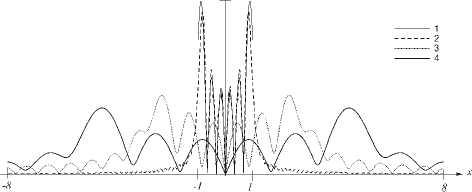
Рис. 5. Распространение ВСВФ при n=5 , c=10, X _n (c)=0,825 в свободном пространстве: модули при z=0 (линия 1), z=500 мм (линия 2), z=2750 мм (линия 3), z=5000 мм (линия 4).

M

f ^{( x} ) = Е f n V n ^{( x} )• n = 0

Заметим, что выражение (2) можно рассматривать как коэффициенты (14) ряда (13) для функции:

sin

2 c, ч у ( У ^{- x} )

п ( у - x )

да

= Е a n ⁽ у ^{y (} x ) = n = 0

да

= Е ^А п У п ⁽ У > n ^{( x} ) n = 0

На рис. 6 показаны графики среднеквадратичного отклонения модулей Френель-образов от модулей исходных ВСВФ для различных значений собственных чисел. Видно, что для y n ( x ) с A n = 1 отклонения значительно ниже, и самовоспроизведение наступает гораздо раньше, чем для y _n ( x ) с A n <1.

sin x

Т. к. lim----- = 1, то x —>0 x

да

—  Е^Л n V ² ( x ).                      (17)

^{п T} n = 0

и пользуясь свойством ортогональности (8), получаем:

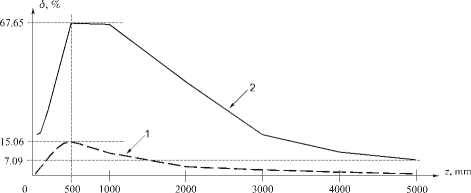
Рис. 6. Среднеквадратичное отклонение при распространении ВСВФ при n=3 , c=20,

X _n (c) = 1,00 (линия 1) и при n=5, c=10, X _n (c)=0,825 (линия 2) в свободном пространстве в зависимости от расстояния z.

T /2 да                   да     T /2

J Е ^A n Wn ⁽. ^{x )d x} = Е ^A n J y 2 ^{( x )d x} =

- T /2 n = 0               n = 0 - T /2

да

= Е An = - = n о

= n

Благодаря свойству (7) изображение, согласованное с ВСВФ, будет обладать модовым характером при прохождении через оптические линзовые системы с ограниченной апертурой. То есть, такое изображение будет устойчиво к дифракционным эффектам, связанным с ограниченными размерами апертуры оптической системы.

ВСВФ представляют собой полный набор ортогональных функций с ограниченной спектральной полосой. Таким образом, бесконечным рядом по ВСВФ можно представить любое световое поле:

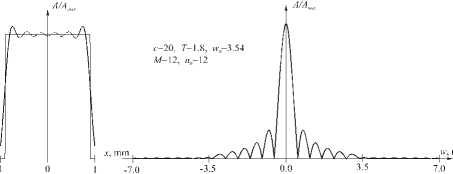
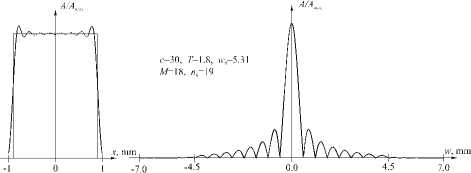
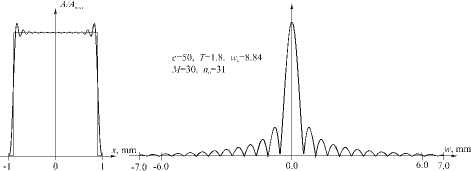
Чтобы повысить точность аппроксимации (15), нужно увеличивать значение параметра c , так как n₀ =2 с/ п . На рис. 7 показаны аппроксимации прямоугольника ВСВФ для различных значений параметра с и Фурье-спектры этих аппроксимаций. Видно, что ростом параметра c точность аппроксимации повышается: 5 =14,98% (рис. 7а), 5 =13,46% (рис. 7в), 5 =11,88% (рис. 7д). Однако за это приходится платить расширением спектра (сравни рис. 7б, г, е). Если ряд (15) содержит только y n ( x ) с собственными числами, практически равными 1 (то есть A m = 1), то спектр изображения f ( x ) будет находиться внутри отрезка [ - w₀, w₀ ], w₀ = c / T n . Если же A _M <1, то спектр выйдет за этот отрезок. Так как A ₁₂ (20)=0,588, A ₁₈ (30)=0,707, A ₃₀ (50)=0,865, то нет гарантии, что спектры полученных аппроксимаций не выйдут за частоту w 0 .

а                     б

за исключением некоторых точек, лежит ниже линии 2. То есть ВСВФ обеспечивают меньшие искажения для изображающих систем с ограниченным зрачком, чем ФГЭ.

в                          г

д                       е

Рис. 7. Аппроксимации прямоугольника ВСВФ для различных значений параметра с (а, в, д) и соответствующие им модули спектров (б, г, е).

•1         О         I-]         о а                     б

О                              I               -I                             О в                          г

д                       е

Однако при соблюдении условия M ≤ n 0 , количество энергии в спектре за отрезком [ - w 0 , w 0 ] будет немного, и потери информации при таком диафрагмировании будут невелики. На рис. 8 приведены результаты моделирования прохождения сигнала через линзовую систему с ограниченным зрачком.

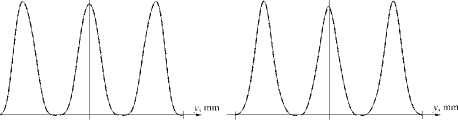
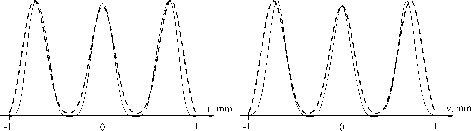
При моделировании рассматривалась аппроксимация косинусного сигнала f ^€( x ) рядом (15) по ВСВФ и, для сравнения, по ФГЭ. При M =16, c =30 среднеквадратичная ошибка аппроксимации составила δ =7,19% для ВСВФ и δ =11,29% для ФГЭ (рис. 8а и 8б соответственно линия 1 - исходный сигнал, линия 2 - аппроксимация). На рис. 8ж показаны графики модулей спектров каждой из аппроксимаций: линия 1 - для ВСВФ, линия 2 - для ФГЭ. Далее спектры подвергались усечению до частоты w c .

Учитывая, что λ ₁₆ (30)=0,985, усечение до частоты w c =5 ( w 0 =5,31) не должно привести к потере информации в изображении. Действительно, в этом случае среднеквадратичное отклонение интенсивности изображения от интенсивности аппроксимации составило δ =0,02% для ВСВФ (рис. 8в) и δ =0,93% для ФГЭ (рис. 8г). При уменьшении размеров диафрагмы ошибка будет расти. Так, при усечении спектра до частоты w_c =1,5 отклонение составило δ =24,17% для ВСВФ (рис. 8д) и δ =34,67% для ФГЭ (рис. 8е).

На рис. 9 приведены графики среднеквадратичного отклонения интенсивности изображения от интенсивности аппроксимации косинусного сигнала по ВСВФ (линия 1) и по ФГЭ (линия 2) в зависимости от частоты усечения спектра w c . Видно, линия 1,

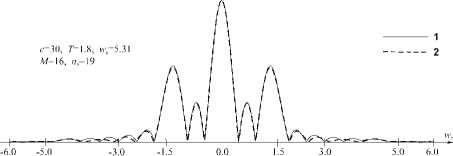
Рис. 8. Аппроксимации косинусной функции рядом (16) по ВСВФ (а) и по ФГЭ (б) при M=16, c=30, и восстановление этих аппроксимаций по спектру (ж), усеченному до частоты w _c =5 (в, г) и w _c =1,5 (д, е).

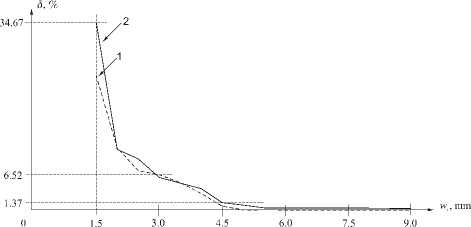
Рис. 9. Ошибка изображения при аппроксимации косинусной функции рядом (15) по ВСВФ (линия 1) и по ФГЭ (линия 2) в зависимости от частоты усечения спектра w c .

На рис. 10 приведены графики эффективности, то есть количества энергии, сохранившейся в изображении, при прохождении через линзовую систему аппроксимации косинусного сигнала по ВСВФ (линия 1) и по ФГЭ (линия 2) в зависимости от ширины диафрагмы 2 w c в частотной плоскости. Видно, что линия 1 практически достигает 100% на частоте

w_c =4,5 и лежит выше линии 2 вплоть до частоты w_c =3,3.

Таким образом, на основании рис. 9 и 10 можно говорить, скорее, о выигрыше ВСВФ, по сравнению с ФГЭ в смысле меньших искажений сигнала, чем энергетических потерь.

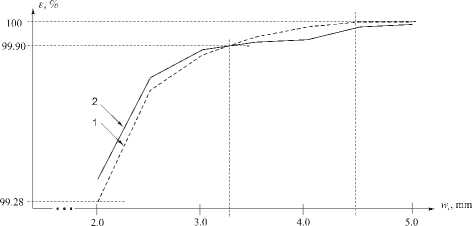
Рис. 10. Эффективность изображения при аппроксимации косинусной функции рядом (15)

по ВСВФ (линия 1) и по ФГЭ (линия 2) в зависимости от частоты усечения спектра w c .

Заключение

В данной работе получены следующие результаты.

На численных примерах подтверждена устойчивость дифракционной картины Фраунгофера вытянутых сфероидальных волновых функций нулевого порядка к введению диафрагмы в объектной плоскости. Для сравнения показано, что при экранировании части энергии функций Гаусса-Эрмита их свойство Фурье-инвариантности нарушается.

На численных примерах показано самовоспроизведение сфероидальных функций на некотором расстоянии при распространении в свободном пространстве. При этом, чем собственные числа λ n ближе к единице, тем раньше наступает самовоспроизведение.

Проведено численное моделирование прохождения сигнала, согласованного со сфероидальными функциями и, для сравнения, с функциями Гаусса-Эрмита, через линзовую систему с ограниченным зрачком. Исследование влияния размеров диафрагмы в спектральной плоскости на точность и эффективность передачи изображения показало, что выигрыш сфероидальных функций, по сравнению с функциями Гаусса-Эрмита достигается, скорее, в смысле меньших искажений сигнала, чем энергетических потерь.

Работа поддержана Российским фондом фундаментальных исследований (гранты 00-15-96114, 00-01-00031).