Влияние динамических параметров нагружения при вибротрении на эквивалентные напряжения и скорость износа в скользящем контакте

Среди многочисленных факторов влияния на интенсивность фреттинг-износа металлов и сплавов наибольшее влияние оказывают параметры внешних механических воздействий: контактное давление, амплитуда и частота осцилляций на контакте. Обобщение результатов исследований отечественных и зарубежных авторов [1] показало, что определение роли перечисленных факторов в механизме разрушения контактирующих при фреттинге поверхностей не завершено.

Накопленный к настоящему времени обширный теоретический и экспериментальный материал в области механики контактных взаимодействий [1, 2] позволяет проводить расчеты фактической площади контакта (ФПК), объема вовлеченного в контактную деформацию материала, напряжений и других характеристик структуры ФПК номинально неподвижных шероховатых поверхностей при различных видах деформации микронеровностей: упругой, пластической, упруго-пластической. Установленные расчетные зависимости не учитывают влияния скорости скольжения в контакте, что сдерживает распространение их на случаи расчета эквивалентных напряжений и скорости износа при совместном действии нормальных и тангенциальных сил на вовлеченный в контактную деформацию микрообъем материала.

предложенной автором [3, 4] обобщенной кинетической термофлуктуационной модели изна- шивания при трении:

„ z.CkT Л

Vh =---exp a h apAa

£»C ^_ ^экв" ct        Up kT

или в условиях ведущей роли «атермического» механизма износа при аэкв/ар ^ 1

,

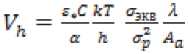
где ^h – скорость линейного износа, м/с ; ^s= 0,1 0,2 – относительное удлинение, при котором межатомная связь теряет устойчивость и разры- вается; С – атомная (молярная) теплоемкость, Дж/°К, для одноатомных кристаллов С 3k, где k =1,38×10-23, Дж/°К – постоянная Больцмана; a - коэффициент термического линейного расширения, °K ; h= 6,626×10-34 Дж/Гц – постоянная Планка; Т – термодинамическая температура, °К; ^£E – номинальная площадь поверхности трения, м2; l - число фрикционных связей (опорных точек) на поверхности трения; Dp- разрывное напряжение, H/м2; sэкв – эквивалентное напряжение на поверхности скользящего контакта, Н/м2.

РАСЧЕТ НАПРЯЖЕНИЙ В ПЛОСКОМ СКОЛЬЗЯЩЕМ КОНТАКТЕ

При сближении под действием нормальной нагрузки двух шероховатых поверхностей формируется ФПК, равная сумме элементарных площадок контакта, возникающих при деформации отдельных микронеровностей. В прилегающей к ФПК области при взаимном внедрении шероховатостей в поверхности двух тел образуется некоторый микрообъем материала, который вовлекается в контактную деформацию. Среднее касательное напряжение на ФПК найдем, определив полную механическую энергию сдвига этого микрообъема, при следующих допущениях: весь внедренный микрообъем материала деформируется одновременно; сдвиг микрообъема происходит в плоскости, параллельной плоскости трения; деформация осуществляется в области упругости и на границе упругости, при достижении текучести материала рост нагрузки не вызывает значительных изменений напряжения; увеличением ФПК при сдвиге пренебрегаем. Последнее связано с тем, что даже при пластическом контакте приложение тангенциальных сил к сопряжению приводит к увеличению ФПК не более чем на 5% [2].

Пусть элементарный микрообъем (рис. 1) в виде кубика находится в условиях сдвига [6]. Величина сдвига грани CD равна СС₁= DD₁ = Угол сдвига - Так как упругие деформации и деформации в области перехода к текучести материала малы, то можно принять

(3) где a – расстояние между гранями кубика.

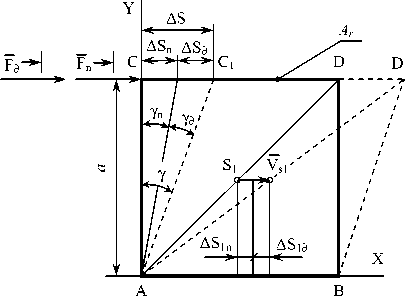
Рис. 1. Иллюстрация сдвига

Обозначим площадь грани, по которой действуют касательные напряжения, Ar, а усилие, действующее вдоль этой грани, представим, используя принцип независимости действия сил, двумя векторами       .Усилие – квазиста- тическое, постепенно возрастая от нуля до конечного значения вызывает сдвиг на величину

. Усилие – динамическое, под действием которого общий центр масс выделенного элемента на участке перемещения приобретает скорость , а грань CD сдвигается на величину . Из геометрических соображений (рис. 1) получим:

, (4) где

,.(5)

Касательные напряжения сдвига определятся [6] как

,, где G – модуль сдвига.

С другой стороны

=          ,/

Решая совместно (5), (6), (7), получим:

=             ;( 8)

Полная механическая энергия сдвига

W =(9)

Потенциальную энергию сдвига представим как работу силы на пути перемещения

. Эта работа выражается [6] площадью треугольника (рис. 1)

Подставляя в (10) из равенства (8), получим

.

Умножив и поделив выражение (11) на величину площади грани, по которой действуют касательные напряжения и, приняв во внимание (7), найдем значение потенциальной энер- гии сдвига в виде:

= G ,(12)

где          – вовлеченный в контактную де формацию микрообъем материала, а напряжение

Кинетическая энергия сдвига определится из выражения

/2,(14)

где m – масса деформируемого объема материала,             –скорость деформации.

Полагая              , получим

, или                 , (15)

где V =    t – скорость сдвига в плоскости трения.

Подставляя в уравнение (15) из равенства (8), найдем д$а ..    |_=1 г- ■■ но , а           , где - ускорение, тогда

Умножив получим

и поделив выражение (17) на

,(18)

а напряжение

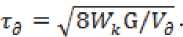
Складывая (13) и (19), получим полное каса- тельное напряжение при сдвиге

Подставляя в уравнение (20) выражения (10) и (15) потенциальной и кинетической энергии сдвига, найд ем

Положив в выражении (21) m= где -плотность материала;  = N, где N – нормаль ная нагрузка, – коэффициент трения; значение из равенства (8) и сделав некоторые преобразования, получим выражение для касательного напряжения в виде:

, (22)

где q_r = N/Ar – фактическое нормальное давление в контакте.

В условиях возвратно-поступательного или вибрационного трения максимальная скорость скольжения V 2тгД1 , где А – амплитуда, f – частота осцилляции в контакте, а напряжение сдвига t = qrp, +2лА^ГрС. (23)

Из анализа напряженного состояния материала на скользящем контакте авторы работы [2] установили, что эквивалентное напряжение определится как

°™ = ^ , (24) где Ki – коэффициент, зависящий от принятой гипотезы прочности. При использовании гипотезы наибольших нормальных или касательных напряжений Ki =3, а эквивалентное напряжение в области фактического контакта определится как

^ЭКЕ =3T = 3(q_r/i +2 тгА^ГрС ). (25)

Выражения (22) и (23) предсказывают линейную зависимость касательного напряжения от нагрузки и скорости (амплитуды и частоты) относительного проскальзывания в контакте.

Зависимость влияния каждого из слагаемых формулы (23) оценим расчетным путем в условиях вибрационного трения (фреттинга) одноименной контактной пары из сплава ВТ9 при следующих данных: N=300 Н, Ar= 0,357■ 10-6 m2 , Ц = 0,54, p = 4480 J, G = 0,38 ■ E, где Е= 1,1■ ЮиН/м - модуль упругости материала, А = 15■ 10”6m, f = 310 Гц, т = (454 ■ 106 + 0,4 ■ 106) Д/м2. (26)

Как следует из расчета, такая модель дает качественно правильное представление о связи напряжения с параметрами динамического нагружения. При умеренных скоростях скольжения (амплитуде и частоте) вторым слагаемым в выражениях (22) и (23) можно пренебречь вследствие его малости (1%) по сравнению с первым слагаемым. При высоких и сверхвысоких скоростях скольжения влияние второго слагаемого может стать заметным, что проявлялось в росте скорости изнашивания [1, 2], при одновременном снижении коэффициента трения.

Как показала практика оценки скорости износа образцов при лабораторных, стендовых испытаниях и в условиях эксплуатации [4,5] при малых и средних нагрузках пластическая деформация (течение материала) возникает на вершинах микронеровностей, а среднее фактическое давление на контакте достигает q_r = ^^lff_T, где °T – напряжение текучести материала. При увеличении внедрения микронеровностей с повышением фактического давления пластическая деформация распространяется на весь контакт, а qr = ", , где c = 3 по А.Ю. Ишлинскому [2].

При многократном возвратно-поступатель- ном взаимодействии микронеровностей наблюдается тенденция к вырождению пластического контакта в упругий. Фактическое нормальное давление на контакте, соответствующее переходу от пластического к упругому деформированию, определится по зависимости И.А. Вяткина [2]

q_r = °r/^ki^ ,            (27)

где величина k±, уточнённая Е.Ф. Непомнящим, определяется по формуле

^Ki=1,5 /₄(1-д₀_д²) + ^^ ,  (28)

где /^0 – коэффициент Пуассона.

Расчет скорости износа различных металлов и сплавов с учетом выражений (27 и 28), то есть в предположении упруго-пластического контакта при фреттинге, показал хорошее приближение расчетных и экспериментальных данных [4, 5].

МЕТОДИКА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ

Лабораторные испытания с целью исследования влияния факторов динамического нагружения (нагрузки, частоты и амплитуды колебаний) на скорость износа образцов из титанового сплава ВТ9 в условиях фреттинга проводились на специально разработанном стенде [4, 5], позволяющем варьировать рабочие параметры нагружения в условиях многокомпонентной вибрации. Испытывались плоские пары одноименных образцов по двухопорной схеме [5] c общей номинальной площадью контакта 30 мм². Рабочие поверхности образцов изготавливались фрезерованием и притиркой на плите с алмазной пастой до получения шероховатости ^G - 0,4…0,8 мкм по ГОСТ 2789-73. Нормальное нагружение в контакте осуществлялось грузом, действующим через систему рычагов и гибкую тягу на верхний подвижный образец.

Осцилирующие движения подвижного образца в горизонтальной плоскости, в двух взаимно-перпендикулярных направлениях, и пульсирующая нормальная нагрузка в контакте создавались тремя вибраторами электродинамического типа (ВЭД), мощность каждого из которых 200 Вт и тяговое усилие – 200 H. Возбуждение ВЭД осуществлялось генератором ГЗ-34 и усилителем ТУ-600.Частота контролировалась частотомером-хронометром Ф5080. Амплитуды колебаний в двух взаимно-перпендикулярных направлениях измерялись датчиками емкостного типа в комплекте с виброизмерительным прибором ВВ–IOH.

Параметры внешних воздействий при испытаниях изменялись в следующих пределах: частота колебаний – 30…310 Гц; среднегеометрическая амплитуда 3,5…30 мкм, при которой на контакте реализуются присущие фреттингу процессы [1]; контактное давление 1…15 МПа; объемная температура – 293

Испытания проводились при одно- или многокомпонентной вибрации без смазки, с возбуждением колебаний вибраторов в одной фазе.

Переменную составляющую контактного давления в стыке задавали в виде периодической функции                     а результирую щее нормальное давление определяли как сумму q=                                (29)

где   = (1.0…11) МПа – диапазон значений ста тистического давления, создаваемого весом груза;        (3,0…5,0) МПа – диапазон значений переменной составляющей давления в контакте.

Величину износа неподвижного образца (контробразца) определяли как среднюю арифметическую величин линейных износов дорожки трения, профиль которой записывался профилографом-профилометром ВИ-201.

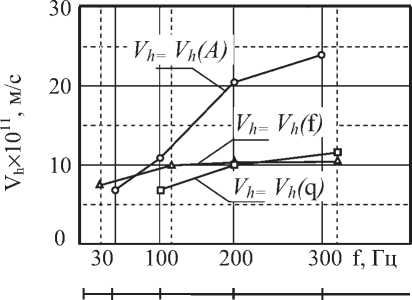
Результаты исследования влияния параметров динамического нагружения (нагрузки, частоты и амплитуды колебаний) на скорость износа сплава ВТ9 приведены на рис. 2.

7 15     30      45

A x lO³, мм

I-------------------------------------1-----------------------------------1--------------------------------------------1--------------------------------------

3      7        11

q _cm , МПа

Рис. 2. Зависимость скорости линейного износа сплава ВТ9:

• (A) – от амплитуды

();

– от давления (A = 0,015 мм,);

• (f) – от частоты (A=0,015 мм,);

= 3 МПа, Т=293°K

Установленная функциональная связь напряжения с параметрами динамического нагружения (23, 26) в условиях фреттинга сплава ВТ9 подтверждается экспериментально (рис.2) через скорость износа, пропорциональную действующим на контакте напряжениям. Скорость линейного износа сплава в установившемся режиме фреттинга слабо возрастает с ростом частоты (скорости) осцилляции, более интенсивно с ростом нормального давления. Влияние амплитуды осцилляции неоднозначно. Увеличение амплитуды приводит к росту скорости относительно проскальзывания, перекрытия на пятнах фактического контакта, активируемого объема материала, увеличению пути трения и смене характера контактного взаимодействия (от номинально неподвижного при фреттинге до трения скольжения) и изнашивания [1], что, очевидно, и ведет к резкому повышению скорости линейного износа.

ЗАКЛЮЧЕНИЕ

Установлена математическая связь и оценен уровень влияния параметров внешних механических воздействий при вибрационном трении (фреттинге) на величину эквивалентных напряжений на площадках фактического контакта при одновременном действии нормальных и касательных напряжений. Экспериментально исследовано влияние внешних факторов динамического нагружения (нагрузки, частоты и амплитуды колебаний) на скорость линейного износа поверхностей трения образцов из титанового сплава ВТ9. Установленная математически функциональная связь напряжения с параметрами динамического нагружения подтверждена экспериментально через скорость линейного износа, пропорциональную действующим в скользящем контакте напряжениям, что подтверждает правомерность использования выражения для расчета эквивалентного напряжения в расчетной термофлуктуационной модели скорости изнашивания.