Влияние динамики включения на распространение упругих волн в акустическом волноводе

Исследованию вопросов распространения звуковых волн в бесконечном акустическом волноводе посвящено огромное количество работ. Особое место среди рассматриваемых проблем занимают задачи, в которых волновод имеет изменяющийся профиль сечения. Данный класс задач вызывает повышенный интерес, так как в зоне изменения сечения происходит перестроение фронта волны, что, в свою очередь, порождает ряд интересных эффектов, одному из которых посвящена данная работа.

Рассматривается акустический волновод с включением (Рис. 1). На практике в роли волновода могут выступать системы трубопроводов, а в качестве включения — различного рода отложения на внутренней поверхности трубопровода. Так, при использовании газопроводов, лежащих на дне моря, в условиях пониженных температур и большого давления на стенках трубы могут образовываться гидраты, что приводит к снижению пропускной способности, а иногда и к полной закупорке газопровода [1]. Выявление местоположения, а также геометрических размеров отложения усложняется тем, что трубопроводы, как правило, имеют большую протяженность и поэтому пошаговое «простукивание» нельзя признать эффективным [2]. В связи с этим широкое применение получили методы акустического исследования. Основная идея этих методов заключается

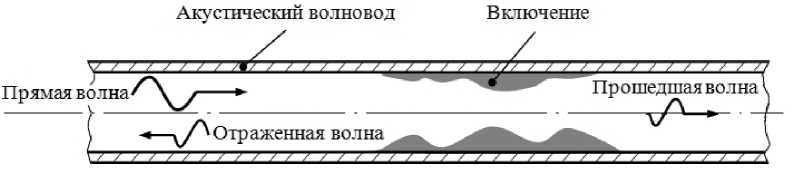
Рис. 1. Схема проведения исследований в акустическом волноводе, имеющем включения в том, что в трубу помещается излучатель, который генерирует акустические волны. При прохождении прямой волны через отложение образуются отраженная и прошедшая волны. Эти волны, фиксируемые приемниками, анализируются, и делаются выводы о параметрах включения.

Практические вопросы и теоретические исследования возбуждения и прохождения акустической волны в трубе, заполненной и окруженной жидкостью, достаточно полно рассмотрены в работах [3–11]. Наличие в трубе включения вносит в задачу свою специфику. Так, в [12] обсуждается ставшая классической постановка задачи прохождения волны в прямоугольном волноводе с преградой, имеющей щель, и показано влияние размеров щели на получающуюся волновую картину. Исследования последних лет направлены на изучение прохождения торсионных мод в трубе с включением [2, 13, 14]. Эти моды для трубы без включения имеют такие частоты отсечек, ниже которых спектр пуст. Внесение в трубу включения приводит к смещению данных частот, которое определяется радиальными размерами включения. Однако за кадром остается влияние акустической среды, заполняющей и окружающей трубу.

Повышение степени адекватности математических моделей реальным условиям эксплуатации трубопроводов сопровождается, как правило, уточнением количественных характеристик эффектов, установленных с помощью упрощенных моделей, и возможным появлением новых эффектов. В связи с этим представляется целесообразным последовательное усложнение моделей, а иногда — возвращение на нулевой уровень, чтобы увидеть эффект в «чистом» виде.

Методы решения нестационарной задачи распространения звуковых волн, вызываемых некоторыми динамическими источниками в акустическом волноводе с включением, можно условно разделить на аналитические и численные.

Аналитическое решение можно строить двумя путями. Первый путь –– это непосредственное вычисление и суммирование волн: прямой, распространяющейся от места приложения нагрузки, и волн, отраженных от границ тела; второй –– представление решения в виде суммы (ряда, интеграла) некоторых стационарных состояний тела (свободных колебаний) [15]. И тот, и другой путь позволяет рассматривать узкий класс задач со значительными ограничениями, накладываемыми на форму включения.

В отличие от аналитических, численные методы (в первую очередь метод конечных элементов) не имеют подобных ограничений и позволяют описывать произвольную форму включения. С другой стороны, проведение анализа численных результатов без выявления тех или иных особенностей на уровне простых аналитических моделей вряд ли представляется доказательным.

В связи с этим статья разбита на две части. В первой части рассматривается модель бесконечного стержня с инерционно-упругим включением в виде грузика на двух пружинах. Выбор такой модели интуитивно понятен. Действительно, простейшей моделью акустического волновода при распространении нулевой осесимметричной моды, является стержень, работающий на растяжение–сжатие, а область включения (само включение плюс жидкость, заключенная внутри него) можно представить как некий объект, обладающий своими инерционно-упругими характеристиками, например, как грузик на пружине. Данная модель показывает, что на частоте, близкой к парциальной (собственной) частоте грузика, амплитуда отраженной волны равна нулю, в то время как амплитуда прошедшей волны достигает своего максимума. То есть параметры включения, а именно парциальная частота, определяют характер отраженной и прошедшей волн. Данные выводы перенесены во вторую часть статьи, в которой исследуется прохождение нулевой осесимметричной моды в круглой трубе с абсолютно жестким включением цилиндрической формы.

• 2.    Бесконечный стержень с инерционно-упругим включением

Рассмотрим бесконечный стержень с площадью поперечного сечения F , модулем Юнга E и плотностью р , который при x = 0 (ось х направлена вдоль оси стержня) имеет включение в виде грузика массой m , соединенного со стержнем посредством двух пружин с жесткостью c (Рис. 2). В качестве возмущения выступает волна, приходящая по левой части стержня из бесконечности.

Рис. 2. Схема бесконечного стержня с инерционно-упругим включением

Обозначим через у смещение грузика вдоль оси х , тогда уравнение динамического равновесия для него запишется как

my = - 2 су + ^cu1 x = ₀ + ^cu 21 x = ₀

где u 1 ( x , t ) и u ₂ ( x , t ) — продольные смещения поперечных сечений левой и правой частей стержня соответственно; точка обозначает дифференцирование по времени. Уравнения продольных колебаний обеих частей стержня имеют вид:

д ² u,    1 д ² u,

—т---z--Л = 0

д x ²    c l д t²

i = 1,2 ,

где c l = ^ El р — скорость звука в стержне; нижний индекс i обозначают левую ( i = 1) и правую ( i = 2) части стержня соответственно. Граничные условия определяют

сопряжение торцов обеих частей стержня с пружинами:

^EF        =— ^c ' ^U 1 x - ° - y ) ;

^д x x - 0

дu

EF дx x=0

= c (u 2| x=0 - У ) .

Примем, что в начальный момент времени

y t = 0 = 0,      y t = 0 = 0,     u t = 0 = ^u 0 ^{( х} ) ,        ^u 2 L= 0 = 0,                                    ⁽⁵⁾

где u ₀ ( х ) — произвольная функция, такая, что u ₀ ( 0 ) = 0 . Решения уравнений (2) представим в форме д'Аламбера [16]:

u i = ф i ( tc l - x ) + v i ( tc l + x ) i = 1,2.                                                       (6)

В этой формуле первое слагаемое соответствует волне, распространяющейся в положительном направлении оси x , а второе — в отрицательном. Исходя из физического смысла слагаемых, находим: ф 1 ( tc l - x ) = u 0 ( tc l - x ) и y ₂ ( tc + x ) = 0. С учетом этого запишем выражения (6): u 1 = u ₀ ( tc l - x ) + у 1 ( tc l + x ) и u 2 = ф ₂ ( tc l - x ) . Тогда динамическое уравнение равновесия для грузика (1) примет вид:

my = - 2 cy + c ( u о ( tc, ) + V i ( tc , ) ) + c Ф 2 ( tc , ) . (7)

Найдем производные перемещений:

5 u.        1 .      1 . du2

=--u 0 + —V1,          2 = оx     cl cl              оxc

Введя обозначения й₀ = u ₀ | x = 0 , Й 1 = Й 1 | _x = ₀ , ф ₂ =ф ₂ | _x = ₀ и приняв во внимание (8),

EF ( - й_й cc + + Й 1 /c l ) = - c ( й 0 + Й 1 ) + cy ,

перепишем граничные условия (3) и (4):

- EF ф ₂ / c l = c ф ₂ - cy . Отсюда

-cy + c(i?0 + Й 1) = EF(^0 -Й1)/c,

- cy + cф 2 = - EF ф 2 /cl.

Вернемся к динамическому уравнению равновесия для грузика (7). В новых обозначениях оно перепишется в виде

my = -2cy + c (u0 + Й1) + cф2.

Подставив сюда (9), получим:

уравнение по времени, найдем my

EF z

my =--- u 0 c_l

• •

EF EF

---Й 1-- ф ₂ . Проинтегрировав это

cl

EF

cl

EF

---ф₂ + Const. В силу начальных c_l

EF

zf

=--- ^u 0-- Й 1

cl

cl

условий (5) Const = 0. Тогда

Й 1 +ф 2

= ^u 0

mc l y. EF

•

Подставив (11) в (10), получим my =- 2 cy + cH₀ + c ( й₀ - ( mc l y )/( EF ) ) или my + ( mccy )/( EF ) + 2 cy = 2 cH₀. Разделив данное уравнение на m и введя обозначения 2 n = c l c /( EF ) и to ₀ = 2 c/m , придем к виду: y + 2 ny + ю 0 y = м 2 й₀ .

Таким образом, для смещения грузика получилось стандартное уравнение вынужденных колебаний осциллятора с вязким трением. Эффект возникновения трения в системе из идеальных элементов за счет ухода энергии на бесконечность на примере осциллятора на упругом волноводе впервые был получен в работе [17]. Однако в данной работе более интересными представляются отраженная Й 1 и прошедшая ф ₂ волны.

Для анализа этих волн рассмотрим случай, когда на левую часть стержня из бесконечности приходит синусоидальная гармоническая волна, то есть й₀ = H ( t ) sin м t , где H ( t ) — функция Хэвисайда, ю — частота вынуждающего воздействия. Тогда

y + 2 ny + м ₀ y = м ₀ sin м t .

Рассмотрим установившийся режим колебаний. Частное решение уравнения (12) имеет

вид у=B(to)sin(tot+a), где B(to) = 1

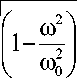
4 n ² to ²

⁺ „2 „2 ^to 0 ^to 0

sin a=- 2 n

to

1— ~2 ton

4 n ² to ²

+ „ 2 ,.2

^to 0 ^to 0

Для определения ф2 воспользуемся вторым уравнением (9), которое перепишем в виде EFф2 /(ccl) +ф2 = у, подставим у и учтем, что clc/(EF) = 2n . Тогда ф 2 /(2 n) + ср 2 = B (to) sin (tot + a). Общее решение однородного уравнения пропорционально e 2nt, то есть колебания затухают с течением времени по экспоненциальному закону. Здесь это решение не рассматривается, так как интерес представляет установившийся процесс колебаний. Частное же решение имеет вид ф 2 = С (to) sin (tot + a+p), где

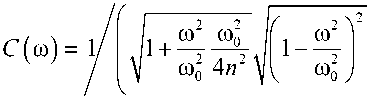
A 4 n ² to ^{2 +} „ 2 .2 ^to 0 ^to 0 7

Для определения     ф 1

,

sin p = - to/

2n to0

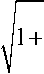
to ² to 0 to 0 4 n²

воспользуемся равенством (11), откуда

ф 1 = U0 - mcy] E -р 2 = D (to) sin (tot -£), где

D (to)=

[ cos ^ =

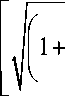
2     2

to to ₀

0 ,2 4 n

v

to

too 7

4 n ² to ²

^to 0 ^to 0

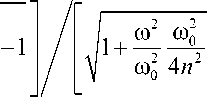
^    to ² A ²    4 n ² to ²

1--2 + —

V     ^to 0 7      ^to 0 ^to 0

X

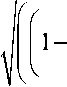
to__to^      to_ _4 n_

1 л 1     1      22

to0 4n 7v to0 7

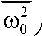
to ²

to 0

^to 2 ^to 0 to 0 4 n n

- 1 + 2 ^ ° ^to 0

to ² to 0 to 0 4 n n

X

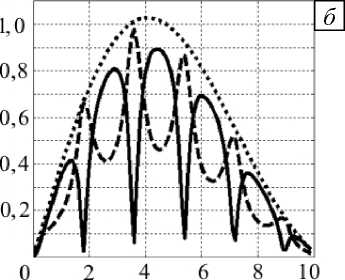
На рисунке 3 показана зависимость амплитуд колебаний грузика B ( to ), прошедшей C ( to ) и отраженной D ( to ) волн от отношения частот to/to ₀ для трех значений 2 n /to ₀ . Основной вывод из проведенного анализа следующий: на частоте, близкой к парциальной частоте колебаний грузика на двух пружинах, амплитуда отраженной волны равна нулю, в то время как проходящая волна имеет максимальную амплитуду. То есть, если через данную систему проходит акустический сигнал с полностью заполненным спектром, то спектральная плотность отраженной волны на парциальной частоте имеет минимум, а спектральная плотность прошедшей волны –– максимум. Отметим также, что смещение пиков амплитудно-частотных характеристик от значения парциальной частоты происходит вправо и определяется коэффициентом затухания n , который выражается через основные механические параметры системы.

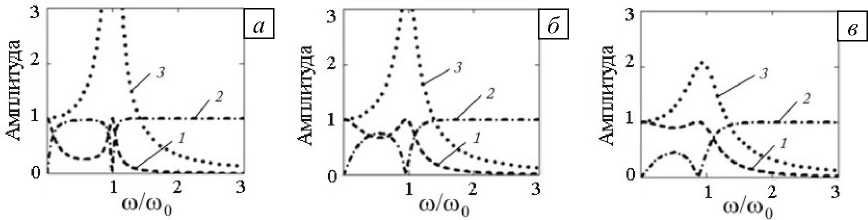
Рис. 3. Частотный отклик системы для различных значений 2 n ω₀ : 0,1 ( а ); 0,3 ( б ); 0,5 ( в );

1 – прошедшая волна, 2 –отраженная волна, 3 – грузик

• 3.    Акустический волновод с абсолютно жестким включением

Рассмотрим цилиндрическую трубу, заполненную идеальной сжимаемой жидкостью с плотностью р и упругим модулем сжатия K . Внутри трубы находится включение, представляющее собой полый цилиндр, ось которого совпадает с осью трубы (Рис. 4). Стенки трубы, как и включение, считаются абсолютно жесткими. Если провести параллель с первой частью работы, то в качестве грузика на двух пружинах выступает цилиндрический слой жидкости внутри включения.

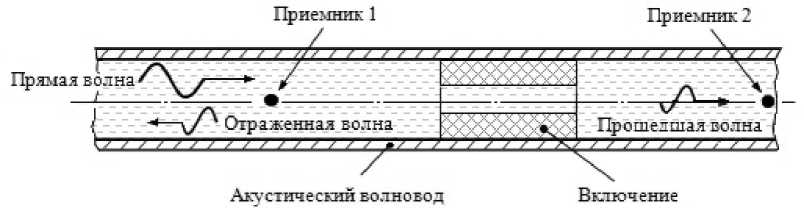
Рис. 4. Схема акустического волновода с абсолютно жестким включением цилиндрической формы

Уравнение, предназначенное для описания процесса распространения акустических волн в идеальной сжимаемой жидкости, представляет собой волновое уравнение д'Аламбера л 1 д ² p

A p -       . = 0,                                                                     ⁽¹³⁾

cf дд

где p — акустическое давление, C f = ^K /р — скорость распространения продольных волн в жидкости. Граничными условиями являются условия непроникания, то есть равенство нулю нормальной компоненты вектора перемещения на поверхностях контакта идеальной сжимаемой жидкости со стенками акустического волновода и включения. В качестве начального возмущения выступает акустическая волна, приходящая из бесконечности на левый торец трубы.

Построить в общем виде решение уравнения (13) совместно с граничными условиями поставленной задачи аналитическими методами не представляется возможным. В связи с этим в данной работе используется метод конечных элементов, реализованный в программной системе численного анализа LS-DYNA [18].

В рассматриваемой постановке торцы трубы уходят в бесконечность. Для моделирования таких границ тела применяются так называемые неотражающие граничные условия. Их формулировка, а также численная реализация достаточно подробно описаны в работах [19, 20].

Источник акустического сигнала моделируется равномерно распределенным по сечению давлением, прикладываемым к жидкости со стороны левого торца трубы.

Давление с течением времени изменяется по закону синуса в пределах одного периода, то есть

2п

Р ( t ) = Р o sin Tt ( H ( t ) - H ( t - ^T ) ) , где

p ₀ –– амплитуда, T –– период

нагружения. После окончания действия давления на левом торце ставятся неотражающие граничные условия.

При применении численных схем интегрирования необходимо задавать определенные значения параметров. В таблице 1 приведены геометрические размеры и физические постоянные для расчетной модели, а также характеристики излучаемого сигнала.

На рисунке 5 представлены результаты численного расчета — зависимости давления от времени в двух приемниках, расположенных на удалении 1 м от середины включения, а также спектральные плотности прямой, отраженной и прошедшей волн.

Таблица 1. Характеристики расчетной модели

Плотность p , кг/м3	Модуль сжатия K , ГПа	Радиус акустического волновода R 1 , м	Внутренний радиус включения R 2 , м	Длина включения l , м	Амплитуда p 0 , кПа	Период T , мс
1000	2,25	0,05	0,025	0,4	1	0,2

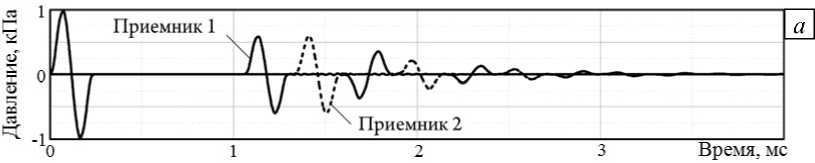
Рис. 5. Результаты численного моделирования: давление в зависимости от времени ( а ), спектральная плотность ( б );

1 – прямая волна;

2 – отраженная волна;

3 – прошедшая волна

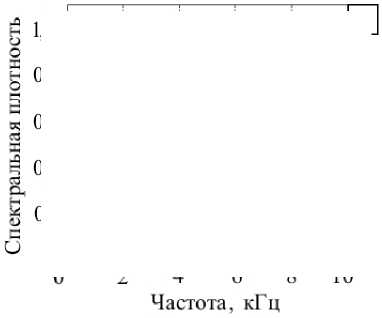
При этом приемник 1 находится перед включением, а приемник 2 –– за включением. Из графиков спектральной плотности видно, что определенные значения частот для отраженной волны оказались «вырезанными» (спектральная плотность имеет минимум). В то же время при этих же значениях частот спектральная плотность прошедшей волны имеет локальные максимумы.

Этот эффект коррелирует с результатами, приведенными в первой части работы. Там для отраженной волны оказалась «вырезанной» парциальная частота грузика на пружинах. В данном случае имеет место цилиндрический слой жидкости, находящийся внутри включения, частоты продольных колебаний которого определяются из стандартного уравнения:

5 ² u 1 5 ² u

^^^^^^^^^^^^^^^^^^^^^^^^e   ^^^^^^^*   ^^^^^^^^^^^^^^^^e ^^^^^^^^^^^^^^^^^^^^^^^^^

5 z ²    c} 5 t²

где u –– продольное перемещение сечения цилиндра при колебаниях; z –– ось круговой симметрии системы «труба-включение». В качестве граничных условий на торцах цилиндра выступает условие приложенной сосредоточенной массы, величина которой в рассматриваемом случае определяется выражением присоединенной массы [21]:

p ( n R 2 ) 2                                                                                      -1

––

M =        2^—-, где F ( RR ) = ( 1 - 1,4093 R R + 0,3 3 82 R³ R^ ³ + 0,0679 R⁵ R^ ⁵ + ... )

4 R 2 f ( RJR 2 )           ^{v     27 x                                                    7}

функция Фока.

Таким образом, если решение уравнения (14) ищется методом Фурье, то получается следующее частотное уравнение:

K (nR2) cf

to M to ² cos— +— ^2 ^ sin —

^^^^™

c f c

c

(           K (ЛR2)

M to ² M to ² sin ^{to l} --^-2^

V

c f c f

^ cos— = 0, ^cf J

которое позволяет определить собственные частоты включения. Для выбранных значений параметров эти частоты сведены в таблицу 2. Здесь же даются значения частот, найденных с помощью численного моделирования. Отличие между значениями не превышает 2%.

Таблица 2. Сопоставление значений собственных частот, полученных двумя методами

Номер частоты	Значение частоты, КГц
	численная оценка	аналитическая оценка
1	1,79	1,81
2	3,58	3,64
3	5,37	5,45
4	7,16	7,27
5	8,95	9,09

В формулу (15) входят три геометрических –– R 1 , R 2 , l , и два независимых физических параметра — р и с / Однако данную формулу можно свести к виду, содержащему три независимых параметра 1 1 = R 1 /с/ , 1 2 = R 2 /с/ и 1 3 = l[c_f :

п 12 to 4Ф( 12 /11 )

cos to 1 3

+ sin to 1 3

п 12 to        П 12 to

4 Ф ( 1 2 / 1 1 ) [ ^{4 ф} ( ¹ 2 Д1 )

sin to 1 3

- cos to 1₃

J

= 0.

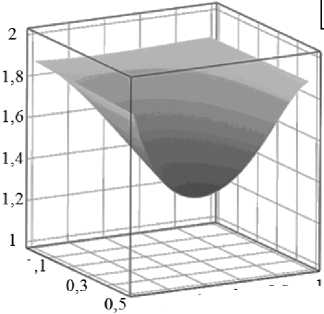
Такая форма записи частотного уравнения позволяет исследовать чувствительность собственных частот к геометрическим размерам включения. На рисунке 6 такая зависимость показана для первой собственной частоты.

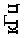
а

0, ^1= ^M

0 9 0,4 0,6 0,8

’ RM

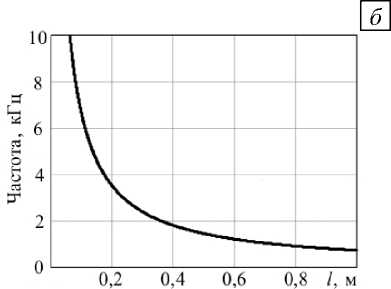
Рис. 6. Зависимость первой собственной частоты от геометрических размеров включения: при фиксированной длине l = 0,4 м ( а ) и при фиксированных радиусах R 1 = 0,05 м, R 2 = 0,025 м ( б )

• 4.    Заключение

Изучение распространения волн в трубе с включением начато с простейшей одномерной постановки задачи, что позволило оценить качественно влияние спектра включения на отраженную и прошедшую волны. Очевидно, что одномерная модель не позволяет описать всю сложность прохождения акустической волны в трубе с включением, поскольку на волновую картину влияет множество факторов: сама труба и ее окружение; параметры акустической среды, заполняющей трубу, и ее состояние (покой/течение); и наконец, параметры включения (как геометрические размеры, так и физические свойства). Их учет недоступен для полноценного аналитического исследования. В этих условиях возрастает роль тестовых задач, помогающих правильно интерпретировать качественную сторону получаемых результатов и понимать природу механизмов аналогичных явлений в более сложных моделях.

Численное моделирование открывает широкие возможности в решении прикладных задач, наиболее приближенных к реальности. Однако полномасштабная постановка задачи приводит к трудно анализируемым результатам. Поэтому в качестве следующего приближения рассмотрена частная математическая модель, в которой отсутствует влияние всех вышеперечисленных факторов за исключением геометрических размеров включения. Это позволило выявить особенности спектральных плотностей волн, отраженной от включения и прошедшей через него , а именно обнаружено наличие локальных экстремумов, что коррелирует с одномерной моделью. При этом положения экстремумов определяются спектром включения, а так как спектр зависит от геометрических размеров включения, то возможно решение обратной задачи, то есть определение геометрических размеров включения исходя из анализа прошедшей и отраженной волн.