Влияние движений, вызывающих усилия в бедренном суставе, на течение синовиальной жидкости

Описание динамических движений человека представляет собой сложную задачу, если учитывать непростое строение двигательной системы, и является одним из направлений биомеханики. Однако наиболее интересным является изучение вызванных чрезмерной нагрузкой дегенеративных изменений.

Бедренный сустав является одним из наиболее подверженных дегенеративным изменениям элементов опорно-двигательной системы человека при чрезмерном нагружении. Несмотря на значительные успехи в исследовании данной проблемы, механизм биосмазывания полностью еще не изучен. Эта задача стоит не только перед врачами и физиологами. Зная механические свойства сустава при чрезмерном нагружении, можно описать механизм его поведения при движениях, вызывающих усилия в суставе. Экспериментальные данные показывают, что давление на бедренный сустав в 50–200 раз больше веса человека (в зависимости от фазы движения) [1, 5]. Например, если вес человека равен 70 кг, то при движении величина силы достигает значений 3500–14000 Н.

Компьютерные технологии и численные методы всё чаще применяются при моделировании процессов, протекающих в человеческом организме, и приносят всё более значимые результаты, в частности, при исследовании бедренного сустава как биоподшипника и эндопротезировании [3, 4].

Цель работы заключалась в объяснении влияния движений человека на трибологические свойства биоподшипника. В процессе движения человека были

z

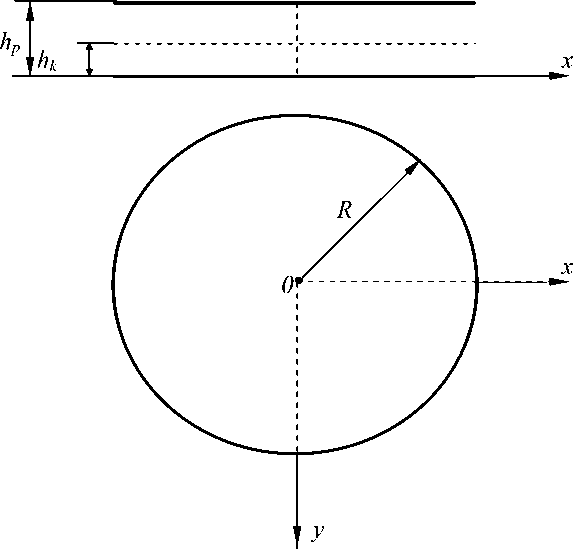
Рис. 1. Геометрия рассматриваемой задачи: R – радиус пластины; x , y , z – оси системы координат; O – центр системы координат; h p – начальное значение ширины суставной щели;

h k – конечное значение ширины суставной щели (после времени t )

вычислены трибологические значения биоподшипника путём решения динамической задачи, т.е. нестационарных уравнений для синовиальной жидкости в бедренном суставе посредством метода конечных элементов в программном пакете ADINA-F .

Задача была решена для упрощенной модели бедренного сустава, в которой не учитывались свойства суставного хряща – проницаемость и упругость.

• 1.    П ОСТАНОВКА ЗАДАЧИ

Геометрия суставной расщелины строилась по нормальным параметрам сустава. Движения (вставание и прыжок) были смоделированы как перемещение суставных поверхностей относительно друг друга.

Решение задачи движения жидкости было получено для сильно упрощенной геометрической модели сустава (рис. 1):

• •    суставная расщелина смоделирована как пространство между двумя параллельными круглыми пластинами;

• •    поверхности пластин являются жесткими и непроницаемыми (эластичностью и пористостью хряща пренебрегаем);

• •    начальное ( h p ) и конечное ( h k ) значения высот зазора были измерены, предполагая, что пластина смещается от начального положения в конечное за время t ;

• •    подвижная пластина перемещается только вдоль оси z ;

• •    поскольку данная задача состояла в том, чтобы получить качественные результаты, синовиальная жидкость рассматривалась как ньютоновская.

Геометрическая интерпретация исследуемой задачи представлена на рис. 1.

Течение жидкости описывается системой уравнений Навье–Стокса.

Система уравнений совместно с уравнением неразрывности течения выглядит следующим образом:

du    du   du p--+ u--+ v+

V 81    8x    8y

d ² u 8 ² u 8 ² u

d p

+ П э"+э"+ , 8 x    V 8 x ²    8 y ²    5 z ² 7

5 x'

5 y

dz'

d v     d v    d v     d v

p-- + u --+ v --+ w—

8 1     8 x    8 y     8 z

8 ² v 5 ² v 5 ² v

V

d p

_ +^П _ 2 + _n 2 + _n 2 , 5 y

V

5 x

5 y

8z'

8 w    d w   d w    d w

d p

^<8 ² w d ² w d ² w

d t     8 x     d y     d z

--+ П ----2" +--2" +--2"" ,

^~      8x2   8y2   8z2

d z

V

8 u 8 v 8 w

— + — + — = 0.(4)

5 x 5 y d z

Граничные условия:

u = 0, v = 0, w = 0 на поверхности неподвижной пластины,(5)

u = 0, v = 0 на поверхности подвижной поверхности,(6)

p = 0 на краях неподвижной и подвижной пластин.(7)

Здесь t – время перемещения поверхности от начального до конечного положения; u, v, w – компоненты вектора скорости V синовиальной жидкости относительно осей x, y, z (м/с); V = ( u , v , w ); p – давление жидкости (Пa).

Были использованы следующие значения параметров, которые характеризуют физиологические свойства сустава:

h p – начальное значение ширины суставной щели, h p = 200 мкм;

h k – конечное значение ширины суставной щели, h k = 40 мкм;

t – время смещения пластины от начального положения в конечное; при вычислении были использованы шесть точек, в которых были произведены вычисления: t 1 = 0,0005 с, t 2 = 0,001 с, t 3 = 0,003 с, t 4 = 0,005 с, t 5 = 0,0075 с, t 6 = 0,01 с;

R – радиус пластины, R = 0,01м;

П - динамическая вязкость синовиальной жидкости, n = 0,116 Па - с;

р - плотность синовиальной жидкости, р = 1000 кг/м³.

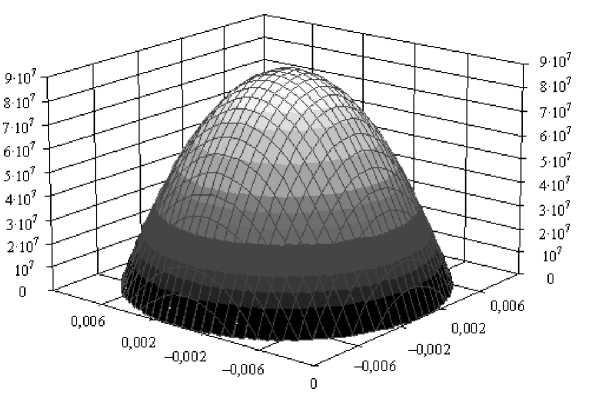
Рис. 2. Распределение давления в синовиальной пленке для варианта 2 (t = 0,001 с)

p макс , МПа

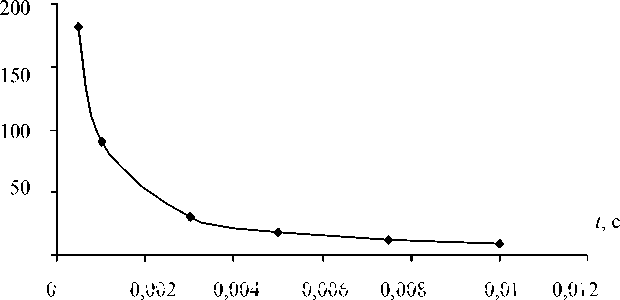
Рис. 3. Зависимость максимального давления p макс в синовиальной пленке от продолжительности воздействия на костные поверхности

Таблица

Результаты вычислений

Вариант	Время смещения пластин t , с	Нагруженность W , кН	p cр , МПа	p макс, МПа	u макс, м/с	v макс, м/с	w макс, м/с
1	0,0005	28,5	90,43	181,29	61,33	61,33	0,325
2	0,0010	14,1	44,92	89,93	30,72	30,72	0,166
3	0,0030	4,68	14,85	29,80	10,23	10,23	0,055
4	0,0050	2,81	8,90	17,95	6,14	6,14	0,033
5	0,0075	1,87	5,93	11,89	4,09	4,09	0,022
6	0,0100	1,41	4,45	8,92	3,07	3,07	0,016

Полученные значения суставной нагрузки, изображенные на рис. 5, лежат в диапазоне реальных значений [1, 5] и показывают качественную сходимость с вычислениями по микрополярной модели синовиальной жидкости [2].

Результаты, приведенные в таблице и на рис. 2–5 показывают, что динамика перемещений значительно влияет на поток синовиальной жидкости в бедренном

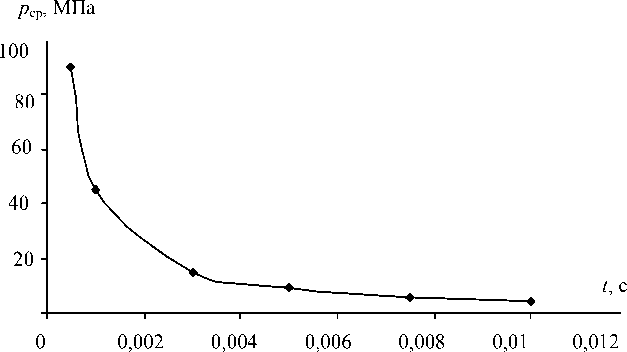
Рис. 4. Зависимость среднего давления ( p ср ) в синовиальной плёнке от продолжительности оздействия на костные поверхности

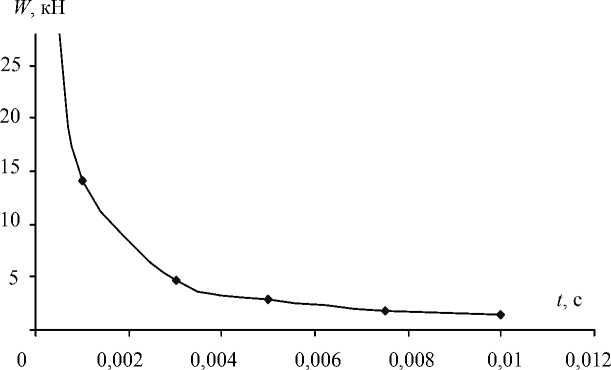
Рис. 5. Зависимость нагруженности сустава W от времени сближения суставных поверхностей суставе. Для очень небольшого промежутка времени (порядка 5⋅10-4 с), т.е. времени приземления после прыжка со значительной высоты, максимальное давление в суставе составило около 200 МПа (среднее давление достигает 100 МПа). Совокупная нагруженность составила 28,5 кН, и максимальная скорость потока синовиальной жидкости превышала 60 м/с. Этот эффект увеличения давления и потока синовиальной жидкости особенно явно прослеживается, если время воздействия меньше 10-3 с.

Для случая, когда минимальное время вычисления составило 10-2 с, максимальное давление синовиальной жидкости приблизительно равнялось 10 МПа (среднее давление достигало 5 МПа), совокупная нагрузка на сустав составила 1,4 кН, и максимальная скорость потока жидкости превышала 3 м/с.

Выводы

• •    Результаты численного моделирования нестационарного течения синовиальной жидкости в биоподшипнике показывают, что силовые движения человека вызывают значительное увеличение давления в суставной щели и других трибологических параметров.

• •    Следовательно, можно допустить, что превышение пороговых значений для нагрузки может стать причиной повреждений бедренного сустава в процессе выполнения интенсивных упражнений и занятий спортом.

• •    Поскольку упрощенная модель бедренного сустава была использована для вычислений без учета свойств хряща и неньютоновского характера синовиальной жидкости, полученные значения являются показателями качественных зависимостей.