Влияние физических параметров упругого ротора на несимметричных опорах на частоты его свободных колебаний

Бюллетень науки и практики / Bulletin of Science and Practice

Упругие валы, роторы, стержни являются динамическими моделями (рабочими основами, составляющими) многих технических конструкций [1–5, 13–16]. Исследования влияния физических параметров на частоты их свободных колебаний играет важную роль в вибродиагностике технических (механических) систем [6, 7, 14 ].

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №5. 2024

Определение частот колебаний упругого ротора на опорах в зависимости от его физических характеристик подразумевает рассмотрение динамической модели ротора как системы с конечным числом степеней свободы [8–12]. В данном исследовании подобная модель рассматривается для упругого вала (груза), расположенного на несимметричных опорах с учетом гироскопических свойств механизма [5, 7].

Расчетная динамическая модель упругого ротора массой m , c коэффициентами жесткостей c 1 , c 2 , несимметричных его опор (система с двумя степенями свободы) показана на Рисунке 1.

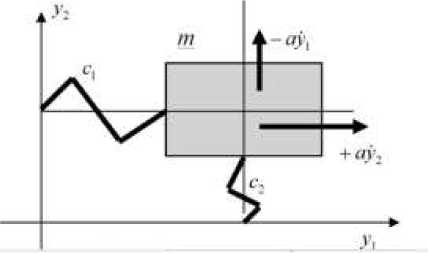
Рисунок 1. Ротор на несимметричных опорах

Если принять за обобщенные координаты прогибы ротора вдоль горизонтальной и вертикальной осей его симметрии, соответственно, функции

y = y 1⁽ x; t )   y 2 = y 2⁽ y ; t )

(где t

— время), то свободные колебания ротора можно описать дифференциальными уравнениями

[7]:

'- myi - сJ1 + ayi = 0;

- my 2 - с2 y 2 + ay2 = 0,

в которых коэффициент a гироскопической нагруженности ротора связывает угловую скорость его вращения с моментом инерции центра массы.

Без учета трения решения системы (1) принимаем в виде:

y i ( x , t ) = M 1 e i * ,   y ₂ ( y , t ) = M 2 e * * ,

где * — собственная частота, M 1 , M 2 , — амплитуды колебаний ротора.

Подстановка функций (2) вместе с их производными второго порядка в систему (1) приводит к системе линейных уравнений относительно ненулевых амплитуд колебаний:

- т * А - с А + ai * B = 0;

- т а? B - с₂В - ai * A = 0.

В итоге после раскрытия определителя матрицы системы (3) и приравнивания его к нулю получим частотное уравнение рассматриваемой спектральной задачи:

т² * ⁴ - ( т ( с + с ₂) + a ² ) * ² + сс = 0.

Рассмотрим теперь зависимости частот колебаний упругого ротора от коэффициентов жесткостей его несимметричных опор.

Численные расчеты по уравнению (4) значений частот колебаний ротора при различных значениях жесткостей опор представлены в Таблице 1 и графиках Рисунка 2 (к проводимым расчетам использовались команды и функционал математического пакета Maple [8]).

Таблица 1

ЗАВИСИМОСТЬ СОБСТВЕННЫХ ЧАСТОТ ш_к ( k = 1,2) КОЛЕБАНИЙ РОТОРА ОТ КОЭФФИЦИЕНТОВ ЖЕСТКОСТЕЙ НЕСИММЕТРИЧНЫХ ЕГО ОПОР ПРИ m = 1 кг

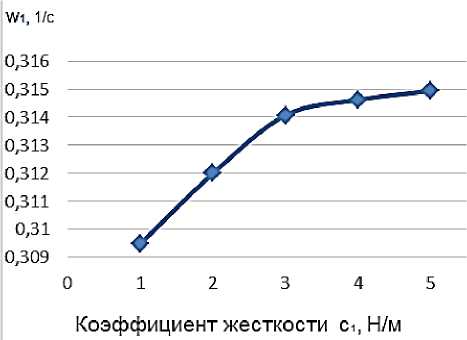
а)

Рисунок 2. Зависимость собственных частот ^ (а) и ® ₂ (б) колебаний ротора от коэффициента жесткости c 1 ( с ₂ = const ) его опоры

0,5

О

ек , H / м	c 2, H / м	- 1 ^ , с	- 1 (У 2 , с
1	0,1	0,3095	1,0218
2	0,1	0,3120	1,4290
3	0,1	0,3141	1,7439
4	0,1	0,3146	2,0102
5	0,1	0,3149	2,2452

W2, 1/С

0      1       2       3       4      5      6

Коэффициент жесткости Ci, Н/м

б)

По расчетам и построенным зависимостям можем отметить, что рост коэффициентов жесткостей несимметричных опор ротора ведет к росту значений частот его колебаний.

В Таблице 2 и графиках Рисунка 3 представлены зависимости значений частот колебаний ротора от его массы, в которых мы наблюдаем обратную связь: рост массы ротора ведет к уменьшению значений частот его колебаний.

Таблица 2

ЗАВИСИМОСТЬ СОБСТВЕННЫХ ЧАСТОТ ^ ^{k ( k} = ^1,2) КОЛЕБАНИЙ РОТОРА ОТ ЕГО МАССЫ (при жесткостях опор ^{c 1} = ¹ H / м , c ² = ^{0,1 H} / м )

m , кг	- 1 ^ 1 , с	- 1 ^ 2 , с
1	0,3145	1,0055
2	0,2230	0,7091
3	0,1822	0,5784
4	0,1789	0,5007
5	0,1413	0,4477

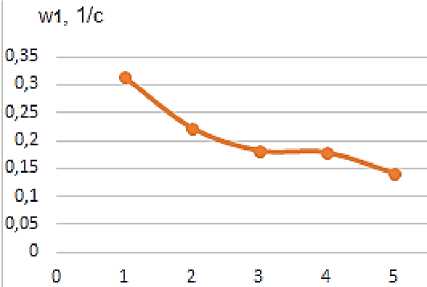
Масса ротора m, кг

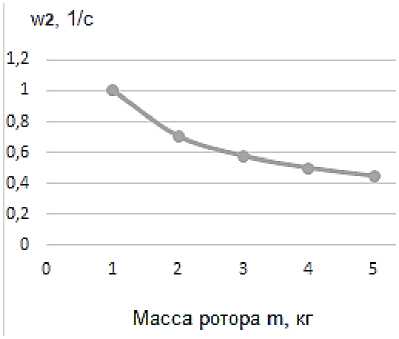
б)

Рисунок 2. Зависимость частот щ (а) и щ (б) колебаний ротора от его массы ротора (при жесткостях опор c j= 1 H / м , c ₂= 0,1 H / м )

а)

Аналогичные зависимости проведены и при других значениях параметров. Численные расчеты и при других физических параметрах рассматриваемого ротора на несимметричных опорах показывают, что увеличение жесткостей его опор (как одной, так и обоих) ведет к увеличению частот колебаний ротора, а увеличение массы ротора — к уменьшению частот. Заметим также, что установленные зависимости применяются при постановке и решении обратных задач, в частности, при задачах вибродиагностики ротора с учетом сохранения частот его свободных колебаний в прежних безопасных для функционирования и приработки механизма диапазонах.

Таким образом, в работе найдено частотное уравнение задачи свободных колебаний ротора на балочных несимметричных опорах, с помощью которого исследовано влияние на частоты колебаний физических параметров и условий закрепления механической роторной конструкции. Проведенные исследования важны при рассмотрении задачи виброзащиты подобной конструкции, связанной с изменениями его физических параметров. Проблему же сохранения безопасных частот колебаний ротора на несимметричных опорах можно будет решить постановкой обратной к рассмотренной здесь спектральной задачи.