Влияние флуктуаций диаметра сердцевины многомодовых оптических волокон на передачу сигналов в маломодовом режиме
Автор: Бурдин Антон Владимирович, Дельмухаметов Олег Равилевич, Макаров Виталий Сергеевич, Яблочкин Константин Александрович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 3 т.8, 2010 года.
Бесплатный доступ
Представлены результаты исследования влияния флуктуаций диаметра сердцевины многомодовых оптических волокон (ММ ОВ) на характер искажений формы сигнала, распространяющегося в маломодовом режиме. Рассматривались два образца типовых градиентных ММ ОВ 50/125 со слабым и, напротив, сильным проявлением дефектов профиля показателя преломления. Для разных значений среднеквадратического отклонения радиуса сердцевины выполнен расчет динамики маломодового сигнала на основе разработанной модели кусочно-регулярной многомодовой ВОЛП во временной области. Показано, что флуктуации диаметра сердцевины ММ ОВ оказывают наиболее существенное влияние на искажение формы импульса при его распространении в волокнах с сильным проявлением технологических дефектов профиля показателя преломления.
Многомодовое оптическое волокно с градиентным профилем показателя преломления, маломодовый режим, моды высших порядков, хроматическая дисперсия, дифференциальная модовая задержка
Короткий адрес: https://sciup.org/140191408
IDR: 140191408 | УДК: 621.315
Текст обзорной статьи Влияние флуктуаций диаметра сердцевины многомодовых оптических волокон на передачу сигналов в маломодовом режиме
Задачи моделирования процессов,возникающих при распространении оптических сигналов по многомодовым оптическим волокнам (ОВ)в маломодовом режиме,в полном объеме возникли и были сформулированы в середине 90-х годов на стадии разработки стандартаIEEE 802.3z (Gigabit Ethernet)[1-2].Наиболее полно данное направление представлено в монографии [3]и публикациях авторов [4-10],непосредственно принимавших участие в разработке стандартов IEEE 802.3z и 802.3ae.Данные работы,в первую очередь, были ориентированы на теоретическое исследование эффекта дифференциальной модовой задержки (DMD – Differential Mode Delay)как основного фактора искажений сигналов,ограничивающих совместное применение лазеров и многомодовых ОВ.В частности, проявлений DMD в зависимости от условий ввода излучения выхода лазера в сердцевину ОВ и характерных дефектов градиентного профиля реальных воло-кон.Отдельное внимание уделяется имитационному моделированию процессов формирования,преобра-зования и обработки сигналов в передающих и приемных оптических модулях активного оборудования систем передач.Поскольку по стандарту IEEE 802.3z длина линии не должна превышать 500 м,а скорость передачи - 10 Гбит/С,в указанных работах,как пра-вило,пренебрегают взаимодействиями и смешением мод,обусловленными нерегулярной структурой ОВ, микро- и макроизгибами волокон.В отдельных случаях вводят поправочные коэффициенты и «штрафы»
по так называемому модовому шуму.Однако и здесь акцент делается в основном на перераспределении мощности между модовыми группами при прохождении оптического сигнала через соединения волокон/ патчкордов в распределительных боксах или оконечных устройствах коммутации.
Вместе с тем,в [5; 11-14]при сопоставлении данных экспериментальных измерений DMD на образцах ОВ и резервных волокнах линий передачи было выявлено,что в отдельных случаях взаимодействие и смешения мод в линии оказывают существенное влияние на характер искажений импульса,обусловленных DMD.Очевидно,что с увеличением скоростипередачи и протяженности линии данный эффект будет проявляться сильнее.
Еще одно направление,в связи с которым возникает необходимость учета взаимодействия и смешения мод в многомодовой оптической линии передачи при моделировании процессов распространения в маломодовом режиме – оценивание значений модовой задержки по результатам сравнения формы модельного и измеренного оптических импульсов.Так,еще в работе [15]была продемонстрирована возможность использования для этих целей метода WKB с последующим простым наложением составляющих сигнала.
Одна из наиболее существенных причин проявления связей модвОВ – изменениядиаметра сердцевины [1 6].Предлагаемая работа посвящена теоретическим исследованиям влияния данного фактора на характер искажений формы сигнала,распространяющегося по традиционным телекоммуникационным кварцевым слабонаправляющим многомодовым ОВ с градиентным профилем показателя преломления в маломодовом режиме передачи.
Решение задачи о длинном нерегулярном волново-де,параметры которого меняются вдоль его оси случайным образом,классическими методами в строгой постановке [17-23]требует значительных вычислительных ресурсов и труднореализуемо.Поэтому для приближенного описания такой волноведущей структуры использовали модель кусочно-регулярной линии передачи [21-23]с кварцевыми слабонаправляющими многомодовымиОВ сосесимметричнымградиентным профилем показателя преломления и одной внешней сплошной оболочкой на регулярных участках.Полага-ли,что волокна на границах регулярных участков соединены строго соосно.
Моделирование процессов распространения оптического излучения в такой линии требует выполнения расчетов параметров мод,включаягрупповуюскорость и коэффициент хроматической дисперсии,для каждого регулярного отрезка ОВ с градиентным профилем сложной формы,а также коэффициентов связи мод на каждом стыке таких регулярных ОВ.Учет сложной формы профиля (наличие дефектов по оси ОВ и т.п.) является обязательным условием при моделировании маломодового режима передачи многомодовой ВОЛП. При этом моделирование случайного характера флуктуаций диаметра сердцевины ОВ приводит к необходимости многократных вычислений указанных выше параметров.Как следствие,используемые методы расчета параметров мод в ОВ и их соединениях должны предъявлятьсравнительнонизкие требованияквычис-лительным ресурсам.
В данной работе был использован модифицированный метод приближения Гаусса,обобщенный на случай расчета параметров передачи направляемых мод произвольных порядков,распространяющихся в многомодовых ОВ с осесимметричным профилем показателя преломления произвольной формы и одной внешней сплошной оболочкой [24].Метод отличается относительно малыми погрешностями для ОВ с профилями достаточно сложной конструкции – в частно-сти,профилям реальных градиентных многомодовых ОВ,которые отличаются локальными дефектами и флуктуациями.При этом обеспечивается переход к аналитической форме записи выражений для базовых параметров передачи модовых компонентов сигнала,а также коэффициентов связи мод на границах регулярных участков,что существенно снижает время вычис-лениядажев случаеоценкихарактеристикмод высших порядков.
Приложение модифицированного приближения Гаусса в задачах моделирования линейного тракта кусочно-регулярной многомодовой ВОЛП
Приближение Гаусса базируется на аппроксимации полей мод волоконного световода с некоторым заданным профилем показателя преломления полями мод волоконного световода с идеальным неограниченным параболическим профилем показателя преломления [19]:
где R = r / a- – нормированный радиус; r – радиальная координата; Ro p0 /a – нормированный радиус пятна моды; po – радиус пятна моды; – полином Лагерра; l и m – азимутальный и радиальные порядки моды LP lm соответственно.
Указанная аппроксимация сводится к определению эквивалентного радиуса пятна моды R0 путем решения характеристического уравнения,которое выводится из вариационного выражения для посто- янной распространения,записанного для исследуемого слабонаправляющего волоконного световода с заданным профилем.Найденный параметр является в рамках данного приближения базовым и полностью определяет искомые характеристики моды.
В отличие от известных решений на основе приближения Гаусса [19; 25-29], ОВ с произвольным осесимметричным профилем показателя преломления рассматривается как волоконный световод с многослойным профилем показателя преломления. При этом профиль в интервале от центра сердцевины до внешней оболочки исследуемого волокна представляется в виде конечного числа N слоев,в пределах которых значение показателя преломления остается постоянным [23-24]:
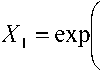
-^?Уд Y ^ + qV k'P • УУ,]^ ^.pXR^N^"
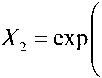
^0 J <7=0
^p'-R?
(£ + l)2)2^;2 ^иду^к^Р
VV Л0 J <7=0 p=0 P '^0 1N
nW=v’
0<^<^-l;
(/ + 777 - 1)!(3/ + 2/И-1)
(/>7-1)!
2/77—2 2/77—2
+2/2^Dj7/ + /-l)!-4/^q(67 + /)! ;
q=0 q=0
nN, 1 < R< +co ,
а функция произвольного профиля может быть записана в следующем виде:
/7,
к k-v\
N N
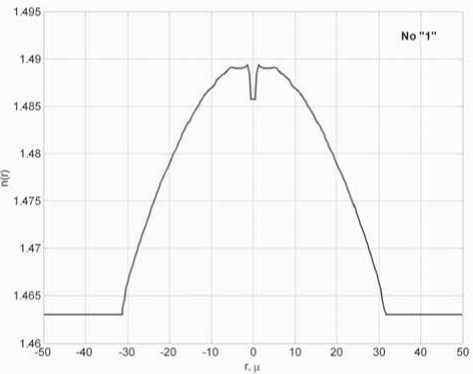
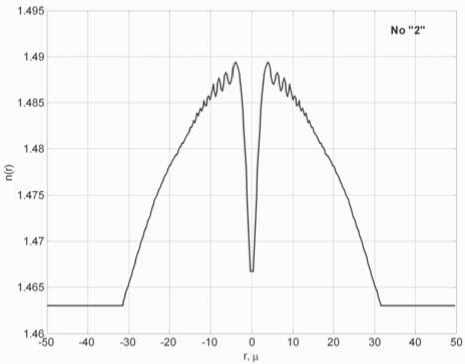
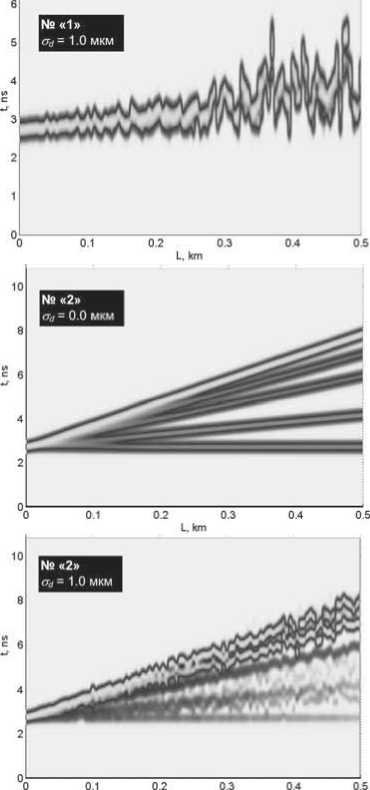
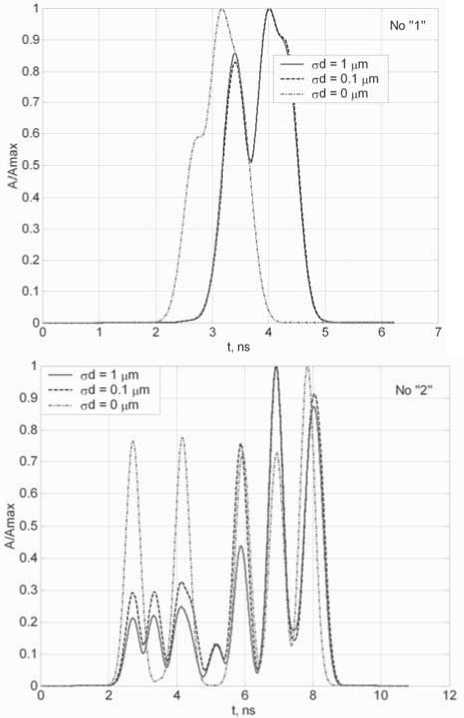
0 1, 1 < R< +00, , П0 ~Пк „ _ „ x — где ^k - 2 2 – параметр профиля; n0 – мак- 77O- - 77- симальное значение показателя преломления; nk – показатель преломления k-го слоя (k = 0; 1; 2 … N), при этом показатель преломления и функция профиля связаны следующим соотношением [19-23]: 772(^)=«о[1-2ЛЖ, где A = (и02 - Hn^tio – параметр высоты профиля; nN – показатель преломления внешней сплошной оболочки. Подобное представление профиля исследуемого ОВ позволяет в результате выполнения необходимых преобразований, подробно изложенных в [24], перейти от известной [19] интегральной формы записи вариационного выражения для квадрата параметра моды в сердцевине U2к аналитической, представляющей собой конечные вложенные суммы вида: min(,m-l) q / j q \ m-A rq-p \ m-\ / p=max(0,^-m+l) min(^,m-l) c,= ^Lu^iq,,,,^1^ /7=тах(0,у-т+1) ^q V^m-A /’ ^q Wm-l / – коэффициенты полиномов Лагерра и ^т-\ , соответственно, определяемые из формулы явного выражения полинома Лагерра [30]: У = kan0 -JlA. – нормированная частота; к = 2л/2 – волновое число; X – длина волны. В рамках общего алгоритма приближения Гаусса [19]базовый параметр аппроксимации – эквивалентный нормированный радиус пятна моды – определя- ется путем решения характеристического уравнения вида 8R0 В результате дифференцирования (5)с учетом (7)и выполнения необходимых преобразований характеристическое уравнение приводится к следующему виду: 1 \lm-2 l+q где So = ехр ^Dq^ \ ”() 7 9=0 Р=о !/ + )' р^У связан c постоянной распространения p следующим известным соотношением [19-22]: Sv = exp к2 N2R2 TT2 p2 =k2n2 - — . (11) a 2 m-2 l+q PLDX q=0 pA) V + + k1” (e 2 p\R2p N2pVN2 ° Для оценки значения групповой скорости направляемой моды заданного порядка предлагается воспользоваться известным соотношением [19-22], предварительно переписанным относительно первой производной квадрата постоянной распространения: S2 = exp ^o » 4^p\R2p N2p № Po Таким образом, анализ многомодового слабонаправляющего волоконного световода с произвольным осесимметричным профилем показателя преломления, ограниченным одной внешней сплошной оболочкой, включает в себя выполнение следующих этапов. Предварительно профиль исследуемого ОВ задается в виде N слоев с помощью (2)-(4). Затем для моды заданного порядка LPlmв результате численного решения уравнения (8) определяется нормированный эквивалентный радиус пятна моды R0, который должен удовлетворять условию существования направляемых мод [19-22]: _ Qcd _ lite QX _ ЛяРс дЛ _ Vg ”^p”-^T^p” x- ep1 ~ . (12) k-pc ax я ap2 ’ где co – угловая частота; c – скорость света в вакууме. Далее в результате дифференцирования (1 1) выражение для первой производной постоянной распространения приводится к виду: dp2 lk2n2| e dn2 1 du2 ax x ax a2 ax ‘ При этом в рамках предложенной модификации приближения Гаусса первая производная квадрата параметра моды в сердцевине,полученная в результате дифференцирования (5),имеет следующий вид: knN < P< kn0, (9а) au2 ax где P – постоянная распространения, и неравенству 2M 8R^ pV2_ Rl ax ax (9б) где ^O – нормированная мощность моды, переносимая в сердцевине ОВ [19]. Данный параметр в рамках приближения слабонаправляющего оптического волновода [19] с учетом (1)-(4) описывается выражением вида [31]: ^v’-xy^+v’-ypyvx-x.v О A ^=q О A ( 1 \lm-l l+q где xW=exp -— ^D^ 1) 7 9=0 —^ n I P2P+3 ,=o p! л() 2 m-2 l+q к2 n2r2 Подстановка R0, удовлетворяющего (9а) и (9б), в выражение (3) позволяет оценить параметр моды в сердцевине U, который непосредственно q=0 p=0 V+qy. k'- r k1 , p\R2p+3 N21\N2 P° ^_(/±ЛГЛ±1Г f (t + 1)2 ^ ^!С+3N"P ( N2 -pR« В свою очередь, полученное в результате дифференцирования уравнения (8) и выполнения соответствующих преобразований аналитическое выражение, описывающее первую производную нормированного эквивалентного радиуса пятна моды, имеет следующий вид: SR^ 8Л S,, +У 52 ^ 0 UP 52 52 -2V2 • где k=0 62^2 _ 2 (Э2п2 6n2 4 8n2 ) 1 d2U2 (17) __ 1^ ______и । _ " ( 622 22 2 52 J a2 522 а также повторного дифференцирования (14)и (15), можно получить выражения,связывающие параметр D с первой и второй производными квадрата параметра моды в сердцевине SU2/82, 5 2U 2/5Х и нормированного эквивалентного радиуса пятна моды 8Rn /8Х, 8 2Ro /8Л2. Эти формулы достаточно гро-моздкие,имеют вид конечных вложенных сумм и представлены в полном объеме в работе [24]. Спектральную зависимость материалов сердцевины и оболочки кварцевых многомодовых ОВ предлагается аппроксимировать хорошо известной формулой Селлмейера [19-22].Однако и в этом случае выполняется переход к производным квадрата показателя преломления 8n2/8X ; 8 2п2/8Л2. Это существенно упрощает вывод выражений для производных параметров профиля – например, Aи ilk, а также нормированной частоты V. Наконец, использование приближения Гаусса обеспечивает переход к аналитической форме записи коэффициентов связи мод [31]на границах регулярных участков через интеграл перекрытия полей падающей и возбуждаемой мод [32]: N2R^ ) ^ ^ ^uqyk2p Z-i^qZ-i । nip+i <7=o p^P-1'Ao Прч Г (7+ рУУ + qy PPPtU SV1=exp (^Л x^ ^Uq^byV^ ^ “^ p\N2pRy+3 Аналогичным образом, переписав известное [19-22] выражение для коэффициента хроматической дисперсии относительно производных квадрата постоянной распространения: 2лс 2 -^ + 2^ 52 52 2 a/?2 '- 1 8p2 \2 ^лрс 2 52 6222p2 ( 62 в результате повторного дифференцирования (13): r^p + q + I-k-l) | P2+P2 | I t'(p-k)r(q-k)k'.\vp2-p2 J ’ где p и q –радиальные порядкипадающей ивозбужда-емой моды соответственно; Pp И Pq – радиусы пятна моды p и q соответственно; Г – гамма-функция. Таким образом,предложенная модификация приближения Гаусса позволяет реализовать модель линейного тракта кусочно-регулярной многомодовой ВОЛП во временной области.Волокно разбивается на регулярные участки,в пределах которых параметры световода остаются постоянными.Предполагается, что каждая направляемая мода,возбужденная источником излучения (или падающей на границу регулярного участка модовой компонентой сигнала),пере-носит оптический импульс гауссовой формы.Также предполагается,что в пределах регулярного участка отсутствуют процессы взаимодействия и смешения мод.Сигнал претерпевает искажение за счет разброса значений групповых скоростей модовых компо-нентов,или,иными словами,благодаря проявлению DMD.Кроме того,за счет хроматической дисперсии происходит увеличение длительности импульса,пе-реносимого каждой возбужденной направляемой мо-дой,распространение которой поддерживается на заданном регулярном участке ОВ.Перераспределение мощности внутри модового состава сигнала за счет нерегулярной структуры реального ОВ учитывается путем оценки значений коэффициентов связи мод на стыках регулярных участков.Следует отметить, что в рамках данной работы рассматриваются только направляемые моды,представляющие наибольший интерес с точки зрения исследования динамики импульса в нерегулярном многомодовом ОВ.Тем не ме-нее,потери мощности сигнала за счет преобразования направляемых мод высших порядков в вытекающие, а также на отражение фактически учитываются при расчете коэффициентов связи на стыках регулярных участков. Результаты расчета Теоретические исследования влияния флуктуаций диаметра сердцевины на характер искажения формы передаваемого в маломодовом режиме сигнала были выполнены для двух образцов кварцевых многомодовых ОВ 62,5/125.Распределение значений показателя преломления задавалось в соответствии с протоколами измерения профилей реальных ОВ,воспроизве-денных на рис.1.Образцу «1» соответствует слабый центральный дефект,в то время как для образца «2», напротив,характерны высокие значения радиуса и глубины провала,а также флуктуации профиля в центральной области сердцевины. Рассматривалось распространение оптического импульса гауссовой формы исходной длительности 200пС,возбуждаемогоисточникомVCSEL надлине волны X = 850нмиширинойспектраизлучения лл=1нм, по указанным образцам многомодовых ОВ протяженностью 500 м каждый.Ввод сигнала в сердцевину ОВ с выхода VCSEL осуществлялся в условиях осевого смещения d = 2мкм,при этом,согласно [33-34],ис-ходный импульс содержал следующие пять модовых компонентов: LPо!, LP02, LPп, LP12, LP21, LPа. Длина регулярного участка для обоих образцов волокон выбиралась равной 5 м.В работе [16]было по-казано,что флуктуации диаметра сердцевины вдоль продольной оси многомодовых ОВ подчиняются нормальному закону распределения.Предполагалось,что форма профиля при изменении диаметра сердцевины остается неизменной.Параметры профилей,задава-лись в интервале r = 0 … a с помощью 120 точек.В качестве среднего значения использовались исходные данные,представленные на рис.1,а дисперсия выбиралась равной 3,75·10-4.Аналогичным образом задавались флуктуациидиаметра сердцевины ОВ:среднее значение соответствовало номинальному диаметру 62,5 мкм,дисперсия принималась равной с<1 = 1 мкм и 0,1 мкм.При этом полученные значения не выходили за границы удвоенного максимально допустимого отклонения диаметра от номинального,которое для подавляющего большинства многомодовых ОВ,со-гласно спецификациям [35],не превышает ±3 мкм. Анализ регулярных многомодовых волоконных световодов,составляющих модельные образцы ОВ, с помощью модификации приближения Гаусса по-казал,что максимальное значение радиального порядка направляемой моды, удовлетворяющей условиям (9а)и (9б),не превышает m = 6 как в случае cd = 1 мкм, так и Рис. 1. Профили показателя преломления исследуемых образцов градиентных многомодовых ОВ 62,5/125 На рис.2представлены результаты расчета диаграмм динамики возбуждаемого при указанных условиях оптического импульса при его распространении по образцам ОВ «1» и «2» длиной 500 м для разной степени флуктуации диаметра сердцевины.На рис.3 приведены модельные формы сигналов на выходе ВОЛП с многомодовыми ОВ «1» и «2». Сравнительный анализ полученных результатов по-казывает,чтов обоих случаях формы сигналов,постро-енные без учета нерегулярности ОВ и,соответственно, с учетом процессов взаимодействия и смешения модовых компонентов,различаются достаточно сильно. L, km L km Рис. 2. Диаграммы распространения сигналов При этом для образца «2» с более ярко выраженными дефектами профиля показателя преломления отмеченное расхождение проявляется сильнее. С точки зрения сравнения формы импульсов, полученных для разных значений параметра СГд, для ОВ «1» наблюдается практически полное совпадение, в то время как для волокна «2» можно зафиксировать не только отличие амплитуд модовых составляющих, но и появление дополнительной компоненты сигнала. Рис. 3. Формы импульсов на выходе образцов ОВ «1» и «2» длиной 0,5 км для разных значений СКО Заключение В работе представлены результаты исследований влияния степени флуктуаций диаметра сердцевины ОВ на характер искажений сигнала в многомодовой ВОЛП, работающей в маломодовом режиме, с учетом DMD, хроматической дисперсии мод высшего порядка и связей модовых компонентов. Предложена модель кусочно-регулярной многомодовой ВОЛП, в основе которой расчет параметров передачи направляемых мод на каждом регулярном участке осуществляется с помощью предложенной модификации приближения Гаусса, обобщенной на случай анализа слабонаправляющих многомодовых ОВ с произвольным осесимметричным градиентным профилем показателя преломления, ограниченным одной сплошной внешней оболочкой. Метод обеспечивает низкую погрешность вычислений характеристик направляемых мод произвольного порядка при сравнительно низких требованиях, предъявляемых к вычислительным ресурсам. Так, время вычисления параметров 24 мод LPlm (l = 0 … 3; m = 1 … 6) на каждом из 100 регулярных участков, составляющих ОВ длиной 500 м при задании профиля с помощью 120 точек и последующем построении диаграммы распространения сигнала не превысило 15 мин. (Intel® Pentium® M740; 1,73 ГГц; RAM 512 Мб). Исследования были выполнены для двух образцов многомодовых ОВ, отличающихся параметрами дефектов профиля показателя преломления. Показано, что изменение диаметра сердцевины ОВ оказывает наиболее существенное влияние на искажение формы импульса при его распространении в ОВ с сильным проявлением DMD, которое обусловлено наличием значительных технологических дефектов профиля показателя преломления. Напротив, для более «качественного» образца ОВ со слабо выраженным центральным провалом профиля существенных расхождений между формой импульса на выходе ВОЛП для разных значений параметра не наблюдалось. В то же время для обоих образцов волокон были выявлены значительные расхождения между формой сигналов, построенных без учета нерегулярности ОВ и, соответственно, с учетом процессов взаимодействия и смешения модовых компонентов. Как и в предыдущем случае, у образца с более сильно выраженным дефектом профиля расхождение больше.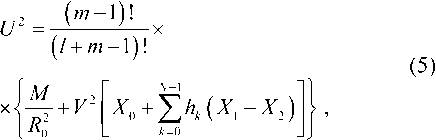
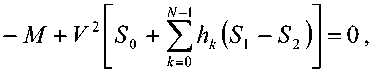
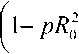
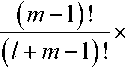
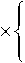
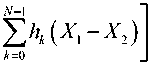
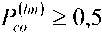
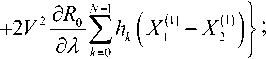
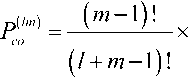
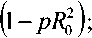
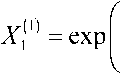
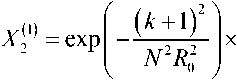
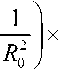
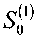
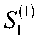
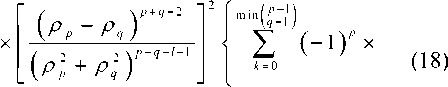
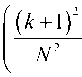

Список литературы Влияние флуктуаций диаметра сердцевины многомодовых оптических волокон на передачу сигналов в маломодовом режиме
- Cunningham D., Noweli M., Hanson D. Proposed worst case link model for optical physical media dependent specification development//IEEE 802.3z Task Force. Presentation materials, January 1997 meeting. -1997.
- Abbot J.S., Hackert M.J., Harshbarger D.E., Cunningham D.G., Di Minico Ch.T., White I.H. Analysis of multimode fiber behavior with laser sources in the development of the Gigabit Ethernet fiber optic specifications//IEEE 802.3z Task Force. Presentation materials, November 1998 meeting. -1998.
- Bottachi S. Multi-Gigabit transmission over multimode optical fibre. Theory and design methods for 10GbE systems. West Sussex: Wiley, 2006. -654 p.
- Cunningham D.G., Nowell M., Hanson D.C., Kazovsky L. The IEEE 802.3z worst case link model for optical physical media dependent specification//IEEE 802.3z Task Force. Presentation materials, February 1998 meeting. -1998.
- Raddatz L., White I.H., Cunningham D.G., Nowell M.C. An experimental and theoretical study of the offset launch technique for the enhancement of the bandwidth of multimode fiber links//IEEE Journal of Lightwave Technology. 1998. Vol. 16(3). -P. 324-331.
- Webster M., Raddatz L., White I., Cunningham D. A statistical analysis of conditioned launch for Gigabit Ethernet links using multimode fiber//IEEE Journal of Lightwave Technology. Vol. 17(9)? 1999. -P. 1532-1541.
- Pepeljugoski P., Golowich S., Ritger A., Kolesar P., Risteski A. Modeling and simulation of next-generation multimode fiber links//IEEE Journal of Lightwave Technology. Vol. 21(5), 2003. -P. 1242-1255.
- Pepeljugoski P., Kuchta D. Design of optical communications data links//IBM Journal of Research and Development. Vol. 47(2/3), 2003. -P. 223-237.
- Shaulov G., Whitlock B. Multimode fiber communication system simulation//IEEE 802.3aq Task Force. Presentation materials, July 2004 meeting. -2004.
- Morikuni J., Mena. P., Whitlock B. K., Scarmozzino R. Link-Level Design, Analysis, and Simulation of Multimode Data Communication Systems//19th Annual National Fiber Optic Engineers Conference (NFOEC). Technical Proceedings, 2003. -P. 858-867.
- Cunningham D., Nowell M. EMB, WCMB and ROFL Testing//IEEE 802.3z Task Force. Presentation materials, July 1997 meeting. -1997.
- Aronson L., Buckman L. Guide to HP Labs ROFL/OFL fiber measurements from 12/15/97 -12/19/97//IEEE 802.3z Task Force. Presentation materials, February 1998 meeting. -1998.
- Ristetski A., Borich E., Ewen J., Tierno J., Pepeljugoski P. DMD measurements and equalization simulations for 62,5-and 50-mm legacy multimode fibers at 1300 nm//IEEE Photonics Technology Letters. Vol. 16(8), 2004. -P. 1960-1962.
- Бурдин А.В. Дифференциальная модовая задержка кварцевых многомодовых оптических волокон разных поколений//Фотон-Экспресс. T. 69/70, № 5/6, 2008. -C. 20-22.
- Ramskov-Hansen J.J., Nicolaisen E. Propagation in graded-index fibers: comparison between experiment and three theories//Applied optics. Vol. 17(17), 1978. -P. 2831-2835.
- Krawarik P., Watkins L. Fiber geometry specifications and its relations to measured fiber statistics//Applied optics. Vol. 17(24), 1978. -P. 3984-3989.
- Кацелененбаум Б.З. Теория нерегулярных волноводов с медленно меняющимися параметрами. М.: Мир, 1961. -216 с.
- Барыбин А.А. Электродинамика волноведу-щих структур. Теория возбуждения и связи мод. М.: Физматлит, 2007. -512 с.
- Снайдер А., Лав Дж. Теория оптических волноводов. Пер. с англ. М.: Радио и связь, 1987. 656 с.
- Маркузе Д. Оптические волноводы. Пер. с англ. М.: Мир, 1974. -576 с.
- Унгер Х.-Г. Планарные и волоконные оптические волноводы. Пер. с англ. М.: Мир, 1980. -656 с.
- Okamoto K. Fundamentals of optical waveguides. San Diego: Academic Press, 2000. -430 p.
- Бурдин В.А. Основы моделирования кусочно-регулярных волоконно-оптических линий передачи сетей связи. М.: Радио и связь, 2002. 312 с.
- Bourdine A.V. Method for chromatic dispersion estimation of high-order guided modes in graded index single-cladding fibers//Proceedings of SPIE. Vol. 6605, 2006. -P. 660509-1-66050913.
- Mishra P., Hosain S., Goyal C., Sharma A. Scalar variational analysis of single-mode, graded core, W-fibers//Opt. Quantum. Electron. MTT-30, 1982. -P. 1-5.
- Peng G., Ankiewich A. New evanescent field approximation for weakly guiding fibers//IEEE Proc. J. Vol. 138, 1991. -P. 33-38.
- Hosain S., De Fornel F., Goudonnet J. Characterization of single-mode graded-index fibers: a new method based on transverse offset splice loss//Microwave Optic. Technol. Lett. No. 7, 1994. -P. 301-304.
- Chao S.-C., Tsai W.-H., Wu M.-S. Extended Gaussian approximation for single-mode graded-index fibers//IEEE Journal of Lightwave Technology. Vol. 12, 1994. -P. 392-395.
- Wu M.-S., Lee M.-H., Tsai W.-H. Variational analysis of single-mode graded-core W-fibers//IEEE Journal of Lightwave Technology. Vol. 14(1), 1996. -P. 121-125.
- Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979. -830 с.
- Андреев В.А., Бурдин А.В. Многомодовые оптические волокна. Теория и приложения на высокоскоростных сетях связи. М.: Радио и связь, 2004. -248 с.
- Срапионов В.А. Связь мод в стыках оптических волокон с разбросом параметров//Электросвязь. №10, 1985. -C. 10-12.
- Valle A., Sarma J., Shore K. Spatial hole burning and self-focusing in vertical cavity surface emitting diodes//IEEE Journal of Quantum Electronics. Vol. 31(8), 1995. -P. 1423-1431.
- HFE4092-341 850 nm VCSEL Datasheet. Honeywell Inc. -2003.
- Листвин А.В., Листвин В.Н., Швырков Д.В. Оптические волокна для линий связи. М.: ЛЕСАРарт, 2003. -288 с.


