Влияние функции Дирака к затягиванию потери и устойчивости решений сингулярно возмущенной задачи

Бюллетень науки и практики / Bulletin of Science and Practice

В работе неоднородная часть будет обобщенная сингулярная функция Дирака. Эта функция сильно влияет к явлению затягиванию потери устойчивости решений сингулярно возмущенной задачи. Цель исследования: доказать асимптотическую близость решения сингулярно возмущенного дифференциального уравнения и соответствующего невозмущенного уравнения в случае смены устойчивости

Материалы и методы исследования

Рассмотрим задачу

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №4. 2024

8 x ' ( t , s' ) = Л (t ) x ( t, E ) + e [ S( t — a ) + f ( t , x(t , £ ) ]

X ( 1 0 , 8 ) = X °( 8 )   x ^{0( £} )| = O^(£ )

где ⁰ <  ⁸ — малый параметр, ⁶ 0^ ^ , ^{x (} t ^{, 8} ) — искомая неизвестная функция, S ⁽t - a ) — функция Дирака которая имеет значение только в точке a .

Для решения правой части поставленной задачи (1) требуется выполнение следующих условий:

~

U1. g(t) , f (t, x) 6 Q( ) — пространство аналитических функций в области Н , f (t,0) - 0

,

(f ( t ,~) — f ( t ,~) <  M x

~~

I |, ⁰<  M — некоторая постоянная.

U2 Л ( t ) = а ( t ) + в ( t) Re Л (t) = а ( t ) <  0 — ж< t <  0 • ^{Re Л ( Т} 0 )   ^{a ( T ) 0 в ( Т} 0 ) ^ ⁰

Re Л ( t ) = a (t ) >  0 0 <  t <+x.

,.

Имеет место следующая теорема:

Теорема. Пусть выполнены условия U1-U2. Тогда ⁶ [/^0,^1 решение задачи (1)-(2) существует, единственно и для него справедлива оценка

|X(t, 8)| < CxJ где C — const.

Доказательство. Задачу (1)-(2) заменим интегральным уравнением

t

Л

t

t

x ( t , s ) = x ⁰( s )exp — j Л ( s ) ds + j exp —J Л ( s ) ds • [ £ ( I ⁸ t 0          ) 1 0      \ ⁸ T          )

\

t 0

)

t 0

\

т — a ) + f ( t , x ( t , 8 ) ] d r

Для доказательства существования решения уравнения (4) применим метод последовательных приближений.

Последовательные приближения определим следующим образом:

x 0 ( t , 8 ) = 0

t

t

t

x_n ( t , 8 ) = x ⁰( 8 )exp —J Л ( s ) ds + J exp —J Л ( s ) ds -\_3 ( т — a ) + f ( t \ ⁸ t 0          ) t 0      \ ⁸ t         )

\

t 0

)

t 0

, x_n — j ( t , 8 ) ] d r

,

где n ⁶ N .

t u (t, t0) = Re j Л( s) ds

Далее              t ⁰

H_o = { t : u ( t , t ₀) <  0 }

Определим область ^{0         0}     ’ .

H

Из (5) оценим последовательные приближения на замкнутой области 0 . Тогда

/

t

к

t

t

A

x_l ( t , z ) = x ⁰( z )exp — | Л ( s ) ds + ^д(т - a )exp — | Л ( s ) ds d r I z t J                I z T       J

к

t 0

.

Отсюда имеем:

t

t

X j ( t , £ ) = x ⁰( z )exp —J Л ( s ) ds 1 + exp | — J Л ( s ) ds

к

к

Здесь учтено что,

t 0

к

a

.

t

t

\

t

tt   t

J d ( r - ^a )exp —J Л ( s ) ds d T = exp I — j Л ( s ) ds t 0              к £ T         j         к £ a

t

Определим модуль решений

t

t

.

к

I x ,( t , z )| <  x⁰

к t 0

Будет пятеро случаи:

.

1). Если ^⁰ a то длину задержки решений определяет величина

t

x ⁰ ( z ) exp —J Л ( s ) ds

к

t 0

к

;

• 2) . Если 0° >  a то длину задержки решений определяет величина

  
  

  t

  
  

  к

  
  

  exp ¹ | Л ( s ) ds к £ a        j

  
  

  ^;

  • 3) . Если 0^й  a то длину задержки тоже определяет величина

  
  

  T

  
  

  t

  
  

  к

  
  

  exp ¹ | Л ( s ) ds к £ a        j

  
  

  ;

  • 4) . Если ^a ^ ^х , то функция Дирака будет $ ⁽t ^{- a} ) = ⁰ и длину задержки решений определяет величина

  
  
  
  

  t

  
  

  x ⁰ ( z ) exp —J Л ( s ) ds к ^z t 0

  
  

  к

  
  

  к

  
  
  
  

• 5) . Если ^a = ⁰, то длину задержки определяют величина

  t

  
  
  

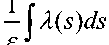
  к

  
  

Это означает что, в этом случае явления задержки потери устойчивости не выполняется.

Отсюда появится ограничение на постоянную a . Этот случай не будем рассматривать.

t ^е H 0.

В остальном случае имеет места оценка

|x 1 ( t , £ )| <  C exp

u ( t , 1 0 )

£

t

u(t, t0) = Re J Л(s)ds где 0 < C - const              tо

Если на оценку влияет величина

t

к

t exp —J Л( s) ds к £ a       J

t ₀ + a(£ ) < t < T - a(£) _a(_£)^o оценка (6) верна для отрезки ⁰ , ^{а ( £ )} ^ , Второе приближения определяется следующим образом:

£ ^ 0 и £ = О ( а ( £ ) ) .

t                          It x2 (t, £) = Xj (t, £) + j Xj (t, £)exp ~^Л(s)ds dr

'0              к ^£ T         J

t

’ 0

t

к

Здесь

t

t

к

t

т

к

т

к

J X j ( т, £ ) exp ~^Л(s ) ds dr = M^ x ⁰ ( £ ) exp — J Л ( s ) ds + exp ~^Л(s ) ds t 0               к ^£ T          j          t 0              к ^£ t 0          J       к^£ a          J

X

t 0

t 0

к

t 0

J

t

x exp -J Л ( s ) ds d r к ^£ T        J

.

Отсюда

t

T

к

t

к

M J x ^{0 ( £ ) e}xp £ J ^{л (} s ) ds exp H J ^{л (} s ) dsy = x

t

t 0                  к

t

^f 0              J

t

к

T

J

( £ ) M exp —J Л ( s ) ds ( t - 1 ₀)

к

t 0              J

,

t

а также

к

т

к

к

П Т                                    [у¹.

J exp -| Л ( s ) ds exp -| Л ( s ) ds d r = M exp -| л ( s ) ds ( t - 1 ₀)

t 0     к £ a        J к £ T        j            к £ a        J

t

t

t

t

' 0

Тогда

|x ₂ ( t , £ )| <  C £ exp

u^t^ i1 + M ( t - 1 ₀ ) ] + M exp [ u ^ t ^ t ⁰^ \t - 1 ₀ ) к £ J                    к £ J

При ⁿ = ³ имеем

t

t

к

r                    1 r x3 (t, £) = x (t, £) + j x2 (t, £) exp — j Л( s) ds

/>              к ^£ T         J

d r

Получаем

|x ₃ ( t , £ )| <  C £ exp Г u ⁽ t , t ⁰) 'I 1 + m ( t - 1 ₀ ) + M— ( t - 1 ₀ ) ² к £ Jк                2          J

M2

⁺ y^e xP

;

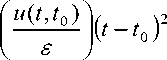
Аналогично xn (t, £) = X

t                              I t

i ( t , £ ) + | X n St, £ )exp -| Л ( s ) ds

'0                 к ^£ T

t

' 0

t

d i

J

Получим

|Xn ( t , s )| <  C s exp

u ( t , 1 0 ) s

1 + M ⁽ t - t 0 ) +— -( t ^- t 0 ^{) 2}

V               2

+ ... +

M^ ( t - ' 0 ) ^{n - 1 ( n} - 1)!

+

x n + 1

+

M^{n -1} ( - - 1 ) ^exp

Или

² и(^\ -1 0 ) n ^-1

V ^s 7

I x_n (t , s )| <  C s exp

" u ⁽ t , t 0 ) ²

V s 7

exp ( M ( t - 1 ₀)) +

Mn -1

L n -1

Докажем справедливости оценки для ^{n + 1}  . Тогда из

t

\

t

( t , s ) = X ( s )exp -p( 5 ) ds +j

s:

V    t 0            7     t 0

t

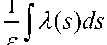
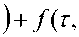
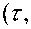
T

имеем

V

,

V

I X n + 1 ( t , s )| <  C s exp ² u ⁽ t , t ⁰) ] exp ⁽ M ⁽ t - 1 0 )) + M — exp ( u^ta 7 - 1 0 )

V s J                   n ! V s J

Последовательные приближения равномерно ограничены:

V n e N ■ x n ⁽ t , ^s ) <  ^C l ^x 11

Докажем

сходимости

{xn(t,s)}

Xn (t, s) = X! (t, s) + (x 2 (t, s) - X! (t, s))+(x 3 (t, s) - X 2 (t, s))+... + (Xn (t, s) - Xn 4 (t, s))

( 4 ) ^

t

Xn (t, s) - Xn -1(t, s) = J exp t 0

t

1 J Ж s ) ds f (

V^ t        7

^T , ^X n - 1

( ^T , ^s )) ^{- f (} T ^X n - 2^{( T} , ^{s ) )]} d ^T

Тогда

I X ₁ ( t , s ) - X ₀ ( t , s )| <  C|x J

I X 2 ( t , s ) - X j ( t , s )| <  C ²1 X 1I

I X з ( t , s ) - X 2 ( t , s )| <  C ³| x J

I ^X n ⁽ t , ^s ) - ^X n - 1⁽ t , ^s )| <  Cⁿ|^X 1|

По модулю

I X j ( t , s ) + ( X 2 ( t , s ) - X j ( t , s ) ) + ( X 3 ( t , s ) - X 2 ( t , s ) ). .. + ( X n ( t , s ) - X n - ( t , s ) ) + ..| <                ⁽⁷⁾

< X ( t , s )| + | x ₂ ( t , s ) - X j ( t , s )| + | x 3 ( t , s ) - X ₂ ( t , s )| + ... + x_n ( t , s ) - X_n - 1 ( t , s + ... <

< |xj|[1 + C + C2 +... + Cn-1 ]

Правая часть равенство (7):

Ix |(1 - Cn+1)

1 - C

I ^X n ⁽ t , ^s )| <

x

< Cx

1 - C ^{1 11}

|x ⁽ t , ^s )| <

.

Методом от противного докажем единственности решения. Пусть существует другое решения задачи (4):

t

\

t

t

xn

y ( t , s ): y ( t , s ) = x⁰

t

( s )exp ¹ j l ( s ) ds + jexp ¹ | д s ) ds • [ ^ ( t - a ) + f ( t , y ( t , s )) ] d

I st        J  t0    I ST        7

к

t 0

t 0

t

\

⁽ t , ^{s )} - y ⁽ t , ^s ) = j ^ex p ¹ j A ^(s ) ^ds \ ^f ( 1 0      к ^S T         7

■ 0

t , X n - J ( t , s ) - f ( t , y ( t , s ) ] d t

,

t

t

T

.

здесь

Тогда

X n ( t , s ) = x/t , s ) + j exp -j A (s ) ds f ( t , x_n ^( т , s )) d T 1 0      к ^s t         7

.

|^X 1⁽ t , ^s ) ^- y ⁽ t , ^s )| <

t

J exp t 0

Л 1Re _к s

t

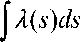
t         7

• |x0(t, s) - y(t, s)|dT <

C|xJ

|^x 2⁽ t , ^s ) ^- y ⁽ t , ^s )| <

t

J exp t 0

t

|^x n ( t , ^{s ) -} y ⁽ t , ^s )| <

1Re

к

s

t          7j A(s)ds • x (t, s) - y(t, s)|dT < C2|xj

T        7

t

\

j exp 1 Re jЛ(s)ds • |x„_4 (t, s) - y(t, s)|dT < Cn^ t0    кs T        J

■ 0

.

Здесь выполняется ^ ^{n e} N (8). Тогда в области

H 0.

lim Cⁿ\x = 0 n ^^

Из равенства (8) при n ^X ^  |x(^s)  y(^s)|  0 . _._ , x(t,s)  y(t,s) , Теорема доказано.

Пример. ^ ⁽ t ) = t ⁺ i , ^ ⁽ t ^- a ) , a >  ⁰ . Тогда условия U2 выполняется и для решения задачи (1)–(2) верно оценка (3).

Результаты и обсуждение

Когда неоднородность это сингулярная функции Дирака, тогда решение задачи оценивается в действительной области. Здесь второе слагаемое равенство (4) вычисляется за счет функции Дирака. Поэтому появится возможность оценивать решение задачи (1), (2) в действительной области. А также можно выбрать затягивания потери устойчивости достаточно большим.

Выводы

Используя свойства сингулярной функции Дирака можно оценивать решение задачи (1)(2) в действительной области. Этот случай особенный, потому что неоднородность обобщенная функция. С обыкновенными неоднородными частями исследовано в работах [13].