Моделирование адаптации костной ткани к новым нагрузкам, возникающим после контролируемого остеосинтеза шейки бедра, осуществлено авторами в предположении одноосного напряженно-деформированного состояния (НДС) [1]. При этом рассматриваемая область была представлена набором цилиндров, расположенных вдоль оси шейки. Данная модель не позволяет учесть влияние таких факторов, как особенность индивидуальной формы и размеров, пространственной неоднородности распределения структурных и механических свойств в костной ткани проксимального отдела бедра пациента, а также вида перелома и ориентации фиксаторов в кости на индивидуальные величины моментов закручивания фиксаторов.

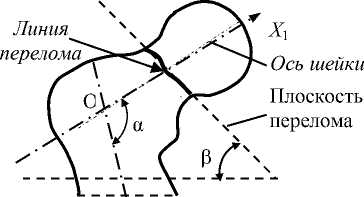
Индивидуальность формы характеризуется в том числе и величиной шеечнодиафизарного угла а (рис. 1, а ), а вид перелома определяется ориентацией плоскости перелома по отношению к анатомическим осям X_P i = 1 , 3 и местом (локализацией) перелома в области шейки (рис. 1, б ).

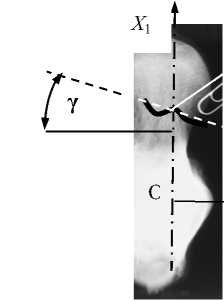
С позиции биомеханики фиксации необходимо знать положение плоскости перелома по отношению к оси шейки как преимущественному направлению равнодействующей сжимающих сил фиксаторов. Из достаточно большого числа реальных ориентаций плоскости перелома обычно рассматриваются два ее предельных положения, представленных на стандартных рентгенограммах своими проекциями в виде прямых линий (см. рис. 1, а , 2, а ). Предельные положения плоскости перелома определяются двумя углами: 1) традиционно углом Pauwels ’а между линией перелома и горизонтальной осью в = 50...70 ° [11] на фронтальной проекции (см. рис. 1, а ) и 2) углом у на боковой рентгенографической проекции проксимального отдела бедра (см. рис. 2, а ).

В первом предельном случае расположения плоскости перелома (см. рис. 1, а ) в силу анатомического строения проксимального отдела бедра ( а = 135 ° ) путем выбора величины угла 5 (см. рис. 1, б) хирург имеет возможность при любом угле в установить фиксаторы под углом к плоскости перелома близким к 90 ° . Это позволяет сжать фрагменты кости практически полной осевой силой фиксаторов и обеспечить абсолютную стабильность фиксации отломков (в случае абсолютной фиксации относительные перемещения контактирующих частиц кости, расположенных на поверхностях щели перелома, равны нулю) [8]. Усилие сжатия губчатой кости одним резьбовым фиксатором, ограниченное при контролируемом остеосинтезе прочностью на срез костной ткани, достигает внушительной величины порядка 650–850 Н [1].

а

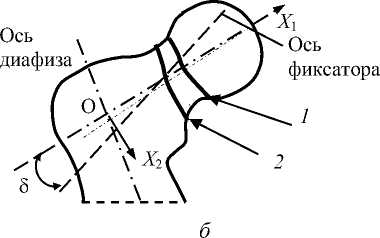
Рис. 1. Углы, характеризующие форму проксимального отдела бедра (шеечнодиафизарный угол α) и ориентацию щели перелома (угол Pauwels ’а β [11] между линией перелома и горизонтальной осью) ( а ), а также области расположения щели перелома в шейке ( б ): 1 – субкапитальный перелом; 2 – трансцервикальный перелом [8]

Линия перелома

Плоскость перелома

X 3

а

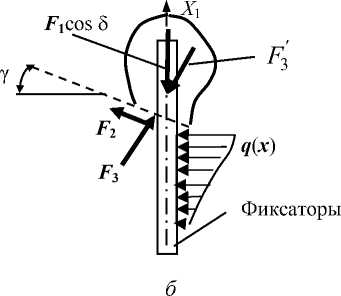
Рис. 2. Угол у на боковой проекции проксимального отдела бедра ( а ) и схема сил, действующих на проксимальный отломок кости после установки фиксаторов ( б ): F 1 – сжимающее усилие фиксаторов; F 2 , F 3 – тангенциальная и нормальная составляющие реакции дистального отломка соответственно; F ₃ ^' – сила сжатия

отломков; q ( x ) – интенсивность распределенной нагрузки, действующей на фиксаторы со стороны дистального отломка кости

Обычно устанавливаются три резьбовых фиксатора. Такая фиксация является необходимым условием прямого заживления перелома шейки бедра как единственного варианта репаративной регенерации данной области, обеспечивающего сращение отломков практически без укорочения шейки [14]. При прямом заживлении перелома сращение костных отломков осуществляется по типу ремоделирования области перелома, когда отсутствует резорбция поверхностей перелома и костная мозоль и отломки кости соединяются остеонами как шипами [14].

Во втором предельном случае расположения плоскости перелома (см. рис. 2, а ) возможности хирурга по установке фиксаторов в направлении, перпендикулярном плоскости перелома, существенно ограничены, и оценка усилия сжатия фрагментов кости, противоположного по направлению и равного по модулю реакции F 3 , определяется как результат двойного проецирования F 3 = F 1 • cos 5- cos y (рис. 2, б ).

При пониженных значениях суммарной осевой силы фиксаторов F , например, когда низка прочность костной ткани пациента, величина силы F ₃ , на первый взгляд, может оказаться недостаточной, чтобы обеспечить абсолютную стабильность фиксации отломков и сращение перелома. Однако клинический опыт [2] показал, что у всех пациентов, оперированных методом контролируемого остеосинтеза, рентгенологически наблюдалось прямое сращение перелома, в том числе и в случаях изменения угла γ в интервале от ± 20 ° до ± 25 ° и пониженных значениях плотности костной ткани головки и шейки бедра порядка 1,18–1,27 г/см³. Данные наблюдения объясняются повышенным коэффициентом трения между отломками и действием фиксаторов, препятствующим относительным перемещениям отломков в плоскости перелома (см. рис. 2, б ). Кроме того, клинические исследования [2] показали, что прямое сращение перелома имеет место при любой локализации перелома.

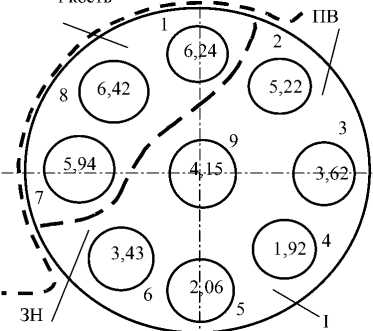
Как показали экспериментальные исследования, поле разрушающих касательных напряжений в костной ткани головки бедра имеет существенную неоднородность [3]. Наибольшей прочностью на срез обладают участки головки, расположенные в зоне контакта головки с тазовой костью, т.е. ее задневерхние участки (ЗВ), воспринимающие контактное давление от веса тела и усилий мышц, а наименьшей – передненижние участки (ПН) головки (рис. 3, а ).

Тазовая кость

ЗВ

ПН

а                               б                               в

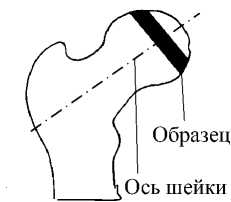
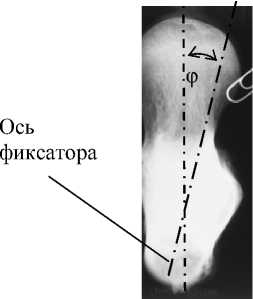
Рис. 3. Биомеханические аспекты головки бедренной кости: а – распределение средних разрушающих касательных напряжений у вершин резьбы фиксаторов (МПа) в четырех дисках-образцах толщиной 5 мм, вырезанных из четырех головок бедра [3]; б – ориентация образца в головке бедра при вертикальной позе человека определяется расположением его четырех условных зон: ПВ - передневерхняя, ПН - передненижняя, ЗВ - задневерхняя, ЗН - задненижняя. 1 - 9 - номера областей выдавливания в опытах. Граница области наибольшей прочности при сдвиге обозначена длинным пунктиром, а дуга контакта головки с тазовой костью – коротким пунктиром; в – ориентация оси фиксатора по отношению к оси шейки бедра на боковой проекции рентгенограммы определяется углом ϕ

Поскольку при установке фиксаторы могут быть введены в любую зону головки, то для выполнения условия прочности костной ткани необходимо определение предельного момента закручивания каждого фиксатора в отдельности. Учитывая, что ориентация оси фиксатора в кости задается углами δ (см. рис. 1, б ) и ϕ (рис. 3, б ), контролируемыми в течение операции, введем эти величины в число исследуемых факторов.

Следовательно, значения углов δ и ϕ , особенность индивидуальной формы и размеров проксимального отдела бедра, а также пространственной неоднородности распределения структурных и механических свойств костной ткани проксимального отдела бедра пациента являются факторами, влияние которых на величину индивидуального момента закручивания каждого фиксатора следует оценить в дальнейшем и представить в последующих сообщениях.

Установление закономерностей влияния этих факторов позволит травматологам обосновать выбор индивидуальной хирургической тактики лечения перелома, что определяет актуальность проблемы исследования.

Методика вычисления величины момента закручивания фиксаторов для контролируемого остеосинтеза перелома шейки бедра включает следующие основные этапы [1]:

• 1)    построение и визуализация проксимального отдела бедра как области исследования;

• 2)    определение поля равновесных деформаций в проксимальном отделе бедра, наблюдаемых при неизменных пиковых значениях функциональных нагрузок на тазобедренный сустав в течение одноопорной фазы шага в норме;

• 3)    определение значения индивидуального момента закручивания фиксатора как предельной по условию прочности костной ткани величины. Прочность костной ткани оценивается как при установке фиксаторов, так и в течение периода сращения перелома, когда осуществляется адаптация костной ткани к изменившимся нагрузкам.

На втором этапе решается квазистатическая линейная задача теории упругости для проксимального отдела бедра при наибольших значениях усилий мышц и реакции тазовой кости, вычисленных оптимизационным методом [15].

На третьем этапе реализуется начально-краевая задача структурной адаптации упругой губчатой костной ткани проксимального отдела бедра, нагруженного сжимающими усилиями фиксаторов, давлением тазовой кости на головку бедра и усилиями мышц, необходимых для иммобилизации больной конечности при ходьбе на костылях [7].

В силу специфики и малого опыта решения подобного рода задач основным и наиболее сложным является третий этап. В связи с этим целью настоящей публикации является математическая формулировка начально-краевой задачи третьего этапа.

К элементам новизны данной формулировки относятся: 1) пространственное представление индивидуальных геометрических, структурных и механических свойств в исследуемой области (проксимальный отдел бедра); 2) различные ориентации расположения фиксаторов в кости, позволяющие определить величину предельного момента закручивания каждого фиксатора и, следовательно, повысить качество фиксации при реализации этих величин момента закручивания в процессе остеосинтеза.

Постановка начально-краевой задачи

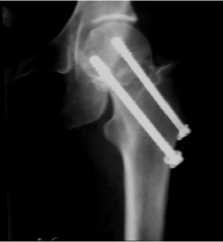
При переломе шейки бедра и последующей операции остеосинтеза больной в течение периода сращения отломков (5-6 месяцев) передвигается на костылях, не опираясь на больную конечность. Конфигурация костей тазобедренного сустава в текущий момент периода сращения представлена на рентгенограмме (рис. 4, а ).

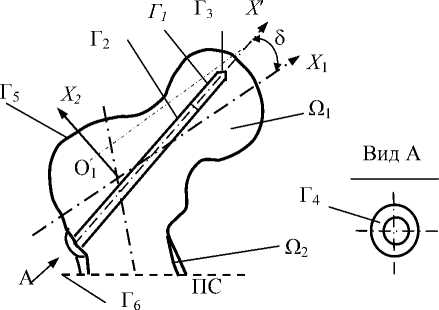
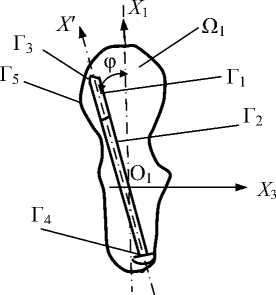
В качестве исследуемой области принимаем проксимальный отдел бедра, ограниченный со стороны дистального конца плоскостью поперечного сечения (ПС) и содержащий два (или три) стандартных резьбовых фиксатора (рис. 4, б ), условно представленные одним фиксатором (рис. 5).

Далее используются следующие основные допущения:

• 1)    процессы транспорта внутритканевой жидкости, деминерализации матрикса, адаптации кортикальной костной ткани и сращения не учитываются;

• 2)    поскольку при контролируемом остеосинтезе всегда реализуется прямое сращение и отсутствуют относительные перемещения отломков, щель перелома в рассматриваемой области отсутствует (см. рис. 5);

• 3)    фиксаторы являются абсолютно твердыми телами, так как модуль упругости стали фиксаторов существенно выше модуля упругости губчатой костной ткани (на два порядка);

• 4)    поры губчатой костной ткани имеют форму сфер.

  

  а

  
  
  
  
  

  б

  
  

Рис. 4. Остеосинтез перелома шейки бедра левой ноги двумя резьбовыми фиксаторами: а – конфигурация во фронтальной проекции костей тазобедренного сустава в период сращения; б – стандартный резьбовой фиксатор длиной 100 мм

а

б

Рис. 5. Исследуемая область Ω губчатой Ω 1 и кортикальной Ω 2 костной ткани

(Q = Q 1 uQ 2 ) с фиксатором во фронтальной ( а ) и боковой ( б ) проекциях.

Г i , i = 1,3 - внутренние и Г i , i = 4, 6 - внешние границы области Q

Для описания структуры губчатой костной ткани используется двухуровневая модель: пористый матрикс и активные костные клетки, расположенные на остеогенных поверхностях пор. Параметрами структуры представительного объема костной ткани являются радиус пор r ( X, t ) и плотность пор n ( r ) как функции радиус-вектора частицы X и времени t . Радиус пор относится к независимым параметрам, а плотность пор выражается через плотности сырой костной ткани р _ск ( r ) , матрикса (вещества кости) р м , плотность костного мозга в порах р _км и радиус пор посредством равенства [5]

n ( r ) = 1 -

V

Р ск ( r ) — Р км ) 3

Р м -Р км   ) ^{4 п r 3}’

где функция р _ск ( r ) определяется по экспериментальным данным [4].

Система уравнений начально-краевой задачи включает следующие соотношения, записанные для текущего момента сращения t е ( 0, T ] (все тензорные величины и их инварианты, входящие в эти соотношения, являются также функциями радиус-вектора частицы X и времени t ):

• -    уравнение равновесия **

V^d + Рск (r) g = 0, X е^ = Ц ^^2, где g - ускорение свободного падения;

• -    кинематическое соотношение Коши для тензора малых деформаций

£ = 1)2 (V и + *7), X еП,(3)

где V - оператор Гамильтона; и - вектор перемещения;

• -    определяющее соотношение адаптационной пороупругости Cowin’ а [12] запишем в виде

  
  
  

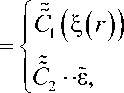
  x efl , ,

  x e Q 2 ,

  
  
  
  

^v где C1 (£(r)) - тензор жесткости губчатой костной ткани - является функцией объемного содержания матрикса £( r), определяемой экспериментально и удовлетворяющей условию

/ч/ w

S ( r ) = 0

= 0,

а C ₂ – тензор жесткости кортикальной костной ткани бедра – принимается постоянным.

Для губчатой костной ткани как изотропной среды компоненты тензора ^w

C 1 ( £ ( r ) ) определяются модулем упругости E и коэффициентом Пуассона v. С помощью решения обратной задачи теории упругости, сформулированной для модели образца влажной губчатой костной ткани, имеющего реальную структуру, получена зависимость модуля упругости от объемного содержания матрикса [13]

E (^( r )) = Em ^( r )L7,                                    (6)

где E_m - модуль упругости матрикса, а зависимость £ ( r ) имеет вид [4]

£ ( ^r ) = ^{1 -} 3 ^п n ( ^r ) ^r •                                     ⁽⁷⁾

Для коэффициента Пуассона зависимость от объемного содержания матрикса в настоящее время не установлена. В связи с этим принимаем величину ν постоянной, что позволяет с учетом (6) удовлетворить условию (5);

• -    кинетическое уравнение структурной адаптации губчатой костной ткани устанавливает связь скорости изменения параметров структуры (радиуса пор) с активностью костных клеток и деформационным стимулом адаптации [6]

r ( I . , r ) = - af ( r ) sgn ( I eq )( I . - I eq ) ,                           (8)

где I _E , I e - первые инварианты тензора деформации в актуальной и в равновесной конфигурациях соответственно – являются функциями времени, а положительная функция f ( r ) определяется соотношением

f ( Г ) = Sv ( r ) /

Sv ( r ) +

³ ( р ск ( ^r ) ^-Р м ) / ^{r -д}Р ск ( r )/ 5 ^r Р м —Р ж

где Sv - суммарная в единице объема костной ткани площадь поверхности пор (мм2/мм3). Коэффициент a зависит от активности и плотности расположения костных клеток на поверхности Sv и вычисляется по формуле ab ^ b + ac ^ c > 0 max min

где X _b , X c - доли поверхности пор, занятой остеобластами или остеокластами соответственно; a_b , a_c – скорости производства и резорбции матрикса соответственно (мм/день); к max , г min - границы интервала изменения деформации, стимулирующей адаптацию ( ± 0,3 % [9]). Согласно вычислениям по известным экспериментальным данным для губчатой костной ткани а = 55 мкм/(день ∙ ЕОД), здесь ЕОД – единиц относительной деформации [9].

Соотношение (8) описывает как резорбцию, так и производство клетками костного вещества в зависимости от характера и величины изменения объемной деформации костной ткани, обусловленные действием имплантатов. Процесс адаптации запускается, если абсолютная величина разности I _к - 1 K q превышает половину ширины зоны адаптационной нечувствительности костной ткани (величина порядка 0,0005), в противном случае адаптация отсутс тву ет;

• -    граничные условия на границах Г i , i = 1,4 (см. рис. 5) формулируются исходя из допущения о фиксаторах как абсолютно твердых телах, действие которых на костную ткань учитывается в соответствии с принципом освобождаемости от связей.

• 6. e' = - — e ' , X _€Г 1 , (11) S _b

Со стороны резьбы фиксатора, закрученного моментом M , на костную ткань действует равномерно распределенная нагрузка F ( t ) /S b , где F ( t ) - осевая сила фиксатора, а S_b - площадь опорной поверхности резьбы. Следовательно, на цилиндрической границе кости Г 1 необходимо выполнение условия

F _

где е ' - орт оси фиксатора X' в системе координат Xi , i = 1, 2, 3 - представим в виде функции углов 5 , ф , определяющих, соответственно, направление фиксатора по отношению к координатным плоскостям X 1 X 3 и X 1 X 2 (см. рис. 5),

e'(5. ф) = Е 3=1 ni (5, Ф) ei,

-

где e i , i = 1 , 3

в соответствии координат

орты осей Xi, i = 1,3, а направляющие косинусы ni (5, ф), i = 1,3, с правилом двойного проецирования вектора в прямоугольной системе

n1 (5, ф) = cosP(5, ф) cos5, n2 (5, ф) = cosp(5, ф) sin5, n3 (5, ф) = sinp(5, ф),

где в

-

угол

между вектором

e' и плоскостью XX 2 как функция углов 5 , ф

определяется соотношением

tg P = cos 5- tg ф

.

Аналогично со стороны

головки фиксатора на кость действует также равномерно распределенная нагрузка F (t) / S4, где S4 - площадь кольцевой границы

Г 4 (вид А на рис. 5, а ). Следовательно, напряжения в костной ткани должны удовлетворять равенству

F ^{e      e    e}

• 6. e = —e ,  x еГ₄ .

S 4              ⁴

Поскольку острие фиксатора не касается кости на границе Г3, т.е. поверхность кости на данной границе свободна от нагрузки (это же относится к поверхности кости на границе Г5), то соответствующие силовые граничные условия запишем в виде d • n (x ) = 0, x eFi, i — 3,5,(16)

где n_i - орты внешних нормалей на границах Г _{3, 5} .

На границах контакта кости и фиксаторов выполняются условия непроникновения частиц кости в металл u (x )• n (x )< 0, x e ri, i — 1,4.(17)

Граница Г6 фиксируется так, что одна из ее точек (С) закреплена в глобальной системе координат Xi, i = 1, 2, 3, u (xc ) = 0, xc e Г6,(18)

а остальные точки закреплены только в направлении нормали

1l(x\-°(x\-^ °<=V /° u \x i n yx I — v, x e l 6 / xc ;(•*•'')

• - начальные условия фиксируются в момент окончания установки фиксаторов и определяются значениями следующих величин:

• •    осевой силы сжатия костной ткани одним фиксатором, закрученным моментом M

  F ( ⁰ ) =

  
  

  м - м р f г k_d + 0 , ⁵ d 2 tg ( ф + ф ) ,

  
  
  
  

где M _р - момент затирания вершин витков резьбы фиксатора в неполной резьбе, созданной метчиком; f _г - коэффициент трения между полированными стальными поверхностями головки фиксатора и шайбы; k_d - коэффициент, определяемый характерными диаметрами резьбы, в том числе средним диаметром d ₂ ; у , Ф - углы подъема резьбы и трения в резьбе соответственно [10]. Соотношение (20) получено из условия предельного равновесия моментов сил трения в резьбе и головке и момента закручивания M ;

• •    радиуса пор

r ₀ ( x ) — r ( .°, 0 ) , x e Q 1 ;

• •    компонент тензора жесткости губчатой костной ткани, вычисляемых с помощью соотношений (6), (7),

C ₁₀ ( x ) — C 1 ( x, 0 ) , x eQ 1 .                              (22)

Соотношения (1)–(22) содержат замкнутую систему уравнений (2)–(5) начальнокраевой задачи с граничными (11), (15)–(19) и начальными (20)–(22) условиями и позволяют определить адаптационное изменение свойств костной ткани после закручивания каждого фиксатора в заданном направлении и с заданным моментом.

Как отмечалось выше, максимальное значение момента закручивания каждого фиксатора ограничивается прочностью костной ткани на срез у вершин резьбы фиксаторов. Следовательно, напряжение на границе Г 1 ограничивается величиной касательного напряжения разрушения т * ( r ( ° , t ) ) :

• 72                       ISSN 1812-5123. Российский журнал биомеханики. 2013. Т. 17, № 2 (60): 64–74

  | d • e

  
  

  kH x ojl

  
  

  k T

  
  

  x e Г 1 ,

  
  
  
  

где k _T - коэффициент запаса прочности - мы принимаем постоянной величиной, близкой к единице (порядка 1,2-1,3), поскольку нагрузка стационарна. Функция т * ( r ( х, t )) получена на основании экспериментальных данных [3, 4] и имеет вид

т * ( r ( х, t ) ) = 30,556 r ( х, t ) - 15,196,

здесь радиус пор r ( х, t ) измеряется в миллиметрах и, как функция времени, находится интегрированием соотношения (8).

Заключение

Данная статья (сообщение 1) посвящена проблеме влияния как механических, так и хирургических факторов на величины предельных моментов закручивания фиксаторов при контролируемом остеосинтезе перелома шейки бедра. Осуществлен анализ значимости различных хирургических факторов, на основании которого влияние направления оси каждого фиксатора принимается в качестве наиболее важного фактора, тогда как ориентация плоскости перелома (по Гардену) и ее локализация не влияют на величину предельных моментов закручивания фиксаторов. Представленная в соотношениях (1)–(23) математическая модель начально-краевой задачи структурной адаптации губчатой костной ткани проксимального отдела бедра ориентирована на пациента, поскольку содержит такие характеристики, как радиус пор и плотность, измеряемые перед операцией индивидуально. В сообщениях 2 и 3 эта модель будет использована для определения влияния формы проксимального отдела бедра, пространственной неоднородности распределения структурных и механических свойств костной ткани, а также направления фиксаторов в кости на величину предельных по прочности кости моментов закручивания фиксаторов.