Влияние геометрических параметров соплового устройства и времени истечения жидкости на кинетическую энергию жидкого снаряда

Данная статья является продолжением исследования рабочего процесса эжектора с прерывистой струей. Ранее было рассмотрено влияние времени истечения жидкости через сопло на относительную скорость формируемого снаряда, определены закономерности изменения скорости на срезе и зависимости скорости от времени открытия сопла [1–8]. Разработанная методика определения оптимального времени истечения жидкости через сопло отражает только одну составляющую кинетической энергии – скорость, получаемую снарядом в фазе разгона [9, 10].

При формировании снаряда главную роль играет кинетическая энергия, передаваемая от активного потока снаряду, благодаря которой снаряд выполняет работу по сжатию газа или жидкости пассивной среды. При этом надо полагать, что, если энергия будет недостаточной для совершения работы, снаряд остановится в рабочей камере и произойдет сбой в работе эжектора [11]. Если энергия будет больше необходимой для совершения работы, то ее излишки будут гаситься в отводящем трубопроводе, что приведет к дополнительным потерям энергии и снижению КПД. Поэтому для повышения эффективности эжектора с прерывистой струей необходима методика для определения оптимального времени истечения жидкости через сопло в зависимости от необходимой энергии снаряда, зависящей от параметров, в которых работает эжектор [12, 13].

Расчетная модель соплового блока

Уравнение энергии, предаваемой снаряду от активного потока:

с _ т ∙ V² кин = о

где т – масса жидкого снаряда; v – мгновенная скорость снаряда в конце фазы разгона.

Как видно из уравнения, увеличение кинетической энергии на промежутке времени от 0 до достижения стационарной скорости истечения будет наибольшим ввиду увеличения массы и скорости одновременно, а после выхода на стационарную скорость увеличивается только масса и зависимость становится линейной [14].

Мгновенная скорость потока при нестационарном течении от времени открытия определяется по следующей зависимости:

V =

(Y^ ∙(i+(с⁾ к 2∙ 1с

∙t

Поскольку истечение активного потока является нестационарным течением, масса жидкого снаряда может быть определена по следующему выражению:

т = ж ^∙ ш с ∙∫ ydt ^,

где р _ж – плотность рабочей жидкости активного потока [15]; а> _с – площадь сопла на срезе [16].

Подставляя в это уравнение мгновенную скорость и интегрируя ее по времени, при начальных условиях t 0 = 0; V 0 = 0, получаем

=

2 ^∙ к ^∙ " с ∙ Р ж

1+?с

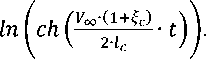
Уравнение энергии, предаваемой снаряду от активного потока, приобретает вид

F. = кин

К» ^∙ к ^∙ " с ∙ р ж

1+(с

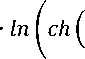
Voo ∙( ш с⁾

2∙ 1с

^∙О^∙ ‘^ℎ2(- ∙( _∙ с ) _∙ о^.

Полученная аналитическая зависимость кинетической энергии снаряда при нестационарном течении от времени открытия задвижки позволяет рассчитать необходимое время истечения жидкости через сопло и для совершения этим снарядом работы по сжатию газа и преодоления сил сопротивления [17–21].

Результаты и обсуждения

На рис. 1, 2 приведены зависимости кинетической энергии снаряда от времени истечения жидкости через сопло при значении коэффициента сопротивления сопла f с=0,05, перепадах давления 100; 200; 300 и 400 кПа и инерционных длинах 0,1; 0,3; 0,5 и 1 м.

Анализ полученных графических зависимостей (см. рис. 1–4) показывает, что с увеличением инерционной длины при одном и том же давлении графики зависимости кинетической энергии от времени становятся более пологими. Это означает, что с увеличением инерционной длины замедляются темпы прироста кинетической энергии. Соответственно, при увеличении времени истечения через сопло или перепада давления на сопле темп прироста кинетической энергии увеличивается, однако это приводит кувеличению затрачиваемой энергии. При проектировании соплового устройства с прерывистой струей рекомендуется выбирать инерционную длину как можно меньше, что позволит уменьшить энергозатраты и увеличить производительность соплового устройства.

Переход от скорости снаряда к его кинетической энергии позволит, во-первых, упростить выбор времени истечения жидкости через сопло, во-вторых, сократить потери энергии, тем самым повысить КПД. Время истечения жидкости через сопло подбирается таким образом, чтобы кинетическая энергия снаряда была больше или равна суммарной энергию, необходимой для совершения работы по сжатию газа, с учётом потерь энергии в ходе движения и минимальной энергии снаряда, при которой он не потеряет своей индивидуальности. Оптимальная кинетиче- ская энергия снаряда

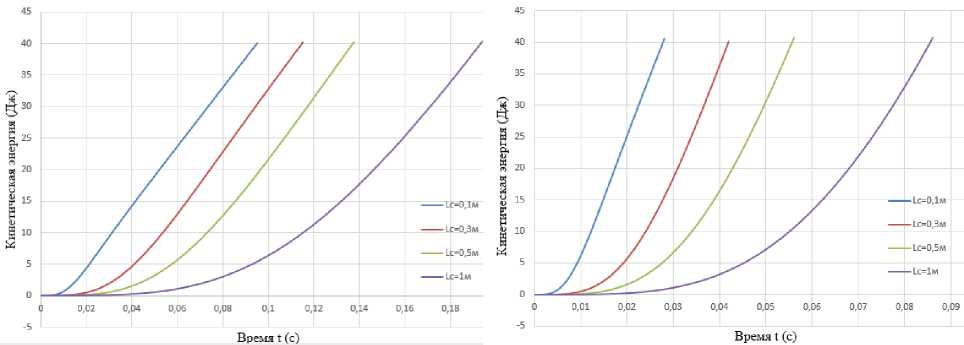
Рис. 1. График зависимости кинетической энергии от времени истечения жидкости через сопло задвижки при 100 и 200 кПа

Fig. 1. Graph of the dependence of the kinetic energy on the time of the liquid flow through the valve nozzle at 100 and 200 kPa

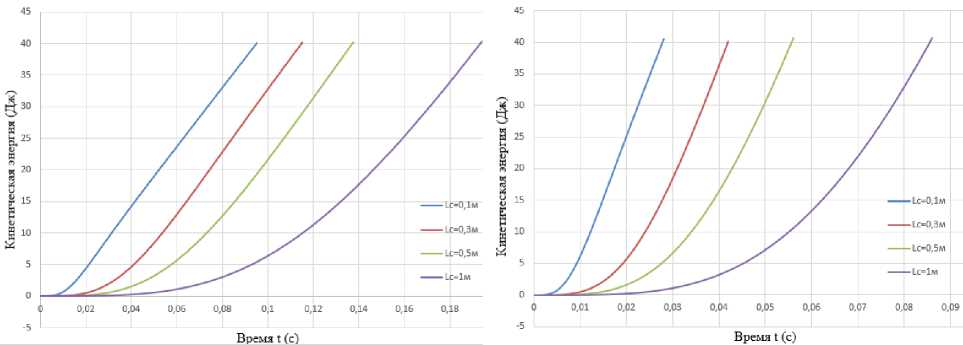
Рис. 2. График зависимости кинетической энергии от времени истечения жидкости через сопло задвижки при 300 и 400 кПа

Fig. 2. Graph of the dependence of the kinetic energy on the time of the liquid flow through the valve nozzle at 300 and 400 kPa

£кин ≥ £необ = A сж E + Eq ,                                                          (6)

где E _кин – кинетическая энергия снаряда; A _сж – работа, необходимая для сжатия газа; Δ E – потери энергии на трение и местные сопротивления; Eq – минимальная энергия, которой должен обладать снаряд, чтобы не потерять свою индивидуальность.

Работу по сжатию газа можем определить по следующей зависимости:

A сж =Δ P52 ^∙<^0 ^∙ ^0 ,                                                                            (7)

где Δ P^2 – перепад давление на рабочей камере; ω Q – площадь сечения рабочей камеры; Iq – длина рабочей камеры.

Потери энергии на трение и местные сопротивления:

Δ E =Δ P пот ∙<^o ^∙ ^o ,                                                                            (8)

где Δ P _пот – потери давления на трение и местные сопротивления.

Минимальная энергия, которой должен обладать снаряд, чтобы не потерять свою индивидуальность, будет получена опытным путем серией экспериментов. В первом приближении минимальную энергию можно принимать равной 20 % от суммы работы и потерь энергии при движении.

Вычислив необходимую энергию снаряда по уравнению (6) с помощью уравнения (5), определяем необходимое время открытия для разных исходных параметров соплового устройства, что позволит наиболее эффективно использовать эжектор с прерывистой струей.

Рассмотрим методику определения оптимального времени истечения для системы со следующими исходными данными: Δ P12 = 250кПа; f с = 0,05; P ж = 1000 кг ; l_c =0,5 м, Δ ⁼ = 90кПа; потери давления примем равными 10 %.

• 1.    Определяется стационарная скорость истечения:

  V DO

  
  

• 2.    Уравнение для определения необходимой энергии:

• 3.    Подставляя полученное уравнение в уравнение (5), получаем

2∙250∙103 Па

=21,82м. с

(1+0,05) ∙1000кг

£необ=1,2∙^0 ∙ "o ∙(ΔP52 +Δpпот) =1,32∙^0 ∙ "0 ∙ΔP52 .

2 ^{, 32} ∙Δ p₅₂ ∙( « с) ₌ ln( c ℎ     ∙( i₊5 с) _∙     ∙tℎ2/^ ∙( « с) _∙

Kxj ∙pж∙n∙Л             \ к 2∙lc                     к2∙

Л с где Ω= с – относительная площадь сопла; Λ= с – относительная длина сопла.

Принимая относительные площадь сопла и длину сопла 0,9 и 0,2 соответственно, решая ито- говое уравнение относительно времени открытия, получаем оптимальное время открытия 0,0964 с. Данная методика позволяет наиболее точно рассчитывать оптимальное время открытия задвижки, в предыдущей статье [1] мы определили, что после 0,9 с изменения скорости практически не происходит, однако дальнейшее исследование процесса показало, что важно учитывать и массу снаряда, что напрямую влияет на его кинетическую энергию.

Заключение

• 1.    В статье рассмотрено влияние основных геометрических параметров соплового устройства на кинетическую энергию, передаваемую снаряду активным потоком.

• 2.    Получена аналитическая зависимость изменения кинетической энергии снаряда с учетом введенных допущений, а именно: жидкость несжимаема, открытие канала происходит мгновенно. Полученная зависимость позволяет рассчитать достаточную кинетическую энергию для совершения работы по сжатию газа с целью повышения эффективности эжектора с прерывистой струей.

• 3.    Получены графики зависимости кинетической энергии от времени открытия сопла, анализ этих графиков показывает, как изменяется кинетическая энергия снаряда в зависимости от инерционной длины, при увеличении которой набор энергии снарядом замедляется, что отражается на КПД эжектора.

• 4.    Получены зависимости необходимой суммарной энергии снаряда, требуемой для совершения работы по сжатию газа, преодоления потерь энергии в ходе движения в рабочей камере и минимальной энергии снаряда, при которой он не потеряет своей индивидуальности.

• 5.    Разработана уточненная методика для определения оптимального времени истечения жидкости через сопло.

Список литература