Влияние геометрической алгебры Древней Греции на развитие математики

Зародившись в глубокой древности из практических и хозяйственных нужд, геометрия была востребована египтянами для восстановления границ земельных участков после регулярных разливов реки Нил, при сооружении оросительных каналов, культовых сооружений, пирамид и т.д. Она развивалась в связи с проведением религиозных обрядов. Священные книги древней и средневековой Индии, Китая содержат сведения о геометрических фигурах и их свойствах, в частности, свойствах правильных многоугольниках. Они повсеместно использовались при построении фундаментов храмов, алтарей, жертвенников, имевших кратные площади и объемы. В связи с этим приобрело актуальность нахождение площадей фигур.

1.    Первые научные школы

Истоки теоретической геометрии относят к естественнонаучным и философским школам Древней Греции. Ведущее место среди них занимала пифагорейская (VI–V вв. до н.э.). Именно в ней происходило накопление абстрактных математических фактов, соеди-

нение их в отдельные системы и создание теоретических основ. В этот же период осуществлялась систематизация геометрических сведений, вводились и совершенствовались приемы доказательства теорем.

Одной из причин создания математических теорий явилось открытие иррациональ ностей. Первая из них – 2 – появилась в геометрии при попытке нахождения общей меры диагонали единичного квадрата и его стороны. Этот факт был логически строго доказан пифагорейцами с использование разработанного метода "приведения к нелепости". Они получили и другие иррациональности, осуществили их первые классификации [1].

Появление иррациональностей в зарождавшейся греческой математике привело к возникновению трудностей как в теоретикочисловом, так и в геометрическом плане: была поставлена под удар метрическая часть геометрии, теория подобия. Пифагорейцы стали искать выход из создавшейся ситуации. Так как оказалось, что множество геометрических величин (отрезков) было более "полным" по сравнению с системой рациональных чисел, в школе стали строить новую теорию на основе геометрических объектов. Она получила название геометрической алгебры .

Основными (неопределяемыми) понятиями ее являлись отрезки, с которыми могли быть осуществлены четыре арифметические операции: сложение, вычитание, умножение и деление. Деление интерпретировалось как эквивалентная задача приложения площадей . В геометрическую алгебру входили и геометрические предложения, касающиеся алгебраических тождеств, таких как ( a ± b )²= a ² ± 2 ab + b ²; a ² - b ² = ( a - b )( a + b ) [2].

Метод приложения площадей был применим при решении задач, сводившихся к решению линейных и квадратных уравнений; определению длины сторон правильных вписанных и описанных многоугольников через диаметры вписанной и описанной окружностей, "золотого сечения" отрезка, выражению длины ребер правильных многогранников через диаметр описанной сферы и др. Задачи такого рода решались с помощью канонического метода, который в зависимости от вида квадратного уравнения имел три разновидности: параболический, эллиптический и гиперболический. Очевидно, что в процессе применения этого метода находился лишь один (положительный) корень соответствующего ему квадратного уравнения. Поэтому греки формулировали условия геометрических задач таким образом, чтобы они имели положительное решение. Для этого в их условие (если требовалось) вводились ограничения (диоризмы) [3].

2.    Методы геометрической алгебры

Исторически сложилось так, что к решению задач, связанных с нахождением площади прямолинейных геометрических фигур, наметились два подхода. Один был основан на понятиях равновеликости и равносоставленности, другой вначале представлял собой последовательность правил для решения задач, а впоследствии оформился как аналитический.

Первый широко применялся уже в Древней Греции. Он назывался методом разложения (разбиения). Суть его заключалась в следующем: для вычисления площади искомой фигуры пытались разбить ее на конечное число частей, так чтобы из них можно было составить другую, более простую, площадь которой могла быть найдена. Там же появились и первые "головоломки". К ним, в частности, относилась игра "стомахион", изобретенная великим Архимедом (280 - 212 гг. до н.э.), в переводе с греческого означавшая "то, что вызывает злость". Название, по-видимому, указывало на трудность, необходимость терпения при составлении любой заданной фигуры. Прямоугольник, длины сторон которого относились как 1:2, разрезали на 14 частей (рис. 1), из которых составлялись различные фигуры (рис. 2, а, б).

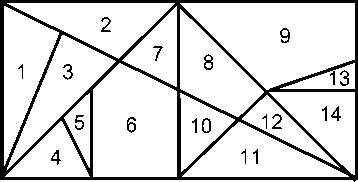
Рис. 1

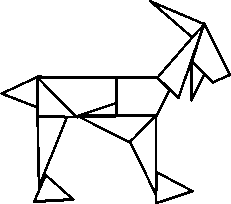
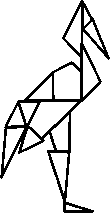
а                  б

Рис. 2

Широкое распространение, особенно на родине своего создателя - китайского ученого Та-нга, получила увлекательная головоломка "танграм". Несколько тысяч лет назад он предложил разрезать квадрат на части (рис.3).

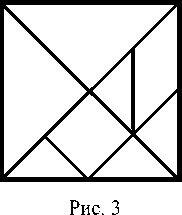
Из всех семи частей квадрата можно составить самые разнообразные фигуры–силуэты (рис. 4, а - в). Популярность игры привела к появлению специальных состязаний на составление наибольшего количе- ства фигур с наименьшими затратами времени.

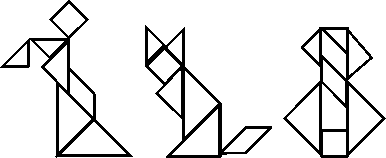
а          б            в

Рис. 4

Победители, как и при древней игре в шахматы, награждались, получали известность.

Используя метод разбиения, искомую фигуру приводили в конечном счете к равновеликому ей квадрату, площадь которого сравнивали с квадратом – эталоном. На рис. 5 и 6 показаны две равносоставленные фигуры – крест и квадрат.

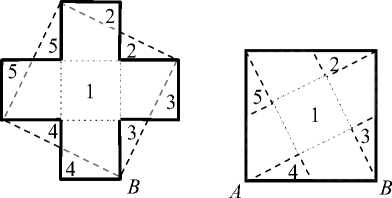
Рис. 5                   Рис. 6

Тогда же в пифагорейской гетерии бы- ли доказаны, в частности, теоремы о равновеликости геометрических фигур: параллелограмма (ромба) и прямоугольника, треуголь- ника и параллелограмма, трапеции и треугольника и др. Заметим, что эти теоремы доказываются аналогичным образом и в совре- менном школьном курсе геометрии. Равновеликость трапеции ABCD и треугольника ABE показана на рис. 7.

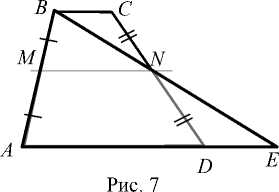
С методом разбиения в Древней

Греции был тесно связан другой способ вычисления площади

– метод дополнения . Он заключался в том, что вместо разрезания фигур на равные части, дополняли рассматриваемые фигуры так, чтобы получившиеся после дополнения фигуры были равны.

Вернемся к рис. 5 и 6. Крест и квадрат имеют одинаковую площадь, так как они равно-составлены. Теперь дополним каждый из них четырьмя равными треугольниками (рис. 8, 9). В результате получится одна и та же фигура. Следовательно, крест и квадрат равновелики.

Метод дополнения был успешно применен для доказательства многих теорем элементарной геометрии. К их числу относилась прежде всего теорема Пифагора. Наиболее раннее ее доказательство было выполнено для равнобедренного прямоугольного треугольника (рис. 10). Под рисунком, как обычно,

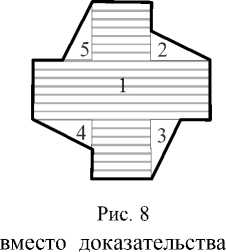
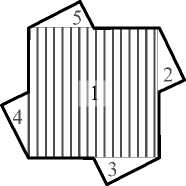
Рис. 9

ная надпись: "Смотри"! Для общего вида прямоугольного треугольника была  доказана теорема в пифагорейской школе, также с использованием метода дополнения.

Пусть АВС (рис.11). Для доказательства того, что площадь  квадрата, построенного на гипотенузе,     равна сумме площадей квадратов, построенных на катетах, обращались к рис. 12, а, б. На них показано, что квадрат 1 и взятые вместе помещалась лаконич-

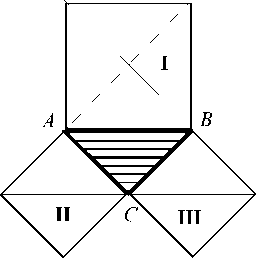
Рис. 10

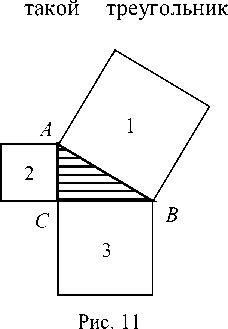
квадраты 2 и 3 можно дополнить четырьмя треугольниками a , b , c и d , равными Δ АВС , до квадрата. Длина стороны каждого из них равна сумме длин катетов треугольника АВС . Тем самым теорема Пифагора доказана [2].

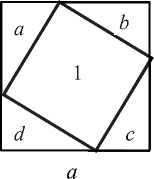
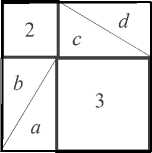
Рис. 12

Заметное место в изучении пифагорейцами свойств геометрических фигур, вычислении их площадей занимало преобразование в равновеликие фигуры. Основой его послужила теорема о равновеликости треугольников с одним и тем же основанием и равными высотами, опущенными на это основание (рис. 13). Ее использовали для преобразования многоугольников (выпуклых и не являющихся таковыми) в равновеликие им треугольники. На рис. 14 и 15 показана процедура преобразования выпуклого и невыпуклого четырехугольников в равновеликие им треугольники.

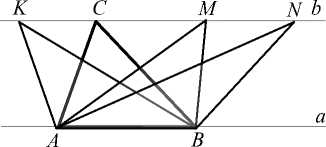
Рис. 13

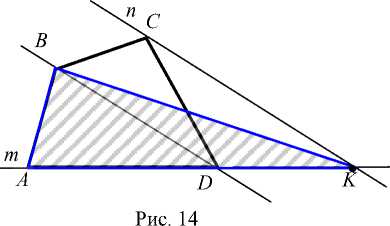
Построение:

• 1.    m : [ AD ] е m ;

• 2.    [ BD ];

• 3.    n : n || [ BD ], C e n ;

• 4.    K = m n n ;

• 5-    [ BK ]. S ABK = S abcd •

В случае невыпуклого четырехугольника теорема применялась к равновеликим треугольникам BDC и BDF .

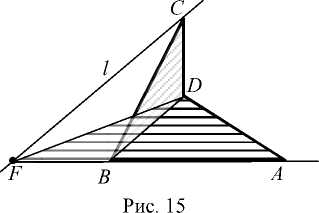
Построение:

• 1. [ BD ];

• 2.    l : 1 1| [ BD ], C e l ;

• 3.    F = AB n l ;

• 4. [ FD ] . aAFD - искомый, так как

S i BDC = ^S i BDF , откуда S ABCD = ^S i AFD .

Заметим, что в некоторых случаях пифагорейцы преобразовывали невыпуклый четырехугольник в равновеликий ему выпуклый, после чего выполняли дальнейшие построения. Так, на рис. 16 четырехугольник ABCD преобразован в выпуклый AEKF после замены двух пар равновеликих треугольников: ECB на ECK и CFD на CFK .

A

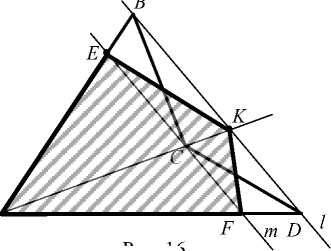
Рис. 16

Построение:

• 1.    [ AC );

• 2.    [ BD ] с l ;

• 3.    m : m || l, C e m ;

• 4.    E = m n [ AB ], F = m n [ AD ], K = [ AC) n l ; 5. EK, KF . S abcd = S aekf .

Аналогичным образом преобразовывались выпуклые 5-, 6- ,..., n -угольники в равновеликие им треугольники, а затем - в прямоугольники и квадраты. Последние сравнивали с эталоном. На рис. 17 показано преобразование шестиугольника ABCDEF в равновеликий ему треугольник МСК .

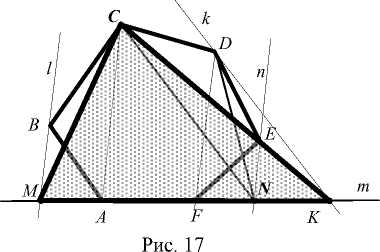
Построение:

• 1.    m : AF с m ;

• 2.    [ AC ], [ FD ];

• 3.    l : l || [ AC ], B e l, n : n || [ FD ], E e n ;

• 4.    М = m n l, N = m n n ;

• 5.    [ CM ], [ DN ], [ CN ];

• 6.    k : k || [ CN ], D e k ;

• 7.    K=k n m ;

• 8.    [ CK ] .

Шестиугольник ABCDEF последовательно преобразовывался в равновеликие ему 5^—, 4^— и 3^—уГ^ольник, поэтому S ABCDEF = ^S MCDEF = = ^S MCDN = S & MCK •

Затем треугольник МСК преобразовывали в равновеликий ему прямоугольник MSTK (рис. 18).

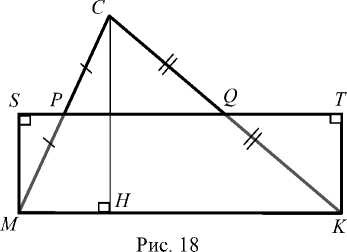
Построение:

• 1.    [ PQ ] — средняя линия М МСН ;

• 2.    [ MS] : [ MS] 1 PQ , S e PQ ;

[ KT] : [ KT] 1 PQ , T e PQ . S mstk = S_Mck •

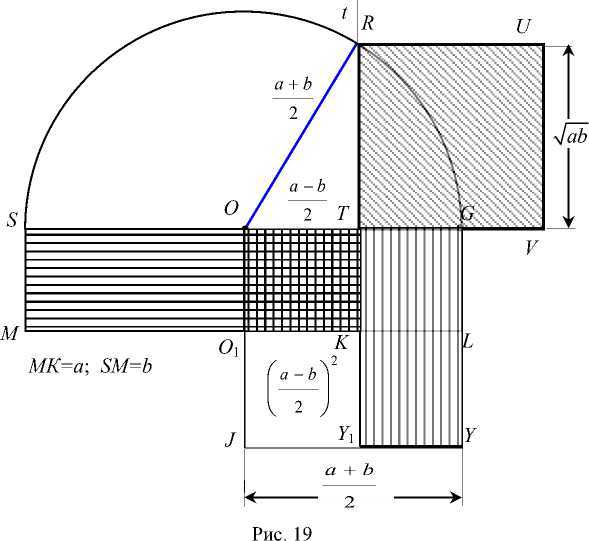
Используя параболический метод приложения площадей, пифагорейцы преобразовывали MSTK в равновеликий ему квадрат (рис. 19). Пусть МК=a, SM= b. Они дополняли прямоугольник MSTK квадратом TGLK. Точкой О делили SG пополам. Тогда SO = OG = a + b         a + b      a - b

----, а OT =-- b =---- . Затем на OG

2             2          2

строили квадрат OGYJ и доказывали, что S STKM , равная ab , равновелика гномону

OGYY i KO i , так как MSTK и последний имеют общую площадь OTKO 1 , а S_SOOiм = S_/(,^ = a + b

=-- b [3].

Дальнейшее построение сводилось к последовательному выполнению операций:

• 1.    а ( O ; SO );

• 2 .    t : 1 1 SG , T e t ;

• 3.    R= a n t ;

TR - сторона искомого квадрата.

Поэтому S _TRUV = S _STMK . Следовательно, S ABCDEF = S TRUV .

В "Началах" Евклида (III в. до н.э.) широко использована геометрическая алгебра. Среди его задач отметим следующие три [4].

• 1.    К двум прямым [отрезкам] найти среднюю пропорциональную. Задача была решена еще в пифагорейской школе с использованием параболического метода приложения площадей.

• 2.    Разделить АВ в точке Н на две части,

чтобы прямоугольник, заключенный между целым отрезком АВ и одной из его частей, был равен квадрату, построенному на другой его части (Предложение XI книги II "Начал" (деление отрезка в отношении "золотого сечения").

Построение: На отрезке АВ Евклид строил квадрат ABCD, точку Е - середину стороны AD - соединил с вершиной B (рис.20) и продолжил DA за точку А так, чтобы EF=BE . На AF построил квадрат AFGH . Наконец, продолжил GH до пересечения с DC

в точке К .

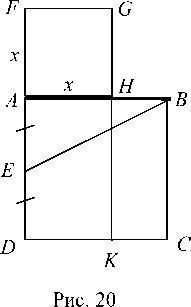
Отрезок AB оказался разделенный точкой Н в соответствии с условием задачи: AH ² = ABBH [4].

Действительно, используя современную символику, обозначим АН = х , АВ = а . Тогда

резке DF построил квадрат DFMK и провел CG || FH . Очевидно, S kabg = х ², а S kdf _H = 196.

НВ = а - х . Так как AE =   , то

FE = x + a = BE . В aBAE BE ² = AB ² + AE²

22 2a2a или x + — + ax = a +--. После упроще- ний получим x2 = a2 – ax , т. е. x2 = a(a – x).

3. "Квадрат, построенный на стороне вписанного [правильного] пятиугольника, равен сумме квадратов сторон вписанных в тот же круг правильных шестиугольника и десятиугольника", (Предложение X книги XIII "Начал").

Евклид предложил геометрическое доказательство задачи, показав справедливость тождества a 2 = a_l 2 + a 2 . Длины сторон а 5 , а 10 и а 6 он выразил через радиус описанной окружности     R :      a ₅ = — 10 — 2141,

K

G

A

x2 48 B 48 y2 x    C y

Рис. 21

D

H

F

Поэтому S KABG + S BCFE = x ²+ y ² = 100. Но 2 xy = 96, следовательно, ( x – y )² = 4, откуда x – y = 2. Учитывая первое уравнение системы, он нашел x =8, y =6 [5].

a ,« = R ( В - 1 )

, a 6 = R , а затем доказал спра-

ведливость тождества [4]. Аналитическое до-

казательство имеет вид

R ² (Ю - 2/5 ) = R ² ( 5 - - 1 ) 2 + R ² = = R - ( б - 2^5 ) + R ².

3. Применение геометрической алгебры

Сведения о геометрической алгебре древних греков проникли в страны арабского халифата, Китай и Индию. Как следует из [7], уже в трактате, относящемуся приблизительно к 1100 гг. до н.э., написанном в разговорной форме и касающемся свойств прямоугольного треугольника с длиной сторон 3, 4, 5, имеется задача: "Доказать, что удвоенная сумма квадратов катетов треугольника без

Сократив обе части равенства на

R ²

, 4

получим 10 - 24- = 6 - 24- + 4 = 10 - 24- .

Средневековая Западная Европа унаследовала сведения из геометрической алгебры древних греков. Так, Абрахам Савасорда (Abraham Judaeus) из Барселоны (начало XIIв.) применил их при решении алгебраических уравнений и их систем. Его работы легли в основу "Practica Geometriae" (1224) Леонардо Пизанского. Для последнего случая он рас- x + У = 14, смотрел систему уравнений:            Са- xy = 48.

квадрата их разности равна квадрату их суммы". Тождество 2( a ² + b ²) – ( a – b )² = ( a + b )² китайцы доказывали геометрически (рис. 22): составляли квадрат ABCD

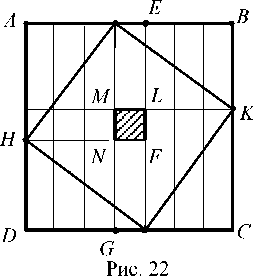
из 49 клеток. Тогда S _AEFH + S _KCGM + S _HNGD +

S _BKLE – S _MNFL = S _ABCD или 2S _AEFH + 2S _HNGD –

– S MNFL = S ABCD . В рассматриваемом случае 2(4² + 3²) – (4 – 3)² = (4 + 3)².

Аналогичная задача содержится в коммента-

васорда строил прямоугольник ABCD , площадь которого 48, и продолжил CD за точку С, так чтобы DC + CF = 14 (рис. 21). На от-

риях Конфуция к классическому труду "И – Кинг". В комментариях к трактату о "Чжоу-би" Чжан Цюнь Цинь (II–III вв.) привел следующую задачу, связанную с тео-

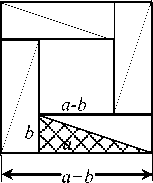
Рис. 23

ремой Пифагора: квадрат,

построенный на сумме длин катетов а и b треугольника ( а > b ), разбивал ее на восемь треугольников, равных исходному, и внутренний квадрат со стороной, равной разности длин катетов (рис. 23) [6].

Ученые стран ислама также проявляли интерес к геометрическим построениям. Автором трактата по алгебре "Краткая книга об исчислении алгебры и алмукабалы" является Мухаммед ибн Муса ал-Маджуси ал-Хорезми (787 - ок. 850). Она состоит из трех частей: алгебраической, геометрической и обширной книги о завещаниях. Целью автора было написание руководства по решению общежитейских задач. Он представил шесть канонических видов линейных и квадратных уравнений, которые записал без символики. Ал-Хорезми сформулировал лишь правила, дающие возможность получить положительные корни уравнений, и применил их при решении уравнений с числовыми коэффициентами.

Левая часть дополнялась до полного квадрата: x ² + 2-5 x + 25 = р9 + 25; ( x + 5)² = 8², откуда x + 5 = 8 и х = 3. Отрицательные корни не учитывались [7].

В "Трактате о геометрических построениях" Абу-л-Вафы ал-Бузджани (940-998) имеется задача: построить квадрат из двух квадратов, длина сторон которых неизвестна [8]. Он предложил наложить один из них ( ABCD ) на другой ( AEFG ) и продолжить смежные стороны ( BC и DC ) первого до пересечения в точках N и M соответственно со сторонами большего квадрата; N и M соединил с А (рис. 26, а ). Затем рассмотрел два равных прямоугольника AEMD , ABNG и маленький квадрат СMFN . Прямоугольники AEMD , ABNG разбивал диагоналями AM и AN на равные треугольники. Их катеты равны сторонам данных квадратов; CN - сторона CMFN - равна разности длин катетов этих треугольников. Автор расположил около ма-

После решения он приводил геометрические ленького квадрата четыре прямоугольных доказательства. Так, справедливость одного из решений уравнения x2 + 10x = 39, которое

треугольника с катетами, равными сторонам исходных квадратов (рис. 26, б ). Полученный

впоследствии было помещено во многие

квадрат HRTS равновелик сумме двух данных

арабские и европейские средневековые книги

квадратов с неизвестными длинами их кате-

по алгебре, доказывалось с помощью геометрических построений (рис. 24). Строится искомый квадрат x ², а на его сторонах - четы-

	2 x	5 x 2
		25

Рис. 24

ре прямоугольника

шириной

5/ / 2

В вер-

шинах квадрата до-

бавляются четыре квадрата с длиной стороны 5/Z . Полу-

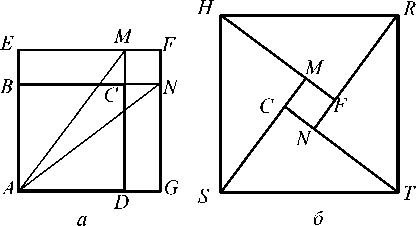
Рис. 26

ченный     большой квадрат имеет пло-

щадь

39 + 4 . (^ ) 2 = 64

и сторону x + 2 • 5/ = 8, поэтому х = 3.

Другое

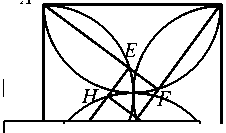
5 х       x²

тов [2] .

Еще в одной задаче предлагалось разделить данный квадрат на два квадрата, если длина стороны одного известна. Абу-л-Вафа на сторонах квадрата ABCD как на диаметрах B описал внутри его полуокружности (рис.

27). Затем он рассмотрел хорды AE = BF = CG = DH,   равные данной роне. Очевидно, отрезки AF = = BG = CH =DE образуют маленький

ческое доказательство решения этого ния приведено на рис.25.

5 х

квадрат EFGH и четыре равных прямоугольных треугольника AED, AFB, BGC, CHD . Исходя из решения предыдущей задачи, Абу-л-Вафа составил из этих треугольников и HEFG искомый квадрат [8].

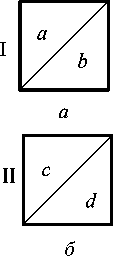
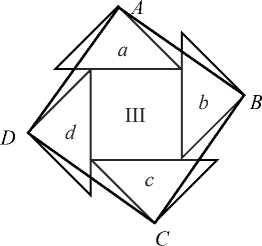
Из геометрических задач Абу-л-Вафы представляет интерес задача своеобразного построения квадрата, равновеликого трем равным квадратам. Ее решение было помещено во многих последующих руководствах (рис. 28, а-в ). Ученый разделил диагоналями пополам первые два квадрата (рис. 28, а , б) , полученные равнобедренные прямоугольные

Тогда остаток равен корню

[ x =

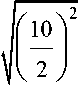
+ 39 - 5]" [7].

квадрата

Геометрическая интерпретация решения уравнения представлена на рис. 29. Пусть S _A bcd = x ². Увеличенный на десять корней [10 x ], он равен 39.

в

Рис. 28

F

E

K

A

B

10 x

Рис. 29

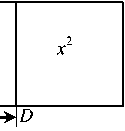
C

треугольники a , b , c , d приложил гипотенузами к сторонам третьего квадрата, так чтобы каждая вершина последнего совпадала с вершиной не более одного треугольника. Если вершины этих треугольников последовательно соединить отрезками AB , BC , CD и DA , то получится искомый квадрат. Абу-л-Вафа указал на неточность методов, которыми решали эту задачу ремесленники. Он использовал и другие методы, в частности, строил сторону утроенного квадрата, взяв в качестве исходной диагональ куба, построенного на одном из данных квадратов. Относительно последнего важным представляется замечание: "Точно так же обстоит дело, если мы хотим построить квадрат, состоящий более чем из трех или менее чем из трех квадратов" [8, С. 118].

Заметим, что большая часть книги, как выяснилось в 60-х гг. прошлого века, текстуально совпадает с написанной на полвека раньше "Книгой духовных искусных приемов и природных тайн о тонкостях геометрических фигур" Абу Насра ал-Фараби ( « 870-950) [2].

Арабские ученые использовали геометрическую алгебру и при решении уравнений. В трактате Омара Хайяма (XI в.) "Об алгебраических доказательствах" приведена задача, в которой содержатся словесные правила для геометрического построения уравнений. Она имела вид: "Квадрат и десять корней равны 39". Ученый привел следующее решение: "Умножь половину корней саму на себя. Это произведение прибавь к числу [39]; а из корня квадратного вычти половину числа корней.

Эти корни Омар Хайям представил в виде прямоугольника ADEF ; DE = AF =10. Точкой К разделил AF пополам. Произведение FB и BC , равное S _BCEF , сложенное с квадратом, построенном на АК , равно квадрату, построенному на ВК [(10 + x ) x + 25 = ( x + 5)²]. Но площадь квадрата на АК равна 25, а S _BCEF = 39. Следовательно, площадь квадрата на ВК и длина отрезка ВК известны [ x + 5]. После вычитания из ВК длины отрезка АК можно найти AD , т.е. искомый отрезок х [7].

Наиболее ранние геометрические знания индийцев представлены в "Шульба-сутре" (VI-V вв. до н.э.) - руководстве по возведе-

нию алтарей и храмов. Строения ориентировали по странам света, в основании же их лежали определенные фигуры, которые были подобными или рав-

новеликими геометрическими фи-

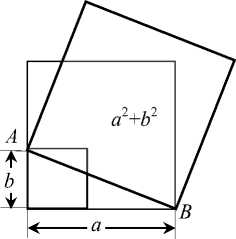
Рис. 30

гурами. Это требовало построения прямого

угла, квадрата, прямоугольных треугольников с целочисленными длинами сторон, построения из них трапеций, преобразования прямоугольника в равновеликий ему квадрат, преобразования квадрата, равновеликого сумме (рис. 30) или разности двух данных квадратов [9].

В процессе таких построений формулировались положения, которые впоследст-

вии появятся в трактатах древних греков: параллелограммы, построенные на одном основании и между одними и теми же параллельными линиями, равновелики (рис. 31).

B 2       C 2 B       C B 1       C i b

a

А         D

Рис. 31

Преобразование квадрата в равновеликий ему прямоугольник представлено на рис. 32 [9].

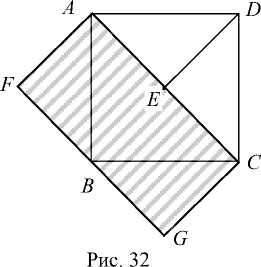
Построение:

• 1.    АС ;

• 2.    Е : Е е АС, АЕ = ЕС ;

• 3.    ED ;

• 4.    ^ AFB = ^ BGC = ^ AED . S acgf = S abcd.

Для построения квадратов, имеющих площадь в k раз больше площади данного, строили последовательно на диагоналях исходного квадраты со сторонами a42, a42, 2 а , a45 и т.д. Процедура построения квадратов с использованием теоремы Пифагора при k = 2 - 5 представлена на рис. 33.

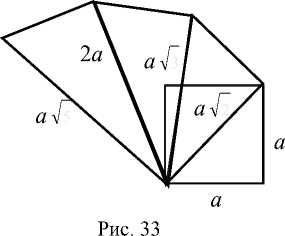
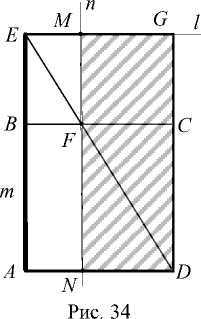
Для преобразования квадрата в прямоугольник, одна из сторон которого известна ( m ), выполнялись построения (рис. 34):

• 1.    [ AB );

• 2.    [ AE ]: E е [ AB );

• 3.    [ BC ], [ ED ];

• 4.    l : E е l, 1 1| [ BC ];

• 5.    F = [ BC ] n [ ED ], G = l n [ DC);

• 6.    n : F е n, n || [ AE ];

• 7.    M = l n n, N = n n [ AD ]. S nmgd = S abcd .

  
  
  

Во всех геометрических построениях в "Шуль-ба-сутре" важное место занимала теорема Пифагора. Составители руководства использовали шесть прямоугольных треугольников с целочисленными сторонами: 3, 4, 5; 5, 12, 13; 8, 15, 17; 7, 24, 25; 12, 35, 37 и 15, 36, 39.

Из этих и подобных им треугольников составлялись равнобедренные трапеции [9].

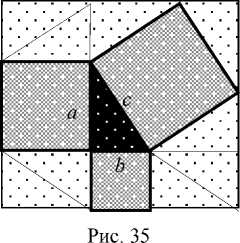
Среди геометрического материала ин- дусов имеется задача, также связанная с теоремой Пифагора: дан треугольник с катетами a, b и гипотенузой с. На каждой из его сторон построили квадраты. Следовало сравнить площадь квадрата, построенного на гипотенузе, с суммой площадей квадратов, построенных на катетах (рис. 35).

Ин-ские уче-проявляли рес и к решению ал-гебраиче-уравне-давая им метриче-интерпре-цию. Осо-

дий-ные инте реал- ских ний, гео-скую та-бый

интерес представляли неопределенные уравнения. Так, уравнение, содержащее произведение неизвестных: ах + by + c = xy , индийцы преобразовали в вид ab + c = xy - ах - by + ab ; ab + c = x ( y - a ) - b ( y - a ), тогда ab + c = = ( x - b ) - ( y - a ) (*). Если ab + c могло быть представимо в виде двух множителей, т.е. mn , то множество решений имеет вид x = m + b ;

y = n +a .

Алгебраическое преобразование доказывалось геометрически (рис. 36). Разность меж- ду площадью прямоугольника xy и площадью гномона (зашрихованная часть), равной ах + by – аb, представлялась, с одной стороны, площадью прямоугольника (x – b)(y – а), а с другой – площадью аb + c (по условию), откуда следует соотношение (*) [10].

Заключение

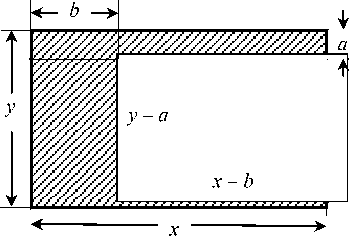
Рис. 36

Представленный материал позволяет раскрыть интерес ученых различных стран к геометрической алгебре. Заслуживает внимание также дальнейшее изучение форм передачи математических сведений древних греков ученым средних веков.