Влияние гибридизации эффективного парного потенциала на расчетные свойства жидкого железа

Одним из простейших вариантов модельного потенциала, применяемого при молекулярнодинамическом моделировании (МД), является эффективный парный потенциал (ЭПП). Среди методов получения ЭПП особенно выделяются методы расчета по известной структуре вещества. Часть наиболее известных методов, реализующих данный подход, описана в работе [1]. Среди них можно выделить метод Шоммерса [2, 3], являющийся исторически первой итерационной схемой, позволяющей рассчитать ЭПП, воспроизводящий экспериментальную парную корреляционную функцию (ПКФ) при моделировании методом МД. Причиной особого положения методов воспроизведения потенциала по структуре является взаимно однозначная связь между ЭПП и ПКФ. Единственность ЭПП, воспроизводящего заданную ПКФ, при условии его существования была доказана Хендерсоном [4], а существование такого потенциала доказано Чайесом с соавторами [5].

Несмотря на этот факт, численное воспроизведение ЭПП по данным структурного эксперимента любыми методами, аналогичными схеме Шоммерса, не является однозначным [6]. Однако это не противоречит теоремам Хендерсона и Чайеса, поскольку на самом деле отличающиеся потенциалы приводят к модельным ПКФ, различие между которыми очень незначительно. В то же время ЭПП при этом могут отличаться очень существенно и, как следствие, приводят к различающимся значениям термодинамических параметров системы. Возможность получения такого ряда ЭПП, воспроизводящих с определенной точностью одну и ту же ПКФ, была продемонстрирована и объяснена Д.К. Белащенко [6]. Сама процедура получения такого ряда функций была названа им гибридизацией ЭПП.

Понимание причины возникновения такого вырождения дает возможность учесть этот эффект при построении ЭПП. Например, в работе [7] авторы использовали этот принцип для получения ЭПП, воспроизводящего одновременно с ПКФ кривую фононного спектра. В [8] мы предложили алгоритм для получения ЭПП, воспроизводящего ПКФ в NPT-ансамбле (канонический ансамбль, при котором рассматривается система, состоящая из фиксированного числа частиц, при заданном давлении и температуре), при этом получаемый потенциал дает правильное значение плотности системы. Кроме этого, наш алгоритм приводит к ЭПП, содержащему свободный параметр, который не меняет ПКФ и плотность модели, но при этом существенно влияет на все остальные расчетные свойства.

К сожалению, оказалось, что, изменяя этот параметр, не всегда удается согласовать с экспериментом такие характеристики как коэффициент самодиффузии и динамическую вязкость вещества. При этом анализ локальной структуры показал наличие существенной зависимости структуры ближнего порядка от свободного параметра ЭПП.

В настоящей работе показано влияние гибридизации ЭПП на все основные термодинамические и структурные характеристики жидкого состояния вещества на примере жидкого железа при температуре 1923 К. На основании полученных результатов предложен критерий выбора наиболее оптимального ЭПП, воспроизводящего методом МД экспериментальную кривую ПКФ для заданного значения температуры и давления.

Алгоритм

Метод гибридизации ЭПП Д.К. Белащенко [6] состоит в следующем. Допустим, мы получили каким-либо из существующих методов [1] ЭПП фт (r), воспроизводящий необходимую ПКФ в NVT-ансамбле (канонический ансамбль, в котором фиксируется количество частиц, объем и температура системы) при необходимой температуре. Кроме этого, мы можем подобрать потенциал ф0 (r), который соответствует статическому равновесию этой же системы с такой же ПКФ. Такой потенциал можно подобрать, например, методом сопоставления координационного числа в модели и значения полученного из эксперимента [7]. В итоге оказывается, что потенциал ф(r) = фт (r) + Хф0 (r) тоже с хорошей точностью воспроизводит заданную ПКФ при некоторых значениях X в NVT-ансамбле. Это происходит, потому что равнодействующая сила на отдель- ном атоме при этом не меняется.

Ранее мы предложили алгоритм [8] на основе этого принципа, который позволяет подобрать ЭПП, воспроизводящий ПКФ в NPT-ансамбле, благодаря чему одновременно достигается согласие по плотности системы. При этом остается еще один подгоночный параметр ЭПП, который не искажает ни ПКФ, ни плотность системы, но при этом сильно влияет на другие термодинамические характеристики системы. В нашем алгоритме вместо того, чтобы подбирать потенциал ф ₀ ( r ) для статического равновесия системы мы пользуемся неоднозначностью метода Шоммер-са. При различных стартовых потенциалах метод Шоммерса приводит к различным итоговым потенциалам, которые почти с одинаковой точностью воспроизводят одну и ту же ПКФ в NVT-ансамбле. На данный момент мы можем получать три различных ЭПП, соответствующих одной и той же ПКФ. Для этого мы используем потенциал Леннард-Джонса с различными параметрами ( r min ; E min ) :

Фи ⁽ r ) = - E min [ ( r min / r ) ¹² - ² ( r min / r ) 6 ] •

Таким способом не удается получить больше трех различных решений методом Шоммерса. Изменение отталкивающей и притягивающей степеней не влияет на конечный результат.

Схема Шоммерса в силовом варианте [9] выглядит следующим образом:

F 1 (r ) = kigr) ,                                  (2)

g ( r )

f„ ,< r ) = f ( r ) + kT ^g '⁽ r ) g( ^r ) ^{- g (} r ) g '⁽ r ) , i + 1 v / IV/                   / \   / \          ⁷

g ( r ) g_i ( r )

где F_i ( r ) – эффективная силовая функция на i -й итерации; g ( r ) – целевая ПКФ; k – постоянная

Больцмана; T – температура; gi(r) – ПКФ на i -й итерации, получаемая из модели, построенной методом МД; функции со штрихом – производные соответствующих функций. ЭПП рассчитывается интегрированием силовой функции при условии, что потенциал на радиусе обрыва равен нулю. В качестве критерия качества получаемой ПКФ на каждой итерации рассчитывается не- вязка между целевой и модельной ПКФ:

1/2

d i =

1 N

- X ⁽ g ⁽ r j ) ^- g i ⁽ r j ⁾⁾²

N j=0                  _ где g(r) – целевая ПКФ, gi (r) – расчетная ПКФ на i -й итерации, N – количество точек в гистограммах целевой и модельной ПКФ. При расчете ЭПП методом Шоммерса также использовалась стандартная схема демпфирования. В этом случае новое приближение выбиралось по формуле

F i + 1 w ( r ) = pF i + 1 ( r ) + (1 - p ) F i ( r ), (5)

где F_i ( r ) – эффективная силовая функция на i -й итерации; p – коэффициент демпфирования, принимающий значения в интервале [0, 1].

После получения методом Шоммерса трех различных ЭПП ϕ ₁( r ) , ϕ ₂( r ) , ϕ ₃( r ) , воспроизводящих одну и ту же ПКФ в NVT-ансамбле, мы можем применить метод гибридизации следующим образом:

ϕhyb(r)=λ1ϕ1(r)+λ2ϕ2(r)+λ3ϕ3(r)(6)

при условии

λ1 +λ2 +λ3 =1.(7)

В силу условия (7) мы имеем только два свободных параметра гибридного потенциала (6). Перепишем уравнение (6) с учетом (7):

ϕhyb(r)=ϕ1(r)+λ21ϕɶ21(r)+λ31ϕɶ31(r).(8)

Здесь ϕ ɶ ₂₁( r ) = ϕ ₂( r ) - ϕ ₁( r ) , ϕ ɶ ₃₁( r ) = ϕ ₃( r ) - ϕ ₁( r ) . Построим два различных гибридных потенциала, воспроизводящих ПКФ в NPT-ансамбле с необходимой плотностью:

ϕ1NPT(r)=ϕ1(r)+λ21ϕɶ21(r)+λ31ϕɶ31(r) ,(9)

ϕ2NPT(r)=ϕ1(r)+λ2′1ϕɶ21(r)+λ3′1ϕɶ31(r) ,(10)

где ( λ ₂₁; λ ₃₁) и ( λ ₂ ′ ₁; λ ₃ ′ ₁) – два различных набора параметров гибридного потенциала (8). Теперь можно выполнить повторную гибридизацию: NPT NPT NPT

ϕhNyPbT(r) =ϕ1NPT(r)+λϕNPT(r) .(11)

Здесь ϕ ɶ ^NPT( r ) = ϕ ₂ ^NPT - ϕ ₁ ^NPT = ( λ ₂ ′ ₁ - λ ₂₁) ϕ ɶ ₂₁ + ( λ ₃ ′ ₁ - λ ₃₁) ϕ ɶ ₃₁( r ) . Изменение параметра λ (11) в некотором интервале значений практически не будет влиять ни на ПКФ, ни на плотность системы при расчете в NPT-ансамбле, но при этом будет существенно влиять на другие расчетные характеристики системы.

Расчет потенциала для жидкого железа при температуре 1923 К

В качестве целевой ПКФ использовали экспериментальные данные для жидкого железа при температуре 1923 К [10].

г, А

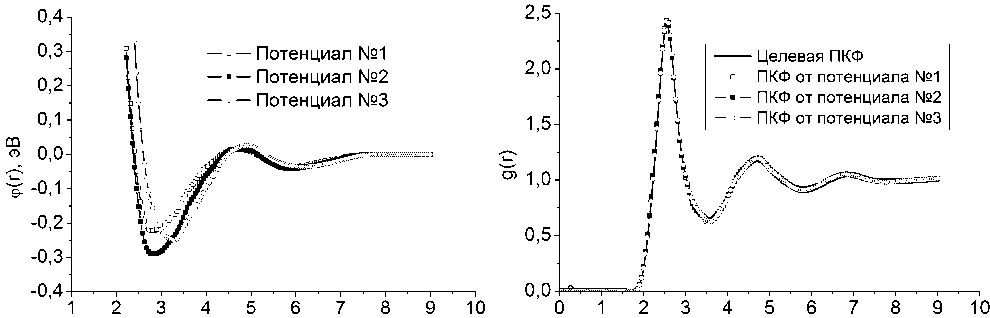
Рис. 1. Эффективные парные потенциалы, полученные методом Шоммерса с использованием различных стартовых потенциалов в форме Леннард-Джонса г, А

Рис. 2. Парные корреляционные функции, рассчитанные в NVT-ансамбле с различными эффективными потенциалами (рис. 1), в сравнении с экспериментальной кривой из работы [10]

Согласно описанному алгоритму, на первом этапе рассчитывались три различных ЭПП методом Шоммерса. Для этого были подготовлены три различных потенциала Леннард-Джонса (1) с различными параметрами (rmin; Emin) : (2, 5Å; -0,145эВ) , (2, 5Å; -0, 245эВ) , (2, 8Å; -0,145эВ) . С каждым из этих потенциалов был выполнен расчет ЭПП методом Шоммерса с коэффициентом демпфирования p = 0,5 . В итоге были получены три различных ЭПП (рис. 1), хорошо воспроиз- водящие целевую ПКФ в NVT-ансамбле (рис. 2). Невязки по ПКФ d для потенциалов № 1, № 2 и № 3 на рис. 1 составили: d1 = 0, 0329 , d2 = 0, 0326 , d3 = 0, 0298 соответственно.

Все расчеты методом МД в настоящей работе выполнялись при помощи пакета LAMMPS [11]. Расчет ПКФ при построении потенциала методом Шоммерса производился в NVT-ансамбле с использованием термостата Нозе–Гувера [12]. Система во всех случаях представляла собой куб с периодическими граничными условиями, состоящий из 1000 атомов. Объем модельного куба выбирали таким образом, чтобы атомная плотность была равна экспериментальному значению 0,0742 Å–3 [10]. Длина шага по времени была равна 1 фс. Расчет ПКФ выполнялся в два этапа. Сначала производили релаксацию системы с новым потенциалом в течение 5000 шагов. После этого полученную модель использовали в качестве стартовой конфигурации для дальнейшего МД расчета, в ходе которого рассчитывали модельную ПКФ. При этом моделирование выполняли в течение 1000 шагов, на каждом из которых рассчитывалась ПКФ. Итоговую кривую получали усреднением по всем 1000 шагам. Радиус обрыва потенциала и ПКФ во всех расчетах был равен 9,0 Å.

На следующем этапе рассчитывали два гибридных потенциала (9) и (10), подбирая соответствующие коэффициенты таким образом, чтобы получаемые потенциалы воспроизводили в NPT-ансамбле экспериментальное значение атомной плотности. В первом случае были получены значения ( λ ₂₁; λ ₃₁) = (0, 0; - 0, 43) , во втором – ( λ ₂ ′ ₁; λ ₃ ′ ₁) = (4, 0; 0, 65) . После этого семейство гибридных потенциалов, воспроизводящих ПКФ в NPT-ансамбле, определяется согласно выражению (11).

Методика моделирования

Для анализа влияния гибридизации ЭПП на свойства модели рассчитали кривые ПКФ и невязки d между целевой и модельными ПКФ, коэффициент самодиффузии D , коэффициент динамической вязкости η , коэффициент теплового объемного расширения β , атомную плотность n , потенциальную энергию системы U _pot . Все перечисленные характеристики рассчитывались в зависимости от параметра λ (11). Для более детального анализа структуры выполнили расчет основных структурных параметров методом многогранников Вороного. В качестве таких характеристик рассмотрели распределения по коэффициенту сферичности многогранников Вороного k_sph , по количеству граней у многогранников N_s , по объему многогранников V_VP и распределение G ( r ) .

Все перечисленные характеристики вычислялись по данным, полученным в результате моделирования в NPT-ансамбле при нулевом давлении. Все параметры модельного бокса использовали такие же, как при построении ЭПП методом Шоммерса. Во всех случаях систему предварительно выдерживали в течение 30 000 шагов с длиной шага 1 фс для достижения термодинамического равновесия. После этого выполняли 10 расчетов по 1000 шагов каждый с таким же временным шагом для набора статистики по необходимым для дальнейших вычислений параметрам. Для вычисления коэффициента β выполняли 30 расчетов по 1000 шагов для набора статистики.

Расчет ПКФ в NPT-ансамбле идентичен описанной выше процедуре расчета в NVT-ансамбле. Здесь также использовался термостат и баростат Нозе–Гувера [12, 13]. Отличие состоит только в использовании NPT-ансамбля вместо NVT-ансамбля, причем давление в баростате задавалось равным нулю. Невязку с целевой ПКФ рассчитывали согласно выражению (4).

Коэффициент самодиффузии вычисляли через угловой коэффициент прямой среднеквадратичного отклонения атомов от времени. При этом из расчета исключали значения при малых t , когда атомы движутся в баллистическом режиме.

Коэффициент динамической вязкости η рассчитывали методом Мюллера–Платца [14]. Идея метода состоит в том, что в процессе моделирования методом МД в системе искусственно индуцируется градиент скорости, характеризующий движение слоев жидкости. Средний слой движется с положительной скоростью относительно выбранной оси, а крайние слои движутся в обратном направлении. Для этого с определенной частотой выбирается одна или более пар атомов. В среднем слое выбираются атомы с самой низкой скоростью, а в одном из крайних слоев – атомы с самой высокой скоростью, после чего они обмениваются импульсами, в результате средний слой приобретает положительное направление скорости, а крайние слои – отрицательное. В на- Серия «Математика. Механика. Физика», выпуск 7 123

стоящей работе обмен импульсами выполнялся для одной пары атомов на каждом десятом шаге МД. Количество слоев, на которые условно разделялась модель, было равно десяти. Перед расчетом п равновесная по объему и энергии система дополнительно выдерживалась в течение 1000 шагов для получения равновесного градиента скорости. В результате во всех случаях был получен линейный профиль скорости ux относительно оси z. Далее расчет динамической вязкости п производили по известному выражению:

ди jp п a, оz

где j_p – поток импульса от среднего слоя к крайнему.

Коэффициент теплового объемного расширения в вычисляли по приблизительному соот- ношению:

2   V H V)

V V2) + V T2 - T , где V1 – средний объем модели после 1000 шагов МД при температуре T1 , и аналогично для параметров с индексом 2. Во всех случаях расчет производили при нагревании системы от 1723 К до 2123 К.

Атомную плотность n рассчитывали как отношение количества атомов модели к среднему объему системы. Усреднение объема производили по 1000 шагам МД.

Потенциальную энергию системы U pot вычисляли как сумму потенциальных энергий всех атомов.

Все характеристики структуры ближнего порядка были получены с использованием программы статистико-геометрического анализа структуры методом многогранников Вороного [15]. Большинство рассматриваемых в настоящей работе характеристик разбиения Вороного не нуждаются в пояснении за исключением k_sph и G ( r ) . Коэффициент сферичности k_sph определяет близость формы многогранника к идеальной сфере:

, - 36nV^г МАА k sph = J 5 ’ О⁴)

где V - объем многогранника, 5 - площадь его боковой поверхности. Для сферы k_sp h = 1. Распределение G ( r ) является аналогом ПКФ, но описывает относительное расположение ближайших соседей данного атома, определяемых только многогранником Вороного.

Анализ влияния гибридизации ЭПП на характеристики модели жидкого железа

Необходимо заранее отметить, что параметр X (11) можно изменять только в пределах некоторого интервала. Как будет показано ниже, при слишком низком или высоком значении X плотность системы и модельная ПКФ начинают сильно искажаться. В настоящей работе для анализа выбран интервал значений X [ - 0,3; 2,0 ] . В качестве примера на рис. 3 приведены графики ЭПП из ряда (11) для значений X = - 0,3, X = 0,0, X = 1,0, X = 2,0.

В таблице приведены расчетные значения всех термодинамических характеристик модели, описанных в предыдущем разделе. Все физические свойства модели рассчитаны для различных значений параметра X (11).

На рис. 4 приведены ПКФ, рассчитанные в NPT-ансамбле с нулевым давлением в баростате с использованием потенциалов, показанных на рис. 3. Как видно из рис. 4, ПКФ при X = 2,0 уже существенно отличается от целевой кривой на всей области определения. В это же время все остальные кривые, включая результат при X = -0,3 - другом крайнем значении свободного параметра потенциала, остаются очень близки к искомой ПКФ. Для количественного сопоставления полученных кривых в таблице приведены невязки по ПКФ d для различных значений X. Среди всех этих значений можно выделить явный минимум при X = 1,0. При движении X в меньшую или большую стороны от этого значения невязка монотонно возрастает. Максимальное значение доверительного интервала невязки для вероятности 99 % составило Ad = 0,002, что гораздо ни- же, чем диапазон значений невязки в зависимости от λ. По этой причине можно рассматривать минимум по невязке как критерий выбора наиболее оптимального ЭПП из ряда (11). Кроме того, такой критерий согласуется с теоремами Хендерсона [4] и Чаейса [5], согласно которым сущест-

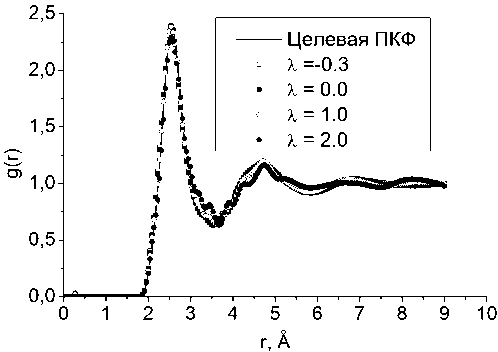
Рис. 4. Парные корреляционные функции, рассчитанные в NPT-ансамбле при нулевом давлении с различными гибридными потенциалами (рис. 3), в сравнении с экспериментальной кривой из работы [10]

вует только один ЭПП для данной ПКФ.

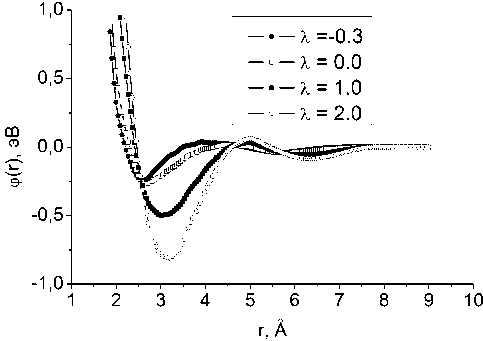
Рис. 3. Гибридный эффективный парный потенциал для различных λ , воспроизводящий ПКФ в NPT-ансамбле при нулевом давлении

Расчетные свойства жидкого железа при температуре 1923 К с различными парными потенциалами

	d , 10–2	–3 n ,	U pot , кДж/моль	β , 10–5 К–1	D , 10–5 см2/с	η , мПа·с
Эксперимент	–	0,0742 [10]	–	16,7 [16]	3,61 [17]	5,04 [16]
λ =- 0,3	0,041	0,0724	–123,5	11,9	8,3	1,9
λ = - 0, 2	0,040	0,0732	–143,2	10,4	8,2	2,0
λ = - 0,1	0,039	0,0738	–162,9	9,2	7,6	2,0
λ = 0,0	0,038	0,0741	–182,2	8,6	7,8	2,1
λ = 0,1	0,038	0,0743	–201,4	8,2	7,7	2,1
λ = 0,3	0,036	0,0746	–239,9	7,5	7,4	2,0
λ = 0,5	0,034	0,0747	–278,4	7,3	7,6	2,1
λ = 1,0	0,032	0,0744	–374,6	6,4	7,6	2,1
λ = 1,5	0,036	0,0732	–471,1	5,7	7,8	2,3
λ = 2,0	0,055	0,0713	–568,3	3,7	7,6	2,3

Следующим наиболее важным параметром является плотность системы. Поскольку используемая экспериментальная ПКФ соответствует строго определенному значению атомной плотности n , то оптимизация гибридных потенциалов (9) и (10) изначально производится для согласования плотности модели и экспериментального значения. Тем не менее в пределах небольшой невязки d , различные гибридные потенциалы приводят к несколько отличающимся значениям плотности (см. третью колонку таблицы). Вообще говоря, не получив согласия по плотности, нельзя добиться хорошего согласия по ПКФ. Это подтверждается сравнением значений в колонках 2 и 3 таблицы. Видно, что наименьшее значение невязки соответствует наилучшему совпадению расчетной и экспериментальной плотности. Таким образом, можно предложить следующий метод получения оптимального ЭПП: варьируя λ в выражении (11), можно найти значение, при котором достигается минимальное значение невязки по ПКФ одновременно с наилучшим согласием по атомной плотности системы.

Потенциальная энергия системы U _pot зависит от λ линейно (см. таблицу). Линейную зависимость U _pot от λ очень легко объяснить. Зная ЭПП и ПКФ, потенциальную энергию можно рассчитать аналитически следующим образом:

∞

U_pot = 4 π n ∫ ϕ ( r ) g ( r ) r ² dr .

Подставляя вместо ϕ ( r ) потенциал (11), и, учитывая, что ПКФ при этом почти не зависит от λ , выражение (15) переписывается следующим образом:

U_pot = 4 n n J p N ^PT( r ) g ( r ) r ² dr + A 4 n n J p ^NPT( r ) g ( r ) r ² dr 0                           L 0

Отсюда видно, что второе слагаемое представляет собой угловой коэффициент прямой U _pot ( λ ) , а первое слагаемое – значение U_pot при λ = 0,0 .

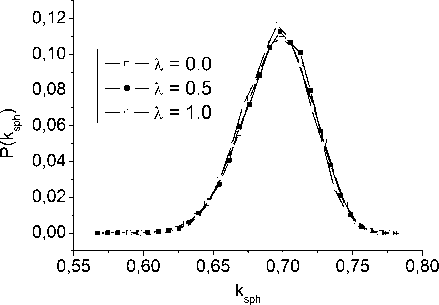
Рис. 5. Распределение многогранников Вороного по коэффициенту сферичности k _sph при различных значениях параметра λ

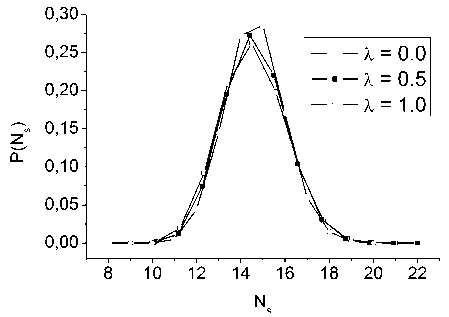
Рис. 6. Распределение многогранников Вороного по количеству граней при различных значениях параметра λ

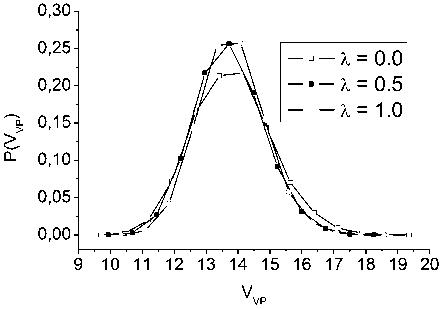
Рис. 7. Распределение многогранников Вороного по объему при различных значениях параметра λ

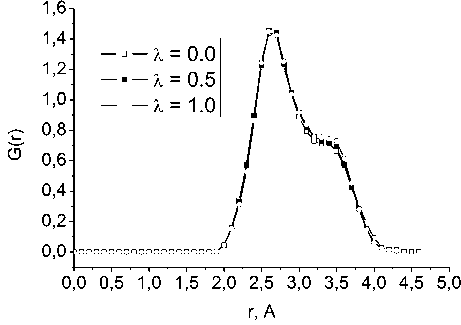
Рис. 8. Распределение G ( r ) при различных значениях параметра λ

Коэффициент объемного расширения β сильно зависит от параметра λ (см. таблицу). При уменьшении λ коэффициент β начинает быстро возрастать. Это связано с увеличением крутизны отталкивающей ветви ЭПП (см. рис. 3). На всем диапазоне λ нет согласия β с экспериментальным значением для жидкого железа при температуре 1923 К – различие составляет от 1,5 до 2 раз.

Точно так же обстоит дело и с воспризводимостью коэффициента самодиффузии D и динамической вязкости η жидкого железа. Семейство гибридных потенциалов (11) для температуры 1923 К дает заниженное приблизительно в два раза значение вязкости η по сравнению с экспериментом [16] и наоборот в два раза большее значение самодиффузии D по сравнению с данными первопринципного МД моделирования [17]. При этом параметр λ очень слабо влияет на значения η и D (см. таблицу). Здесь возможной причиной может быть следующее. Можно пока- зать, что ряд базовых потенциалов, формирующих сумму (6) не является полным, то есть существует еще множество линейно независимых потенциалов, которые воспроизводят данную ПКФ в NVT-ансамбле. Поэтому можно предположить, что полученный в настоящей работе ЭПП не является истинным, но его можно улучшить, если продолжить ряд базовых потенциалов в уравнении (6).

На рис. 5–8 показаны кривые распределений коэффициента сферичности k_sph , количества граней многогранников N_s , объема многогранников V_VP и G ( r ) соответственно. Распределение по коэффициенту сферичности k_sph и G ( r ) (рис. 5, 8) не завися от X в диапазоне [ 0,0;1,0 ] , в котором плотность модели меняется незначительно (см. таблицу). Но кривые распределений N_s и V VP (рис. 6, 7) оказались различными. Оба распределения с ростом X становятся существенно выше и сужаются. Это говорит о том, что структура ближнего порядка относительно этих характеристик становится более однородной. Но главный вывод здесь состоит в том, что гибридизация ЭПП может существенно влиять на структуру ближнего порядка получаемых моделей, в то время как ПКФ (рис. 4) при этом оказываются очень близки друг к другу.

Заключение

Предложенный в работе [8] алгоритм гибридизации ЭПП по принципу Д.К. Белащенко [6] был успешно применен для жидкого железа при температуре 1923 К. Метод позволяет получать целое семейство ЭПП, воспроизводящих ПКФ в NPT-ансамбле при МД моделировании. В свою очередь, воспроизведение ПКФ в NPT-ансамбле при заданном давлении приводит к автоматическому согласию по плотности модели с экспериментом. Несмотря на это, получаемый ряд ЭПП приводит к существенно различным значениям остальных термодинамических свойств модели жидкости. Анализ структуры ближнего порядка на примере жидкого железа тоже показал существенное влияние гибридизации ЭПП на такие характеристики локальной структуры, как распределения по объему и по количеству граней многогранников Вороного.

Существенным недостатком предложенного метода остается невозможность согласования с экспериментом основных транспортных свойств – коэффициента диффузии и динамической вязкости. Особенно учитывая, что вязкость является очень чувствительной к структурным изменениям характеристикой, а по результатам настоящей работы видно, что гибридизация ЭПП существенно влияет на структуру ближнего порядка, но при этом никак не сказывается на получаемых значениях диффузии и вязкости. Возможной причиной здесь можно назвать неполный ряд базовых потенциалов, используемых при построении гибридного ЭПП. Поэтому темой следующей работы будет поиск таких базовых функций для расширения этого ряда.