Влияние характера стружкообразования на распределение контактных нагрузок на фаске износа резца

Для расчета износостойких покрытий и оценки прочности инструмента необходимо знать величину и характер распределения контактных нагрузок на поверхности инструмента. При резании труднообрабатываемых материалов, таких как титановые и жаропрочные сплавы, эта задача особенно актуальна вследствие интенсивного износа инструмента. В этих случаях инструмент изнашивается в основном по задней поверхности, что вызывает увеличение сил резания и повышение вероятности разрушения режущей части инструмента.

В ряде экспериментальных и теоретических работ [1-3] показано, что силы на задней поверхности режущего инструмента являются результатом по крайней мере двух процессов: 1) упругого восстановления материала заготовки, сжатого волной деформации, опережающей резец; 2) подмятия под заднюю поверхность части срезаемого слоя, обусловленного наличием фактического округления режущей кромки инструмента.

На рис. 1, а показана наиболее часто реализуемая схема свободного резания - свободное строгание образца в виде прямоугольной пластины, закрепленной по линии АБ . Упругое напряженное состояние, которое создается в такой пластине при резании, можно рассматривать как плоское, а малые размеры зоны резания по сравнению с размерами самой пластины позволяют использовать при анализе этого состояния известные решения плоской задачи для полу-бесконечной плоскости.

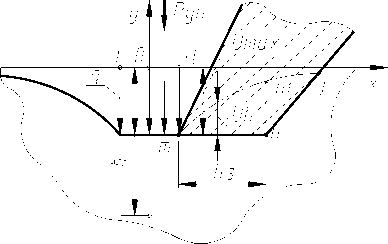
Рис. 1. Прогиб обработанной поверхности под действием силы Р _уп на передней поверхности: а - положение условной плоскости сдвига; б - положение обработанной поверхности

Характер взаимодействия с пластиной-полуплоскостью инструмента, имеющего пренебрежимо малый радиус округления режущей кромки, но конечную ширину h _з фаски на задней поверхности, показан на рис. 1, б .

Движение зоны стружкообразования перед резцом сопровождается распространением волны упругой деформации, что приводит к опусканию границы полуплоскости на величину U _max. При этом восстанавливающаяся позади режущей кромки поверхность mn 1 j взаимодействует с плоскостью фаски, дополнительно деформируясь до положения mnj .

В теории упругости подобная задача называется смешанной задачей для полуплоскости, на участке [- 1 , 1 ] границы которой заданы напряжения, а на участке [ 1 , 1 + h₃ ] заданы перемещения. Получение корректного решения данной задачи для реальных условий резания существенно затруднено, поэтому примем следующие допущения:

• 1.    Вследствие малости толщины среза а по сравнению с размерами пластины ступенчатостью верхнего края пластины можно пренебречь, считая, что на напряженно-деформированное состояние за режущей кромкой она влияет незначительно.

• 2.    Длина участка [ - 1 , + 1 ], нагруженного напряжениями, равна проекции условной плоскости сдвига на границу полуплоскости:

• 3.    На участке [ - 1 , + 1 ] действуют только нормальные напряжения, равномерно распределенные по его длине.

• 4.    Инструмент взаимодействует с поверхностью mnj как жесткое тело.

2 1 = a ctg Ф ( а - толщина среза; Ф - угол условной плоскости сдвига).

Переход от упругих деформаций фаской износа обработанной поверхности к контактным нагрузкам на задней поверхности затруднен. Поэтому использовалось решение задачи Буссинеска о воздействии силы на упругое полупространство, из которого было получено уравнение для кривой упругого восстановления

U ( x ) = - 1— ^-1 ² q ^f 0,14 + ^{113 1} ) ,                          (1)

Ex v x )

где q = P _/n/ ( b1 ).

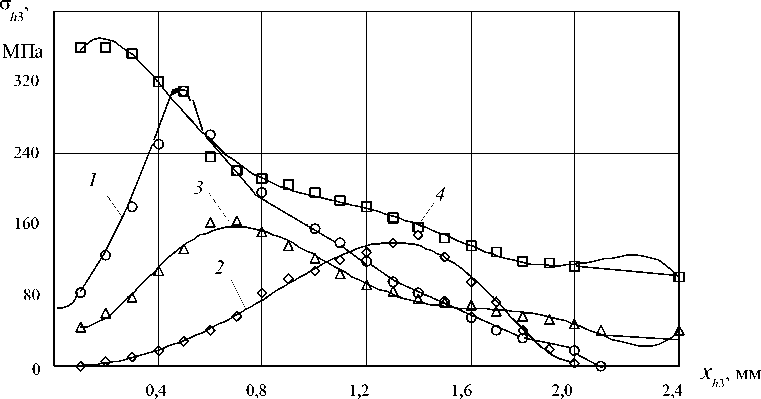
Рис. 2. Распределение нормальных контактных нагрузок на фаске задней поверхности инструмента (у=0°, а _ф = 0°, материал - Л63-Р6М5):

1 - S = 0,06 мм/об, V = 100 м/мин; 2 - S = 0,21 мм/об, V = 100 м/мин; 3 - S = 0,21 мм/об, V = 217 м/мин; 4 - ЛМцА 57-3-1 - Р6М5, S = 0,41 мм/об, V = 100 м/ мин

В экспериментах осуществлялось свободное точение ступенчатого диска с поперечной подачей. Достаточно большой радиус r _д диска и соответственно малая кривизна границы деформируемой области позволяют использовать полученные формулы. Для этого необходимо внести соответствующие коррективы реальной кривизны недеформированной границы полуплоскости. Силовое воздействие определяется величиной U_h :

U

h

1— ^V- lq [ 1,27

E I

0,14 1  1,13 1 ² )

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^.   ^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

x x ²     ,

- Гд +

[ r2 - (x -1 )2 ] °’5.

Зависимость (2) имеет максимум, координата х ₀ которого определяется параметрами P _уп, b , 1 , r _д, смещаясь вправо (удаляясь) от режущей кромки по мере повышения интенсивности силового воздействия на участке [- 1 , 1 ].

Аналогичный вид имеют эпюры нормальных контактных нагрузок:

C h з = 0,64 q 1,27

^^^^^^^в

0,14 1 1,13 1 ² )

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^.   ^^^^^^^^ ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

x x ² J

0,64 E (1 - v ²) I

^Г д

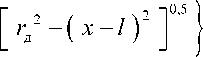
На рис. 2 приведены результаты экспериментального определения нормальных контактных нагрузок на фаске mn , выполненного методом разрезного резца при свободном точении латуни Л63 в условиях сливного стружкообразования. Экстремальный характер зависимости четко виден во всех случаях. По уравнению (3) было рассчитано распределение нормальных контактных нагрузок о _{h з} для тех же режимов резания (рис. 3). Необходимые исходные данные были взяты из эксперимента.

Сравнение расчетных и экспериментальных данных показывает, что координата х ₀ максимума эпюры зависит от режимов резания, как и величина контактных нагрузок. При этом наблюдается хорошая корреляция между расчетными и экспериментальными значениями ( S = 0,06 мм/об и S = 0,21 мм/об при V = 100 м/мин).

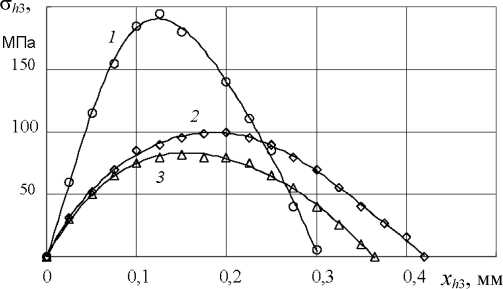
Рис. 3. Распределение нормальных контактных нагрузок на фаске задней поверхности инструмента при точении диска диаметром 200 мм, рассчитанные по формуле (3) (Л63-Р6М5, у=0°, а _ф = 0°): 1 - S =0,06 мм/об, V =100 м/мин; 2 - S =0,21 мм/об, V =100 м/мин; 3 - S =0,21 мм, V =217 м/мин

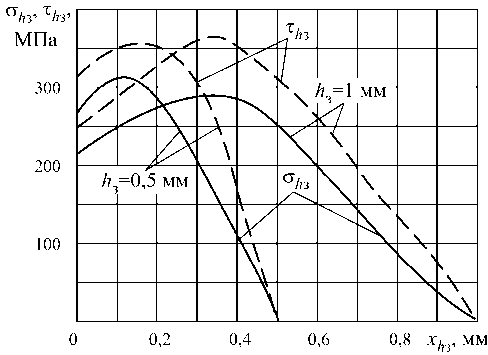
Рис. 4. Распределение контактных нагрузок на фаске задней поверхности резца при точении алюминиевого диска (у=10°, а _ф = 0°, V =0,6 м/мин, S =0,2 мм/об) [4]

Экстремальный характер эпюр нормальных о _{h з} и касательных т _{h з} контактных нагрузок был отмечен также в других работах [4] (рис. 4), однако объяснения этого явления отсутствуют.

Прогиб поверхности среза, рассмотренный выше, возникает под действием сил со стороны передней поверхности. При сливном стружкообразовании эти силы достаточно стабильны. При элементном стружкообразовании характер взаимодействия инструмента с поверхностью среза существенно изменяется. Последний этап формирования элемента стружки - отделение его от заготовки - сопровождается резким уменьшением (иногда до нуля) нагрузки в зоне стружкооб-разования на участке [- 1 , 1 ]. При этом упруго восстанавливающаяся поверхность среза создает дополнительное давление, приближенно пропорциональное перемещению U ( x ) и, следовательно, тем большее, чем ближе находится рассматриваемая точка к режущей кромке. Согласно уравнению (1) эта дополнительная пульсирующая нагрузка должна быть значительно больше по амплитуде, чем нагрузка, обусловленная деформацией поверхности среза при сливном стружкообразовании, определяемой величиной U ( h ). Наличие пульсирующей дополнительной нагрузки приводит к изменению закона распределения нормальной контактной нагрузки вдоль фаски mn : в этом случае наибольшее значение нагрузки должно наблюдаться вблизи режущей кромки.

Описанный механизм взаимодействия инструмента с поверхностью среза хорошо подтверждается рис. 2, на котором представлены результаты измерения нормальных контактных нагрузок на фаске mn при резании хрупкой латуни ЛМцА57-3-1 с элементным струж-кообразованием. Наибольшие нагрузки, как и предполагалось, наблюдаются вблизи режущей кромки.

При обработке титанового сплава ВТ3-1, сопровождающейся образованием элементной стружки, наибольшие нормальные контактные нагрузки также наблюдаются вблизи режущей кромки (рис. 5).

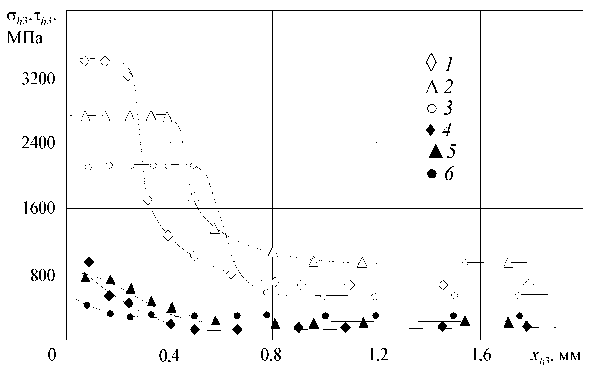
Рис. 5. Распределение нормальных ( 1 - 3 ) и касательных ( 4 - 6 ) контактных нагрузок на фаске задней поверхности инструмента при резании титанового сплава ВТ3-1 - ВК8 (у=0 ^о , а _ф = 0 ^о , V = 60 м/мин):

1 , 4 - S =0,41 мм/об; 2 , 5 - S =0,21 мм/об; 3 , 6 - S =0,11 мм/об

Выявленное влияние характера стружкообразования на распределение контактных нагрузок на фаске задней поверхности инструмента объясняет повышенный износ задней поверхности инструмента при обработке материалов, сопровождающиеся элементным стружкообразованием.

Проведенные исследования позволяют сделать следующие выводы. Характер распределения контактных нагрузок на фаске задней поверхности зависит от характера стружкообразования вследствие прогиба поверхности среза. При сливном стружкообразовании максимальное значение нормальных контактных нагрузок располагается на некотором расстоянии от режущей кромки инструмента, зависящем от интенсивности нагрузки в области стружкообразования.