Влияние характеристик базальтового расплава на процесс образования волокон

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 553.2+539.4                                    

Современная теория волокнообразования из расплавов горных пород, в том числе базальтового расплава, отражает в какой-то мере физический механизм этого сложного процесса и определяет пути совершенствования методов получения неорганических волокон.

В работах [1–3] достаточно подробно описан процесс образования волокна из расплава горных пород. В указанных работах рассматриваются различные схемы образования волокна. В одной из схем за основу берется предварительное расщепление расплавленной струи каким-либо энергоносителем на отдельные структуры (карли), из которых затем получают волокна посредством вытягивания. Предлагается также схема в виде прямого вытягивания волокон из горного расплава, которое происходит за счет трения, возникающего между энергоносителем и, непосредственно, расплавом.

Кроме того, в статье [4–6] рассмотрен процесс волокнообразования в присутствии акустического поля. Показано, что при построении теории волокнообразования в присутствии акустического поля желательно брать за основу капиллярно–волновую и кавитационную гипотезы.

В любом производстве изделий на основе минеральных волокон одним из основных видов оборудования, входящего в линию по производству изделий из волокна являются установки для формования базальтового ковра, или так называемые камеры волокноосаждения [7–9]. От их совершенства зависит качество готовых изделий. В настоящее время существует несколько широко используемых в промышленности способов получения минеральных волокон из расплава, которые и обуславливают различные типы и конструкции камер волокноосаждения. Во всех камерах формование минераловатного ковра происходит под действием гидродинамических сил. Поэтому изучение таких гидродинамических характеристик, как скорости падения отдельных волокон и сгустков из этих волокон и гидродинамическое сопротивление ковра, имеют первостепенное значение при проектировании новых и реконструкции старых камер волокноосаждения [1].

Целью настоящей работы является исследование взаимосвязи между скоростью деформации и коэффициентом вязкости базальтового расплава в процессе волокнообразования при посредстве дутьевой головки.

Материал и методы исследования

В исследованиях была использована дутьевая головка [10], представленная на Рисунке 1. Дутьевая головка состоит: из корпуса 1 с вводом 2, через который подается энергоноситель; верхнего покрытия 3 с отверстием 4 в центре и вводом 5, через который подается расплав; разъемного стакана 6 с фланцем 7, размещенного коаксиально корпусу 1; кольцевого сопла 8, образованного стаканом 6 и сопловым патрубком 5; генератора акустических колебаний 9, образованного кольцевой проточкой во фланце 7 стакана 6; досопловой 10 и подсопловой 11 камер, соединенных между собой посредством кольцевого сопла 8, тангенциальных каналов 12 и дополнительных прямоструйных сопел 13, которые выполнены во фланце 7 стакана 6.

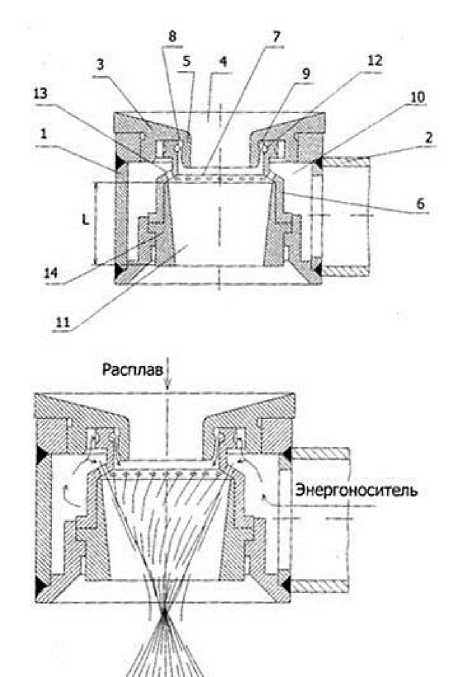
Рисунок 1. Дутьевая головка для получения супертонких волокон диаметром 0,5–2,5 мкм.

Такая конструкция дутьевой головки обеспечивают ее эффективную работу и получение супертонкого базальтового волокна диаметром 0,6–2,5 мкм и длиной 30–50 мм (Рисунок 2).

Для описания процесса расщепления волокна в дутьевой головке представим выходящий расплав в виде стержня из вязкого вещества (базальтового расплава), с бесконечно малыми сдвиговыми характеристиками в поперечном направлении и находящегося под действием растягивающих сил ± F, приложенных к его концам.

Рисунок 2. Расщепление базальтового расплава в волокно.

Согласно теории вязкого течения [11–12] распределение скоростей образующих течение частиц вокруг неподвижной нейтральной точки описывается следующими формулами:

ϑx = αx,

ϑy = - αy, ϑz = - αz,

где α(t) — параметр, характеризующий градиент скорости. Этот параметр зависит от времени. Если обозначить длину стержня (из базальтового расплава) через l (t), то для момента времени t, получаем, согласно формуле (1):

dl        l

dt = α 2,

где α⁄2 — коэффициент линейного растяжения базальтового расплава (стержня) за единицу времени.

Для определения зависимости коэффициента α от приложенной силы F заметим, что работа:

А = F∙dl = 1 Flα.                                             (3)

dt 2

Малые смещения частиц упругого тела под действием внешних сил можно охарактеризовать вектором смещения, который зависит от трех пространственных координат s(x, y, z).

Изменение положения частиц по отношению к выбранной точке можно описать с помощью градиента вектора смещения вдоль радиус-вектора:

ds dr

=1(ds+∇s)+1(ds-∇s)

2 dr         2 dr

Действием даже малых внешних воздействий, но, если их длительность велика, происходят изменения среды характерные при деформациях [13]. Т. е. при деформациях частицы среды приобретают определенную скорость. Описать смещения в структуре среды, при условии, что длительность внешнего воздействия очень мала, можно с помощью вектора перемещения, который пропорционален скорости частиц среды:

s(x,y,z) = B(x,y,z)At

Выражение для скорости через его пространственные компоненты имеет вид:

В =

Деформация жидкости определяется значениями производных скоростей вблизи данной точки, т. е. при изучении деформаций упругих тел важны не столько вектора перемещений, а значения скоростей частиц среды [14]. Изменение скоростей частиц среды вблизи рассматриваемой точки можно задать следующим соотношением:

d(r + dr) = i9(r) + ^r,                                      ⁽⁶⁾

Производная вектора скорости вдоль радиус-вектора, выраженная через пространственные компоненты, может быть представлена в виде следующей матрицы:

dB dr

/дВ дВ д^х
дх  ду dz
дВ2  дВ2 дВ2	( dB\T
	; та=Ы
дх  ду дz
дВ3 дВ3 дВ3
1                                                           1
\ дх  ду дz /

Если соотношение (6) рассматривать ка тензор, то его можно представить в виде суммы тензоров скоростей деформации и вращения:

dB dr

^e+^+i^-™)

2 dr         2 dr

Изменение скорости при удалении от рассматриваемой точки вдоль некоторого радиус-вектора, начало которого в этой точке, можно выразить через ротор поля векторов скоростей изучаемой среды:

B(r + dr) = B(r) + Bikdr + -rotB x dr.

Здесь B i _k — тензор скоростей среды, и он определяется соотношением:

1/d^

"*= ^UH

Или в матричном представлении:

Ък =

/

дт^ ду

1^+д^|

2 дх ду

1/^+д^

2 ду дх д^ ду

1^+д^\ 2 ( dz + дх )

1 д^3 д^2

2 \ dz ⁺ ду

1/^+д^ 1(д^+д^

д^ з dz

/

\2 ( дх + dz )  2 ( ду + дz )

Применение формулы (11) для описания работы (работа рассчитывается на единицу объема среды) сил внутреннего трения, обусловленных вязкостью среды, дает следующее соотношение:

A=2]lilk^k

^^ш

В случае рассмотрения движения, описываемого формулами (1), $ 11 = а, $₂₂ = $ 33 а/2, остальные компоненты тензора $ ik обращаются в нуль.

Полная работа сил трения во всем объеме стержня V = Sl (S-поперечное сечение в рассматриваемый момент) выражается следующей формулой:

.    3

A = -pVa2

Приравнивая ее к работе растягивающей силы  F(dl/dt), — получаем следующее соотношение для коэффициента α (градиента скорости течения),

3pVa2 = Fla, т. е.

а=^

3]V

Для описания процесса волокнообразования в дутьевой головке воспользуемся уравнением энергобаланса в следующем виде:

3     ,   d(o5)   1

- ]7a2 + —т— = -Fla

2          at    2

Здесь п — вязкость базальтового расплава; V — объем расплава; a — градиент скорости деформации; о — поверхностное натяжение базальтового расплава; S — площадь поверхности; F — вытягивающая сила; l — длина.

Первое слагаемое в уравнении (14) представляет собой работу сил внутреннего трения, второе слагаемое определяет скорость изменения поверхностной энергии, правая часть описывает работу внешних сил. При достаточно больших скоростях вытяжки волокон работа, затрачиваемая на преодоление вязкости, значительно превосходит работу затрачиваемую на преодоление сил поверхностного натяжения, т. е.:

- ]Va2 = 2 Fla

Преобразуем уравнение (15) к следующему виду | pVa = | Fl • 1 dl      F

Используя (2), получаем —— =    .

Принимая во внимание, что V = Sl и F = PS, получаем:

1a = —at l      6]

После интегрирования уравнения (16) получим:

l

Г^ ^(^) ⁰ 6n(t)

at].

Здесь l — длина волокон; P(t) — удельная сила, величина которой и зависимость ее от времени определяются конструкцией дутьевой головки, давлением подаваемого пара и другими факторами; l0 — характерный размер элементарного объема струи расплава в начальный момент времени; n(t) — вязкость расплава; t — время.

При условии, что плотность расплава в процессе охлаждения изменяется незначительно, из уравнения сохранения массы получаем:

V = V o

nd²l _ nd 2 l₀

.

Здесь V — объем волокна; V0 — объем струи базальтового волокна.

Отсюда диаметр поперечного сечения волокна можно выразить через его длину:

Площадь волокна или струи равна s = 2nr2 + 2nrl = 2n(r + l); r << l, s = 2nrl = ndl = 2VnVL

d(as) ^—^_ ^^

dt

a ds = a = „2^ » £ = _oJПV7i d^ . dt        dt               2Vl dt              dt

ads dt

dl dt

l^ya2 =^y

dV (dt)

I2

Сравнивая выражения (2) и (3), получаем формулу оценки:

a ds ^Va²

.------dl 2 a^'V/idt'l

l2

■<)

2 a 2  1

,--------  2   l2

7 = aVПV/i•|—dr = nVdt ds

2 a nVl2  1   _ _

3П  lVr-d[-l = “

N       dt

■

nl 1

V - dT4

dt

4 a 1 l

3 n d dl 1   3 n dl d

dt

dt

adt _ 4a 1 l lтlVa2   3ndld

2nVa      dt

На основании (14) и (18) имеем:

- nVa2 + o^nV/l • — = - Fla dl

a = -;—7 dt • l |-nVa2 + o7ПV7i•-^-2l                        dt • l

—nVa2 + a^nV/i •

= - Fa 2

a = - Fa

^nVa2 = 1Fa

-

2inVa=2F

•a ^nVa² = “(|f - a^nV/l)

1              ,-------

-

1F a = —

-

1F a^

-

o^nV/l iP-S

-

l

2lnV o^nV/l

2P‘V/l

-

2lnV

2lnV

2lnV

Я ©

_ 1P-VV/i •Vv/i-

^nv               |n •VV/i      3n 3n •VV/l

P   2aVn   P    2aVn    P    2a    P4a

3n 3n •Vs 3n 3n •Vnr2 3n 3n т 3n 3n •d 1      4a      14a\

3П(, Т)“

Технологические параметры и расчетные значения скорости деформации приведены в Таблице.

Таблица.

ТЕХНОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ РАСПЛАВОВ ИЗ БАЗАЛЬТОВЫХ ГОРНЫХ ПОРОД

Месторождение	Вязкость, ц Па • с, при t, °C
	1450	1400	1350	1300	1250
Сулуу–Терек (Кыргызстан)	4,7	8,4	14,0	24,5	47,0
Берестовецкое (Украина)	3,6	6,2	10,2	18,2	35,4
Марнеульское (Грузия)	7,8	13,0	22,5	41,0	76,5
Давление энергоносителя, P, кг/с			5
Диаметр волокна, d, мкм			0,5–2,5
Коэффициент поверхностного натяжения, среднее значение ст, н/м			0,2–0,5
Месторождение	Скорость деформации, с			1, при t,	°C
	1450	1400	1350	1300	1250
Сулуу–Терек (Кыргызстан)	4283,62	2396,79	1438,07	821,76	428,36
Берестовецкое (Украина)	5592,50	3247,26	1973,82	1106,21	568,73
Марнеульское (Грузия)	2581,15	1548,69	894,80	491,05	263,18

Из данных Таблицы видно, что с увеличением температуры расплава его вязкость увеличивается, также увеличивается скорость деформации. Поэтому слишком большое увеличение малых деформаций может стать основой появления отходов волокнообразования.

Экспериментально определена вязкость расплава в зависимости от химикоминералогического состава электродуговой печи для диапазона температур 1250–1450 °С [13–15]. В соответствии с полученными результатами изменение скорости деформации в процессе волокнообразования происходит в пределах 428,36–4283,62 с-1.

Таким образом, при выходе за пределы скоростей деформации в процессе производства базальтовых волокон 15–25% базальтового расплава не попадает в готовое изделие — холст из базальтовых волокон. Возникает необходимость утилизации отходов производства или использования их в качестве сырья при создании новых композиционных материалов и изделий на их основе.

Выводы

Дано обоснование процесса волокнообразования с помощью дутьевой головки. Получены соотношения, устанавливающие зависимость скорости деформации в струе волокна в зависимости от вязкости расплава.

Получены экспериментальные данные, по которым можно оценить влияние месторождения базальтов на зависимость скорости деформации от вязкости базальтового расплава.

Установлено, что высокоскоростная деформация расплава сильно влияет на качество волокон и на количество отходов при производстве волокон.