Влияние инвестиций и прямых инновационных затрат на оптимальные стратегии развития региона с учетом экономических ущербов от экологических нарушений

В настоящее время инновационная деятельность представляет собой важнейший фактор развития, который должен находить отражение во всех расчетах, связанных со стратегическим планированием. Однако по имеющейся официальной статистике практически невозможно оценивать инновационные процессы в регионе в терминах «затраты-результаты», что необходимо для подобных расчетов.

В типичных официальных документах, отражающих инновационную деятельность в том или ином регионе РФ, она оценивается в таких показателях, как «количество инновационно активных предприятий с общей численностью персонала», «объем инновационной продукции», «процент инновационной продукции, осваиваемой промышленностью», «затраты на инновации разных видов» (технологические, маркетинговые, организационные) (см., например, [1]), что больше подходит для качественной оценки картины, чем для конкретных прогнозных и оптимизационных расчетов. Более полезными в этом плане могли бы быть отчеты предприятий о проведенных инновационных мероприятиях, однако систематизированной информации по ним нет, а изучение разрозненных случайных источников с этой точки зрения требует трудоемких исследовательских работ, тем более что пока не существует общепринятых измерителей инновационной деятельности и даже установившейся терминологии в этой области.

Это затрудняет стратегическое планирование развития даже в чисто экономическом плане, не говоря уже об устойчивом развитии с обоснованным учетом экологических и социальных факторов. В статье предлагается своего рода нормативный подход к этой проблеме с использованием концептуальной модели региона [2,3]. Он состоит в том, что по имеющимся надежным эмпирическим оценкам одних параметров и балансовым и оптимизационным соотношениям модели можно получить оценки предельных значений других параметров.

Модель отражает инновации через видоизменение созданной ранее, в каком-то смысле традиционной, модели региона [4] путем дополнения ее специальным блоком, описывающим инновационные процессы. При этом понятие «инновация» трактуется формально как любое целенаправленное изменение параметров исходной модели, которые прежде рассматривались как константы. Такая схема была предложена в работе [5] и успешно использована при практическом моделировании развития ряда конкретных регионов [2].

Данная статья является продолжением работы [6] и посвящена поиску предельных значений важнейших параметров, относящихся к инновационным процессам, или их приемлемых диапазонов путем организации целенаправленных вычислительных экспериментов с этой моделью. Ее специфика позволяет получить путем специальных преобразований простые соотношения, что важно при проведении серийных расчетов. Эта процедура применяется к агрегированной версии модели [7], которая, с одной стороны, вполне отвечает поставленной цели, а с другой — достаточно наглядна. Однако при естественных предположениях она может быть распространена на региональные модели того же типа любой размерности.

1.    Агрегированная модель и магистральное решение

Рассматривается модель с инновационным блоком, которая выражается следующими соотношениями:

с = (1 - A ) y - Bu - Az - A^akd ,                                                             (1)

k = u - 5k , 0 <  y <  g ( k , L ), r = r + N ( r - r ( t )) - Cy + z ,

9 = 1 d + HuXo ( t ) - 9 ) 9(0) = 0.

Здесь y , z , d – соответственно выпуск продукции, темп активного природовосстановления и темп активных инноваций; с – конечное потребление; k , g ( k , L ) , u , δ – соответственно основные фонды, мощность, инвестиции и темп амортизации; L – население (предполагается, что трудовые ресурсы, от которых фактически зависит мощность, пропорциональны населению); A , A^z , A^d – соответственно коэффициенты прямых затрат в производственном, природовосстановительном и инновационном секторах; B – коэффициент фондообразующих затрат; r – индекс состояния природной среды и ресурсов; r ( t ) – заданная функция (опорная), например, получаемая из статистического прогноза; N , C – коэффициенты самовосстановления и прямого воздействия экономики на природную подсистему; θ – инновационный индекс, имеющий смысл среднего процента инновационных изменений некоторой группы параметров (в данном случае A и C ) относительно их значений в начальный момент времени; θ ( t ) – значение θ , соответствующее мировому уровню в данный момент; H – коэффициент, отражающий влияние инвестиций, связанных с расширением производства.

Его смысл легко выясняется, если положить d = 0 . Это процентное изменение в среднем рассматриваемой группы параметров при изменении основных фондов на 1%. Аналогично выясняется смысл величины d как скорости процентного изменения рассматриваемой группы параметров при отсутствии инвестиций и затем — параметра A^d как затрат на 1% инновационных изменений, приходящихся на единицу основных фондов.

Предполагается, что g ( k , L ) – классическая вогнутая по k , L – производственная функция, k >  0, r >  0, d >  0, природовосстановительная и инновационная деятельность ведется на существующих мощностях с неограниченной интенсивностью и требует лишь дополнительных прямых затрат.

Предполагается также, что коэффициент прямых затрат A растет с ухудшением экологической ситуации (уменьшением r ), однако может быть снижен за счет инноваций (роста θ ) вместе с другим важным параметром – коэффициентом отрицательного воздействия производства на природную среду C , т.е. будем эти коэффициенты рассматривать как функции A ( r , θ ) и C ( θ ) с указанными свойствами. Остальные коэффициенты для простоты принимаются константами.

Поставим задачу оптимального управления, в которой переменные y , u , z и d играют роли управлений, а в качестве критерия оптимальности (называемого функционалом благосостояния) рассматривается максимум накопленного регионального дохода за вычетом штрафа s ( r ) за экологические нарушения на заданном временном интервале при заданных начальных условиях:

tF

П= | ( pc - s ( r )e ^{p t}dt , k (0) = k ₀, r (0) = r ₀, 9(0) = 0

где p – прогнозируемая цена (ценовая поправка), ρ – коэффициент дисконтирования. Величина штрафа характеризует предпочтения в критерии благосостояния.

В [7] находится магистральное решение как простое идеализированное при указанных предположениях, которое затем и исследуется в вычислительных экспериментах. Приведем кратко процедуру его нахождения.

Для удобства 9 заменяется новой переменной у = H ln k + ln( 9 - 9 ), тем самым упрощается связь

(4):

Y = - ( d + H5 ), y (0) = H ln k ₀ + ln( 9 ),

Вначале получается семейство решений при любых фиксированных конечных значениях k ( t_F ) = k F , r ( t_F ) = r_F , y ( t_F ) = Y F = H ln k_F + ln( 0 - ^_F ), а затем эти значения варьируются и тем самым находится окончательное решение. В силу заданных дифференциальных связей и ограничений на d и k получаются естественные верхняя () _u и нижняя () _l границы изменения искомых функций ^k ( t ), r ⁽ t ) и у ⁽ t ): k_u = k F >  k ( t ) >  k , = k o , r_u = r F >  r i = r o , y _u = у о - H 5 t >  у ⁽ t ) >  Y i = Y f ^- H 5 ⁽ t ^- t F ) (рис. 1).

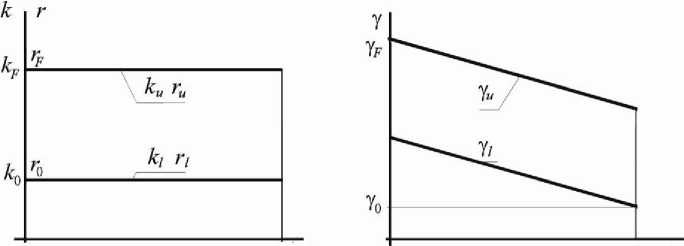
0                                t_F t о                                i_F t

Рис. 1.

В соответствии с теорией вырожденных задач [8] управления u , z принимаются неограниченными и производится двукратный переход к эквивалентной производной задаче первого порядка о максимуме функционала П _F с использованием преобразований x = П + p ( A^zr + Bk ), ^ = x - pA d k₀у . Функционал максимизируется вначале при любых фиксированных граничных значениях k_F , r_F , и

γ _F , а затем дополнительно максимизируется по этим значениям.

Коэффициенты A , B и C задаются следующим образом:

A = (1 - a0 ) b ( r ) A 0 , C = (1 - (1 - a)0 ) C 0 , 0 <  а <  1,

b ( r ) = 1 - b 1 ( r - r ) + b ₂( r - r ) 2 , b 1 , b 2 >  0, а выбирается из условия максимума П _F , B = B ₀ + b 3 H . Предполагается L = const , при этом g ( k , L ) = qk ^a (функция Кобба-Дугласа), s ( r ) = s ( r - r ) 2 , 0 = const , p = 0 , p = const = 1.

С учетом этих предположений и при естественном условии рентабельности экономики дело сводится к задаче максимизации выражения:

1 - e^H ^ ^F

--+

Hδ

r ^{)2) -} A ^{( r - r} 0 )

П _F = t_F ( к 1 qk ^a - B5k ) - B ( k_F - k ₀) + pqk “ ^{- H}e ^Y

+ Adk0(Yf - Y0 + H8 tF) + tF (AZN(r - r) - s(r - при условии k > k0, r > r0, у < Y0 - H5 tF относительно k , r и у , которые в данном случае обозначают конечные значения kF, rF и yf (индекс F для краткости опущен). Здесь к1 = X + ц0 , X = 1 - A0 - AZC0, ц = max(A0, AZC0).

Рассматриваемая функция вогнута относительно k , r , γ . Ее максимум по этим переменным достигается в стационарной точке, определяемой условиями

дП = дП = дП = 0 dk dr Эу

либо на границе.

В общем случае для произвольных значений α и H и ненулевых коэффициентов b1 и b2 решение в аналитической форме найти не удается. Однако его нетрудно получить численно посредством несложных дополнительных улучшающих итераций для исходного выражения (7). Поскольку функционал (7) рассматривается без дифференциальных связей, то процедура его улучшения оказывается по существу конечномерной. В общем случае решение нетрудно получить численно перебором по трем переменным.

2.    Вычислительные эксперименты

Расчеты проводились для условного региона со значениями параметров, генерированными по данным Байкальского региона (табл. 1).

Таблица 1

Параметр	Значение	Параметр	Значение	Параметр	Значение
tF	20	p	1	A 0	0.5
A ( r , θ )	(1 - a θ ) b ( r ) A 0	C 0	0.7*10-5	C ( θ )	(1 - (1 - a ) θ ) C 0
B 0	1	Az	8000	δ	0.05
k 0	400	k F	800	θ 0	0
θ F	0.75	θ	0.8	r 0	0.8
rF	0.9	r	1	N	-0.001
s	100,1200,1500	α	0.5,0.7,0.8	q	10,2.2,1.1

Рассматривались максимальные значения Π _F при различных значениях параметров A^d , H , B , b ₁ и b ₂ , нескольких вариантов параметров экономики α и штрафа s . Расчеты проводились с помощью программного пакета Maple 15 на ПК с 32-разрядным ЦП с частотой 2.7 Гц, ОЗУ 4 Гб. Результаты представлены в форме семейств зависимостей Π _F ( A^d ) и Π _F ( b ₁) .

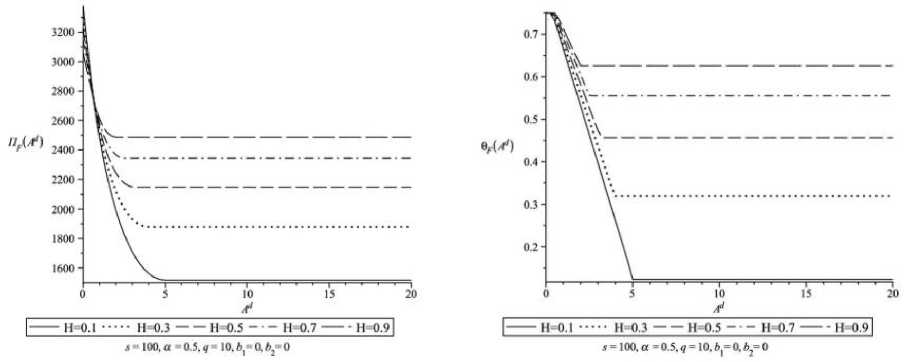
Рис. 2.

Из результатов, представленных на рис. 2-7, можно сделать следующие выводы:

• 1)    определяются предельные значения удельных текущих инновационных затрат A ^d , при превышении которых инновационная деятельность становится неэффективной и прекращается (функционал благосостояния не меняется);

  

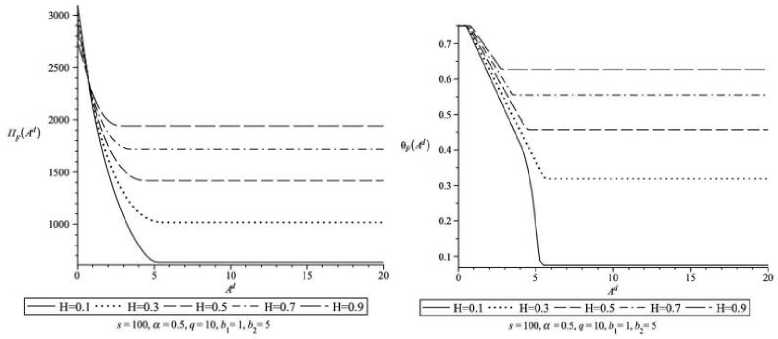
  Рис. 3.

  
  
  

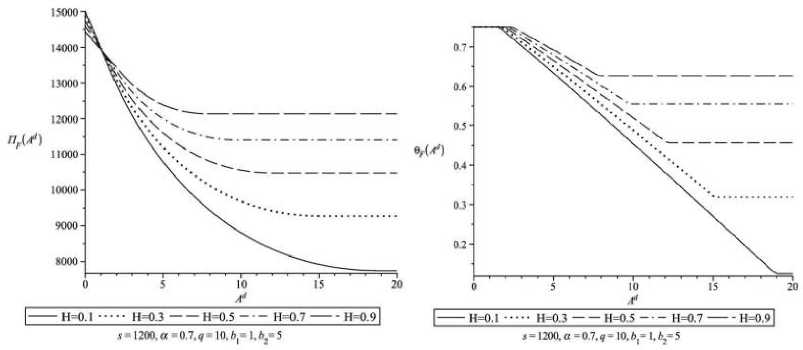
  Рис. 4.

  
  

• 2)    приемлемые значения существенно зависят от фондоотдачи, характеризуемой параметром α , и мало зависят от коэффициента s , характеризующего предпочтения в критерии благосостояния;

• 3)    существует критическое значение A^d (единое для всего семейства как точка пересечения соответствующих графиков), ниже которого более выгодна текущая инновационная деятельность, а выше – инновационная деятельность, связанная с инвестициями;

• 4)    результирующие значения целевого функционала Π _F и инновационного индекса θ растут с увеличением H ;

• 5)    с ростом A^d отмечается резкое падение эффективности инноваций: снижение инновационного индекса θ и Π _F ;

  
  
  
  
  
  

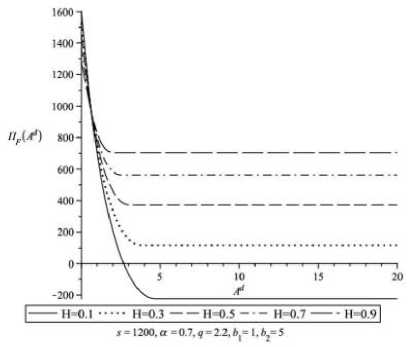
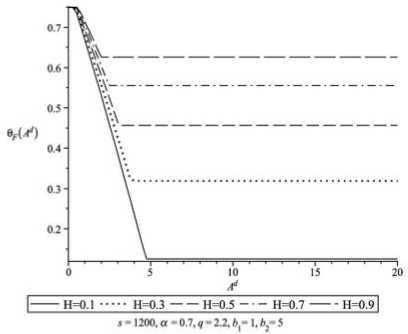
Рис. 5.

• 6)    при усилении зависимости A от r (рост b ₁ ) результирующее значение функционала благосос-

  тояния Π _F уменьшается, а инновационный индекс θ растет.

  
  
  
  
  
  

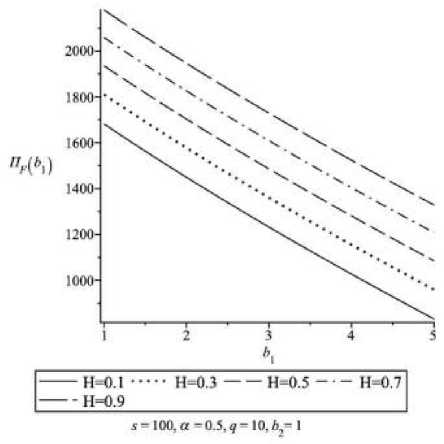
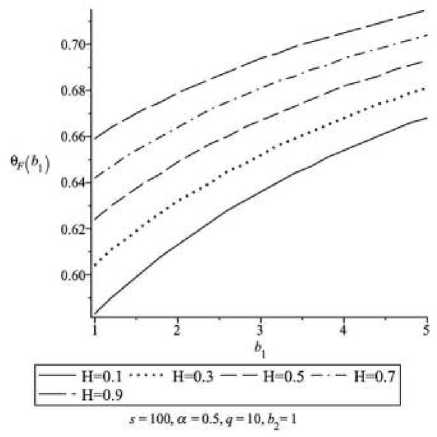
Рис. 6.

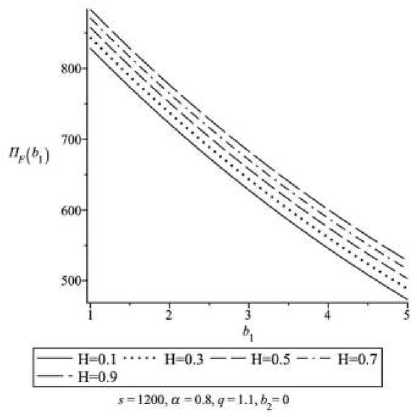
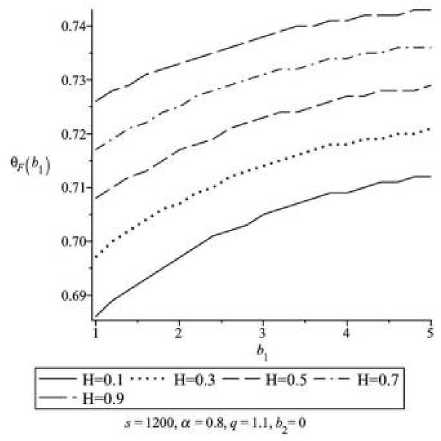
Рис. 7.

Заключение

В целом можно утверждать, что предложенный нормативный подход к оценке экономической эффективности инновационных процессов себя оправдал. При этом важную роль играет именно наиболее агрегированная версия региональной модели, в которой матричные коэффициенты, содержащие большое число параметров, сводятся к числовым коэффициентам, допускающим достаточно простую содержательную интерпретацию.

Другой важный методический аспект — возможность получения простых расчетных соотношений для быстрых серийных вычислительных экспериментов исходя из специфики рассматриваемой задачи как вырожденной задачи оптимального управления. Соответствующая процедура преобразований непосредственно распространяется на многокомпонентные модели любой размерности, что дает возможность получить эффективный инструментарий для более детальных оценок с использованием данного опыта.

Г.В. Попков. Модель перспективной транспортной сети связи Российской Федерации