Влияние изменения модельных коэффициентов модели турбулентности k-w SST Ментера на параметры обтекания аэродинамического профиля

Введение. В инженерной практике исследований аэродинамического обтекания летательных аппаратов (ЛА) широкое распространение получила двухпараметрическая модель турбулентности k-ω SST Ментера ( MSST ) [1, 2]. Ее преимуществами являются вычислительная экономичность, широкий диапазон исследуемых задач и в целом приемлемая точность [3]. К недостаткам следует отнести проблемы с описанием отрывных течений, характерных для обтекания ЛА на закритических углах атаки [3–7].

Эту проблему позволяет решить гибридная модель турбулентности DES (Detached Eddy Simulation) [2], недостатком которой являются значительные вычислительные затраты, что делает ее малоприменимой для решений инженерных задач [4, 5].

В основе модели турбулентности MSST лежат два уравнения (1, 2), включающие набор эмпирических коэффициентов (табл. 1), значение которых подобраны по результатам натурных экспериментов [1, 2].

Улучшение результатов описания отрывных течений с использованием модели MSST посредством коррекции этих коэффициентов предположительно позволит увеличить точность без роста вычислительных затрат.

Таблица 1

Эмпирические коэффициенты модели турбулентности MSST

O -fcl	с ю l	^ k-z	o-toz	Pi		∗	Cl-^	к
0,568	0,5	1	0,856	0,075	0,0828	0,09	0,31	0,41

В статье [8] представлены результаты варьирования модельного коэффициента a 1 для улучшения результатов моделирования отрывных течений на примере исследования обтекания ряда несимметричных аэродинамических профилей.

Целью работы, представленной в настоящей статье, является оценка влияния изменения коэффициента a 1 модели турбулентности MSST на распределение коэффициентов давления по поверхности симметричного профиля NACA 0012 [9, 10].

Расчетная схема и методы исследования. Модель MSST базируется на двух уравнениях: для турбулентной кинетической энергии k (1) и скорости диссипации энергии ω(2) [1, 2].

д (рк)   ^{д (}Р^ки j )

+       = τ д t     д x

д k

д U         , д z ,      _х к к

— Рр^юк+— ( р+О к g _t )— .

д Xj          д Xj            д Xj

S X-

д(рю)^д(ркиj) _ ур

д t     д x

= τ

А

д ю

д и, _{п 2} д ₍        х д ю _ /.   „ .

ij^ ₽ 2 р^ю +^ (Р+°<Л)— +2 (1 ^- F 1 ) д Xj          д Xj

д x

р° ю2 д к д ю ю   д Xj д Xj

.

Входящие в состав модели функции и константы:

y = ^в - ^fr ; F =^tanh ( ^{ar g} i ) ; F 2 =^tanh ( ^{ar g} 2 ) ; arg 2 =^{max e}  v e

' 2Vk 500 ' _к 0,09юу; у² ю _v

;

arg^ = min max к

/к 500 \ 4ро_Ю 2 к

к 0,09юу ;у² ю J ;CD_kB у²

;

;CD = max 2ρσ kω

V

• 1    д к д ю

;10 ω2

ю дx- дx-

-20

;

• (2)

• (3)

^k = F1^k 1 + (1 - F1)^k 2;^» = Fi^n + (1 - F1)^i 2;в = FiPi + (1 - FW

Турбулентная вязкость в соответствии с гипотезой Буссинеска для MSST выражается зависимостью:

Pt = р--- max

k

SF a1

где p - плотность; u - скорость; ц - динамическая вязкость; у - расстояние до стенки; v - кинематическая вязкость; τ – касательные напряжения; S – скорость деформации.

Значение модельных констант представлено в табл. 1.

Рассмотрено обтекание профиля несжимаемым потоком – с числом Маха М = 0,13 и числом Рейнольдса Re = 3^.10⁶.

Сеточная модель расчетной области гексагональная, блочно-структурированная (рис. 1). Дискретизация в пограничном слое проведена из ограничения для низкорейнольдсовых RANS- моделей Y ⁺< 3 [1, 2, 7, 11].

Рис. 1. Сеточная модель расчетной области для модели турбулентности MSST

Решение системы дифференциальных уравнений произведено с использованием схемы второго порядка точности в трехмерной стационарной постановке [2].

Для валидации ряда полученных параметров проведен расчет обтекания профиля с использованием гибридной модели турбулентности DES ( LES-MSST ) [2], набор модельных коэффициентов принят стандартным (см. табл. 1).

Сеточная модель расчетной области для модели турбулентности DES построена на основе сетки для MSST с учетом ограничений: Y ⁺< 1, X ⁺< 10, Z ⁺< 20 (рис. 2) [2, 12]. Постановка задачи трехмерная, нестационарная.

Рис. 2. Сеточная модель расчетной области для модели турбулентности DES

Для решения задачи обтекания с использованием модели турбулентности DES использованы ресурсы суперкомпьютера «Торнадо», ЮУрГУ.

Проведена оценка независимости решения от размерности сетки. При систематическом измельчении размера элемента сетки MSST проведен контроль за изменением коэффициента подъемной силы для угла атаки а = 10 ° . Результаты представлены на рис. 3.

Сy 1,04

0,96

0,92

0,88

100       150

200       250       300       350       400

Число элементов, тыс

Рис. 3. Зависимость коэффициента подъемной силы от размерности сетки

Контрольный параметр сходится при систематическом измельчении сетки, что указывает на независимость решения от размерности сетки. В табл. 2 представлены параметры построенных сеток.

Таблица 2 Параметры построенных сеток

Используемая модель турбулентности	Число элементов, тыс	Число элементов на поверхности профиля	Размах крыла, м
MSST	364	700	1
	300	560
	246	400
	197	340
	170	240
DES	3000	450	0,05

Результаты численного моделирования. Достоверность моделирования течения в пограничном слое проведена посредством сравнения безразмерного профиля скорости с «функцией стенки» – полуэмпирической аппроксимированной зависимостью [13] (рис. 4). Сравнение проведено для случая обтекания с углом атаки α = 0 в сечениях на расстоянии 0,15, 0,4 и 0,6 длины хорды от передней критической точки профиля.

U+ (безразмерная скорость)

x/c = 0.15

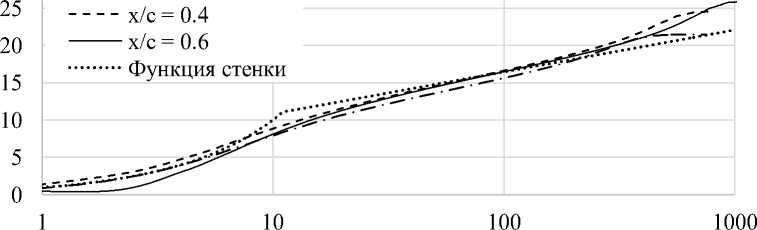
Y+ (безразмерное расстояние до стенки)

Рис. 4. Сравнение безразмерного профиля скорости с функцией стенки в сечениях профиля NACA 0012

Моделируемый профиль скорости имеет удовлетворительное совпадение с функцией стенки. Качество моделирования течения в пограничном слое подтверждено.

Характерным параметром, отражающим качество моделирования обтекания авиационного профиля, является распределение коэффициента давления по поверхности профиля [9, 10, 14, 15].

В публикациях [16–20] содержатся результаты экспериментальных исследований профиля NACA 0012 в аэродинамических трубах для используемых в настоящей статье значений числа Рейнольдса. Несмотря на реализацию несжимаемого течения (число Маха M < 0,3), распределения значений коэффициентов давления по поверхности профиля для каждой из указанных публикаций различны. Для валидации модели, исследуемой в настоящей статье, использованы материалы, представленные в публикации [16] как имеющие наилучшее совпадение с моделью турбулентности DES .

На рис. 5–7 представлено сравнение расчетных распределений коэффициента давления по поверхности профиля с экспериментальными данными [16] для различных углов атаки при варьировании коэффициента a 1.

Cp -0,80

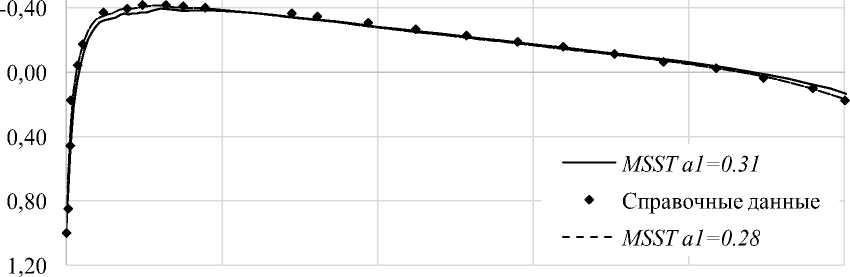
0,2              0,4              0,6              0,8

Рис. 5. Сравнение расчетных распределений коэффициента давления по поверхности профиля с экспериментальными данными [16], угол атаки α = 0

1 x/c

Наблюдаются незначительные улучшения распределения коэффициента Cp для угла атаки a = 0 при a 1= 0,28.

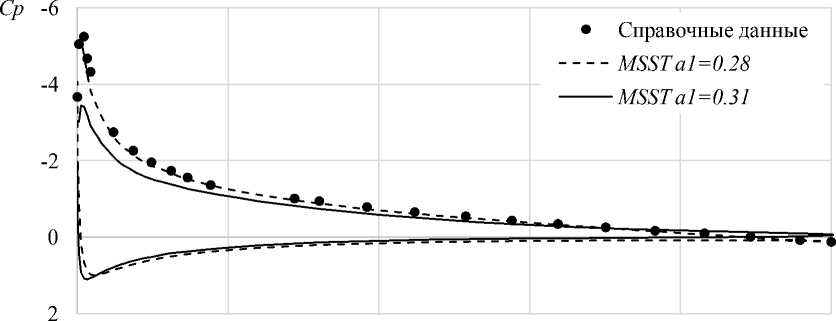
0               0,2              0,4              0,6              0,8               1 x/c

Рис. 6. Сравнение расчетных распределений коэффициента давления по поверхности профиля с экспериментальными данными [16], угол атаки а = 10 °

Для угла атаки a = 10 ° наблюдаются значительные расхождения стандартной модели MSST с экспериментом ( a 1 = 0,31). При этом уменьшение значения коэффициента a 1 на 30 %, в соответствии со статьей [8] ( a 1 = 0,28),значительно улучшает результаты моделирования.

Для угла атаки a =15 ° дополнительно проведен расчет с использованием модели турбулентности DES .

Cp -12

MSST а1=0.31

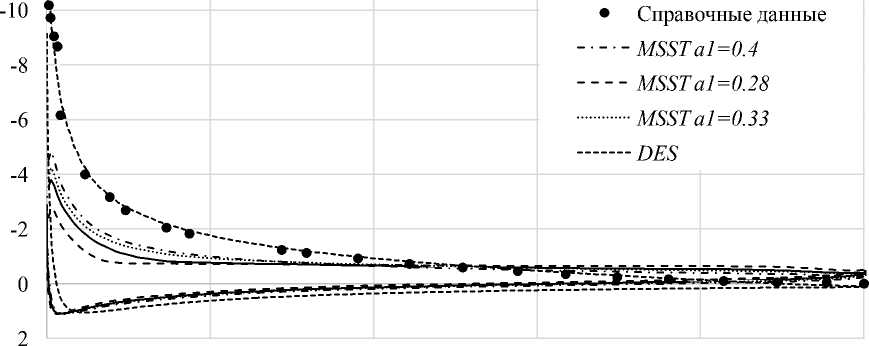
0                 0,2                0,4                0,6                0,8                 1

x/c

Рис. 7. Сравнение расчетных распределений коэффициента давления по поверхности профиля с экспериментальными данными из [16], угол атаки а = 15 °

Угол атаки a = 15 ° является для профиля NACA 0012 закритическим, что определяет наличие отрывного обтекания. При этом стандартная модель MSST дает значительные расхождения с экспериментом. Уменьшение значения коэффициента a 1 сопровождается увеличением расхождения.

Высказана гипотеза о возможности улучшения результатов моделирования посредством увеличения значения коэффициента a 1.

Для проверки гипотезы значение коэффициента последовательно было увеличено до значения a 1 = 0,4. При этом отмечено незначительное улучшение результатов моделирования.

Увеличения коэффициента на более значительные величины нецелесообразны, так как даже в малом изменении влекут нарушение калибровки модели турбулентности MSST , что отмечено в статье [8].

Выводы

• 1.    Для докритических углов атаки уменьшение значения коэффициента a 1 значительно улучшает результаты моделирования.

• 2.    Закритические углы атаки характеризуются отрывным течением, для которого уменьшение значения a 1 ухудшает результаты моделирования, а увеличение дает незначительное улучшение.

• 3.    Эти результаты отличаются от представленных в статье [8], для которых авторы однозначно дают заключение об улучшении результатов в диапазоне углов атаки а = 0.. .30 ° .

Обсуждение и применение. Как показали исследования, изменение коэффициента a 1 на за-критических углах атаки не позволяет значительно улучшить результаты моделирования отрывных течений. Более того, как указано в статье [8], такой подход ломает калибровку модели, что ухудшает результаты расчета других параметров (например, распределение касательных напряжений по поверхности профиля). Этот фактор является приемлемой ценой для докритических углов атаки: незначительное ухудшение описания касательных напряжений против заметного улучшения распределения давления. Для закритических углов такой подход неприемлем, так как улучшения точности не наблюдается.

Дальнейшие исследования следует направить на изучение причин расхождения результатов настоящего исследования с результатами статьи [8] для закритических углов атаки и поиску решения по восстановлению калибровки модели MSST при варьировании коэффициента a 1.