Влияние изменения сечения наноканалов на их электрогидродинамические характеристики

Электрокинетические процессы в последнее время привлекают большое внимание в связи с бурным развитием микро-, нано- и биотехнологий. Одно из важных как с практической, так и с фундаментальной точки зрения гидродинамических течений, где проявляются новые эффекты при взаимодействии с электрическим током — это течение раствора электролита в тонких каналах с заряженными стенками под действием разности потенциалов и давлений. Классическая теория течения в микроканалах основана на предположении об электронейтральности раствора электролита вне тонких двойных электрических

(дебаевских) слоёв (ДЭС) [1, 2]. Толщина ДЭС, в зависимости от концентрации раствора, меняется от 1 до 100 нм, а ширина типичного микроканала составляет 1–100 мкм. Такое соотношение размеров позволяет упростить задачу и уйти от решения связанной системы уравнений Нернста–Планка, Пуассона и Навье–Стокса к решениям на разных масштабах, то есть из решения задачи в ДЭС найти скорость скольжения на внешней границе дебаевского слоя и использовать эту скорость в качестве краевого условия для решения внешней — электронейтральной — задачи (см., например, [3, 4]). Внешняя задача описывается уравнениями Навье–Стокса (обычно в приближении ползущего течения), уравнением диффузии-конвекции концентрации соли и уравнением распределения потенциала [2]. Под действием разности потенциалов возникает объёмный электрический ток, подчиняющийся закону Ома, в котором концентрация соли определяет электрическую проводимость. Решение линейного уравнения диффузии составляет теоретическую основу для стандартных экспериментальных методов, таких как хронопотенциометрия (реакция напряжения Санда на скачок тока [5]), спектроскопия электрохимического импеданса (импеданс Варбурга для воздействия переменным током [6]).

В ряде случаев возникает необходимость в решении системы уравнений Нернста–Планка, Пуассона и Навье–Стокса (обычно в приближении Стокса) без вышеуказанных упрощений. Так в [7] это необходимо для описания эффекта концентрационной поляризации вблизи электродов и/или ионообменных мембран, а также при электрофорезе заряженных гранул. Концентрационная поляризация связана с существованием нормального к поверхности раздела фаз электрического тока. Её экспериментальному и численному исследованию посвящены, например, работы [8, 9].

Менее известным, но набирающим популярность направлением является изучение тангенциального электрического тока в микро- и наноканалах, при электрофорезе и других процессах электрокинетики. В случае увеличения напряжённости и/или уменьшения характерного размера ток перестаёт быть только объёмным, так как вклад поверхностного тока в слое Дебая становится существенным [10]. Соответственно, такие течения сопровождаются новыми физическими эффектами, находящими широкое практическое применение, в частности, для создания компактных устройств обессоливания морской воды, разделения макромолекул. На стыке микро- и наноканалов возникает интересный эффект суперконцентрации [11, 12], который в медицине может быть инструментом для ранней диагностики ряда заболеваний.

Исследование течений в наноканалах сталкивается со многими теоретическими сложностям. Например, для описания явлений переноса и электростатики вместо уравнений Нернста–Планка и Пуассона иногда используется другая формулировка [13], причём её эквивалентность упомянутой ранее постановке не исследована. Другая принципиальная сложность связана с вопросом границ применимости гипотезы сплошной среды, согласно которой все рассматриваемые величины (плотность, скорость, давление и другие) предполагаются определёнными всюду в пространстве и непрерывно изменяющимися от точки к точке в пределах рассматриваемой области. Ответ во многом зависит от конкретики задачи, в частности, требуется, чтобы характерные размеры изучаемого объекта были достаточно большими. Грубые оценки, которые восходят ещё к Прандтлю и повторяются многими авторами (например, см. [14]) дают для капельных жидкостей величину 10 нм, а для газов — 1 мкм. Более точный современный анализ, основанный на сравнении результатов континуального подхода и подхода молекулярной динамики [15], уточняет предельную длину для жидкостей до 50 нм. Исследования на основе молекулярной динамики [16] говорят, что уравнения Навье–Стокса можно применять и для размеров порядка 6 нм, если модифицировать выражения для вязкости. Родственной вязкости величиной является диффузия. Чтобы вязкость и диффузия были непрерывными, необходимо более частое взаимодействие молекул друг с другом, а не с границами области. Сужение области приводит к нарушению этого требования, и коэффициенты диффузии [17], как и коэффициенты вязкости, в направлениях, перпендикулярных стенкам, должны быть существенно меньше, чем коэффициент диффузии вдоль канала.

Ещё одна особенность течения в объектах малых масштабов — это проскальзывание жидкости на твёрдой границе, которое может кардинально изменить транспортные свойства потока. В таком случае на поверхности исчезает только нормальная составляющая скорости, а тангенциальные компоненты U _s пропорциональны своим нормальным производным: U _$ = B d U _$ /д п , где B — длина скольжения Стокса, которая зависит от свойств поверхности и меняется в диапазоне 0 <  b <  100 нм [18]. Недавний большой обзор, посвящённый проскальзыванию, можно найти в [19].

Теоретические сложности возникают и при рассмотрении электростатической составляющей задачи. В большинстве подходов поверхностная плотность заряда считается постоянной [2], однако в экспериментах [20] установлена её сильная зависимость от концентрации раствора электролита. Более того, в [20] для исследования электрического потенциала в наномасштабах учитываются размеры ионов, что предполагает замену оператора Лапласа в уравнении Пуассона оператором четвёртого порядка и введение дополнительных краевых условий. Более подробный обзор особенностей течений в наноканалах выходит за рамки данной работы. В заключение скажем, что порой работы противоречат друг другу и, следовательно, течения в наноканалах требуют дальнейших исследований.

Во многих теоретических подходах используется постановка задач в рамках системы уравнений Нернста–Планка, Пуассона и Навье–Стокса без учёта вышеперечисленных особенностей. В настоящей работе используется континуальный подход, однако впервые оценивается возможное изменение результатов при модификации выражения для коэффициентов вязкости, диффузии и длины Стокса согласно выводам на основе молекулярной динамики [15, 17–19].

Численно в полной постановке задача течения в наноканалах решалась в работах [21, 22]; обнаружены «концентрационные скачки», напоминающие ударные волны газовой динамики. Этот результат имеет не только важное фундаментальное (особенно для механиков, как типичное проявление нелинейности), но и практическое значение. Авторы [21, 22] высказали предположение, что при добавлении ионов третьего типа в этих скачках возможно локальное сосредоточение образующегося тернарного электролита. Это объясняло бы так называемый эффект суперконцентрации, найденной экспериментально в [11, 12]. Следует подчеркнуть, что в настоящее время нет ни убедительного подтверждения, ни опровержения этой догадки.

В слабонелинейном приближении задача сводится к одномерной в работах [23], [24], но при этом вводится много ограничений для её упрощения: слабая нелинейность и малые числа Дебая, то есть модель в принципе не может учитывать, что ДЭС могут перекрывать друг друга. Кроме этого, модель [24] не учитывает механизм переноса ионов посредством адвекции, а принимает во внимание только диффузию и электромиграцию. Для большинства практических приложений наноканалы существенно длиннее своей ширины. Для таких каналов задача, описываемая уравнениями Нернста–Планка, Пуассона и Навье–Стокса [21, 22], с одной стороны, с трудом поддаётся как численной реализации, так и обобщению на тернарный электролит, не говоря уже о том, что сложные численные модели не дают возможности понимания физики течения электролита в наноканале. С другой стороны, упрощения аналитических подходов [23, 24], по-видимому, являются не вполне обоснованными, так как результаты этих работ плохо согласуются с результатами из [21, 22].

В данной работе предложена новая простая модель течения в наноканалах переменного сечения, преодолевающая эти недостатки. Тот факт, что изменения вдоль наноканалов происходят значительно медленнее, чем поперёк их, позволяет ввести малый параметр, воспользоваться асимптотическим подходом и вывести систему одномерных уравнений без допущений слабой нелинейности, малости числа Дебая и других, используемых в [23] и [24]. При этом толщина ДЭС может быть как сопоставимой с шириной наноканала (поэтому в нём может происходить перекрытие дебаевских слоёв), так и намного меньше её. В силу малости чисел Рейнольдса, динамика течения рассматривается в приближении Стокса. Сравнение решений по предлагаемой модели с [21, 22] дает разумное соответствие. Модель относительно легко обобщается на течение тернарного электролита. Таким образом, настоящий подход создает задел для исследования более сложных микро-/нанофлюидных систем.

2.    Постановка задачи

Рассматривается осесимметричное течение бинарного одновалентного электролита в плоском канале переменного сечения (Рис. 1) с электрически заряженными стенками под совместным действием разности потенциалов и давлений.

При ширине канала в диапазоне 50–150 нм

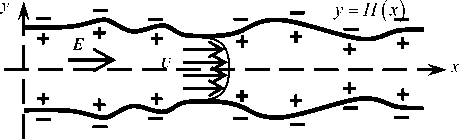
Рис. 1. Схема течения электролита в осесимметричном наноканале переменного сечения

половина ширины канала на входе h ₀ ; для времени

движение электролита описывается уравнениями Нернста–Планка для   транспорта ионов, уравнением Пуассона   для распределения электрического потенциала и уравнениями Навье–Стокса для течения жидкой фазы [15]. Уравнения Навье–Стокса, в силу малости характерных чисел Рейнольдса, записываются в приближении   ползущего   течения. Все параметры задачи обезразмериваются. В качестве характерных величин берутся: для длины — h02 D (здесь D — коэффициент диффузии ионов;

в силу симметрии объёма электролита коэффициенты диффузии катионов и анионов равны); для скорости — Dih0 ; для динамического поведения системы — динамическая вязкость жидкости ц. Втекающий электролит принимается электронейтральным, концентрации катионов и анионов отнесены к концентрации электролита на входе — C0 . Характерным потенциалом служит термический потенциал Ф0 = RT/F, где R — универсальная газовая постоянная, F — постоянная Фарадея, T — абсолютная температура, которая предполагается неизменной.

Безразмерные уравнения имеют следующий вид:

ЭС ⁺      .              _ _

-— + v- j+= 0, j+= UC+ — C+VФ — V C+, dt — rC- + v- j—= 0, j—= UC"+ C "VФ —V C -, ,,

2 e ² V ² Ф = C

f—

C ⁺ ,

V2U = VP — кVФV2Ф ,   VU = 0.

Здесь: t — время; C ⁺ и C — концентрации катионов и анионов соответственно; U = ( U , V ) — вектор скорости, Ф — потенциал электрического поля; Р — давление; е = Х D /h 0 , где X D = ^d Ф ₀/0 c ₀ F — длина Дебая (расстояние, на которое распространяется действие электрического поля отдельного заряда); к = d Ф 0 ^ D — коэффициент связи гидродинамических и электростатических величин (далее — коэффициент сцепления), где d — диэлектрическая проницаемость среды, полагаемая неизменной. Коэффициент сцепления заменяет число Пекле, которое при выбранном нормировании равняется единице.

Задаются следующие граничные и краевые условия:

• -    на жёстких боковых стенках у = ± H ( x ) — условия прилипания и непротекания жидкости, непроницаемость стенок для катионов и анионов, скачок потенциала на заряженной стенке

U = 0,    j ⁺- n = j ^—- n = 0,    еУФ- n = —с ,                              (4)

где n — вектор нормали к поверхности стенки, с — плотность поверхностного заряда;

– на входе в канал — условие

C+ = C - = 1, которое согласуется с выбранным нормировочным множителем; – на выходе — «мягкое» граничное условие дC+ _8C - =0 дx ” дx ~ ’

• -    в начальный момент времени t = 0 концентрации неизменны во всех точках канала

3.    Асимптотический метод получения упрощённых уравнений

C ⁺ = C ^-= 1.

Краевые условия на потенциал и скорость будут рассмотрены в разделе 4.

Рассмотрим канал, длина которого намного больше среднего значения его ширины, в предположении, что характеристики течения в тангенциальном направлении эволюционируют медленнее, чем в нормальном: д/д x << д/д у . Это даёт возможность использовать для решения системы уравнений (1)-(4) интегральный метод, например, метод Кармана–Польгаузена [25].

Сделаем первый шаг: пренебрегая малыми изменениями потенциала в тангенциальном направлении, с учётом электромиграции и диффузии только в нормальном направлении приведём уравнение Пуассона (2) к виду:

0= 0 ^Ф- C -ду ⁰

—

C ⁺.

Это упрощённое уравнение имеет следующее решение:

Ф =

с ch (у4С/е)

V c sh ( hJC /е ) ’

C+ = C

г1—

^С ch ( у4с /е)

V c sh ( h4c Ц,

C ^— = C

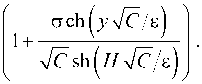
Здесь C является медленно меняющейся функцией переменных x и t : C = C ( x , t ) . Решение (5) справедливо при с <<  1 вне зависимости от порядка е . Для наноканалов е = O ( 1 ) и имеет место перекрытие дебаевских слоёв; для микроканалов е <<  1 и (5) соответствует классическому решению Дебая [2].

На втором шаге рассмотрим уравнения (3), которые при условии д/д x <<д/д у и, следовательно, при V <<  U , принимают вид:

д ⁰ U       д ²Ф_р

—- = П + к—- E, ду0          ду y где П = дР/дx , E = —дФ/дx, U — компонента скорости, быстро меняющаяся функция у , но слабо зависящая от x и t . В силу линейности уравнения (6) эту скорость удобно представить в виде суперпозиции напорной ( Up ) и электроосмотической ( Ue ) частей, каждая из которых по отдельности удовлетворяет краевым условиям по y . Из (6) легко найдём:

U p = ( П/ 2 ) ( y ² - H ²) ,    U e = k E ( Ф-Z ) .

Здесь Z — значение потенциала Ф на боковых стенках y = ± H . Для микроканалов, в которых длина Дебая намного меньше ширины канала, Z приобретает физическое значение дзета-потенциала:

Z —— о/ Сс ,    £ —— 0 .

Напорная и электроосмотическая части скорости создают расходы по сечению канала. В силу симметрии задачи удобно рассмотреть половины этих расходов, соответственно, Q_p и Q_e :

л H³ о г f^e H CH^H

Qn =-П--,  Q, = kE о---;=ch---- p 3              I C JC     £

.

Заметим, что в силу несжимаемости электролита общий полурасход Q = Q_p + Q e является константой.

Наконец, на третьем шаге проинтегрируем уравнения транспорта ионов (1). Воспользовавшись условиями непроницаемости стенок для обоих типов ионов и вынеся дифференциальные операторы из-под знаков интеграла, придём к выражению:

H          H             H         2 H

— [C^±dy + — f UG^±dy ± — E\C ± dy =   f C ± dy - —^f—

5 1 00         d x 0           d x 0         d x ² -'          d x ( d x

Подстановка в (9) найденных выше решений позволяет получить уравнения относительно двух неизвестных функций — C и E , и параметра Q . Соответствующие выкладки опустим, сказав только, что вычитание друг из друга интегральных уравнений (9), записанных для C+ и C-, приводит к уничтожению производной по времени t , а оставшееся обыкновенное дифференциальное уравнение после однократного интегрирования по x переходит в алгебраическое уравнение. Постоянная интегрирования — обозначим её через I — имеет физический смысл электрического тока через канал и определяется из краевых условий L по x (интеграл J Edx равен разности потенциалов между входом и выходом канала). Итоговое

асимптотическое уравнение имеет вид:

-( HC ) + — a t ’ a x

где E = M/N , а М и N задаются соотношениями:

М = 6 Q 8-^fZ H - —) + 2 Z C— + 1 ,    N = -6^ ^f Z H -—¹ +k(o² H + 8oZ- CH Z²) + 2 CH .

h ³ I?     c J      a x               h ³ I c J                     ⁷

Уравнение (10) справедливо для каналов шириной от 50 нм со слабо заряженными стенками. Применение континуального подхода на основе уравнений Навье–Стокса и Нернста–Планка для меньшей ширины канала (вплоть до 6 нм) нуждается в модификации выражения для вязкости и диффузии [16, 17]. Требуется, чтобы они были анизотропными и имеющими меньшее значение в направлении, перпендикулярном стенкам. Кроме того, в (4) необходимо заменить условие прилипания условием Стокса U = b д U д y , где b — безразмерная длина скольжения. Для оценки влияния этих изменений на поведение системы произведём преобразования, аналогичные осуществлённым выше. Уравнение (5) формально остаётся тем же, но другими становятся выражения для локальной напряжённости тангенциального поля и для скоростей U_p и U_e :

U р =^П ( y 2 - a ²) ,

a ² = H ² + 2 bH , U e =k E [ф-Z- b °| •

I 8 J

Как следствие, перестраиваются выражения для расходов:

Q„ =П H ^f H- - a a

^V p      2 I 3

,

Q e =k E

80 о H , 4CH , o) ---i=coth-- bH— , | C Cc      8      8 J

и для тангенциальной напряжённости E :

M =     ⁴ Q ^{8 f o} ( a ² - HЛ + Z H

—

H ( a ² - H ²/3) l 2 8⁽         ) ^S

"1 + 2 Z C ? H + 1 , с J      a x

N =--- ^fC H - ^f + к (g² H + £g_ CH C2) + 2 CH .

H ( a ² - H ²/3 ) l C )    (                  )

Поскольку вязкость и коэффициент диффузии уменьшаются, увеличивается значение коэффициента к . Нахождение точного выражения для его изменения выходит за рамки данной статьи, но по уже приведённым данным можно оценить характер влияния введённых поправок на решение задачи.

• 4.    Результаты моделирования

Для того чтобы лучше понять физику течения электролита в наноканале, рассмотрим канал постоянной ширины H = 1 длиной L . Задача, что очевидно, имеет стационарное однородное по потоку решение с постоянной концентрацией соли C = 1. Коэффициент сцепления и безразмерная длина скольжения неотрицательны, к >  0 , b >  0 . Для определённости положим g <  0 (что соответствует, в частности, случаю течения воды в стеклянном канале) и зададим разность потенциалов А V = E ■ L >  0 и разность давлений А Р = П L >  0 между входом и выходом. Два оставшихся параметра задачи — полурасход Q и ток I , вычислим из следующих соотношений:

• - АР _{и    х} А V f .1 b )

Q = —(1 + 3b) + kg--- £ — ch---;(11)

• 3 L          L Vee)

• — 2g£ ² А Р f    , 1 b f А V Г_       f<1,21 7 fl

I =------- e — ch---+--2 + kg2 1 + £ ch — ch2 — + b .(12)

• L V e ej   L L I e e)_

При таких параметрах оба вклада в расход, напорный и электростатический, положительны. Из второго соотношения, которое по сути является вольт-амперной характеристикой, видно, что ток создаётся как разностью давлений, так и разностью потенциалов, причём зависит от них линейно. Если А Р = 0, то соотношение (12) представляет собой закон Ома, где коэффициент пропорциональности есть электрическая проводимость. Первый член в квадратных скобках, равный 2, — это обычная объёмная проводимость, а второй — поверхностная проводимость. Их отношение называется числом Духина:

„     kg ² f _      . 1    . ₂ 1 , f

Du =--- 1 1 + e ch — ch — + b I .

• 2 V e e )

Как отмечалось выше, такое простое решение справедливо лишь при малых g , но не имеет ограничений по e . Размерная длина скольжения Стокса может достигать 100 нм [18, 19], что при ширине наноканала в диапазоне от 6 до 50 нм соответствует безразмерной длине Стокса b = 2 + 20 . Изменение b на порядок приводит к увеличению в разы как расхода, так и тока. Вклад поверхностного тока, по сравнению с вкладом объёмного, также становится больше. В этом диапазоне ширины наноканала работы [15, 17] предсказывают уменьшение коэффициентов вязкости ц и диффузии D . Обе величины входят в коэффициент сцепления к , который при их уменьшении увеличивается. Следовательно, вырастут значения и параметров Q , I , а также число Духина. Так как экспериментальные данные об изменении b , ц и D весьма противоречивы, получить их количественные зависимости не представляется возможным.

Отдельно рассмотрим случай большого e, возникающий при переходе от малых чисел Дебая к большим, с перекрытием ДЭС. Из (12), (13) можно заключить, что электроосмотический вклад в расход Q уменьшается в разы (и стремится к нулю при e ^ да ), как и вклад давления в создание тока I , то есть задача фактически становится несвязанной. В то же время вклад электроосмотической части в создание тока увеличивается, однако при значениях e >  1 практически не меняется. Аналогично ведёт себя число Духина после достижения значения Du = kg ² ( 2 + 3 b ) /6 .

Случаи с непостоянной шириной канала требуют численного решения асимптотического уравнения (10). В настоящей работе неизвестные функции дискретизировались на равномерной сетке. Производные по пространству задавались разностными схемами второго порядка, для интегрирования по времени использовался полунеявный метод Рунге–Кутты третьего порядка [25]. В качестве неявной части рассматривались якобиан численного оператора и его упрощение, в котором элементы, стоящие вне трёх главных диагоналей, полагались равными нулю. Как показали расчёты, принятое упрощение практически не влияет на устойчивость метода.

Далее приводятся результаты исследования канала двух простых форм: конфузорной (Рис. 2 а ) и диффузорной (Рис. 2 б ). Выбор обусловлен тем фактом, что любой достаточно короткий участок приближении можно считать имеющим клиновидную форму. Следовательно, функция H является однопараметрической: H = 1 + у x/L .

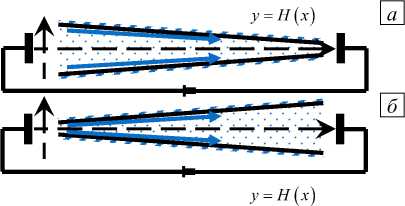
Рис. 2. Конфузорный ( а ) и диффузорный ( б ) клиновидные каналы

начинает нарастать медленнее, по сравнению с

В расчётах брались значения: L = 2000; к = 0.26 (раствор хлористого калия); плотность заряда стенок а = - 0.1 (для простоты задавалась постоянной); безразмерная длина Стокса b = 0 ; расход Q = 0.1; число Дебая е = 0.1; 0.5; 5.0. Таким образом, рассчитывались классический тонкий слой Дебая с толстым электронейтральным слоем, ДЭС с сильно перекрытыми заряженными слоями и промежуточный случай.

Обе конфигурации канала, и конфузорная, и диффузорная, отличаются нелинейностью вольт-амперной характеристики, причём в первом случае ток каналом постоянного сечения, а во втором — быстрее.

Нелинейность наиболее заметна в расширяющемся канале, когда приложенная разность потенциалов А V

положительна (Рис. 3). При увеличении числа Дебая нелинейность усиливается. Для сужающегося канала она выражена не так ярко, однако наблюдается другой эффект: если А V оказывается больше некоторого критического значения А V*, ток резко падает практически до нуля, причём значение А V* уменьшается с ростом е (Рис. 4). Данный результат имеет некоторое сходство с предельным токовым режимом в мембранных системах [1, 2] (ток перестаёт увеличиваться с ростом приложенной разности потенциалов, и график вольт-амперной характеристики приобретает плоский участок), поэтому, следуя терминологии [1, 2], случай при А V < А V* будет называться допредельным, а при АV > А V* — предельным.

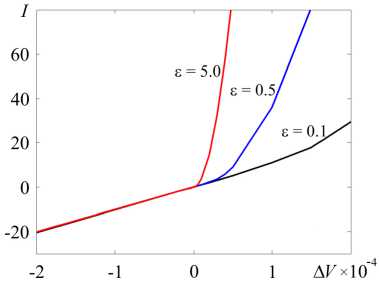
Рис. 3. Асимметрия вольт-амперной характеристики в диффузорном канале, у = + 0.1

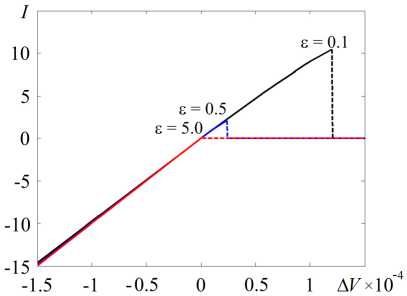
Рис. 4. Асимметрия вольт-амперной характеристики в конфузорном канале, у = - 0.1; пунктиром изображён предельный случай

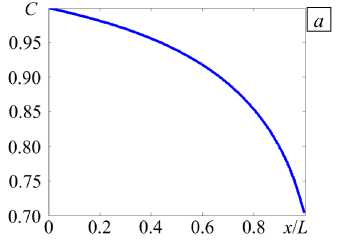
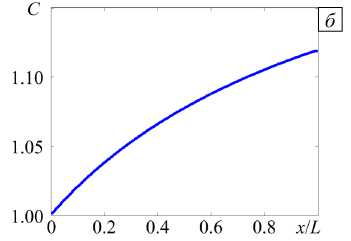
Рис. 5. Распределение концентрации соли при е = 0.1, А V = 4000 вдоль конфузорного, у = - 0.6 ( а ) и конфузорного, у = + 0.6 ( б) каналов

На рисунке 5 представлены стационарные профили концентрации соли в растворе электролита для допредельного случая в конфузорном и диффузорном каналах. Сужение канала приводит к уменьшению концентрации, а расширение — к её увеличению. При этом C ( x ) , в отличие от H ( x ) , не является линейной функцией. Поведение концентрации качественно соответствует приведённому в [20].

В работах [21, 22] в полной постановке найдены нестационарные скачки концентрации, аналогичные ударным волнам газовой динамики, которые получены также в модельных подходах [23, 24]. Уравнение (10) тоже имеет решения типа бегущих волн сжатия или разрежения. Эти скачки играют роль только в начальном нестационарном режиме, после прохождения через всю длину канала они исчезают, и режим становится стационарным. Поэтому такого рода скачки не представляют интереса для данной работы. Гораздо интереснее стационарные скачки, напоминающие висячие скачки в газовой динамике.

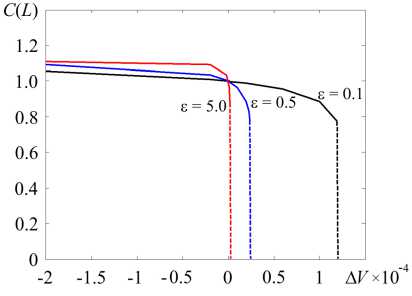
Рис. 6. Зависимость концентрации соли на выходе из конфузорного канала, у = - 0.1, от приложенной разности потенциалов; пунктиром изображён выход на предельный случай

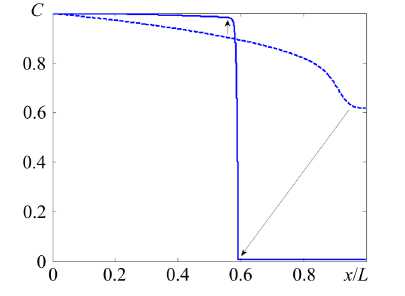
Рис. 7. Динамика профиля концентрации в предельном случае, у = -0.2 , £ = 0.5 , АV = 2000 ; скачок концентрации

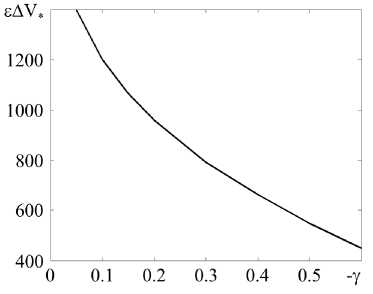
Рис. 8. Зависимость произведения     еА V *

от коэффициента сужения у

При увеличении А V в конфузорном канале уменьшается концентрация соли на выходе — C ( L ) (Рис. 6). При достижении критической разности потенциалов А V = А V * значение C ( L ) в какой-то момент времени начинает резко опускаться до около нулевых значений.

Анализ динамики C ( x ) для предельного случая представлен на рисунке 7. На выходе из канала начинает формироваться плоский (с постоянной концентрацией) участок, который впоследствии расширяется в сторону входа в канал. Концентрация в этой области уменьшается практически до нуля. Напротив, вблизи входа в канал она меняется слабо, за счёт чего в канале образуется характерный скачок.

Качественно аналогичный эффект наблюдался в экспериментах [27] по выпрямлению тока. Несмотря

на различия в геометрии, можно отметить, что вольт-амперная характеристика проходит через нуль разности потенциалов практически линейно, а также присутствует локальный максимум обратного тока. Поскольку в [27] рассматривался аналог диода, имеет смысл назвать значение А V* запирающим напряжением. Оно уменьшается с увеличением модуля у (Рис. 8), причём при достаточно сильном сужении канала зависимость АV* (у) приближается к линейной. Следует отметить, что при изменении с произведение сА V* остаётся практически постоянным.

5.    Заключение

Выше описано упрощённое моделирование течения раствора электролита в наноканалах переменного сечения в рамках континуального подхода. В отличие от аналогичных работ, при упрощении не принимается предположение малости толщины дебаевского слоя. Численно получены установившиеся течения в каналах простейшей геометрии и изучено влияние изменения формы вдоль оси вращения на электрокинетические свойства каналов, в том числе используемые в приложениях [27, 28]. Даны качественные оценки последствий отклонения от континуального подхода.

За рамками работы остались сложные варианты геометрии и свойств канала. При численной реализации используются дискретные значения функций H и а , поэтому их фактические профили могут иметь любую форму, ограниченную только количеством узлов сетки и требованием малости изменений вдоль канала. Логичным продолжением исследований представляется рассмотрение электролита с большим числом ионов, в том числе со взвешенными заряженными частицами. Математически эта задача сводится к добавлению к уравнению (1) аналогичных уравнений с дополнительными коэффициентами в правой части (относительными коэффициентами диффузии и зарядовыми числами). И тогда вместо уравнения (10) будет решаться система аналогичных по структуре уравнений, а численный алгоритм принципиально будет тем же. Дополнительная асимметрия, связанная с различием зарядовых чисел или коэффициентов диффузии, может быть причиной эффектов концентрирования, наблюдавшихся в [11, 12].

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-29-00307),