Влияние эффективной проницаемости среды на устойчивость двухслойной системы «однородная жидкость - пористая среда» в поле вибраций высокой частоты

Изучается влияние высокочастотных вертикальных вибраций и эффективной проницаемости пористой среды на возбуждение конвекции в подогреваемой снизу двухслойной системе, состоящей из слоя однородной жидкости и расположенного под ним слоя пористой среды, насыщенной той же жидкостью, в поле силы тяжести.

Возникновение конвекции в двухслойной системе «пористая среда – одно- или двухкомпонентная жидкость» в статическом поле силы тяжести исследовалось в работах [1–4]. Бимодальный характер нейтральных кривых для системы горизонтальных слоев однородной жидкости и пористой среды, насыщенной жидкостью, впервые описан в работе [1]. Рассматривалась трехслойная система, состоящая из слоя жидкости, окруженного двумя пористыми слоями. Уравнения конвекции в жидком и пористом слоях записывались в приближении Дарси–Буссинеска с применением граничного условия равенства нулю касательной компоненты скорости жидкости на границе раздела двух сред. Показано, что при достаточно больших толщинах жидкого слоя и малых проницаемостях пористой среды наиболее опасными становятся коротковолновые возмущения, локализованные в основном в жидком слое. В [2] для описания конвекции в двухслойной системе «однородная жидкость – пористая среда, насыщенная жидкостью» использовалась модель Бринкмана–Буссинеска, учитывающая помимо силы сопротивления пористого скелета движению жидкости в среде, которая рассматривается в рамках модели Дарси–Буссинеска, вязкую диффузию жидкости в пористой среде. Нейтральные кривые монотонной неустойчивости, полученные в рамках этой модели и в рамках модели Дарси–Буссинеска, качественно согласуются.

В работах [3, 4] рассматривалось влияние отношения толщин жидкого и пористого слоев на возбуждение конвекции в двухслойной системе «одно- или двухкомпонентная жидкость – пористая среда, насыщенная жидкостью» в статическом поле силы тяжести. В [3] использовались различные уравнения для описания конвекции в пористом и жидком слоях, а в [4] конвективное течение исследовалось с помощью единого уравнения для двух сред, но путем введения неоднородной пористости m , которая на твердой

границе имела значение, равное 0, в пористой среде — от 0 до 1 и в жидкости — 1. Показано, что в случае тепловой конвекции увеличение толщины жидкого слоя приводит к понижению порога устойчивости механического равновесия системы. Полученные в [3, 4] результаты качественно согласуются.

Роль высокочастотных вибраций в возбуждении конвекции в горизонтальном слое пористой среды, насыщенной однокомпонентной жидкостью, изучалась в работах [5–7]. Установлено, что вертикальные вибрации повышают устойчивость системы вплоть до полной стабилизации равновесия. Основной эффект воздействия высокочастотных поступательных вибраций на неоднородные среды описан в [8] и заключается в появлении средней силы, влияющей на неоднородности плотности. В случае, когда направления градиента температуры и оси вибраций совпадают с направлением силы тяжести, действие средней вибрационной силы приводит к стабилизации механического равновесия жидкости. Становится устойчивым равновесие как однородной жидкости, так и пористой среды, насыщенной однородной жидкостью. Приход в устойчивое состояние наблюдается и в двухслойной системе (см. работы [9, 10], где исследовалась устойчивость механического равновесия в двухслойной системе, состоящей из горизонтальных слоев однокомпонентной жидкости и пористой среды, насыщенной жидкостью, в поле силы тяжести и высокочастотных вибраций). В [9] рассмотрен случай тонкого жидкого слоя. Найдены эффективные граничные условия на верхней границе пористого слоя, учитывающие влияние конвекции в жидкой прослойке, и получено, что вибрации повышают порог устойчивости, а жидкая прослойка играет дестабилизирующую роль. Длина волны наиболее опасных возмущений растет с увеличением интенсивности вибраций и утолщением жидкой прослойки. В [10] рассмотрен более общий случай произвольной толщины жидкого слоя и показано, что вибрации, ввиду малости инерционных эффектов в пористой среде по сравнению с жидким слоем, оказывают более сильное влияние на коротковолновые возмущения, в основном локализованные в жидком слое, чем на «длинноволновые», охватывающие оба слоя в целом (здесь и ниже под длинноволновыми возмущениями понимаются возмущения, соответствующие минимуму нейтральной кривой при меньшем волновом числе).

Роль высокочастотных вибраций в возбуждении конвекции в двухслойной системе «однородная жидкость – пористая среда, насыщенная той же жидкостью» при изменении эффективной проницаемости пористой среды не изучалась.

• 2.    Постановка задачи. Определяющие уравнения и граничные условия

Рассмотрим задачу устойчивости механического равновесия в двухслойной системе, состоящей из слоя однородной жидкости и расположенного под ним слоя пористой среды, насыщенной той же жидкостью, в поле силы тяжести. Система ограничена сверху и снизу твердыми изотермическими границами и подвергается вертикальным гармоническим вибрациям с амплитудой a и частотой ω .

Уравнения свободной тепловой конвекции в жидком слое записываются в приближении Буссинеска, в пористом слое — в приближении Дарси–Буссинеска [11]. Задача имеет решение, соответствующее механическому равновесию, при котором распределение температуры в слоях однородной жидкости T0 (z) и пористой среды ϑ0 (z) является линейным: ∇T0 =-Af , ∇ϑ0 = -Am, где Af, Am — вертикальные градиенты температуры в жидкости и пористой среде в состоянии механического равновесия.

Уравнения, описывающие малые возмущения равновесия, в системе отсчета, связанной с колеблющимися границами слоя, имеют вид в жидком слое:

∂ ^v =- ¹ ∇ p + ν ∆ v + g β T γ - a ω²β T γ cosω t ,                           (1)

∂t     ρ f в пористом слое:

∂ T = χ f ∆ T + Af v ⋅ γ, ∂ t	div v = 0;	(2)
1 ∂ u      1ν =- ∇ pm - u + g β ϑ γ m ∂ t    ρ      K	- a ω2β ϑ γ cosω t ,	(3)
b ∂ϑ = χ eff ∆ϑ+ Am uγ ⋅ , ∂ t	div u = 0 .	(4)

Здесь v — скорость конвективного движения в чистой жидкости; u — скорость конвективной фильтрации в пористой среде, насыщенной жидкостью; p_f , p_m — давления в жидкости и пористой среде без учета гидростатической добавки; T , ϑ — отклонения температуры в жидкости и пористой среде от средних значений; ρ — плотность жидкости, ν — кинематическая вязкость жидкости; g — ускорение силы тяжести; β — коэффициент объемного расширения жидкости; m — коэффициент пористости;

K — коэффициент проницаемости среды; b — отношение теплоемкостей единиц объема пористой среды и жидкости; χ _f ,χ _m — температуропроводности жидкости и пористой среды; χ _eff — эффективная температуропроводность, связанная с температуропроводностью пористой среды соотношением X f = b X _m ; Y — орт вертикальной оси.

На твердой поверхности, ограничивающей двухслойную систему снизу, исчезают нормальная компонента возмущений скорости и возмущения температуры, на верхней границе — возмущения скорости и температуры:

z = - h m : u ■ y = 0, 9 = 0,

z = h f : v = 0, T = 0 .

Здесь h_m , h_f — толщины жидкого и пористого слоев соответственно.

На границе раздела слоев выполняются условия непрерывности температуры и теплового потока:

z = 0: T = 9 ,

d T

^K f Z ^K m d z

d9 d z

В качестве гидродинамических граничных непрерывность нормальной компоненты скорости, касательной компоненты скорости жидкости [1]:

условий на поверхности раздела принимаются: непрерывность давления и условие равенства нулю

z = 0: v ■ Y = u ■ Y ,     Pf = P m , v T = 0.

Поясним последнее граничное условие. Поскольку при движении в пористой среде жидкость испытывает сопротивление пористого скелета, скорость конвективной фильтрации в пористом слое, как правило, мала по сравнению со скоростью жидкости в жидком слое. Это дает основание предположить, что тангенциальная компонента скорости жидкости при переходе через границу раздела двух сред меняется скачком, и для жидкого слоя ее можно положить равной нулю на границе раздела.

Ограничимся рассмотрением вибраций с малой по сравнению с характерным размером задачи амплитудой a <<  h m . Частота вибраций предполагается настолько большой, что толщина вязких пограничных слоев вблизи твердых границ слоя и границы раздела δ мала по сравнению с характерным размером задачи h _m : ю h m¹ /v >>  1, ^v/ю = 5 <<  h m . В этом случае все поля можно представить в виде сумм средних и пульсационных компонент и, применив метод осреднения, получить уравнения для этих компонент. Уравнения тепловой вибрационной конвекции в однородной жидкости можно найти в [12]. Вывод уравнений тепловой вибрационной конвекции в пористой среде, насыщенной жидкостью, осуществлен в [5].

Отметим, что введенные приближения справедливы в диапазоне частот от вязких до звуковых, поскольку среда считается несжимаемой, то есть при v/ h m 2 <<  ю <<  с/h m . Здесь с — скорость звука. Например, для воды (v = 0,01см²/с) при h_m = 1 см диапазон допустимых частот составляет: 10 ^{- 2} <<  ю <<  10 5 с^-1.

В работах [9, 10] подробно описан вывод уравнений вибрационной конвекции в двухслойной системе «однородная жидкость – пористая среда, насыщенная той же жидкостью» в поле силы тяжести и высокочастотных вибраций. Поэтому далее приведем уравнения вибрационной конвекции для осредненных по периоду вибраций полей скорости, температуры и давления только в окончательной безразмерной форме: в жидком слое:

— dv =-1 vp + Av + R^-Tч +кbR y Re( iVy ),(9)

Prm d t     e              ee dT _ о

X— = AT + к2 vy , div v = 0,(10)

dt iQV = -VPf -Ty ,   div V = 0 ;(11)

в пористом слое:

е du D . = Vpm u +Rp 9Y +rpvRe( 1W ■ Y) Y , m Prm dt (12) d9 . „ — = A9 + u ■ Y , div u = 0, dt (13) z'QW ----= -VPm - W -9y , div W = 0 m (14) с граничными условиями

z = 0 : vy = uy ,   vT = 0, T = 9 ,	ат d9 = к , pf = p m , V ■ Y = W ■ Y ,    P f = P m ,    (15) az    az
z = d : v = 0,	T = 0, V ■ Y = 0,
z = - 1: u ■ у = 0,	9 = 0, W ■ y = 0.                                   (16)

Здесь v_T — касательная компонента скорости жидкости; к = к m /к f , где к f ,к m — теплопроводности жидкости и пористой среды; V , W , P_f , P_m — комплексные амплитуды пульсационных полей скорости и давления в однородной жидкости и пористой среде.

В качестве единиц измерения величин выбраны следующие: [T] = [9] = 9 = AmL ; [v] = [u] = Xeff I(LAm ) ; [V ] = [ W ] = a И^О K/V ;    [ Pf ]=[ Pm ] = a Ю2Р0 Le ;    [ t ]= bL2 /xeff ;    [ pf ] = [ Pm ] = ПХ eff 9/(LKAm ) , где характерный масштаб L равняется толщине пористого слоя hm .

Задача (9)-(16) содержит следующие безразмерные параметры: число Прандтля Pr m = v/x _m и число Релея R p = g в KL A m IV VX eff ) для пористой среды; вибрационное число Релея R _{p v} = ( а и A m в KL ) 2 и/(2 bv ² х eff ) для пористой среды; безразмерную частоту вибраций Q = и K /v ; безразмерную толщину жидкого слоя d = hf/h m , параметр Дарси е = K] L 2 ; отношение теплопроводностей пористой среды, насыщенной жидкостью, и жидкости κ ; отношение температуропроводностей пористой среды, насыщенной жидкостью, и жидкости х = к/ b = X _m /X _f • Здесь b = (р C_p )_тДр C_p )_у , где C_pf , C_pm — удельные теплоемкости при постоянном давлении в жидкости и в пористой среде.

Ограничимся исследованием монотонной неустойчивости. Исключая давление и горизонтальные компоненты скоростей и рассматривая периодические вдоль оси x возмущения (все поля пропорциональны cos( kx ) , где k — волновое число возмущений), получаем спектральную задачу для нейтральных возмущений в жидком слое:

eA2v + RpA2T + кbRpvА2 Re(iV) = 0 ,(17)

AT + к2 v = 0,(18)

iQA V = -A2T ;(19)

в пористом слое:

Au - RpA29- RpvA2Re(iW) = 0,(20)

A9 + u = 0,(21)

iQ AW =-A W -A29

m с граничными условиями:

„         dv Л d3 v  du A n   dT d9             d V f 1    1 )d W z = 0: v = u, — = 0,  е—r +--= 0,  T = 9,  — = к —,  V = W,  —=--i— ---,(23)

dz        dz3 dz               dz    dz              dz (m   Q J 5z z = d : v = o, — = o, T = о, V = o, dz

z = - 1: u = 0,    9 = 0, W = 0.

d ²

Здесь v , u , V , W — вертикальные компоненты векторов v , u , V , W ; A = ——- k , A d z²

d ⁴

d z⁴

—

2 k2     + k4, dz2

A ₂ =- k².

Для системы уравнений (17)–(22) с граничными условиями (23), (24) численно строилась фундаментальная система решений с учетом ортогонализации базисных векторов частных решений [13, 14]. Полученная система однородных дифференциальных уравнений для векторов частных решений, удовлетворяющих условиям на верхней и нижней твердых границах двухслойной системы (24), решалась в каждом из слоев методом Рунге-Кутты–Мерсона пятого порядка с автоматическим выбором шага интегрирования. В некоторых точках интервала интегрирования применялся метод ортогонализации по Граму–Шмидту [15]. Из стыковки векторов частных решений на границе раздела слоев (условия (23)), получалась задача на собственные значения, из решения которой находились параметры задачи.

• 3.    Результаты численного исследования

  

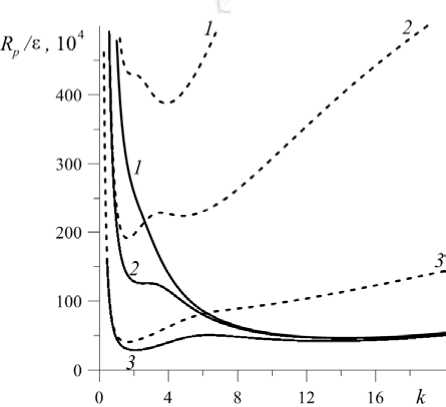
  Рис. 1. Нейтральные кривые устойчивости равновесия при d = 0,20 и различных значениях эффективной проницаемости пористой среды £, 10 ^{— 6}: 4 (кривая 1 ), 10 ( 2 ), 50 ( 3 ), для двух значений вибрационного числа Релея R pv = 0 (сплошные линии) и R pv = 50 (штриховые линии)

  
  

Численное исследование устойчивости механического равновесия двухслойной системы «однородная жидкость – пористая среда, насыщенная той же жидкостью» в поле силы тяжести и высокочастотных вибраций проводилось при фиксированных значениях следующих параметров: Q = 1, b = 1, к = 1,43, m = 0,25 . Рассматривалось влияние изменения безразмерной толщины жидкого слоя, эффективной  проницаемости пористой среды и вибрационного числа Рэлея в пористой среде на устойчивость равновесия системы.

На рисунке 1 изображено семейство нейтральных кривых при d = 0,20 и различных значениях эффективной проницаемости пористой среды б для двух значений вибрационного числа Рэлея: Rpv = 0 и Rpv = 50. Видно, что в области малых значений б , как при наличии вибраций, так и в их отсутствие, наиболее опасными являются коротковолновые возмущения (то есть возмущения с большим значением волнового числа k ), локализованные в основном в жидком слое (кривые 1). Поскольку при движении в пористой среде жидкость испытывает сопротивление пористого скелета, при малых значениях проницаемости гидродинамические возмущения практически не проникают в пористую среду, а сосредоточены главным образом в слое жидкости. С ростом эффективной проницаемости пористой среды наиболее опасными становятся длинноволновые возмущения (то есть возмущения с малым значением волнового числа k ), охватывающие и слой жидкости, и слой пористой среды (кривые 3). При дальнейшем увеличении эффективной проницаемости пористой среды коротковолновый минимум полностью исчезает. Полученные результаты качественно согласуется с результатами работы [1], где решалась линейная задача возбуждения конвекции в трехслойной системе, состоящей из подогреваемого снизу слоя однокомпонентной жидкости, который располагается между двумя пористыми слоями, насыщенными той же жидкостью. Вибрации приводят к повышению порога устойчивости равновесия и росту длины волны наиболее опасных возмущений (см. штриховые кривые 1–3, Рис. 1).

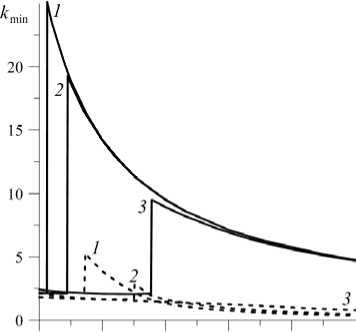
На рисунке 2 представлены зависимости волнового числа наиболее опасных возмущений от безразмерной толщины жидкого слоя при различных значениях эффективной проницаемости пористой среды для двух значений вибрационного числа Рэлея: Rpv = 0 и Rpv = 50 . Легко видеть, что с ростом толщины жидкого слоя происходит скачкообразный переход от длинноволновых возмущений к коротковолновым (кривые 1, 2 и сплошная кривая 3). Влияние вибраций на коротковолновые возмущения оказывается гораздо сильнее, чем на длинноволновые. Такое различие связано с тем, что коротковолновые возмущения локализованы в основном в жидком слое, а длинноволновые охватывают всю систему. Инерционные эффекты, ввиду малости параметра ε , в пористом слое выражены слабее, чем в однородной жидкости, поэтому влияние вибраций на длинноволновые возмущения слабее, чем на возмущения, локализованные в жидком слое. Этот результат согласуется с результатом, представленным в работе [10]. С ростом проницаемости пористой среды длина волны наиболее опасных возмущений растет (см. кривые 1–3, Рис. 2).

Рисунок 3 содержит зависимости волнового числа наиболее опасных возмущений от эффективной проницаемости пористой среды при различных фиксированных значениях безразмерной толщины жидкого слоя для двух значений вибрационного числа Рэлея: R pv = 0 и R pv = 50. Как было отмечено ранее, при малых значениях ε равновесие является неустойчивым по отношению к коротковолновым возмущениям, локализованным в жидком слое (см. кривые 1 , Рис. 1). С ростом ε гидродинамические возмущения начинают проникать в пористую среду, и при некотором значении этого параметра (например, для d = 0,20 и R pv = 0 — это е = 3,22 - 10 ^{- 5}) происходит переход от коротковолновой к длинноволновой неустойчивости (см. кривые 1 , 2 на Рис. 3). Вибрации приводят к тому, что длинноволновая неустойчивость равновесия в системе возникает при меньших проницаемостях пористой среды и больших безразмерных толщинах жидкого слоя, чем в случае статического поля силы тяжести (см. например, кривые 1 на Рис. 2 или кривые 2 на Рис. 3).

0,1 0,2 0,3 0,4 0,5 d

Рис. 2. Зависимости волнового числа наиболее опасных возмущений равновесия от безразмерной толщины жидкого слоя при различных значениях эффективной проницаемости пористой среды е, 10 ^{- 6}: 4 (кривая 1), 10 ( 2 ), 100 ( 3 ) для двух значений вибрационного числа Релея R pv = 0 (сплошные линии) и R pv = 50 (штриховые линии)

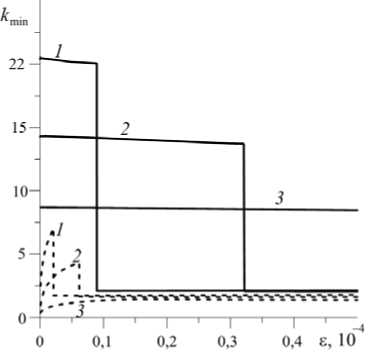
Рис. 3. Зависимости волнового числа наиболее опасных возмущений равновесия от эффективной проницаемости пористой среды при различных значениях безразмерной толщины жидкого слоя d : 0,14 (кривая 1 ), 0,20 ( 2 ), 0,33 ( 3 )

для двух значений вибрационного числа Релея R p_v = 0

(сплошные линии) и R p_v = 50 (штриховые линии)

Далее приводятся карты устойчивости для наиболее опасных возмущений в зависимости от безразмерной толщины жидкого слоя при различных значениях эффективной проницаемости пористой среды (Рис. 4) и безразмерной толщины жидкого слоя (Рис. 5). Сплошными линиями показаны кривые в отсутствие вибраций, штриховыми линиями — кривые при R pv = 50 . Как видно из рисунков, вибрации стабилизируют равновесие системы во всем исследуемом диапазоне параметров. Изломы кривых при увеличении безразмерной толщины жидкого слоя и уменьшении проницаемости среды связаны с переходом от наиболее опасных длинноволновых возмущений к наиболее опасным коротковолновым. Кривые 1 – 3 на рисунках 4 и 5 свидетельствуют о том, что увеличение толщины жидкого слоя и проницаемости среды приводит к понижению устойчивости равновесия системы.

На рисунке 6 представлена диаграмма на плоскости параметров е - h (где h = У d ), где кривыми 1 и 3 ограничена область существования нейтральных кривых с двумя минимумами: коротковолновым и длинноволновым. При параметрах из области между кривыми 1 и 2 длинноволновые минимумы оказываются ниже коротковолновых, а при параметрах из области между кривыми 2 и 3 (заштрихованная область) наиболее опасны коротковолновые минимумы. Выше кривой 1 находится область параметров, при которых нейтральные кривые имеют один длинноволновый минимум. Область параметров, лежащая ниже кривой 3 , соответствует нейтральным кривым с одним коротковолновым минимумом. В точке, где все три кривые сходятся (пик области), параметры имеют значения: е = 8,12 - 10^-4 и h = 1,89 ( d = 0,53).

Заметим, что при любых значениях эффективной проницаемости пористой среды для достаточно больших толщин жидкого слоя (при d >  0,53) возмущения практически не проникают в пористую среду и охватывают только слой жидкости.

На рисунке 7 изображены две диаграммы на плоскости параметров е - h при R pv = 0 и R pv = 50. На диаграммах кривыми 1 и 3 ограничена область существования двух минимумов: коротковолнового и длинноволнового. В заштрихованных областях более опасными являются коротковолновые минимумы. Как видно, вибрации приводят к сужению интервала значений параметров ε и h , в котором нейтральные кривые являются бимодальными. Таким образом, в поле высокочастотных вибраций уже при малых значениях проницаемости пористой среды и достаточно больших толщинах жидкой прослойки длинноволновые возмущения становятся наиболее опасными и, как видно из рисунка, заштрихованная область сдвигается в сторону меньших значений ε и больших значений d . В отличие от безвибрационного случая, при котором максимальное значение эффективной проницаемости пористой среды ε , характерное для нейтральных кривых с двумя минимумами, резко уменьшается с ростом h , при наличии вибраций существует некоторое максимальное критическое значение параметра ( h ® 7,7), ниже которого наблюдается умеренный рост эффективной проницаемости среды.

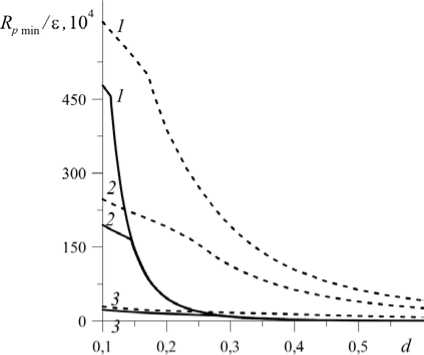
Рис. 4. Карты устойчивости для наиболее опасных возмущений в зависимости от безразмерной толщины жидкого слоя при различных значениях эффективной проницаемости среды е, 10 - 6 : 4 (кривая 1 ), 10 ( 2 ), 100 ( 3 ) для двух значений вибрационного числа Релея R pv = 0

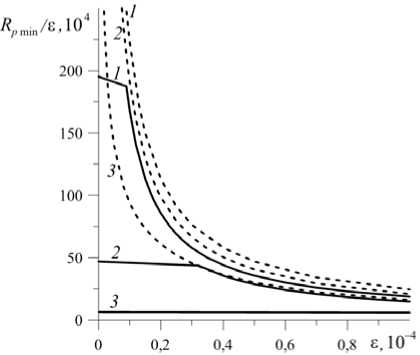
Рис. 5. Карты устойчивости для наиболее опасных возмущений в зависимости от эффективной проницаемости среды при различных значениях безразмерной толщины жидкого слоя d : 0,14 (кривая 1 ), 0,20 ( 2 ), 0,33 ( 3 ) для двух значений вибрационного числа Релея R pv = 0 (сплошные

(сплошные линии) и R pv = 50 (штриховые линии)

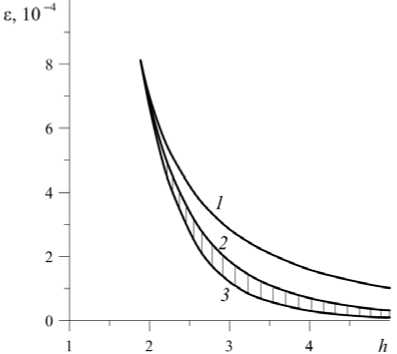
Рис. 6. Диаграмма е - h ; кривые 1 и 3 ограничивают область существования двух минимумов (заштрихована та ее часть, где наиболее опасными являются коротковолновые возмущения)

линии) и R pv = 50 (штриховые линии)

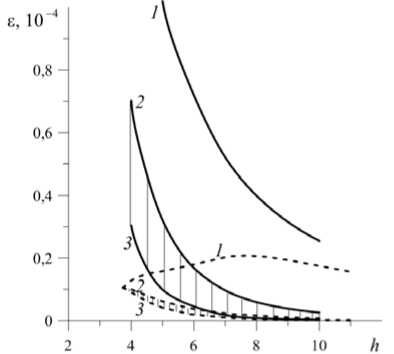
Рис. 7. Области существования двух минимумов нейтральных кривых при R pv = 0 (сплошные линии)

и R pv = 50 (штриховые линии)

• 4.    Заключение

В работе исследовано влияние величины эффективной проницаемости среды на возникновение конвекции в подогреваемой снизу двухслойной системе «однородная жидкость – пористая среда, насыщенная той же жидкостью» в поле силы тяжести в отсутствие и при наличии высокочастотных вибраций.

Как показали расчеты, в безвибрационном случае с ростом эффективной проницаемости пористой среды и с уменьшением толщины жидкого слоя длина волны наиболее опасных возмущений растет. Это связано с тем, что при движении в пористой среде жидкость испытывает сопротивление пористого скелета, и, соответственно, чем выше проницаемость среды и меньше влияние жидкого слоя, тем легче возмущения проникают в слой пористой среды, приводя к развитию длинноволновой неустойчивости.

При наличии вибраций нейтральные кривые, как и в случае статического поля силы тяжести, в некотором диапазоне параметров являются бимодальными. Получены диаграммы существования нейтральных кривых с двумя минимумами. Показано, что в поле высокочастотных вибраций длинноволновые возмущения становятся наиболее опасными при меньших значениях проницаемости пористой среды и больших толщинах жидкого слоя, чем в отсутствие вибраций, когда при малых значениях проницаемости среды и умеренных толщинах жидкого слоя неустойчивость равновесия в системе связана с развитием коротковолновых возмущений.