Влияние кинематических параметров процесса алмазной резки заготовок из полимерного композиционного материала на значение плотности теплового потока

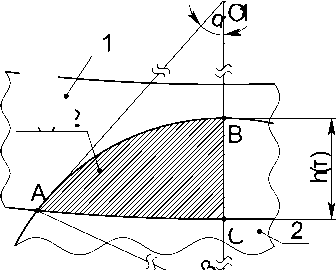
Значения плотности теплового потока q c на разных участках режущей кромки при разрезании алмазными отрезными кругами определяя-ются кинематическими параметрами процесса и температурой по длине дуги контакта режущей кромки с заготовкой из полимерных композиционных материалов (ПКМ) [1]. Определим площадь и длину дуги контакта во время разрезания заготовки. Рассмотрим изменение длины дуги контакта на различных стадиях процесса разрезания цилиндрической заготовки (рис. 1). В дальнейшем обозначено: R н =150 мм – наружный радиус круга; r внут .=140 мм – внутренний радиус режущей кромки; R н – r внут = 10 мм; B =25 мм – ширина заготовки; H =25 мм – высота заготовки; τ – время работы, мин.; S верт . – вертикальная подача, м/мин.; l конт .(τ) – длина дуги контакта, м; S (τ) – площадь контакта, м².

1. Врезание . τ<τ max1

^lO 1 A = R H ; ^lO 2 A = r ; ^lO 1 O 2 = R H + r  h ^{( t} )’

h ( J maxi )   s верт ^T maxi    ^RH

r : t внут . ; max 1

= (RH

—

' внут * )/ s верт * *

— R2-

S сект.O , AC     ^ ^Rh ; S сект.O 2 AB

1 конт* ( Т ) = 2l AC = 2 a R H *

P 2 = —r *

2 ^з (1)

Из треугольника O 2 AO 1 по теореме косинусов имеем:

C

S(τ)/ 2

^lO₂A   OA + ^lO 1 O₂   ^2lO 1 A l O) cos ^a ;

a = arccos ^{(( l} OA + l OO^ - l OA )/⁽ 2 l OA l OO, )) =

= ar^{ccos [(} R H ^{+ (} R H ^{+ r} 3 - h ^{( t )) 2} - ^r 2 }/(2 ^R h ⁽ R H ^{+ r} 3 - h ^{( t )))} 1

^lO 1 A   ^lO₂A ^{+ l}O₁O₂   ^2lO₂A^lO₁O₂ ^cos P ;*

^в = ^arccOS [^{( l}O ₂ A ⁺ l OO ₂ - ^lO , A )/⁽ 2 ^lO ₂ A l OO ₂ ^)] =

= arc^{cos [ ( r}3 ^{2 + ( R} h ⁺ r₃ - h ( T ^{)) 2} - R H )/ ⁽ 2 r₃ ^{( R} h ⁺ r₃ - h ( T ^J

^S A O , AO ₂ = 0,^{5 l} O ₁ A l O j O 2 sin ^a             (5)

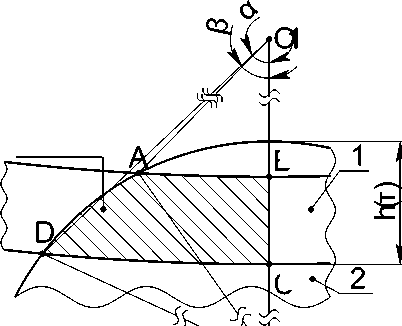
2. Нормальное резание (см. рис.2). τ max1 <τ<τ max2

O2

Рис. 1. К расчётному случаю 1: 1 – режущая кромка АОК («тело» круга условно не показано), 2 – заготовка

L ^r • L =R • L =L =r- ¹O 1 A ' внут * ;    ⁽O 1 D       h ;    ⁽O ₂ A O ) ₂ D ' з ;

¹o 1 o ₂ = ^Rh ^{+ r} 3 - h ^{( t} );

h ^{( t} max2 )   ^$ верт ^Ттах2   ² r 3 ;   ^T max2    ² r 31^S верт *

S(τ)/ 2

B

C

O2

Рис. 2. К расчётному случаю 2. 1 – режущая кромка АОК («тело» круга условно не показано), 2 – заготовка

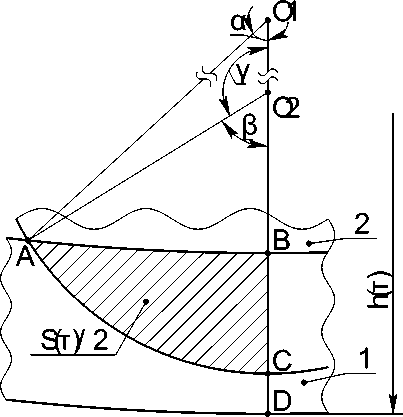
Рис. 3. К расчётному случаю 3. 1 – режущая кромка АОК («тело» круга условно не показано), 2 – заготовка

s ( г ) = 2 ( s„o , dc

—

сект . O ₁ AB

1. н.т Т ) = 2^ = 2 PR_H .

^P /?²-

S сект . О , DC     ^ ^Rh ;    S сект . О , AB

а

= —r . внут . .

Из треугольника О 2 DO 1 по теореме косинусов имеем:

l O₂D  Р D + ^lO₁ O₂  ^2l0_YD l OO cos ^p

^P = arccOs J^ OD + l OO ₂ - l o 2 D )/( ² l O D^lO , о 2 ^)] =

= arccosK R H + ⁽ R_H + r - h I - ^{)) 2 -} г У( ² R_H ^{( R} _H + r , ^- h I - m^]

Из треугольника О 2 АО 1 по теореме косинусов имеем:

^l0 ₂ A   ^lO₁ A ^{+ l}0_Y O₂   ^2lO₁ A^lO₁ O₂ cos ^a ;

a = ^arccos [^ a ⁺ lo,o₂ - lO₂A )/( ^{2 1}o,a¹oo, ^)] =

= arccos K r ^. ^{+ ( R}H ⁺ r , - h C ^{)) 2} - C )/( ² ' внут . ^{( R}H ⁺ r , - ^{h ( t} )) ) ]

3. Окончание реза ния (см. рис. 3). τ max2 <τ<τ max3

I =1 =r - I =R •    /   = /   = r •

¹O , A    0 3 , B     ' внут . ;    0 3 , D    ^H ;      0 2 ₂ A    0 2 ₂ C     r , ;

l0,0₂ = R H ⁺ r , - h ^T ) ; h ^{( t} max 3 ) = s верт . ^T max 3 =

= ² r , ^{+ R} H - ' внут . ;

^T mx3 = ^{( 2} r₃ ^{+ R} H - ' внут . V ^S верт . .

^{S ( t} )   ^{2 (} S ceKrn . О ₂ AC ^{+ S} A O , AO ₂

S сект . O ₁ AB

¹конт . ^{( T} ) = ²¹ AC = ^{2 P} r , .

Из треугольника О 1 АО 2 по теореме косинусов имеем:

^lO₂A   ^lO₁ A ^{+ l}O₁O₂   ^2lO₁ A^lO₁O 2 ^{cos a} ;

a = arccos [(lO^ + lOO2 — lO2A )/(2IoaIoo2 )] =

= arcCOs[(r624m. +(Rh + Гз - h lT ))2 - r2 )/(2 r«„ymkRH + r, - h (T)))} (12)

22  2

l 0 ₂ A = l O-0О ₂ ⁺ l O ₂ A - ^{2 l}O ₂ О ₂ l O ₂ A ^{cos Y} ;

У = ^{arccos [( l}o_iО ₂ ⁺ l o ₂ a ^— lo A )/ ² l o , о ₂ l o ₂ a ^] =

= arcrosK ¹ R H ⁺ r , ^- h ^{( t} )) ^{2 + r}, ^- Г _в Нут .)/ ^{( 2 ( R}H ⁺ r , - h ^{( t} )) r , ^)] (13)

Y + в = n;

P = ^{n -} Y .                 (14)

Выводы: мы получили математические выражения для расчета длин дуги и площади контакта на различных стадиях процесса при разрезании цилиндрической заготовки из ПКМ алмазным кругом.