Влияние конечной проводимости стенок на структуру поля и характеристики круглого волновода

Распространение электромагнитных волн в равновесных системах обязательно сопровождается диссипацией энергии. Тепловые потери являются важной характеристикой волновых процессов, во многом определяющей технические параметры разнообразных приборов и устройств СВЧ- и КВЧ-диапазонов. Поэтому расчету потерь при анализе электромагнитных полей в электродинамических системах уделяется достаточно большое внимание [1–11]. При этом оказывается, что учет потерь приводит не только к количественным изменениям характеристик системы, но в ряде случаев и к качественному изменению структуры полей [7].

Решение уравнений Максвелла для адекватных реальным устройствам моделей представляет весьма трудную задачу. Один из эффективных методов упрощения этой задачи – метод эквивалентных граничных условий, позволяющий исключить из рассмотрения некоторую область пространства (и поле в ней), задавая соответствующие условия на ее границе [1]. Классическим примером являются импедансные граничные условия Щукина – Леонтовича, описывающие поглощение энергии электромагнитного поля в хорошо проводящих средах.

Это условие выводится для плоской безграничной металлической поверхности. Но оно применимо и для криволинейной поверхности, если радиус кривизны много больше характерного масштаба изменения поля (в этом случае граница ведет себя как локально плоская). В произвольном случае можно получить более общие граничные условия, содержащие поправки на кривизну поверхности [2–3] и учитывающие особенности на углах и ребрах [4].

Основная сложность состоит в получении точного выражения для поверхностного импеданса, учитывающего не только параметры материала, но и структуру электромагнитного поля в волноводе. В большинстве работ [5–8] используется приближенное («классическое») выражение для импеданса проводящей поверхности [9], которое обеспечивает точное выполнение граничных условий лишь при нормальном падении волны на поверхность металла.

Строгий расчет с учетом проникновения поля вглубь стенки является примером решения задачи о распространении цилиндрических волн в поперечно-неоднородной среде. Даже в кусочнооднородной по своим свойствам среде в волне, вообще говоря, отличны от нуля все шесть компонент поля и деление волн на магнитные и электрические уже не имеет смысла. Краевая задача для потенциальных функций становится очень громоздкой. Однако для металлов в сантиметровом диапазоне волн волновое сопротивление Z очень малая по модулю комплексная величина, скин-эффект сильно выражен и конечная проводимость с хорошей точностью может быть учтена с помощью граничного условия Щукина – Леонтовича. При этом поле в стенках волновода не представляет интереса, а поле внутри волновода определяется решением тех же уравнений, что и при идеальной проводимости стенок.

Рассмотрим круглый экранированный волновод без диэлектрического заполнения ( б = 1, ц = 1, ст = 0). Считаем, что толщина проводящей

стенки волновода много больше глубины проникновения поля. Запишем уравнения Гельмгольца

относительно продольных составляющих полей

гибридных волн в цилиндрической системе координат:

d 2 Ez	1 5 Ez     1 5 2 Ez	22 d E to
dp 2	+-- z +-- z p dp   p 2 d9 2	+ z + 2 E = °’ 5 z 2     c 2	(1)

d 2 Hz	1 5 H  1 5 2 H	22 d H^ to
dp 2	+-- z +-- z p dp p2 d92	+ z + 2 H = 0. 5 z 2     c 2	(2)

где n — нормаль к поверхности однородной среды с потерями (направлена вглубь среды).

В рассматриваемой нами задаче вектор нормали T n tt e p . В этом случае векторное условие (8) распадается на два условия, связывающие тангенциальные составляющие векторов E и H поля в непроводящей среде на границе с проводником, имеющим волновое сопротивление Z ₂:

Решения этих уравнений имеют вид:

E z ( р , 9 , z ) = AJ n ( xp ) cos n 6 e - j ³ z ,              (3)

H z ( p , 9 , z ) = BJ n ( xp ) sin n 9 e ^- j ^{3 z} ,               (4)

E z =- Z 2 H 9 , E 9 = Z 2 H z , (9)

где

7 - I ^ 0 _г            ^j ^ 2

^Z 2 = J -    , ^Б к2 = ^Б 2         ;

V ^Б 0 ^Бк 2                   ^toE 0

где x = ( to/ c ) - p , x — поперечное волновое число; в — постоянная распространения; A и B — произвольные постоянные; n = 0, 1, 2, ...; c —

скорость света в вакууме.

Составляющие полей E p , E 9 , H р и H 9 определяются из соотношений:

Б _к 2 — относительная комплексная диэлектрическая проницаемость проводящей среды; ^ 2 — проводимость.

Применяя граничное условие (9) к выражениям для компонент поля (7) получим систему уравнений относительно постоянных A и B :

F - - j I ⁵ Ez ₊

Ep = "riв     + x2 I dp

E 9

- j rpd E z x ² Ip ⁵⁹

-

ЮЦ 0 d Hz ) p 59 J ’

(5) d H _z ) ^to ц o -r²- I , dp /

A J n ( x a )^{- j}Z^{2 toe 0} J n ( x a ) [             x

Ajn T J n ( x a ) + B

I x a

-

BjZn J n ( x a ) = 0, x 2 a

» J n ( x a ) - Z 2 J n ( x a ) = 0. x]

H p

_ j Гto o d E z

x ² Ip d9

-

H 9

-

x

- j | d E_z в d H fl tos ₀ z + z ² ( dp p 59

.

Записывая условие нетривиальности ее решения (приравнивая нулю главный определитель), получаем дисперсионное уравнение волн круглого экранированного волновода с неидеально проводящей стенкой:

Таким образом, согласно (3)–(6), компоненты поля гибридных волн имеют вид:

^J n ( x a )^{- jZ} 2 — J n ( x a ) ^x

X

E p = - j — J n ( xp ) + Bn ^⁰ Jn, ( xp ) cos n 9 e j ^{в z} ,

I ^x              x p J

E 9 = j An ^ J n ( xp ) + B ^⁰ J n ( xp)l sin n 9 e - j ^{в z} ,

I x2p              x

Ez (p, 9, z) = AJn (xp) cos n9 e-jвz ,(7)

H p =- j [	An toE           B e 2 0 J n ( xp ) +     J n ( xp ) . x p              x         ,	1 sin n 9 e j e z , I
H 9 =- j [	A toE           Bn в 0 J n ( xp ) + 2 J n ( xp )	I cos n 9 e j в z ,

H z ( p , 9 , z ) = B J n ( xp ) sin n 9 e j ^{в z} .

Граничные условия Щукина – Леонтовича в общем случае определяются выражением

[Tn, E] = -Z2 [n [n, TH]] ,(8)

X j -^0- Jn (xa)- Z2 Jn (xa) = [ x_

[„R .]

= Z 2 ^ J n ( x a ) .

[x a_

Решение данного дисперсионного уравнения для нескольких волн круглого волновода с медными стенками отражено на рис. 1. Постоянные распространения, полученные с учетом конечной проводимости медных стенок, на графике неотличимы от значений, получаемых в приближении идеально проводящих стенок.

Сравнение коэффициентов затухания, полученных двумя этими методами (рис. 2), показывает их хорошее совпадение при значениях удельной проводимости 5,8 ■ 10 ⁷ сим/м (проводимость меди). Графики зависимостей, полученных обоими методами, совпадают. Отличие в этом случае составляет не более 0,05 дБ/км.

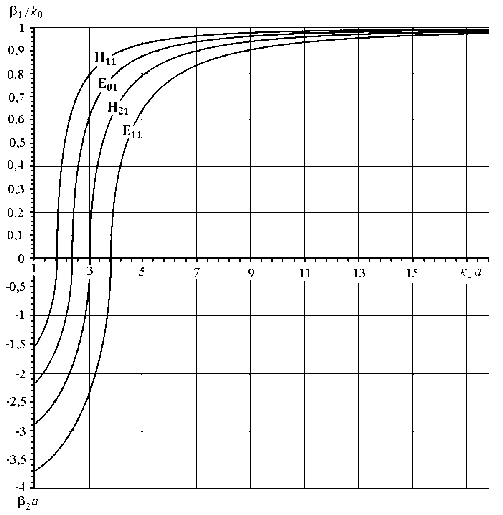
Рис. 1. Зависимости нормированных действительной р 1 и мнимой р 2 частей постоянных распространения первых 4-х волн круглого волновода от нормированной частоты

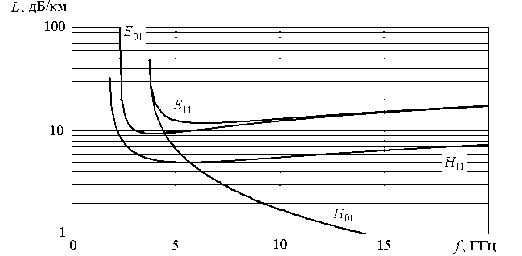
Рис. 2. Зависимости затухания первых 4 волн круглого волновода от частоты. Радиус волновода a = 5 см, удельная проводимость материала стенок волновода ст = 5,8 • 10 7 сим/м

ДЫаДм”1

0,25

0,2

0,15

ОД

0         5         Ю        15      /? ГГц

Наблюдается некоторое занижение величины потерь (растущее с ростом частоты) при использовании метода возмущений.

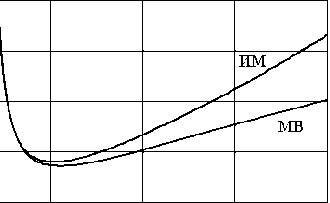
При уменьшении проводимости материала стенок волновода различие коэффициентов затухания становится более заметным. На рис. 3 показаны зависимости коэффициентов затухания основной волны круглого волновода от частоты при удельной проводимости стенок 10 ³ сим/м, полученные импедансным методом и методом возмущений.

Как отмечалось выше, наличие потерь в стенках волновода может приводить к изменению структуры поля. Раздельное существование Е- и Н-волн становится невозможным (за исключением азимутально симметричных). В частности, основная волна круглого волновода H₁₁ становится гибридной или «квазимагнитной» волной. О степени гибридности этой волны можно судить по соотношению амплитудных коэффициентов В и А . На рис. 4 показана зависимость отношения А / В , нормированного на волновое сопротивление свободного пространства, от удельной проводимости материала стенок волновода.

Как видно из рисунка, с уменьшением удельной проводимости материала стенок волновода структура электромагнитного поля меняется. Это изменение необходимо учитывать как при расчете затухания волны в таком волноводе, так и при проектировании устройств возбуждения.

Рис. 3. Зависимости коэффициентов затухания основной волны круглого волновода от частоты. Радиус волновода a = 5 см, удельная прово д имость мат е риала с тенок в о лно вода ст = 10 3 сим/м

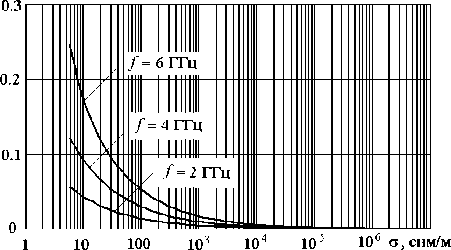
Рис. 4. Влияние удельной проводимости материала стенок волновода на структуру поля основной волны: A – амплитуда E_z ; B – амплитуда Н_z ; Z ₀ – волновое сопротивление свободного пространства