Влияние кросс-поляризации двухполяризационных антенных элементов на эргодическую пропускную способность многоканальной системы

Современные многоканальные радиосредства сверхвысокочастотного (СВЧ) диапазона в качестве приемо-передающих устройств все чаще используют антенные решетки. Для систем беспроводной связи с целью повышения пропускной способности без увеличения апертуры решетки в последнее время применяют двухполяризационные излучающие элементы (кросс-диполи, патчи и т. д.).

При этом зачастую уменьшают расстояние между антенными элементами, что приводит к проявлению эффекта взаимного влияния. В работе [1] выведены соотношения, показывающие, насколько диаграмма направленности (ДН) изолированного антенного элемента будет отличаться от ДН того же элемента в составе антенной ре-

шетки (парциальной диаграммы направленности). В [2] показано, что взаимное влияние может занижать уровень пропускной способности системы.

Однако, кроме искажения диаграммы направленности из-за взаимного расположения элементов, основным фактором, снижающим эффективность системы связи, является наличие пространственной корреляции и кроссполяризации между элементами в составе решетки [3]. Уровень пространственной корреляции зависит в основном от канала распространения, в то время как кросс-поляризация является характеристикой антенной системы и зависит от ее конструкции.

Таким образом, целью работы являлись разработка методики учета поляризационных свойств антенных элементов при расчете эргодической пропускной способности многоканальной систе-

[^^■1 © Аверина Е.В. и др., 2025

мы и исследование влияния поляризационных параметров реальных элементов на пропускную способность различных каналов связи.

1.    Эргодическая пропускная способность системы massive MIMO

Эргодическая пропускная способность системы massive MIMO определяется соотношением [4]:

I

C = -E log 2 det l l + — HH ^h

K L I N o ²

где E L.] - знак усреднения; P - суммарная передаваемая мощность; K – количество пользователей с одной антенной; N – количество элементов антенной решетки; о ² - дисперсия шума; H - канальная матрица.

Для расчета канальной матрицы при проведении аналитических исследований часто используют модель Кронекера. Канальная матрица, исходя из модели Кронекера, может быть представлена следующим образом:

1 / 2         ^{1 / 2}

H = Rrx H0Rtx , где Rrx и Rtx – матрицы взаимных корреляций антенных элементов на приемной и передающей сторонах соответственно, а элементы матрицы H0 – независимые нормально распределенные случайные величины с нулевым математическим ожиданием и единичной дисперсией. В основе модели Кронекера лежит предположение о независимости коэффициентов корреляции для двух антенных элементов на передаче или на приеме соответственно. Корреляция между пользователями, снабженными одной антенной, пренебрежимо мала, поэтому далее предполагается, что Rrx = I, Rtx - R-

Воспользовавшись известными допущениями о свойствах канала и некоторых параметрах системы, в частности предположением, что на решетку воздействуют плоские волны, выражения для элементов введенной матрицы можно записать как функцию геометрических параметров решетки, комплексных диаграмм направленности излучающих элементов и вероятностного распределения углов прихода сигнала. Так для плоской решетки будем иметь:

п/ 2 п

R mn = j f E m (⁰ , ф ) ^Е П (⁰ , ф )^х

-п/2-п х p (0, ф)cos(0)dфd0.

Здесь R mn - элемент матрицы R ; E m ^{( 0 ,} Ф ), E n ( 0 , ф ) - комплексные диаграммы направленности m -го и n -го излучателей с учетом их расположения относительно фазового центра; p ( 0 , ф ) -совместная плотность вероятности углов прихода сигнала по азимуту и углу места. Если считать решетку эквидистантной с расстоянием между элементами d y , d z по горизонтали и вертикали соответственно, плотности вероятности углов прихода по азимуту и углу места независимыми ( p ( 0 , ф ) = = Р 9 ( 0 ) Р ф ( ф )), а диаграммы направленности каждого независимого излучателя равными | E m ( 0 , ф )| = = E n ( 0 , ф )| = | е ( 0 , ф )|, то выражение для коэффициента корреляции между элементами с координатами ( m , n ) и ( k , l ) будет определяться соотношением

R ( m , n , k , l ) =                                                  (1)

п

= j ² _n j exp( j 2 п ( ( m - k ) d y cos( 0 ) sin( ф ) +

+ (n -1)dz sin(0)))p0(0) pф(ф)х х cos(0) | E(0,ф) |2 dфd0.

• 2.    Пространственная корреляция двухполяризационных элементов при наличии кросс-поляризации

Если антенные элементы решетки двухполяризационные, то в таком случае корреляционная матрица будет иметь блочную структуру:

^R Vv ^R Vh R hv R hh

где через нижние индексы обозначена поляризация соответствующих элементов. В отсутствие кросс-поляризации между элементами матрица будет иметь вид

R =

R _vv 0

R _hh

где значения элементов матриц-блоков R vv , R hh определяются выражением (1). Найдем значения элементов матриц-блоков из (2) через поляризационные свойства излучающих элементов с учетом наличия кросс-поляризации.

Кросс-поляризация между двумя различными портами двухполяризационного излучающего элемента обычно описывается параметром XPI , который определяется соотношением

- ₌ Evv ( 6 , ^ф) _{ypJ =} Ehh (⁹ > Ф ) v = E vh ( 6 , ф ) ^{,        h} = E hv ( 6 , ф ) ^,

E_v ² XPI_v ²

1 + XPI v

+- E h -, ¹ + ^XPI h

где E vv , E_vh , E_hh , E_hv - со-поляризационная и кросс-поляризационная диаграммы направленности каждого порта соответственно. Из определения видно, что в общем случае параметры XPI v , XPI_h являются функциями азимута и угла места, но при дальнейшем выводе мы опустим эту зависимость. Тогда для расчета кросс-поляризационной компоненты диаграммы направленности элемента можно воспользоваться соотношениями:

^E h ^E h =

к

E vh =

E vv

/XPI v ’   ^hv

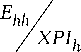
Сначала найдем нормировочные множители для каждого порта, удовлетворяющие условию сохранения излучаемой мощности:

E v = E h (1 + XPI v h E h =         ,

V1 + XPI 2

XPIv Ev

1 + XPI v

E h = E hv (1 + ^XPI h h E hv =           ^,

V i + xpi 2

XPI h E h

E hh              ,

V¹+ ^xpi h

Здесь E v , E h - диаграмма направленности одно-

поляризационного элемента.

Напряженность поля каждой компоненты с учетом эффекта кросс-поляризации:

^E v

= E vv

E v XPI v

⁺ E hv    I 7

1 + XPI h

+               ,

V¹+ XPI h

' E h = E hh		+ e, = E h kpi h l +_	Ev
		vh 1 + xpi h 1 + + xp^
'     1* E v E h =		Ev\XPIv\ +     E h	x
	к	j 1 + XPI v 1+ + XPih ?

E h l ^XPI h l ₊

¹ + ^XPI h

E h ^Xpi h ₊   E ^h

1 + xpi h 1 + xpi v

•

Ev

1+xpih v 7

При выводе мы воспользовались условием

*

*

E v E h = E h E v = 0.

Тогда коэффициенты корреляционных матриц-

подблоков (2) будут иметь вид

R ’ vv ( m,n, k, l ) = п/h n

= J J exp( j h n ( ( m - k ) d y cos( 6 ) sin( ф ) +

-n/ h -n

+ ( n - 1 ) d z si^{n( 6 )))} p ₆ (⁶) p ф ( ф ) cos^{( 6 ) x} x | E v ( 6 , ф ) |^h d ф d 6 =

XPI_v ²

1 + xpi.

T Rvv +        Rhh, h     1 + XPIh

R' hh (m,n,k, l ) = п/h n

= J J exp( j h n ( ( m - k ) d y cos( 6 ) sin( ф ) +

-n/ h -n

+ ( n - 1 ) d z sin( 6 ))) p ₆ ( 6 ) p ф ( ф ) cos( 6 ) x x | E h ( 6 , ф ) |^h d ф d 6 =

XPI h ²

------7 R hh ^{+ 1} + ^XPI h

1 + XPI

о R vv , ²

v

R' vh (m, n, k, l) = R' hv (m, n, k, l) = n/h п

= J J exp( j h n ( ( m - k ) d y cos( 6 ) sin( ф ) +

-n/ h -n

+ ( n - 1 ) d z sin( 6 ))) p ₆ ( 6 ) p ф ( ф ) cos( 6 ) x x E v ( 6 , ф ) E h ( 6 , ф ) d ф d 6 =

E h l XPI h I ₊     E v

J 1 + xpi 2 J 1 + xpi ² ^      h \      v

= E hI XP v l₊ E h J XP y 1 + xpi v 1 + xpih ’

XPI v

1 + xpi

hl R vv ⁺ v

XPI h

1 + XPI

T R hh • h

Если допустить, что XPI v = XPI h = XPI = const, R _vv = R hh , то для выражения (h) получим

' I*

E E vv

E v XPI v l ₊

R _vv

J 1 + xpi h к v v

1 + xpih,

R ‘ =

2 XPI

L 1 + xpi

2 R vv

2 XPI

R _vv

1 + XPI ^h

R vv

.

Итак, для расчета матрицы пространственной корреляции двухполяризационной антенной решетки с учетом кросс-поляризации необходимо иметь со-поляризационные диаграммы направленности и значения XPI v , XPI h • Если эти значения являются функциями углов, то при расчетах необходимо использовать соотношения (3)–(5). Если эти значения являются постоянными величинами, то можно воспользоваться соотношениями (6)–(8). И наконец, при равенстве со- и кросс-поляризационных свойств портов различной поляризации для расчетов применяется соотношение (9).

Из соотношения (9) видно, что если кроссполяризация у двухполяризационного элемента незначительная ( XPI ^ » ), то пространственная корреляция между элементами разной поляризации стремится к нулю. При наличии кроссполяризации из-за увеличения пространственной корреляции уменьшается число степеней свободы системы, что приведет к уменьшению ее разрешающей способности.

Воспользовавшись выведенными соотношениями и моделью Кронекера методом Монте-Карло, рассчитаем зависимость пропускной способности для плоской антенной решетки размером 4 х 8 с расстояниями между элементами d y = 0,5 Х , d z = 2 Х от величины кросс-поляризации XPI • В качестве антенного элемента использовался идеальный двухполяризационный патч с поворотом плоскости поляризации ± 45 ° . Вероятностное распределение углов прихода по углу места описывалось законом Лапласа, по азимуту – законом фон-Мизеса. При расчете использовались допущения для выражения (9). На рис. 1 представлена полученная зависимость. Видно, что уменьшение XPI ниже 10 дБ приводит к уменьшению пропускной способности системы.

3.    Моделирование с реальными излучающими элементами

Для оценки величины кросс-поляризационного параметра XPI реальных антенных элементов и его влияния на пропускную способность в среде CST Studio Suite были синтезированы модели двухполяризационного двухпортового stacked патч-элемента [2] и кросс-дипольного элемента с поляризациями ± 45 ° .

Полученные с помощью электродинамического моделирования путем решения системы урав-

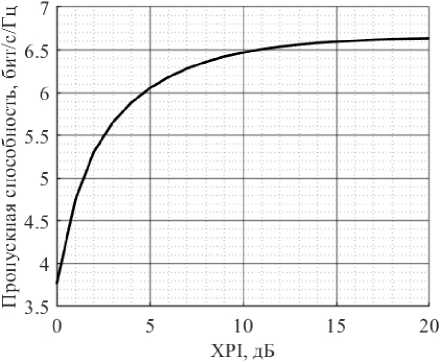
Рис. 1. Зависимость эргодической пропускной способности от уровня кросс-поляризации

Fig. 1. Dependence of ergodic capacity on the level of crosspolarization

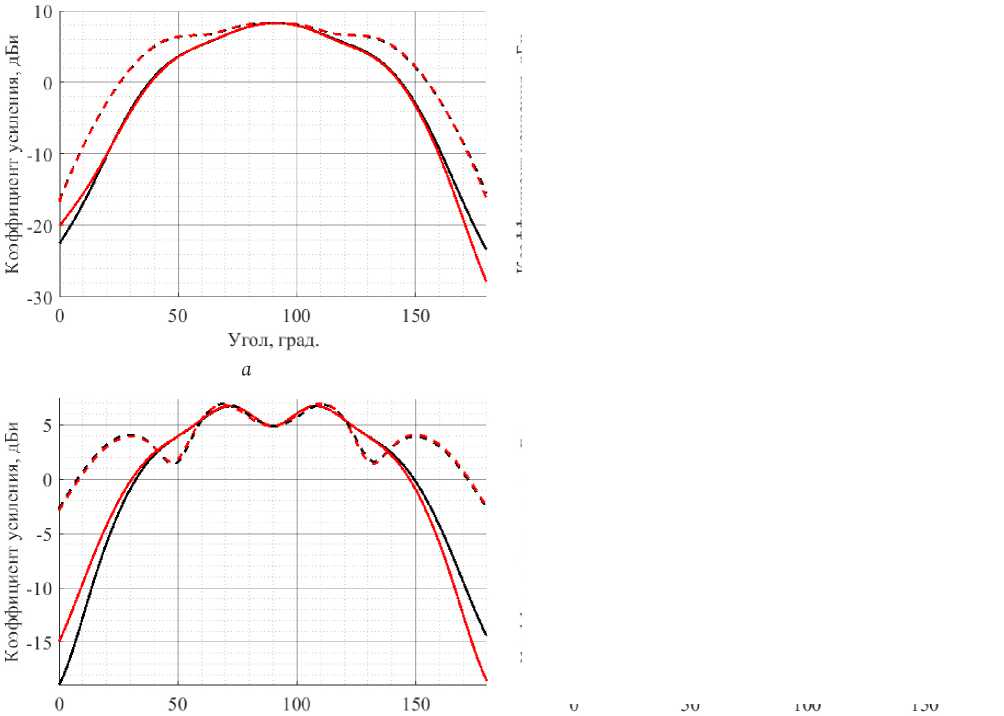
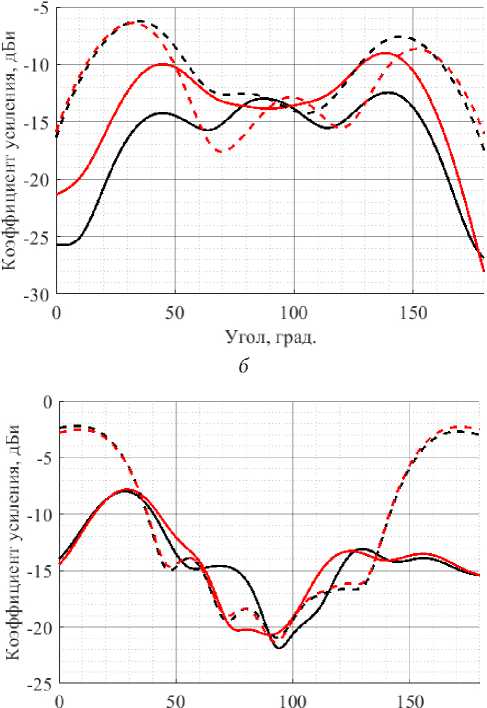
нений Максвелла (метод моментов) диаграммы направленности: со-поляризационная и кросс- поляризационная для каждого порта представлены на рис. 2.

Видно, что со-поляризационные диаграммы каждого элемента совпадают между собой в направлении основного излучения. Поэтому можно считать, E vv = E hh = E ( 0 , ф ).

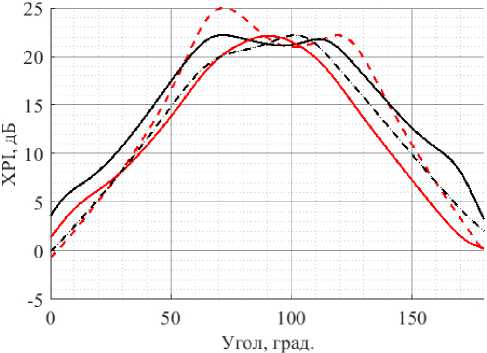
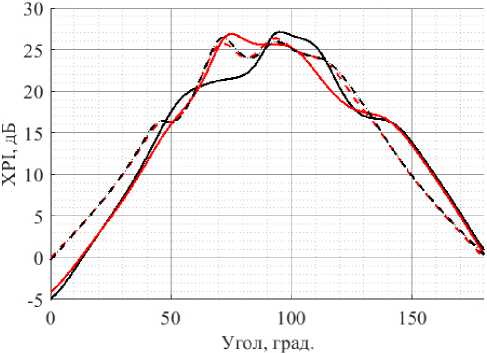
На основе полученных диаграмм направленности порта каждой поляризации были рассчитаны угловые зависимости XPI v , XPI h для кросс-дипольной и патч-антенны (рис. 3).

Из рисунка видно, что зависимости для XPI v и XPI h для с графической точностью совпадают как для патч-элемента, так и для кросс-дипольного элемента. Незначительное отличие в видах XPI v и XPI h для кросс-дипольного элемента можно объяснить несимметричностью его системы запитки.

Таким образом, можно считать, XPI v = XPI h = = XPI ( 0 , ф ). И наконец, XPI сложным образом зависят от 0 , ф . Исходя из этого, соотношения для расчета элементов матрицы пространственной корреляции будут иметь вид

R Vv = R hh = R vv ,

R' vh (m, n, k, l) = R' hv (m, n, k, l) = п/2 n

= J J exp( j 2 n ( ( m - k ) d y cos( 0 ) sin( ф ) +

• -п/ 2 -п

+ (n -1)dz sin(0)))p0 (0) pф (ф) cos(0) х х E2 (0, ф)

2 х XPI ( 0 , ф ) d ф d 0 .

1 + XPI ² ( 0 , ф )

Угол, град.

Угол, град.

в г

Рис. 2. Диаграммы направленности кросс-дипольного ( а – со-поляризационная, б – кросс-поляризационная компоненты) и stacked – патч-элементов ( в – со-поляризационная, г – кросс-поляризационная компоненты) для первого (черная линия) и второго (красная линия) порта. Пунктирной линией обозначены срезы вдоль направления поляризации порта, сплошной – перпендикулярно)

Fig. 2. Antenna patterns of cross-dipole ( a – co-polarization, b – cross-polarization components) and stacked-patch elements ( c – copolarization, d – cross-polarization components) for the first (black line) and the second (red line) port. Dotted line indicates slices along the direction of port polarization, solid line – perpendicular)

а                                                    б

Рис. 3. Диаграммы XPI кросс-дипольного ( а ) и stacked – патч-элементов ( б ) для первого (черная линия ( XPI_h ) и второго (красная линия ( XPI_v )) порта. Пунктирной линией обозначены срезы вдоль направления поляризации порта, сплошной – перпендикулярно) Fig. 3. XPI patterns of cross-dipole ( a ) and stacked-patch elements ( b ) for the first (black line ( XPI_h ) and the second (red line ( XPI_v )) port. Dotted line indicates slices along the direction of port polarization, solid line – perpendicular)

Таблица. Эргодическая пропускная способность антенной решетки с реальными антенными элементами Table. Ergodic capacity of an antenna array with real antenna elements

С без учета кроссполяризации, Бит/c/Гц С с учетом кроссполяризации, Бит/c/Гц Л C, % Кросс-диполь 6,884 6,869 1 Патч 6,641 6,616 1 элементов антенной решетки. Это позволит оптимальным образом подобрать излучающие элементы для заданной системы. На основе анализа с помощью выведенных соотношений установлено, что влияние кросс-поляризационных свойств антенных элементов решетки на пропускную способность многоканальной системы связи становится значительным при снижении величины кросс-поляризационного параметра ниже 10 дБ. Показано, что синтезированные реальные антенные элементы различного типа обладают высокой развязкой по поляризации, что приведет к незначительному снижению пропускной способности системы. Это позволяет их использовать в качестве излучателей для многоканальных систем связи на основе антенных решеток.

Финансирование

Исследование выполнено за счет гранта Российского научного фонда № 24-19-00891,

Для выполнения численных расчетов в работе использовалось оборудование учебно-научного дизайн-центра проектирования радиоэлектронных систем СВЧ, терагерцового и оптического диапазонов на отечественной электронной компонентной базе ФГБОУ ВО «ВГУ» в рамках реализации федерального проекта «Подготовка кадров и научного фундамента для электронной промышленности».