Влияние магнитного поля на свойства поверхностных поляритонов на границе «полупроводник-диэлектрик»

• 1.    ВВЕДЕНИЕ

• 2.    ГЕОМЕТРИЯ ЗАДАЧИ И ОСНОВНЫЕ СООТНОШЕНИЯ

Известно, что в области частот, где диэлектрическая проницаемость (ДП) одной из граничащих сред отрицательна, вдоль плоской границы раздела двух немагнитных диэлектриков возможно распространение электромагнитных поверхностных волн, получивших в литературе название поверхностных поляритонов (ПП) [1, 2]. Поле такой волны экспоненциально убывает при удалении от границы раздела. В среде с отрицательной ДП это связано с мнимостью поперечной компоненты волнового вектора, а в среде с положительной ДП – с полным внутренним отражением. В настоящее время исследования свойств ПП на границе раздела различных сред развиваются достаточно динамично, что обусловлено их уникальными свойствами: высокой пространственной локализацией и возможностью значительного усиления напряженности волнового поля вблизи границы раздела сред. Толщина приповерхностного слоя, в котором локализуется волновое поле ПП, с каждой стороны от границы раздела обычно составляет величину порядка длины волны. Свойства ПП во многом определяются материальными параметрами и состоянием граничных сред, поэтому отвечающие им решения волновых уравнений широко используются для изучения оптических свойств различных материалов [3-9].

Различные планарные полупроводниковые

структуры представляют существенный интерес для многих направлений микроэлектроники, поэтому изучение спектра поверхностных волн на границе полупроводник-диэлектрик является актуальной задачей. Особую роль в формировании ПП играет внешнее статическое магнитное поле, которое приводит к гиротропии намагниченного полупроводника [10-14]. Поскольку материальные параметры намагниченного полупроводника существенно зависят от частоты и магнитного поля, то существенна и модификация волновых характеристик ПП, возникающая при изменении управляющего магнитного поля. В настоящей работе, наряду с обсуждением условий существования ПП на границе намагниченного полупроводника и диэлектрика, получены и детально анализируется дисперсионное соотношение, определяющее связь волновых характеристик поляритона с магнитным полем. Анализ проводится для широко используемой в различных практических приложениях плоскостной поперечной ориентации магнитного поля, при которой поле лежит в плоскости границы раздела сред и перпендикулярно направлению распространения ПП.

Направим ось OZ перпендикулярно границе раздела сред, а ось OX вдоль направления распространения волны. Будем считать, что область z < 0 занята изотропным диэлектриком со скалярной ДП £d, а область z > 0 занята полупроводником с тензорной ДП £s. Магнитные проницаемости обеих сред будем считать равными единице. В полупроводнике при нали- чии внешнего магнитного поля, ориентированного вдоль оси ОY, проявляется анизотропия оптических свойств. В этом случае тензор ДП полупроводника принимает вид:

Здесь введены волновое число для вакуума k 0 = ю / С , поперечные компоненты волнового вектора в каждой из сред:

A

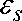
( £s 0 i£a

О ^£ s 0 ⁰ v- ^{i £} a ^{0 £} s J

где частотные зависимости элементов этого тензора, характерные для намагниченной плазмы имеют вид [14]:

£ = £

1+

V

ю r - ю

c

,

г Л ю„

^£ s 0

= £, 1 — -pr

V

ю J

^£ sa

^£ 0

ю2 ю pc

ю(ю2

-

ю2)

.

Здесь £ 0

– решёточная часть ДП полупро-

водника, ю p

/           2       * \1/2

= ( 4 n ne / m )

–

плазменная

частота, ю _с = eH 0 / m * С — циклотронная частота, H – внешнее магнитное поле, n – кон *

-

-

центрация носителей (электронов), e и m - заряд и эффективная масса электрона, c – скорость света в вакууме. Соотношения (2) записаны в приближении отсутствия потерь, связанных со столкновениями.

Собственными волнами такой структуры при распространении волны вдоль оси OX являются ТМ и ТЕ волны. Зависимость каждой из

компонент волнового поля от времени и коор динаты x может быть представлена в виде:

F _a ( t , x , z ) = F _a ( z ) exp[ i( to t - p x )] ,(3) где в — продольная компонента волнового век тора (константа распространения) ПП. Для уп равляемой магнитным полем ТМ волны с компо

-

-

-

нентами волнового поля ( Ev, H,, E,) запишем xyz уравнения для тангенциальных (относительно границы раздела) компонент в каждой из сред:

d2 H

y dzz

- q 2 h = 0

1 d , s У

Qd = 4в -k02£d,    qs = 7в -k02£L,(5)

а также - эффективная ДП полупроводника

„     „ _ 2 / „

. Решения волновых уравне-

1 s a s                          U ний (4) для компоненты магнитного поля Hy в областях, занятых полупроводником и диэлект-

риком, с учетом ее непрерывности на границе раздела представим в виде:

H y ( z ) = H (0) ■

^exp ( ^- q s z ) , ^exp ( Q d z ) ,

z <  0. ⁽⁶⁾

где H (0) - амплитуда поля в плоскости раздела сред (при z = 0 ). Для определения областей существования ПП необходимо потребовать действительности величин q s и q d , что выражается следующими условиями:

qs = в2 — к0£1>0, qd = в2 — k02£d > 0. (7)

Используя непрерывность на границе раздела сред тангенциальной компоненты магнитного поля H y , приходим к дисперсионному соотношению:

Qd + Qs = £^ в

^£ d    ^£ 1    ^£ s ^£ 1 .

В отсутствие внешнего магнитного поля ( H 0 = 0 ) исчезает гиротропия полупроводника ( £ a = 0 , £ 1 = £ s ) и соотношение (8) переходит в известное дисперсионное уравнение для изотропных диэлектриков

Qd /£d + Qs /£s = 0.           (9)

Из этого соотношения следует, что условием существования ПП в этом случае является отрицательность ДП одной из контактирующих сред [1, 2].

При наличии магнитного поля дисперсионное соотношение (8) с учетом выражений (7) приводится к виду

^£ d ^£ s         ^k 0 ^£ 1

Ex = '

^k 0 ^£ d

У ’

Z7 _ i(£аЗ — £sQs ^U

Ex = ^Г£2ТH'(4)

= ^£ d ^£ a ^в — ^£ s ^£ 1 j^в — ^k 02 ^£ d . ⁽¹⁰⁾

Наличие в этом уравнении слагаемого, линейного по параметру в , указывает на тот факт, что наличие магнитного поля приводит к невзаимному характеру распространения ПП в рассматриваемой структуре. При H 0 = 0 невзаимность исчезает и константа распространения ПП определяется соотношением

в(—) = ±ко -c

£d£s —)

Ed + £s —) '

Поверхностная волна переносит вдоль границы раздела сред энергию волнового поля. Усредненная по времени плотность энергетического потока в каждой из сред в рассматриваемом случае определяется вектором Пойнтинга:

S = — Re ( EH _уe - EH _уe, ) . (12)

xyz zyx

8п

В отсутствие поглощения в обеих средах составляющая потока S = 0 . С учётом граничных условий получаем для продольных компонент плотности потока энергии в каждой из сред:

ев - eq sas

c

S x ="

H (0)

8 n k ₀

^£ _s ^£ l

exp( - 2 q s z ), z >  0,

— ^exp⁽² q_dz ), I ^E d

(13) z <  0.

3. ГРАНИЦА «ЛИНЕЙНЫЙ

ПОЛУПРОВОДНИК-ДИЭЛЕКТРИК»

Определим теперь некоторые характерные зависимости и частоты, которые проявляются при графическом построении и анализе дисперсионного соотношения для ПП. Так, в общем случае эффективная ДП полупроводника £ ₁ меняет знак на следующих трех частотах:

ветвям зависимости — = с в / \£ у в областях в >  0 и в <  0 соответственно. Кривые С и С 2 пересекают ось частот в точках — 1⁺ .

Для проведения численного моделирования характеристик поверхностной волны в рассматриваемой структуре в качестве диэлектрика выбран фторопласт с £ d = 2.23, а в качестве полупроводника - антимонид индия (InSb), для которого решеточная часть ДП £ 0 = 17.8 , плазменная частота — p = 10¹² s^-1, эффективная масса электрона m * = 0.014 m , где m e - масса покоя электрона [14]. На графиках мы используем безразмерную частоту Q = — / — p , поэтому приведенным выше характерным частотам отвечают величины, нормированные на плазменную частоту.

На рис. 1 приведена зависимость нормированной частоты от константы распространения, полученная для подмагничивающего поля H 0 = 50 Oe. Дисперсионная ветвь D 1 , отвечающая положительным значениям константы распространения, лежит в интервале частот 0 < Q < Q + . Ветвь D 2 , которая отвечает отрицательным в , лежит в интервале 0 < Q < Q ^- . При стремлении Q ^ Q ± должно иметь место существенное замедление ПП, так как его групповая скорость d — / d в ^ 0 . Несимметрия дисперсионных кривых при смене знака константы в , которая указывает на невзаимный характер распространения ПП. В пределе H ₀ ^ 0 невзаимность пропадает,

—

'± = j (V—2 + 4-2 ± -с ),

— + — .

pс

Возвращаясь к условиям существования ПП (7), отметим, что первое из них ( q s >  0 ) распадается на два возможных случая: при £ ^ <  0 ему удовлетворяют все действительные значе-

ния в в частотных интервалах от 0 до — 1 и от — s до — 1 + ; при £ _± >  0 это усл овие эквивален-

тно неравенству

Условие

0      ^

q d >  0 в случае положительных £ d эквивален-

Дисперсионное соотношение (10) в общем

случае имеет четыре решения, которым на представленных ниже графических зависимостях отвечают четыре ветви D 1 - 4 (сплошные кривые). Пунктирные линии А 1 и А 2 отвечают ли-

нейной зависимости

— = св /

^£ d

в областях

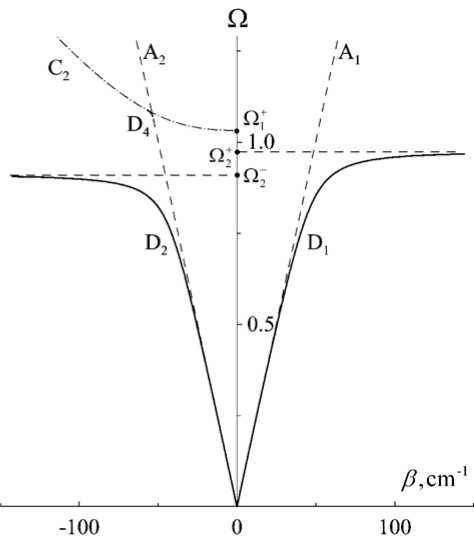
Рис. 1 . Дисперсионные зависимости для поверхностных ТМ волн;

Н₀ = 50 Oe; е ₀ = 17.8, w _P=10¹² s^-1

в >  0 и в <  0 . Пунктирные кривые С и С 2 отвечают низкочастотной и высокочастотной

т.е. низкочастотные ветви D 1 и D 2 становятся симметричными и при стремлении в ^ ± го ограничены значением частоты Q 0 — ^ O^^ ^^+^ d )) . В интервале частот Q 2 + в структуре возможно распространение только одной – прямой волны. Частоты, к которым дисперсионные кривые D 1 и D 2 асимптотически стремятся при в ^ ± го , являются для гиротропных полупроводников аналогом частоты Деймана-Эшбаха [15] и определяются следующими выражениями:

Q± —

1

2®

p

к

2   ⁴ ®^£

й)„ +

d 0

\

® h . (15) J

В высокочастотной области проявляется ветвь D 4 , которая ограничивается сверху кривой С 2 , а снизу линией A 2 и отвечает обратным волнам, т.е. в <  0 • В отсутствие поля эта ветвь также отсутствует, а с увеличением поля частотный интервал ее существования увеличивается. Обратим также внимание на тот факт, что для используемого значения поля частота Q + < Q s и в спектре отсутствует высокочастотная ветвь D 3 . Таким образом, появление в спектре ветви D 4 и невзаимности является следствием возникновения индуцированной подмагничивающим полем гиротропии полупроводниковой среды.

На рис. 2 представлены дисперсионные зависимости Q ( в ) , отвечающие значению поля H о — 308 Oe. Это значение больше критического

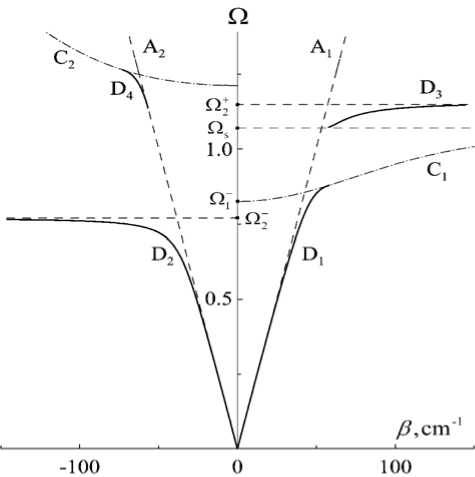
Рис. 2. Дисперсионные зависимости для поверхностных ТМ волн; H₀ = 308 Oe

H — 2d ®-с' 4^ y ■ (16)

получаемого из условия ® 2 — m s (здесь у — e / m c - эффективное гиромагнитное отношение). Для выбранных параметров структуры H с _г = 100 Oe. Отметим, что при значении поля H о ^ H cr частота Q s < Q + . При значении поля H — H сr происходит разделение ветви D 1 на низкочастотную и высокочастотную, в

Рис. 3 . Полевые зависимости константы распространения низко- и высокочастотных ПЭВ, £ 0 = 17.8, to p = 10¹² s ' ¹; ® =(0.75, 1.15) - 10¹² s^-1 (а, b ) ной области при малых значениях поля в структуре могут распространяться две собственные волны с противоположными знаками константы в и отвечающие ветвям D 1 и D 2 . Поле, при котором константа распространения обратной волны (ветвь D 2 ) уходит на бесконечность, определяется выражением:

результате чего в спектре проявляется новая дисперсионная ветвь D 3 , располагающаяся при в >  0 в высокочастотной области спектра. Эта

ветвь ограничена узким интервалом частот Q s ( H ₀) < Q < Q + ( H ₀) , который при значении поля H ₀ — H сr стягивается в точку. Частотный интервал существования ветви D 4 при заданном значении поля оказывается больше,

чем на предыдущем рисунке.

На рис. 3 приведены полевые зависимости константы распространения, построенные для низко- и высокочастотных поверхностных волн при ® = (0.75, 1.15) - 10¹² s^-1 ( а, b ). В низкочастот-

H 2

^£ d    ® 2

£d + £ 0 ®

- to

Для частоты to = 0.75 . 10¹² s^-1 это поле составляет 346 Oe. Выше этого значения поля в структуре возможно распространение только прямой волны, соответствующей ветви D₁. Ветвь D₁ исчезает при пересечении с кривой C 1 , после чего на данной частоте в структуре ПП не распространяются. В высокочастотной области прямая волна в интервале полей ( 0, H 2 ) отсутствует, отвечающая ей ветвь D 3 уходит на бесконечность при значении поля H 2 ® 300 Ое. В интервале H 0 = (300 – 336) Oe могут существовать две встречных волны с отличающимися по модулю константами распространения, что открывает возможность для создания различных невзаимных устройств.

На рис. 4 для двух значений поля H 0 = (308, 630) Oe ( а, b ) и различных частот приведены распределения по поперечному сечению структуры продольной компоненты плотности потока энергии, переносимой ПП. При построении указанных распределений используется нормированная на вакуумную длину волны ( X = 2 n c / to ) координата z . Кривые 1,2 отвечают ветвям D₁, D₂ , а кривые 3,4 отвечают ветвям D₃, D₄ . На рис. 5 а частоте to = 0.75 • 10¹²s ^{- 1} отвечают кривые 1,2, а частоте _ю = 1_.1 5 • 10¹² s ^{- 1} - кривые 3,4. На рис. 5 b кривые 1,2 отвечают частоте to = 0.5 • 10¹²s ^{- 1} , а кривые 3,4 - частоте to = 1.3 7 • 10¹²s ^{- 1} • Из

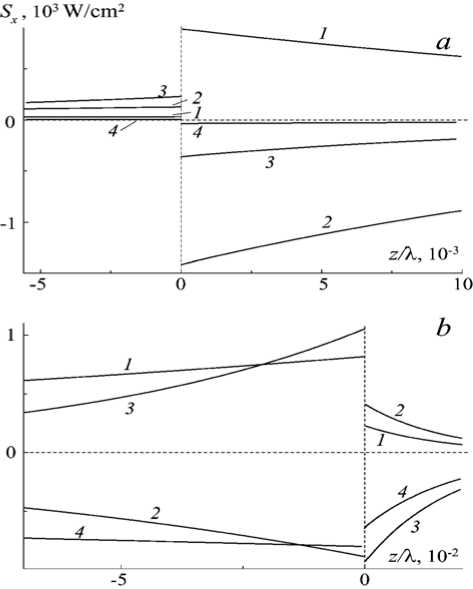
Рис. 4 . Распределение плотности энергии ПЭВ от нормированной координаты при значениях поля H₀=308, 630 Oe (а, б)

приведенных зависимостей следует, что продольная компонента полного потока претерпевает разрыв на границе раздела, при этом в граничащих средах для ПП они различаются знаками. В диэлектрической среде с положительной ДП S x -компонента потока совпадает по направлению с фазовой скоростью. В полупроводниковой среде, где в области существования ПП проницаемость отрицательна, S x -компонента потока противоположна по направлению фазовой скорости. Изменение поля может приводить к существенному перераспределению величины S x . Так, в рассмотренном случае при малом значении поля H 0 волновое поле ПП вблизи границы раздела в полупроводнике значительно превосходит поле в диэлектрике, тогда как при больших значениях поля картина меняется на противоположную.

4. ГРАНИЦА «НЕЛИНЕЙНЫЙ ПОЛУПРОВОДНИК-ДИЭЛЕКТРИК»

Пусть теперь область z >  0 занята нелинейным полупроводником с тензорной ДП и параметром нелинейности X :

8NL = 8, + X E21,      <18)

где элементы этого тензора имеют частотные зависимости вида (2).

Решение уравнений (4) в виде поверхностной волны, локализованной на границе раздела сред z = 0 , с учетом нелинейности среды в области z >  0 представим для тангенциальной компоненты электрического поля в виде:

E x ( z ) Н

A sech [ q_s ( z - z ₀) ] , z >  0,

E 0 exp( q ^ z ),         z ^ 0 ,

где E 0 – амплитуда поля на границе раздела сред, а параметр A = ^2 q 2 / x k 02 • Условием существования поверхностной волны, в соответствии с (19), является действительность поперечных компонент q s и q d волновых векторов в каждой из сред. С учетом их определения получаем следующие ограничения на значения константы распространения ПП: | ^ >  k ₀ .^d и | ^ >  к ₀^ 6 7 для частотной области, где 8 _± >  0 ; для частотной области, где 8 _±<  0 , требование q² >  0 подобных ограничений не накладывает.

Параметр z 0 определяет положение (т.е. смещение относительно границы раздела сред z = 0 ) максимума амплитуды волнового поля в полупроводнике. Согласно (19), смещения описывается уравнением

A sech( q s z 0 ) = E 0 ,       (20)

решение которого определяется выражением

( z0 = —ln

⁰ q s

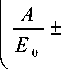
E

A

² ^

- 1

Видно, что наряду с положительным смещением указанного максимума, возможно также отрицательное его смещение. Знак влияет на форму распределения поля в ПВ.

На рис. 5 представлена зависимость параметра от амплитуды волнового поля, полученные для трех значений магнитного поля H0= (308, 630, 950) Э (кривые 1 - 3). При zо > 0 максимум распределения амплитуды поля в структуре находится в области, занятой полупроводником. При zо < 0 максимум этого распределения смещается в область, занятую диэлектриком, поэтому он не проявляется, а наибольшего значения амплитуда ПВ в этом случае достигает на границе раздела сред. На рис. 6 представлены распределения электрического поля поверхностной волны по нормали к границе раздела сред, полученные на частоте ю = 7.65 • 1011 с-1 для значений поля H0 = (308, 630, 950) Э (кривые 1 - 3) при в = 50 см-1, E0 = 1.5 эрг / см3 .

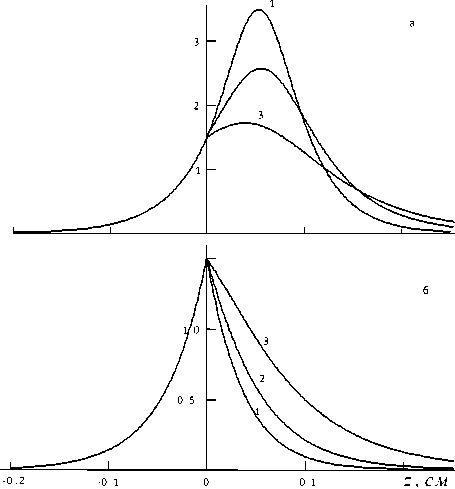
Рис. 5 . Зависимость параметра z 0 от амплитуды волнового поля; H 0 = (308, 630, 950) Э (кривые 1 - 3)

В случае z 0 = 0 в соответствии с (21) выполняется условие E 0 = A , которое выражается уравнением

(%Е 02 + 2е ± )ю2 = 2 c2 в2. (22)

С учетом (19) и (20) для тангенциальной компоненты магнитного поля ТМ волны в каждой из сред получаем следующие выражения:

H ^y

kA ^sech [ q , ⁽ z - ^z 0 ) L^ee a ⁺ q , ^e - ^th ( q - ^{( z - z} 0 ) ) ] ^{, z - 0},

K k e E                    (23)

⁰ d ⁰ exp( q d z ),                   z <  0.

iqd где параметр z0 может быть как больше, так и меньше нуля. Равенство тангенциальных компонент магнитного поля на границе раздела сред (при z = 0) приводит к дисперсионному соотношению qs£s th (q,z0 )= Р£а + ^^K2,(24) qd которое с учетом (20) можно записать также в следующей форме:

E t ^ ⁺ £ a q a P + £_s q _s q a^ ^{1 -} E ² / ^{A 2 -} £_s£ d k 0 = ⁰. ⁽²⁵⁾

Здесь знак «минус» перед третьим слагаемым соответствует положительным значениям , а знак «плюс» – отрицательным. Переход от одного дисперсионного соотношения к другому происходит через семейство кривых

Edв + £a4dв - £desk02 = 0, (26)

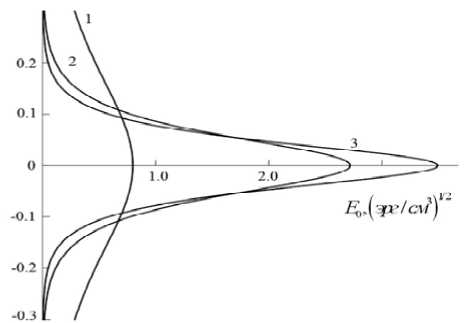
Рис. 6 . Распределения поля поверхностной волны по нормали к границе раздела сред;

ю = 7.65 • 10¹¹ с^-1, H 0 = (308, 630, 950) Э

(кривые1-3), в = 5 0 см^-1,

E ₀ = 1.5    эрг / см ³

отвечающих равенству . Наличие в дисперсионных уравнениях (24)-(26) слагаемого, пропорционального первой степени константы распространения, указывает на сохранение невзаимного характера распространения ПП и в структуре «нелинейный полупроводник-диэлектрик».

ЗАКЛЮЧЕНИЕ

В работе для плоской границы раздела намагниченного полупроводника с заданной частотной зависимостью тензорной ДП и диэлектрика с независящей от частоты ДП определены частотные области существования ПП. Наличие поперечного (по отношению к направлению распространения) внешнего поля приводит к линейному двулучепреломлению и зависимости волновых характеристик ТМ-поляритона от магнитного поля. При положительности ДП диэлектрика ПП реализуется в частотных областях, где эффективная ДП полупроводника отрицательна. Вычислены характерные частоты, определяющие области существования TM-поляритона, которыми можно управлять с помощью внешнего магнитного поля. Проведенный анализ показал, что для используемых параметров структуры ПП в общем случае имеет четыре ветви дисперсионной зависимости о(в') , Две из которых отвечают прямым волнам, а две – обратным. При стремлении Q ^ Q± групповая скорость ПП dm/dв ^0, т.е. имеет место существенное замедление ПП. Несимметрия дисперсионных кривых при смене знака константы β указывает на невзаимный характер распространения ПП. Установлено, что продольная компонента потока энергии в каждой из сред испытывает разрыв на границе раздела сред. Эта компонента в диэлектрической среде совпадает по направлению с фазовой скоростью, тогда как полупроводни- ковой среде, где в области существования ПП эффективная ДП отрицательна, противоположна по направлению фазовой скорости. Изменение поля приводит к существенному перераспределению потока в каждой из сред и полного потока в структуре.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральных целевых программ «Научные и научно-педагогические кадры инновационной России на 2009 - 2013 годы» и «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007-2013 годы»