Влияние многолучевости при распространении радиоволн в минисотовых системах

Рассмотрим случай, когда от БС до здания распространяется прямая волна и отраженная от Земли (рис. 1).

Рис. 1. Расположение антенн вне зданий (двухлучевая аппроксимация)

Данный случай наиболее распространен и является типичным в городских условиях для минисотовых сетей.

Угол падения волны будет изменяться в зависимости от высоты антенны БС, высоты антенны АРБ и расстояния между ними. Исходя из геометрических соотношений, угол падения волны можно вычислить по формуле

π      ⎛ h+h

φ ( l,h₁,h₂ ) = ₂ - arctg _{⎜ ⎝} ¹ _l ²

Длины путей прямого и отраженного распространения также зависят от указанных параметров и будут, соответственно, равны ri (1, hi, h 2 ) = V( h 2 - hi )2 +12

r₂ ( 1 , h 1 , h 2 ) = V ( h 2 + h 1 ) ² + 1 ²

В рассматриваемом случае h₁ >> отражение осуществляется от полупроводящей поверхности Земли. Коэффициент отражения для вертикально и горизонтально поляризованной волны могут быть найдены из выражений [1]. Результирующая напряженность поля в точке приема (Е^· ) складывается из напряженности прямой волны (Е^·_пр) и напряженности отраженной волны (Е^·_отр)

Е^· С = Е^· пр + Е^· отр (1).

При мощности P₁ , подводимой к передающей антенне БС, и коэффициенте усиления G₁ = 1 в точке приема напряженность электрического поля прямой волны [1]

Eпр = -0PeXPP r1

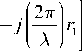
Отраженная волна распространяется по пути r2 и создает в точке приема напряженность электрического поля [1]

отр

F exp r₂

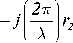
где F^· — комплексный коэффициент отражения.

Отсюда, используя выражения (2), (3), получим

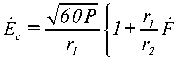
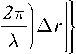
(4),

где Δ r = r₂ — r₁ — разность хода прямой и отраженной радиоволн.

Выражение внутри фигурных скобок (4) называют комплексным множителем ослабления в освещенной зоне [2, 3]

W = 1 + r F' exp r₂

⎛ 2 π ⎞

- j Δ r ⎜ ⎝ λ ⎟ ⎠

Модуль множителя ослабления согласно (5) будет иметь вид

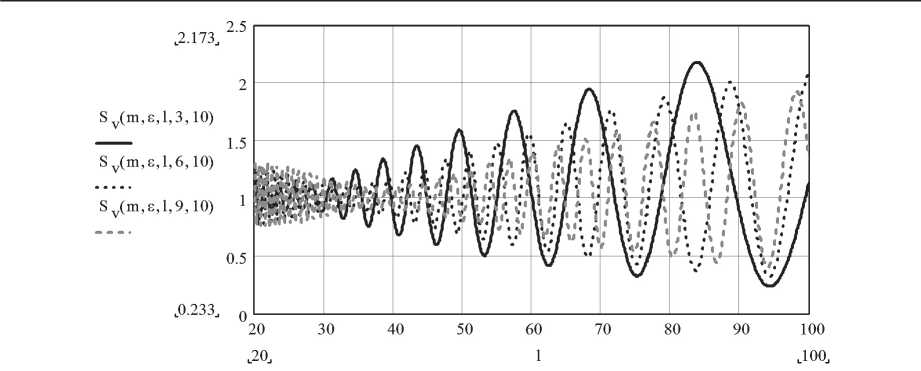
Рис. 2. Зависимость модуля ослабления суммарной волны с вертикальной поляризацией от удаления антенн при различных значениях высоты подъема антенны БС

В зависимости от высоты антенны БС h₁ изменяется частота колебаний.

Чем выше антенна БС, тем больше частота, а с увеличением расстояния между антеннами частота колебаний уменьшается. Расчеты показали, что при изменении m и ε колебания множителя ослабления изменяются лишь по амплитуде.

На рис. 3 показана зависимость модуля ослабления суммарной волны с горизонтальной поляризацией от удаления антенн при различных значениях высоты подъема антенны.

В данном случае амплитуда колебаний модуля множителя ослабления по мощности суммарной волны постоянно возрастает.

В общем случае поляризация волны неизвестна, потому что при отражении поляризация изменяется, а ориентация антенны АРБ случайна.

Зависимость квадрата модуля множителя ослабления при произвольной поляризации найдем из выражения

Sv ( m, e , l, h₁, h₂ ξ ) =

= 7 ( S v (m , s , l,h i ,h 2 )cos ( f ) ) 2 + ( S v (m, s , l,h i ,h 2 )sin ( f ) ) 2

На рис. 4 показана зависимость модуля ослабления при различном угле поляризации волны.

Как видно из рис. 4, от угла поляризации зависит только амплитуда множителя ослабления.

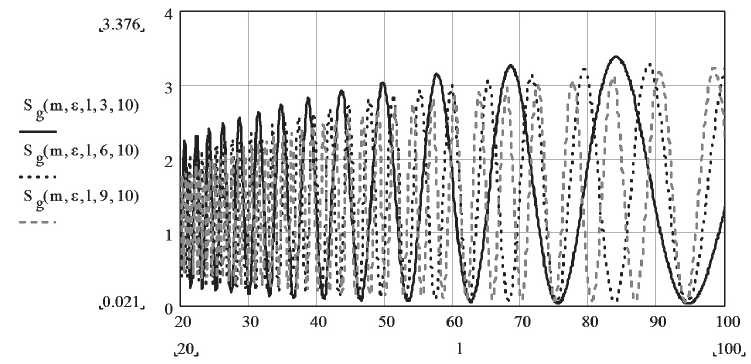
Рис. 3. Зависимость модуля ослабления суммарной волны с горизонтальной поляризацией от удаления антенн при различных значениях высоты подъема антенны

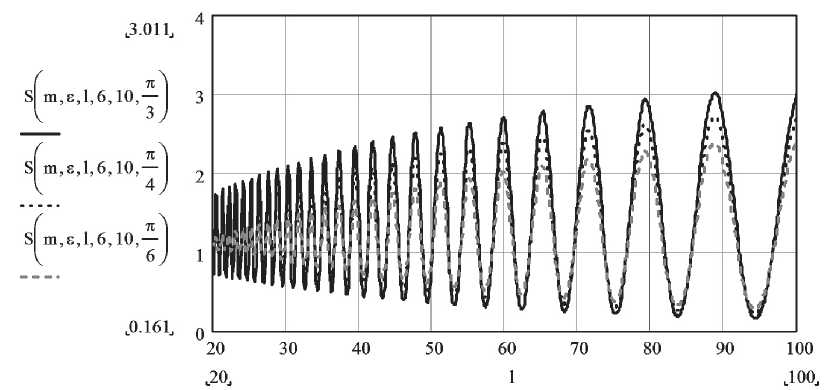
Рис. 4. Зависимость модуля ослабления суммарной волны от удаления антенн при различном угле поляризации волны и различных значениях высоты подъема антенны

Таким образом, исследования показали, что мощность суммарной волны на входе приемного устройства носит колебательный характер, частота зависит от высот подъема антенн и их удаления, а амплитуда — от поляризации волны и от свойств отражающей поверхности.

Расположение антенны БС внутри зданий

Рассмотрим среду распространения радиоволн внутри здания, где сигнал от антенны БС, располагающейся в помещении, претерпевает отражения как от пола, так и от потолка.

Геометрические соотношения для данной ситуации показана на рис. 5, где Н — высота потолка; h₁ — высота подвеса антенны БС; h₂ — высота подвеса антенны АРБ; l — разнесение антенн; r₁ — путь прямого распространения; r₂ — путь распространения при отражении от пола; r₃ — путь распространения при отражении от потолка.

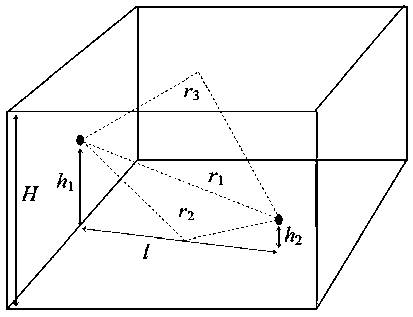
Рис. 5. Распространение волн внутри здания (трехлучевая аппроксимация)

Воспользовавшись геометрическими соотношениями, можно записать следующие выражения для разностей длин путей распространения волн между прямым и отраженными лучами r1= (h2-h1)2+l2

r2 = ^ (h1 + h2 )2 + l2

r3 = (2H - h1 - h2)2 + l2

Разность хода отраженных лучей и прямого луча можно записать как

Δr2 = r2 — r1(12),

Δr3 = r3 — r1(13),

Результирующая напряженность поля в точке приема Е^· складывается из напряженности прямой волны Е^·_пр , напряженности отраженной от пола волны Е^· и от потолка Е^· отр2                     отр3

Е^· С = Е^· пр + Е^· отр2 + Е^· отр3                         (14).

Записав по аналогии с (3), (4) выражения для напряженностей прямой и отраженных волн, найдем напряженность суммарной волны и далее выражение для комплексного множителя ослабления в освещенной зоне

W ^& = 1 + ^{r 1} F ^& 2 exp ⎢^⎡- j ⎜^{⎛ 2} π ⎟^⎞Δ r 2 ⎥^⎤ r ₂       ⎣ ⎝ λ ⎠ ⎦

r ⎡ ⎛ 2 π ⎞  ⎤

+ _r ¹ F 3 exp ⎢_⎣- j ⎜_⎝^⎛ _λ ⎟_⎠^⎞Δ r 3 ⎥_⎦    (15).

В рассматриваемом случае комплексные коэффициенты отражения находятся для диэлектрика для горизонтальной и вертикальной поляризации по формулам [1].

Для расчета коэффициента отражения необходимо знать угол, под которым волна падает на отражающую плоскость. В соответствии с геометрическими соотношениями угол отражения от пола вычисляется как:

π ⎛ h + h

ϕ ₂ ( l , h ₁, h ₂ ) = ₂ - arctg ⎜_⎝ ¹ _l ²

(16),

а от потолка, соответственно, по формуле:

π      ⎛ 2 H - h - h ⎞

ϕ ₃ ( l , h ₁, h ₂ ) = ₂ - arctg ⎜_{⎝       l} ^{1    2} ⎟_⎠                    (17).

Квадрат модуля ослабления напряженности волны согласно (15) будет иметь вид

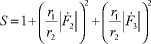
+ 2 _r ^{r 1} F ^& ₂ cos ⎢_⎣^⎡⎜^{⎛ 2} _λπ ⎟_⎠^⎞Δ r ₂ + arg F ^& ₂ ⎥_⎦^⎤+

■

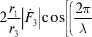
Δ r ₃ + arg F ₃ ⎥_⎥+

+ 2 ^r 1² F & 2 F & 3 cos ⎢^⎡⎜^{⎛ 2 π} ⎟^⎞ ( Δ r 2 r ₂ r ₃           ⎣⎝ λ ⎠

- Δ r ₃ ) + arg F ^& ₂ - arg F ^& ₃

(18),

На рис. 6 показана зависимость модуля ослабления суммарной волны с вертикальной поляризацией S_v ( ε , l, h₁, h₂) от удаления антенн при различных значениях высоты подъема антенны БС для помещения с высотой потолка H = 3 м.

Из рисунка видно, что график множителя ослабления существенно зависит от высоты подъема антенны. При высотах h ₁ = 1 м и h ₁ = 2 м графики совпадают, так как при высоте потолка H = 3 м длина пути отраженной волны от пола (при h ₁ = 1 м) становится равной длине пути отраженной волны от потолка ( h ₁ =

2 м) и наоборот. При закреплении антенны БС у потолка или около пола присутствуют только две волны, которые из-за разности путей распространения, как видно из графика, почти компенсируют друг друга.

Существует также такое положение антенны БС, при котором отраженные волны при заданной высоте АРБ проходят одинаковое расстояние и складываются в фазе.

На графике при высоте потолка H = 3 м и высоте АРБ 1,5 м данному случаю соответствует кривая при высоте антенны БС 1,5 м.

Зависимость модуля ослабления суммарной волны с горизонтальной поляризацией от удаления антенн при различных значениях высоты подъема антенны БС для помещения с высотой потолка H = 3 м показана на рис. 7.

В данном случае наблюдаются те же закономерности при распространении радиоволн в помещении, как для случая волны с вертикальной поляризацией. Отличие заключается лишь в величинах напряженности полей.

В общем случае поляризация волны неизвестна. Выражение для квадрата модуля множителя ослабления при произвольной поляризации будет иметь вид:

S_v ( ε , l, h₁, h₂, ξ ) =

= ( S v ( ε , l , h 1 , h 2 )cos( ξ ) ) ² + ( S v ( ε , l , h 1 , h 2 )sin( ξ ) ) ²(19),

На рис. 8 показана зависимость модуля ослабления S_v ( ε , l, h₁, h₂, ξ ) при различном угле поляризации волны.

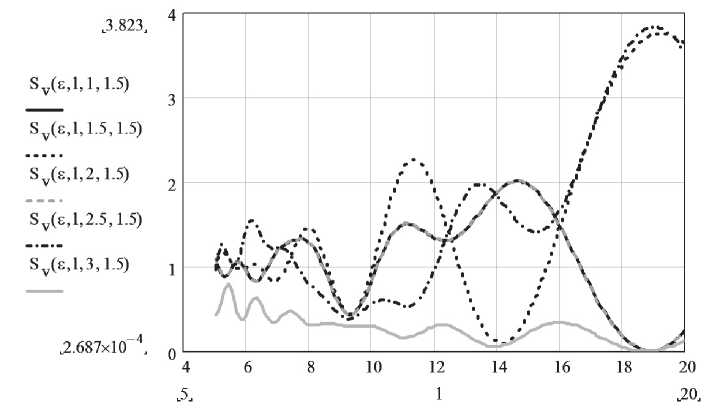
Рис. 6. Зависимость модуля ослабления суммарной волны с вертикальной поляризацией от удаления антенн при различных значениях высоты подъема антенны БС для помещения с высотой потолка H = 3 м

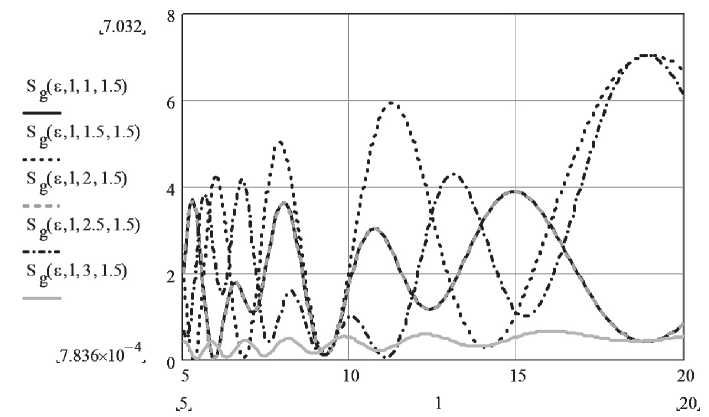
Рис. 7. Зависимость модуля ослабления суммарной волны с горизонтальной поляризацией от удаления антенн при различных значениях высоты подъема антенны БС для помещения с высотой потолка H = 3 м

Для случая двух лучей при трех лучах от угла поляризации зависит только амплитуда множителя ослабления.

При распространении волны в помещении отражение происходит не только от пола и потолка, но и от стен и других предметов. Отражение от различных предметов, находящихся в помещении, очень трудно поддается прогнозу, особенно тогда, когда абонент перемещается. Однако если учесть небольшие раз- меры предметов по сравнению с дальностью связи, то вероятность попадания отраженного от предметов луча на антенну АРБ очень мала, поэтому данными лучами можно пренебречь и учесть только отражения от стен. Таким образом, необходимо найти сумму напряженности прямой волны, отраженных от пола, потолка и двух стен.

Геометрические соотношения рассматриваемого случая показаны на рис. 9, где H — вы-

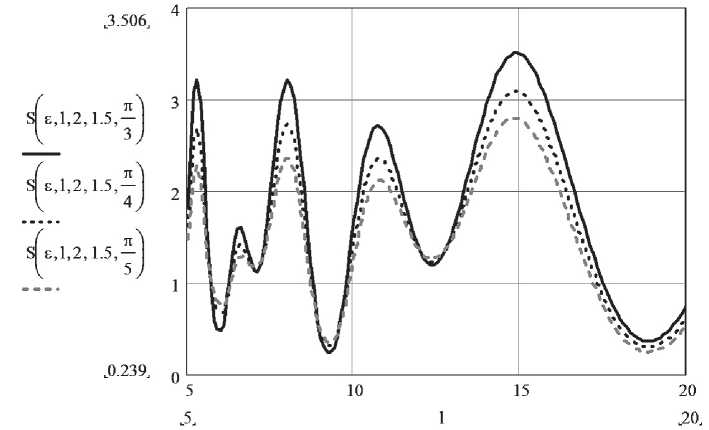
Рис. 8. Зависимость модуля ослабления суммарной волны с произвольной поляризацией от удаления антенн при различных значениях угла поляризации ξ для помещения с высотой потолка H = 3 м

сота помещения, K — ширина помещения, h₁ — высота антенны БС, h₂ — высота антенны АРБ, k₁ — расстояние от боковой стены до БС, k₂ — расстояние от боковой стены до АРБ, l² — расстояние от стены, на которой расположена БС, до АРБ, l — расстояние между БС и АРБ, r₁ — прямой путь распространения, r₂ — путь распространения волны, отраженной от пола, r₃ — путь распространения волны, отраженной от потолка, r₄ — путь распространения волны, отраженной от задней стены, r₅ — путь распространения волны, отраженной от передней стены.

женности прямой волны (Е·пр), напряженности волны отраженной от пола (Е·отр2), от потолка (Е·отр3), от задней стены (Е·отр4) и передней стены (Е· р )                          р отр5·        ·          ·             ·             ·             ·

Е_С= Е_пр+ Е_отр2+ Е_отр3+ Е_отр4+ Е_отр5         (31).

Записав по аналогии с (2), (3) выражения для напряженности прямой и отраженных волн, найдем напряженность суммарной волны и далее выражение для комплексного множителя ослабления в освещенной зоне

W ^& = 1 + _r ^{r 1} F ^& ₂ exp ⎢_⎣^⎡- j ⎜_⎝^{⎛ 2} _λ π ⎟_⎠^⎞Δ r ₂ ⎥_⎦^⎤ + _r ^{r 1} F ^& ₃ exp ⎢_⎣^⎡- j ⎜_⎝^{⎛ 2} _λπ ⎟_⎠^⎞Δ r ₃ ⎥_⎦^⎤+

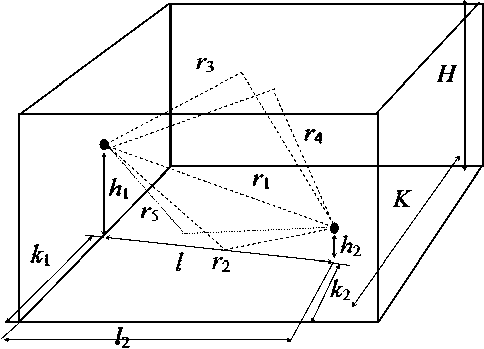
Рис. 9. Распространение волн внутри здания (пятилучевая аппроксимация)

Исходя из сделанных обозначений, запишем выражения для вычисления путей распространения радиоволн по различным путям:

l = (k1 - k2 )2 + l22

r1 = (h1 -h2)2 +l22

r2 = (h1 + h2 )2 + l22

r3 = (2H -h1 -h2)2 +l22

k = (h1 - h2 )2 + l22

r4 = (2K -k1 -k2)2 + k(25);

r5 = (k1 + k2 )2 + k(26).

Обозначим разности хода отраженных лучей и прямого луча, запишем как

Δr2 = r2 — r1(27);

Δr3 = r3 — r1(28);

Δr4 = r4 — r1(29);

Δr5 = r5 — r1(30).

Результирующая напряженность поля в точке приема ( Е^· ) складывается из напря-

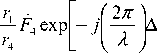
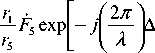
В рассматриваемом случае, так же как и в предыдущем, комплексные коэффициенты отражения также находятся для диэлектрика для горизонтальной и вертикальной поляризации и по формулам [1].

В соответствии с геометрическими соотношениями, показанными на рис. 9, углы падения волн на потолок, пол и стены вычисляются по формулам

ϕ 2 ( l 1 , l 2 , k 2 , h 1 , h 2 ) =

π ⎛ h + h ⎞ ₂ - arctg ⎜_⎝^{⎛ 1} _l ² ⎟_⎠^⎞

ϕ 3 ( l 1 , l 2 , k 2 , h 1 , h 2 ) = π ₂ -

ϕ ₄ ( l ₁, l ₂, k ₂, h ₁, h ₂ ) = π ₂ -

ϕ ₅ ( l ₁, l ₂, k ₂, h ₁, h ₂ ) = π ₂ - arctg ⎜

(33);

2 H - h ₁ + h ₂ l

2 K - h ₁ - h ₂

l

(34);

(35);

(36);

Квадрат модуля ослабления напряженности волны согласно (23) будет иметь вид

S = 1 +

+ 2 ^{r 1}

г *

r ₂

r ₁

r ₃

⎟ +

I

Δ r ₂ + arg F ₂

I

Δ r ₃ + arg F ₃

+

+

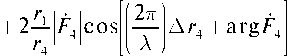
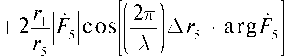
+ 2 _{r 2 r 3} F & 2 F & 3 cos ⎢_⎣^⎡⎜_⎝^{⎛ 2} _λ π ⎟_⎠^⎞ ( Δ r 2

- Δ r ₃ ) + arg F ^& ₂ - arg F ^& ₃ ⎥^⎤ +

+ 2 _{r 2 r 4} F & 2 F & 4 cos ⎢_⎣^⎡⎜_⎝^{⎛ 2} _λ π ⎟_⎠^⎞ ( Δ r 2

- Δ r ₄ ) + arg F ^& ₂ - arg F ^& ₄ ⎥^⎤ +

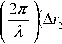
- Δ r ₅ ) + arg F ^& ₂ - arg F ^& ₅

+ 2 ^{r 1} - F 2 F 5 cos _⎢ r ₂ r ₅

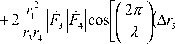
-Δ r ₄ ) + arg F ^& ₃ - arg F ^& ₄ ⎥^⎤+

- Δ r ₅ ) + arg F ^& ₃ - arg F ^& ₅ ⎥ +

+

+ 2 ^{r 1}₇| F ^& 4 F ^& 5 cos ⎢^⎡⎜^{⎛ 2} π ⎟^⎞ ( Δ r ₄ -Δ r ₅ ) + arg F ^& ₄ - arg F ^& ₅ ⎥^⎤ (37).

r ₄ r ₅ ⎣⎝ λ ⎠ ⎦

На рис. 10 показана зависимость квадрата модуля ослабления суммарной волны с вертикальной поляризацией S_v (m, ε , h₁, h₂, k₁, k₂, l₂) от удаления антенны АРБ от антенны БС по стене ( l ₂) при различных значениях удаления от стены антенны АРБ ( k ₂) для помещения с высотой потолка H = 3 м.

Как видно из графика, при смещении АРБ от стены квадрат модуля множителя ослабления также изменяется, потому что изменяются расстояния прохождения отраженных от стены радиоволн.

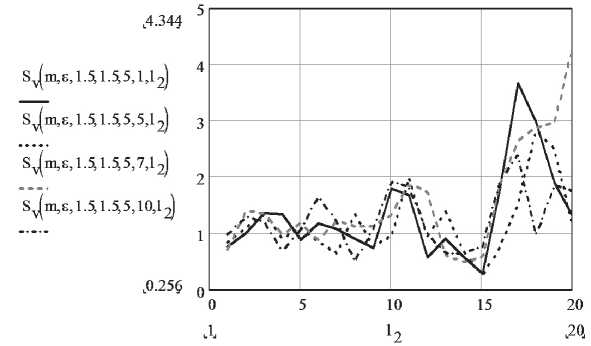
Рис. 10. Зависимость квадрата модуля ослабления суммарной волны с вертикальной поляризацией от удаления антенны АРБ от антенны БС по стене (l₂) при различных значениях удаления от стены антенны АРБ (k₂) для помещения с высотой потолка H = 3 м

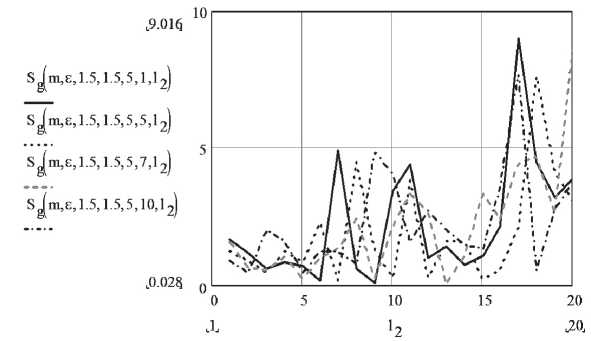
Рис. 11. Зависимость квадрата модуля ослабления суммарной волны с горизонтальной поляризацией от удаления антенны АРБ от антенны БС по стене (l2) при различных значениях удаления от стены антенны АРБ (k2) для помещения с высотой потолка H = 3 м

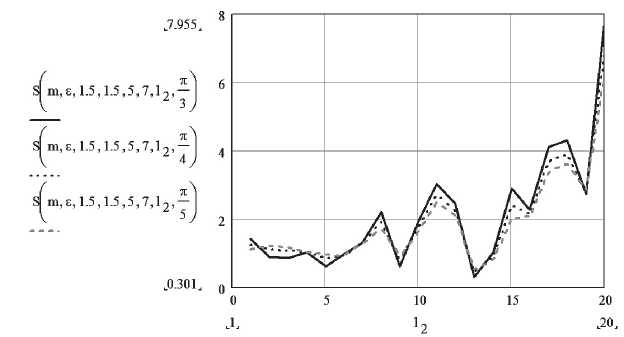
Рис. 12. Зависимость квадрата модуля ослабления суммарной волны с произвольной поляризацией от удаления антенны АРБ от антенны БС по стене (l2) при различных значениях угла поляризации ( ξ ) для помещения с высотой потолка H = 3 м

На рис. 11 показана зависимость квадрата модуля ослабления суммарной волны с горизонтальной поляризацией Sg ( m, e , h₁, h₂, k₁, k₂, l₂) от удаления антенны АРБ от антенны БС по стене ( l ₂) при различных значениях удаления от стены антенны АРБ ( k ₂) для помещения с высотой H = 3 м.

На рис. 12 показана зависимость квадрата модуля ослабления суммарной волны с произвольной поляризацией S ( m, e , h₁, h₂, k₁, k₂, l₂, x ) от удаления антенны АРБ от антенны БС по стене ( l ² ) при различных значениях угла поляризации ( ξ ) для помещения с высотой потолка H = 3 м.

Как видно из графика, квадрат модуля множителя ослабления незначительно изменяется от угла поляризации. Поэтому так же, как в предыдущих случаях можно в дальнейшем рассматривать неполяризованную волну.

Таким образом, получены выражения для нахождения напряженности поля на входе приемника в условиях многолучевого распространения радиоволн при размещении БС вне здания и внутри помещения. Результаты расчетов по данным формулам показывают, что характер колебания напря жен-ности существенно зависит от расположения БС и АРБ, в то же время поляризация волны сказывается лишь на амплитуде колебаний.