Влияние модели химической кинетики на результаты численного моделирования турбулентных течений с горением

Наиболее надежным способом описания турбулентного течения с горением была, бы процедура, при которой сначала, по локальным параметрам течения вычислялись бы скорости образования веществ на основе механизма химической реакции, а потом с учетом полученных скоростей в малой области пространства, и времени, где эти скорости применимы, решались бы напрямую мгновенные (не осредненные по времени) уравнения движения газа. В этом смысле механизм химических реакций горения, связывающий микроскопические и макроскопические явления горения, является основой для численного моделирования и понимания природы горения. К сожалению, одновременное протекание многочисленных химических процессов и турбулентные пульсации в каналах с пограничными

«Московский физико-технический институт (национальный исследовательский университет)», 2023

слоями создают настолько широкий диапазон масштабов физических процессов, что непосредственная реализация указанного способа (прямое численное моделирование) остается недостижимой для сколько-нибудь реальных постановок задачи. Поэтому для решения практических задач необходимо корректное упрощение задачи, сохраняющее важнейшие физические процессы, протекающие в потоке. Как правило, такие упрощения связаны с сокращением числа химических реакций и компонент реагирующей смеси, с осреднением уравнений движения газа по времени (уравнения Рейнольдса, RANS) или по пространству (моделирование крупных вихрей, LES). При этих упрощениях возникает необходимость в дополнительных математических моделях, замыкающих систему уравнений движения газа: 1) в модели химической кинетики, которая приближенно описывает вклад всех реакций и всех компонент, которые не учитываются в расчете; 2) в модели турбулентности, которая приближенно описывает вклад тех турбулентных движений, которые не описываются расчетом; 3)в модели турбулентного горения (TCI - turbulence-combustion interaction), которая приближенно описывает влияние турбулентных пульсаций на средние скорости реакций и влияние тепловыделения при горении на турбулентный перенос.

В наиболее универсальной формулировке для описания течения газа с горением к системе уравнений движения добавляются дифференциальные уравнения в частных производных для массовых или мольных долей каждого химического вещества в изучаемой системе. Эти связанные уравнения часто порождают широкий спектр сильно различающихся характерных временных масштабов, что приводит к «жесткости» (существенному влиянию быстро затухающих мод на устойчивость решения). Стандартные методы решения дифференциальных уравнений, как правило, неэффективны при решении жестких систем [1]. Началу развития химических кинетических механизмов способствовала разработка решателей жестких систем кинетических уравнений. Первыми моделируемыми химическими системами были системы, описывающие озон [2] и разложение гидразина [3], за которыми последовали модели, описывающие горение водорода [4], метана [5, 6] и метанола [7, 8].

По количеству компонентов и реакций модели химической кинетики можно условно разделиться на четыре категории: детальные, скелетные, редуцированные и глобальные. В первых могут быть сотни реакций и компонент. В последних - одна или несколько реакций и несколько компонент. Первые и вторые допускают разные сценарии развития реакции; третьи и четвертые, как правило, настроены на воспроизведение какого-либо одного сценария. Чем меньше реакций и компонент, тем модель менее универсальна и менее надежна.

Последовательность химических процессов в потоке определяет локализацию зон тепловыделения и играет существенную роль в формировании газодинамической структуры течения и практически значимых характеристик энергетических устройств. Вычислитель должен представлять возможные последствия выбора того или иного кинетического механизма и уметь анализировать влияние кинетической модели на физические процессы, протекающие в потоке. Исследования данного влияния ведутся постоянно наряду с развитием технологий компьютерного моделирования.

В 80-х годах XX в. исследование высокоскоростных течений с горением основывалось на уравнениях квазиодномерного течения в стационарном приближении. В работе [9] сопоставлено влияние модели химической кинетики с 8 реакциями и с 25 реакциями на результаты расчетов круглой сверхзвуковой струи водорода в спутном сверхзвуковом потоке воздуха и выдува плоской пристенной струи водорода в спутный сверхзвуковой поток воздуха из щели в стенке аэродинамической трубы. В работах [10, 11] изучалось влияние неопределенности коэффициентов скоростей реакций на вычисленные времена задержки воспламенения, скорости горения и характеристики камеры сгорания. Позже в работе [12] были рассмотрены и сопоставлены три кинетики для описания процесса воспламенения неперемешанной системы водород/воздух в сверхзвуковом слое смешения с температурами более 1000 К.

В работе [13] на базе осреднённых по Рейнольдсу уравнений Навье - Стокса (RANS) исследовано влияние модели химической кинетики на моделирование поднятого сверхзву- нового пламени. Также в работе [14] было исследовано влияние модели химической кинетики на распределение компонентов в пристеночном сверхзвуковом горении водорода в воздухе. В последнее десятилетие болвшое внимание привлекло сочетание метода крупных вихрей (LES) с химическими кинетическими моделями и моделью турбулентного горения. Влияние кинетики было исследовано в высокоскоростной водородно-воздушной камере сгорания с пилонами [15-17]. Канал с обратным уступом является классической конфигурацией для стабилизации горения, особенно для высокоскоростного потока. Влияние кинетики на процесс стабилизации горения углеводородного топлива и на колебательные процессы в плоском канале со ступенькой были изучены в работах [18-19].

В данной статье на примере численного моделирования двух классических экспериментов анализируется влияние модели химической кинетики на структуру и характеристики течения, получаемые при расчете данных классов течений. Первый эксперимент касается высокоскоростного неперемешанного горения водорода со стабилизацией за счет самовоспламенения, а второй - медленного предварительно перемешанного горения метана со стабилизацией на ступеньке и возникновением волны диффузионного пламени. Такие противоположные постановки задачи выбраны для того, чтобы максимально расширить область применимости сделанных в работе выводов.

2.    Модели и численные методы

В расчетах решались нестационарные осреднённые по Рейнольдсу уравнения Навье -Стокса (URANS - Unsteady RANS) для реагирующего многокомпонентного сжимаемого газа:

др + дри3 = 0 дt дхз"

Әри^ + Ә р и) = - dp_ + Ә dt дх3         дхг    dxj 1313

дрЕ   д (pujE)     д (puj)

”эҒ+   дх = X    дХ и (Тіз+ р^)+ qj+ p°j+ ^j (^)+ Jij ] ’ дрҮк , др^Үк = -ЭУз (Үк) , _ дt      дхз          дхз где t - время: Xj(j = 1,2,3) - декартовы

N ты вектора скорости: p = pRoТ Е PT к=1  "

координаты: р - плотность: Uj - компонеіі-

давлеіше: Ү_к - массивая доля к-го компо-

нента смеси; R q ~ 8.314 ^,_к - универсальная ра: т к - молекулярный вес к-го компонента: Е

газовая постоянная; Т - температу-

UmUm

+ ^к + Ln • ф (^Т) - ^^Т)

- полная энергия единицы массы; к = булентности; һ к = Дһд к + !т₀ с_Р ,к (Т ‘ )^Т ‘

^ ‘‘  ‘‘

P-U-m-U-m

2Р

средняя кинетическая энергия тур-

- энтальпия единицы массы к-го компонен-

та, включающая Дһ^ к ^- энтальпию образования вещества при стандартной температуре Тд; с_р ,к (Т ) - теплоемкость единицы массы к-го компонента при постоянном давлении; T ij = p д^-^ + ру х — з Р дР ^^ ij^ ^- тензор молекулярных потоков импульса (вязких напряжений); р(Т ) - молекулярная вязкость, которая принимается равной вязкости воздуха;

“ ‘‘ ‘‘               8u;   , ди,- pRгj = - риг Uj ^ 2pt^ + дуЗ-

-

3 дЕ ^^ ij^ - 3 рк^ гЗ ~ тензор турбулентных потоков им-

пульса: p_t ~ турбулептііая вязкость: q j

-

^ И ~ молекулярный по ток тепла вдоль оси Xj.

связанный с градиентами температуры; ро^

-

TN7 И ~ аналогичный турбулентный по-

ток тепла; с_р = Е Ү к с_р ,к (Т ) - теплоемкость смеси; J j (Ү к ) ~ — (   +      дь һ ~ суммарный

к

(молекулярный и турбулентный) диффузионный поток массы к-го компонента вдоль оси

N х j\ Qj (Yb) = 52 ^fe (T) J j (Y^) - суммарный (молекулярный и турбулентный) поток тепла к=1

вдоль оси Xj, связанный с неоднородностью состава смеси; S^ = —т^^ур,,.Wt - хими-т ческий источник, описывающий скорость производства или расходования к-го компонента смеси за счет протекающих химических реакций (v^t - коэффициент при к-м веществе в уравнении г-н реакции. Wt = Wt (р + р,T + T", Y1 + Y1’’, ..., Yn + YN) ~ средняя скорость химической реакции. Черта сверху (осреднение по времени). Все параметры предполагаются осредненными в соответствии с правилами осреднения Фавра (плотность и давление осредняются по времени, остальные параметры - по формуле а = ра/р, где а - мгновенное значение); один штрих - пульсация при осреднении по времени (а' = а — а), два штриха

- пульсация при осреднении по Фавру (а'' = а — а). Знаки осреднения опускаются всю

ду, кроме мест, где они необходимы. В формулах используется правило суммирования по повторяющемуся пространственному индексу.

Для замыкания системы уравнений (1) необходимы три модели - турбулентности, химической кинетики и турбулентного горения.

Модель турбулентности нужна для вычисления турбулентных потоков импульса, теп ла и массы компонент смеси. В настоящей работе для этой цели используются модели класса к — ш, которые основаны на гипотезе Буссинеска. В этом случае для определения турбулентных потоков достаточно задать среднюю кинетическую энергию турбулентности к и турбулентную вязкость pt. В моделях класса к — ш турбулентная вязкость рассчитывается по формуле pt = рҒ^к/ш^ где ш - характерная частота турбулентных пульсаций скорости, а Ғ^ - функция, зависящая от фр - расстояния до ближайшей твердой стенки и равная 1 в свободной турбулентности. Для определения параметров киш ре шаются дополнительные дифференциальные уравнения в частных производных. В раз деле 3 используется модель турбулентности SST (Shear Stress Transport) [20], в которой Ғл = min [1 W]• S = 2 (д^ + Sf) (Й) + Ш ) - характерная величина, сдвиговой деформации, Ғ2 = tanh (arg2) , arg2 = max [0.029^w, І^;] • В разделе 4, кроме SST, используется модель BSL к — ш Ментера, описанная в той же работе [20]. В этой модели

Ғ_ц = 1.

Модель химической кинетики определяет набор компонент реагирующей смеси и вы ражения, определяющие мгновенные значения скоростей каждой химической реакции (т.е.

зависимости

W t

(P^,T,Y 1 , .-, ^Y n)

. В разделе 3 используются различные модели горения

водорода, в воздухе, в разделе 4 - различные модели горения метана, в воздухе.

Модель TCI (модель турбулентного горения) описывает два канала взаимодействия турбулентности с горением: 1-й канал - влияние турбулентных пульсаций на. средние скорости химических реакций (т.е. способ вычисления величины

Модели класса PaSR предполагают, что горение происходит только в части турбулентной области течения - в т.н. «тонких структурах», которые рассматриваются как реакторы, обменивающиеся массой и теплом с окружающей средой за счет диффузии. Наиболее известными моделями этого класса являются Eddy Dissipation Concept (EDC) Магнуссена [23] и модель PaSR Хомяка и Карлссона [24]. Эти модели основаны на допущении, что время реакции в тонких структурах гораздо меньше, чем характерное время среднего течения. Поэтому состояние в тонких структурах является квазистационарным и описывается алгебраической системой уравнений:

* 0

р* ^----^к = W_r (р*, Т *, Y1*

YV),

£ Y_k*h_k (Т *) = £ Y 0 һ_к (Т 0 ), < к=1               к=1

где звездочкой обозначены параметры газа в «тонких структурах», а индексом «0» - параметры газа в окружающем пространстве, где горения нет. Величина р*/т* представляет собой расход массы через единицу объема «тонких структур», а т* можно интерпретировать как характерное время пребывания газа в «тонких структурах». Физически обмен массой и энергией между «тонкими структурами» и окружающим пространством осуществляется за счет диффузии. Средние по времени параметры в данной области пространства, содержащей «тонкие структуры» с горением и окружающее пространство без горения, определяются соотношениями р = 7*р* + (1 - 7*)Р0, pYk = 7 *P*Y* + (1 -7 *)P0Y0,

р ]Г Yk һ к (Т ) = 7 *р* ҮҮ*ЫТ *) + (1 - 7 *)р⁰ Х^Л. (Т 0 ), к=1                 к=1                        к=1

где 7* - объемная доля тонких структур. Для замыкания системы уравнений (2) - (3) требуется еще дополнительное предположение относительно давления или плотности газа в тонких структурах. Поскольку скорость газа и в «тонких структурах», и в окружающем пространстве принимается в моделях PaSR равной средней скорости потока, естественным является допущение р* = р⁰ = р. Однако в настоящей работе, как и в [25], для упрощения выкладок используется гипотеза

р* = р⁰ = р. (5)

Система уравнений (3) - (5) является замкнутой системой алгебраических уравнений, которая при заданных параметрах т * и 7* позволяет выразить параметры газа в «тонких структурах» и в окружающем пространстве через параметры среднего течения (р, Т, Y1, ..., Yv). Как только параметры в «тонких структурах» найдены, средние скорости химических реакций определятся по формуле

* 0               *

W «7Ж + (1   ■■ W = 7*W_r (р ,Т *,Y* , ..., Y V )=7*р* ^к _т * ^к =7 *р ₍₁-₇ * ₎Т * . (⁶)

Недостатком моделей PaSR, основанных на уравнениях (3), является отсутствие учета переноса «тонких структур» по пространству за счет конвекции и диффузии. Этот недостаток устранен в модели EPaSR (Extended PaSR) Сабельникова и Фюрби [26], где вместо (3) решаются дополнительные уравнения в частных производных для параметров газа в тонких структурах и для объемной доли тонких структур 7*. Для достижения наилучшего решения задачи, которая рассмотрена в разделе 4 настоящей статьи, в работе ONERA [25], а позднее в работах ЦАРИ [22, 27] была применена именно модель EPaSR.

Формула квазиламинарного приближения (2) или приближения PaSR (5) вместе с моделями турбулентности и химической кинетики завершает замыкание системы уравнений движения газа (1).

Все представленные в статье расчеты выполнены автором при помощи коммерческого пакета вычислительной аэродинамики ANSYS Fluent [28]. Использовался неявный конечнообъемный численный метод 2-го порядка аппроксимации по всем переменным, включающий противопоточную схему для конвективных потоков, центрально-разностную для диффузионных потоков и устойчивую локально-неявную аппроксимацию жестких химических Источниковых членов. Для интегрирования по времени использовалась неявная схема 1-го порядка точности по физическому времени с дуальным шагом по времени.

Как показано в работе автора [29], в задаче, которая рассмотрена в разделе 3, вклад молекулярной диффузии мал по сравнению с турбулентной, поэтому для описания молекулярной диффузии молекулярная вязкость и коэффициенты молекулярной диффузии тепла и массы принимались равными своим значениям для воздуха. Вязкость ^(Т ) рассчитывалась по формуле Сазерленда, а молекулярные числа Прандтля и Шмидта полагались равными Pr = 0.72, Sс = 0.9.

В ANSYS Fluent из моделей турбулентного горения класса PaSR доступны только различные варианты модели EDC Магнуссена. Чтобы максимально приблизиться к рекомендациям работы [22], автор разработал плагин (UDF) для ANSYS Fluent, превращающий модель EDC в модель PaSR Хомяка и Карлссона [24], наиболее близкую к модели EPaSR.

3/4    .

, где е - средняя скорость

В модели EDC Магнуссена [23] у* = 9.7( -^2)   , т *

диссипации кинетической энергии турбулентности. В моделях турбулентности класса к — ш скорость диссипации рассчитывается по формуле е = 0.09кш. В модели PaSR Хомяка и Карлссона [24], которая используется в разделе 4 настоящей работы,

- * у

T ch

T ch + T * ,

т *=сщОЕ,

^гД^е T_c h ^ характерный масштаб времени химических процессов в «тонких структурах». Вопрос об определении параметра т_с һ и эмпирического коэффициента С_т будет рассмотрен в разделе 4 настоящей статьи.

3.    Влияние кинетики на результат расчета высокоскоростного течения с горением в расширяющим канале

Вначале рассмотрим эксперимент, в котором было детально исследовано высокоскоростное неперемешанное горение водорода в воздухе со стабилизацией преимущественно за счет самовоспламенения. Такая серия экспериментов была поставлена во Французской аэрокосмической Лаборатории (ONERA) в рамках европейского проекта LAPCAT-II, см. [30]. Эксперименты проводились в режиме присоединенного воздуховода на стенде ONERA LAERTE (рис. 1). Входное сечение сопла Лаваля пристыковано к огневому подогревателю воздуха длиной 0.254 м, в котором для достижения высокой температуры торможения осуществляется сжигание водорода с последующим обогащением потока кислородом. Экспериментальная модель LAPCAT-II представляет собой расширяющийся канал прямоугольного сечения постоянной боковой ширины 0.04 м, длиной 1.192 м, с подачей топлива со стенок перпендикулярно потоку и с оптическими окнами по всей длине канала, что позволило визуализировать структуру течения методами высокоскоростной шлирен-видеосъемки и зарегистрировать хемилюминесценцию возбужденных радикалов ОН*. Детали геометрии приведены в [30].

На стенде были проведены эксперименты при различных условиях работы. Для данного численного исследования был выбран один из них, соответствующий «Case В» в статье [31]. В этом режиме наблюдалось сверхзвуковое горение, индуцированное ударными волнами.

Результаты моделирования течения в подогревателе и сопле Лаваля можно найти в статье с участием автора [32]. В работе [32] было показано, что для получения состава в конце сопла Лаваля расчет подогревателя и сопла должен быть выполнен с учетом реакций с пероксидами НО2 и Н2О2.

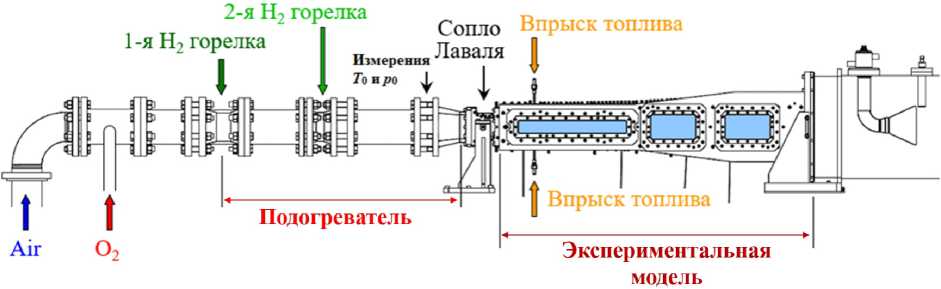
Рис. 1. Общий вид установки LAERTE (ONERA - Palaiseau Center)

Полученные в расчетах подогревателя поля течения на входе в экспериментальную модель ONERA использовались в качестве входного граничного условия во всех описанных ниже расчетах, независимо от используемой модели химической кинетики. В ядре потока на входе в канал модели число Маха М ~ 2, температура торможения Т о ~ 1705 К, давление торможения р о ~ 4.07 бар. Соотвстствуюппч? число Рейнольдса Неи ~ 165620 (посчитанное по высоте канала). Характерная толщина пограничных слоев во входном сечении канала 6/Н ~ 0.054. Расходы топлива и входящего в канал загрязненного воздуха соответствовали коэффициенту избытка топлива р = 0.153. В соответствии с рекомендациями [31], температура стенок канала в расчетах полагалась равной Тщ = 716 К.

На внутреннюю поверхность канала экспериментальной модели LAPCAT-II нанесено теплозащитное покрытие (оксиды циркония и иттрия). Поэтому для корректного описания течения в канале необходим учет шероховатости. Применялась модель шероховатости, предложенная в работе [33] на базе корреляции [34] для использования с моделями турбулентности класса к — ш, включая SST. В модели шероховатости [33] в качестве характерного размера шероховатости рекомендуется выбирать эквивалентный диаметр песчинки h_s. В работе [31] для расчетов течения в модели ONERA рекомендовано значение h_s = 65 мкм. Однако в работе автора [29] наиболее близкий к эксперименту результат был получен при h_s = 200 мкм. Согласно современной точке зрения [35], эквивалентный диаметр песчинки h_s можно рассматривать как настроечный параметр расчета, который должен обеспечить правильное распределение трения по стенкам канала. В настоящей работе использовалось значение h_s = 200 мкм.

Были рассмотрены две модели кинетики горения водорода, в воздухе: наиболее простая модель Яхимовского с 7 реакциями и 7 веществами (Н, О, ОН, Н2О, Н2, О2 и инертный N2), основанная на работе [36], и модель Яхимовского с 19 реакциями, выделенная из детального механизма [10], в которой к перечисленным 7 веществам добавлены еще пероксиды НО2 и Н2O2. Детали модели с 7 реакциями описаны в работе [29]. Рисунок 2 показывает, что обе кинетики дают похожие распределения давления по стенкам канала. Однако трехмерная структура течения, соответствующая этим распределениями давления, в расчетах с 7 и 19 реакциями оказалась разной.

На рис. 3 показаны поле десятичного логарифма, локальной скорости тепловыделения и поля числа. Маха, в плоскости симметрии канала. Видно, что тепловыделение в основном происходит в дозвуковой зоне за. струей, где водород хорошо смешивается с окислителем. При ж > 0.28 м за счет расширения канала скорость потока увеличивается, давление резко падает, и тепловыделение снижается. Сильное тепловыделение наблюдалось у стенки как в расчете с 7 реакциями и с 19 реакциями. Но вдали от стенки тепловыделение в расчете с

7 реакциями в основном сосредоточено в задней части дозвуковой зоны, а тепловыделение в расчете с 19 реакциями сосредоточено в передней части.

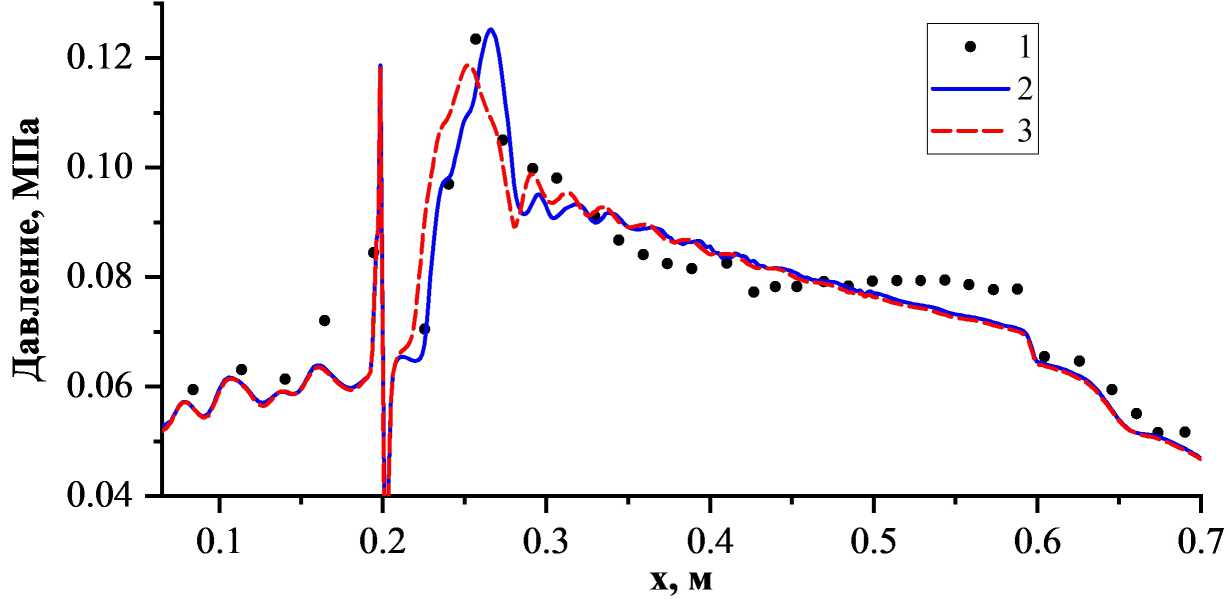
Рис. 2. Распределения статического давления по нижней стенке канала, (Ту = 716 К, h ₈ = 200 мкм): 1 - Эксперимент ONERA; 2-7 реакций; 3  19 реакций

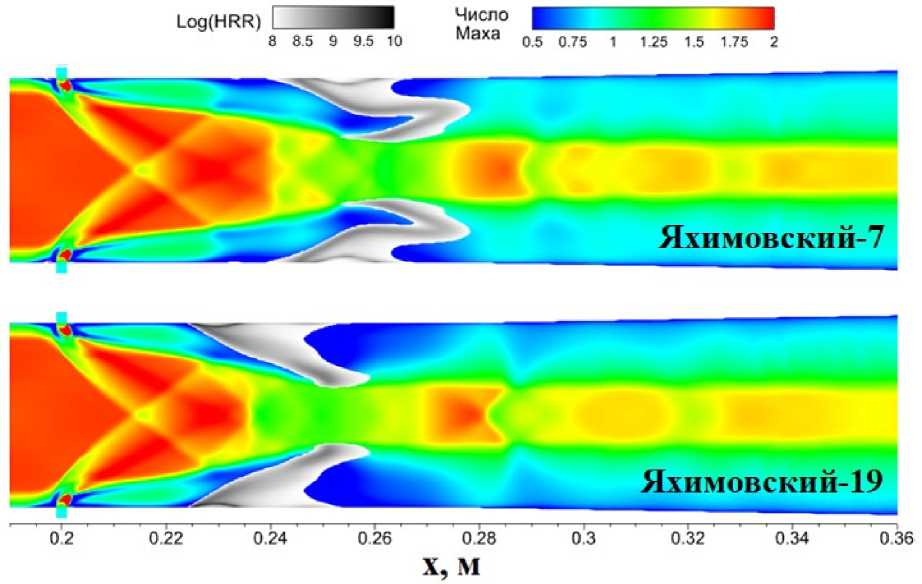
Рис. 3. Поле десятичного логарифма локальной скорости тепловыделения наложено на поле числа Маха в плоскости симметрии канала ( Т у = 716 К, h _s = 200 мкм)

На рис. 4а, б для моделей кинетики с 7 и с 19 реакциями представлены поля десятичного логарифма массовой доли радикала Н в серии поперечных сечений на участке ж = 0.197 ~ 0.28 м, а на рис. 4в - поле десятичного логарифма массовой доли пероксида НО2 (который учитывался только в расчете с 19 реакциями). Видно, что в расчете с 7 реакциями радикал Н начинает расти уже в отрывной зоне перед струей водорода и затем монотонно производится вплоть до области тепловыделения (ж = 0.24 ~ 0.28 м). Это типично для процесса самовоспламенения, определяемого ростом концентрации радикала Н. В расчете с 19 реакциями массовая доля радикала Н в окрестности струи водорода гораздо ниже; в следе за струей она не нарастает, а падает на участке ж = 0.197 ~ 0.21 м и начинает резко увеличиваться лишь в зоне тепловыделения (которая в расчете с 19 реакциями рас- положена на участке ж = 0.22 ~ 0.25 м). Следовательно, в этом расчете самовоспламенение смеси не связано с ростом радикала Н. Зато в этом расчете мы наблюдаем монотонный рост массовой доли пероксида НО2 на участке ж = 0.197 ~ 0.21 м и далее на участке интенсивного тепловыделения. Выделение тепла в реакции образования пероксида в сочетании с ростом давления и температуры в наклонном скачке уплотнения, порожденном струями водорода, вызывает самовоспламенение в этом расчете.

Почему тепловыделение в зоне отрыва перед струей в расчете с 7 реакциями на порядок больше, чем в расчете с 19 реакциями? На рис. 4 показаны поля массовой доли Н в плоскости симметрии канала в расчете с 7 реакциями и изолинии Ү н 2 = 0.1. В зоне отрыва перед струей химические реакции производились и большое количество Н образовалось. Процесс самовоспламенения газа быстрее, чем время его пребывания, является необходимым условием для протекания химической реакции в турбулентном течении. Поэтому были оценены время пребывания и время задержки воспламенения газа в разной модели кинетики в ядре зоны отрыва. Процесс самовоспламенения проводился в реакторе с постоянным давлением. Начальное условие получено в расчете с выключением реакций (табл. 1).

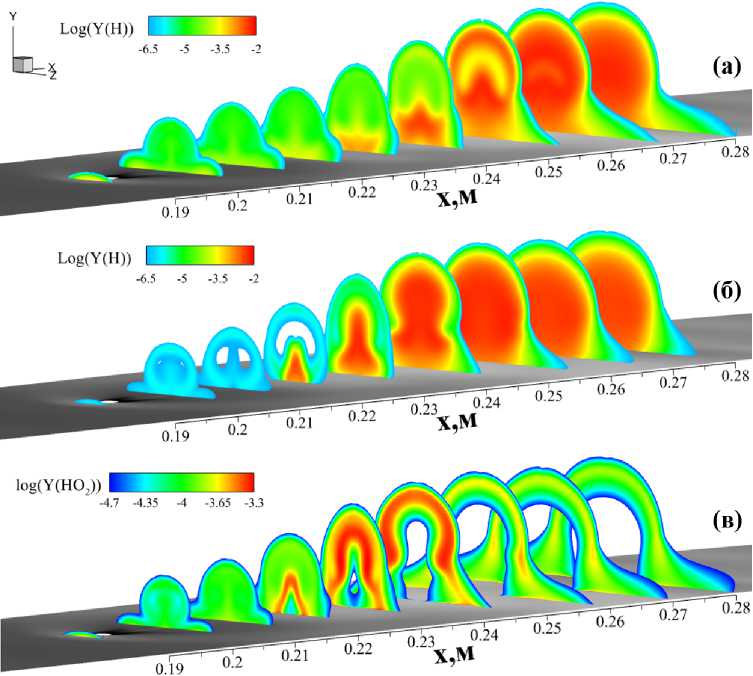
Рис. 4. Поля десятичного логарифма, массовой доли промежуточных веществ в поперечных сечениях на участке ж = 0.197 ~ 0.28 м: (а) - радикал Н, 7 реакций; (б) - радикал Н, 19 реакций;

(в) - НО 2. 19 реакций

Таблица. 1

Параметры в центре зоны рециркуляции перед струей в расчете с выключением реакций

	Һь	Ү 0 2	Ү н	Ү о	Ү он	Ү Н 2 О	р, Па	Т,К
Центр зоны отрыва	7.127е-3	0.2463	3.255е-7	3.054е-7	1.52е-4	0.1658	79387.02	1091.6

Оценки показывают, что характерное время, необходимое для увеличения массовой доли радикалов Н до величины 0.0002, составляет в расчете с 7 реакциями примерно 2 х 10^-5 с, а в расчете с 19 реакциями -8 х 10^-5 с. Характерное время пребывания газа внутри отрывной зоны (время одного оборота вихря в этой зоне) составляет т = L/V = 0.003/45 ~ 6.7 х 10^-5 с. С учетом неидеальности процесса в отрвівной зоне, этого времени достаточно для достижения TH = 0.0002 в расчете с 7 реакциями и недостаточно в расчете с 19 реакциями. Вот почему в расчете с 7 реакциями в зоне отрыва. перед струей реакция успевает пройти гораздо дал вше.

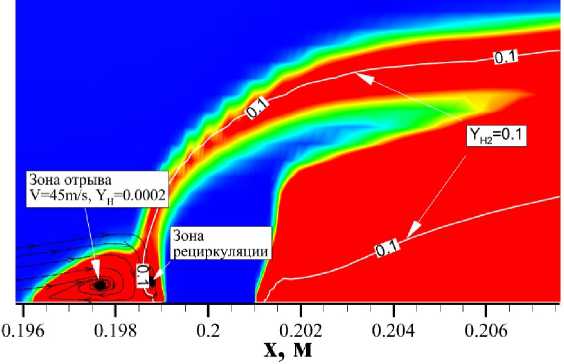
Рис. 5. Поле массовой доли Н в плоскости симметрии канала, в расчете с 7 реакциями. Показаны зона рециркуляции перед струей топлива и изолинии Үн 2 =0.1

Изменение структуры течения и тепловых потоков должно приводить к изменению тепловой полноты сгорания топлива, которая является важной тягово-экономической характеристикой течения в канале и может быть определена, следующей формулой [37]:

^{Q ( ж )} G_FH_U .

Здесь. Gf ~ полный расход топлива, втекающего в расчетную область. H_u - теплотворная способность топлива, Q (ж) - полное количество выделившейся теплоты, которое может быть получено следующим образом [37]:

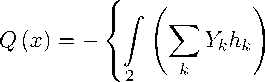
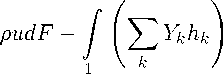
• pudF — G f Һ ғ * ,

где 1 - входное сечение канала (ж = 0.065 м), 2 - рассмотренное сечение канала, и -проекция скорости газа на ось ж. dF - элемент площади текущего поперечного сечения ж = const. Для реакции 2H2 + O2 ^ 2H2O в качестве теплотворной способности топлива с неплохой точностью можно взять значение при стандартной температуре Т = 293 К):

Hu

2rn H 2 ^h H 2 + m o 2 ^h O 2 ^— 2rn H 2 O ^h H 2 O 2ши 2

(Ю)

Результат оценки распределения полноты сгорания по длине канала показан в рис. 6. В расчетах течения с 7 реакциями полнота сгорания примерно на 5% ниже, чем в расчете течения 19 реакциями. Это расхождение связано прежде всего с изменением распределения тепловых потоков по стенкам канала, которое обусловлено изменением трехмерной структуры течения. В случае с 19 реакциями тепловые потоки распределены по-другому, и максимальное локальное значение теплового потока на 70% выше.

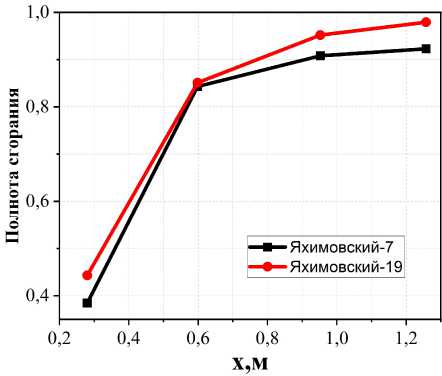
Рис. 6. Продольные распределения тепловой полноты сгорания в канале

4.    Влияние кинетики на результат расчеты дозвукового течения с горением в канале со ступенькой

Теперь рассмотрим влияние модели химической кинетики на моделирование другого эксперимента ONERA, посвященного медленному предварительно перемешанному горению метана со стабилизацией в волне диффузионного пламени. Экспериментальная модель, исследованная Р. Magre и др. [38], представляет собой канал постоянной ширины (0.1 м) с обратным уступом (рис. 7). Вверх по течению от уступа канал имеет длину 1.5 м и высоту 0.065 м, а вниз по течению от ступеньки - длину 1.4 м и высоту 0.1 м. На входе и выходе из канала модели расположены сопла Лаваля со звуковыми сечениями, чтобы лучше контролировать массовый расход и акустику. Уровень турбулентности контролируется хонейкомбом, расположенным в канале вверх по течению. В экспериментах были сделаны шлирен-фотографии течения, измерялось давление на стенке, брались образцы газа для последующей хроматографии с целью получения профилей средних концентраций в области пламени. Также в ходе эксперимента были детально измерены профили скорости и уровень турбулентности с помощью лазерной доплеровой анемометрии (ЛДИС); также с помощью когерентной антистоксовой Рамановской спектроскопии (CARS) измерялись температура и ее пульсации.

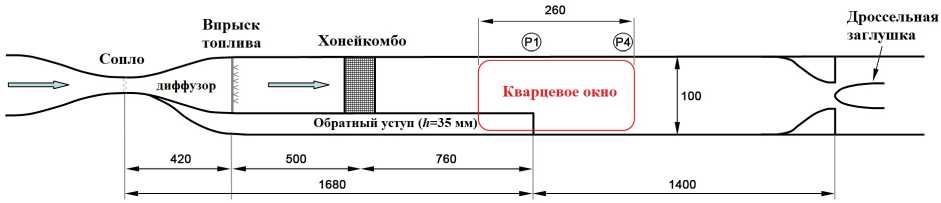
Рис. 7. Схема экспериментальной модели ONERA/LAERTE с уступом

На вход в канал экспериментальной модели поступает предварительно перемешанная смесь метана с воздухом (коэффициент избытка топлива 0.8) с температурой 525 К, скорость газа на входе близка к 50 м/с. Уровень турбулентных пульсаций, измеренный на расстоянии 0.15 м вверх по потоку от уступа, составлял в эксперименте 11 % от средней скорости течения. Были заданы однородный состав газа (Усн4 = 0.0446557, Yq2 = 0.22269, Kn2 = 0.7326543) и постоянная температура Т = 525 К (число Маха потока близко к 0.1). Температура стенок в соответствии с рекомендациями работы [27] была принята равной 800 К. В расчётах в качестве базовой модели химической кинетики применялись редуци- рованная модель [39] с четырьмя реакциями между 7 компонентами (далее - «Фролов4»), Также был рассмотрен скелетный механизм [40] с 25 реакциями между 16 компонентами (далее - «Smooke25»). Расчеты проводились на базе нестационарных уравнений Рейнольдса (URANS) с постоянным шагом по физическому времени, равным 10-5 с. В данной задаче установления стационарной картины течения не происходит, формируется квазипериодиче-ский режим с колебаниями параметров, поэтому результаты расчета дополнительно осред-нялись по времени. (Такой же подход использовался в расчетах ЦАРИ [22, 27].) Детальное описание расчетной области, входных профилей параметров и сетки можно найти в работе автора [41].

В расчетах ЦАРИ [22, 27] использовались кинетика «Фролов4» и модель турбулентности q — ш. В ANSYS Fluent такая модель турбулентности не реализована, поэтому сначала была предпринята попытка вести расчет течения с горением в модели ONERA на базе модели турбулентности SST, как и в разделе 3. Предварительные расчеты проводились без учета TCI - в квазиламинарном приближении (см. (2)). Однако в расчетах на базе SST с кинетикой «Фролов4» угол наклона пламени к направлению потока оказался существенно меньшим, чем в эксперименте (рис. 8а). Поэтому автор рассмотрел другую модель класса к — ш, реализованную в программе FLUENT - BSL к — ш [37], которая отличается от SST тем, что турбулентная вязкость описывается формулой p_t = рк/ш (F ^ = 1) и стқ і = 2.0 (вместо ^ ^,1 = 1.176 в модели SST). Угол наклона пламени в расчёте по модели BSL к — ш стал больше и приблизился к эксперименту - см. рис. 86.

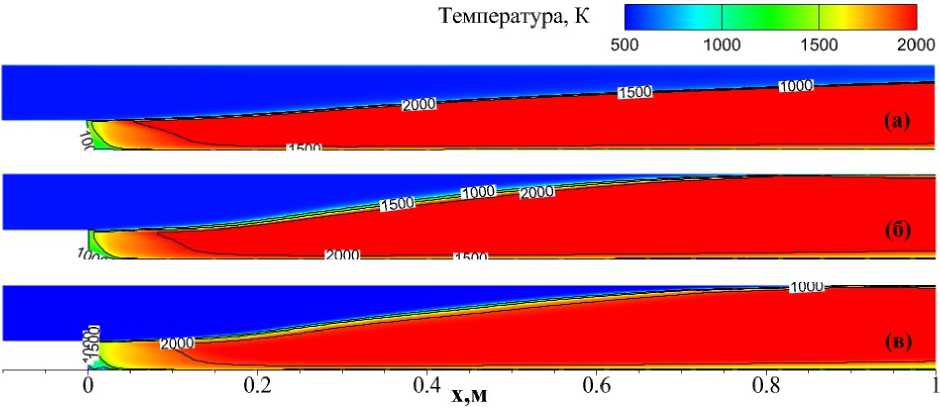
Рис. 8. Поля температуры в расчетах без учета. ТСІ: (а) модель SST, кинетика. «Фролов4»; (б) модель BSL к — ш, кинетика «Фролов4»; (в) модель BSL к — ш, кинетика «Smooke25»

К сожалению, квазиламинарное приближение (рис. 8) приводит к тому, что толщина. фронта, пламени оказывается сильно заниженной. Для получения правильной ширины фронта, пламени необходимо учитывать TCI. Как показано в [25], в данной задаче реализуется режим утолщенного пламени, при котором мелкие турбулентные вихри возмущают внутреннюю структуру пламени. Это оправдывает применимость моделей класса. PaSR в этом течении. В расчетах ЦАГИ [22, 27] использовалась модель EPaSR [26]; поскольку реализовать ее в ANSYS Fluent невозможно, автор принял решение использовать в своих расчетах наиболее близкую простую модель PaSR Хомяка, и Карллсона [24].

В данной задаче при турбулентном горении на. микроскопических масштабах реализуется примерно такой же путь реакции, как и внутри ламинарного пламени. Характерное время химической реакции при прохождении объема, газа, через фронт ламинарного пламени можно оценить по формуле t l = ^ l /Sl , г де 6 l - ширина фронта ламинарного пламени, S l - скорость ламинарного пламени относительно газа. В работе [25] была выполнена оценка величины t l = ^ l /S l при параметрах потока, втекающего в экспериментальную модель

ONERA, и было получено значение 6.09 х 10 ⁴ с. В расчетах ЦАГИ [22, 27] в формуле (7) для повышения устойчивости счета во всем поле течения принималось т_с к = 6.09 х 10^-4 с. Поэтому в предварительных расчетах автора по модели PaSR по кинетике «Фролов4» использовалось это же значение т_с^. Значение коэффициента С_т в оригинальной модели PaSR [24] равно единице. Именно это значение силвно влияет на ширину фронта турбулентного пламени, получаемую в расчетах. В расчетах ЦАГИ [22, 27] с моделвю турбулентности q — ш использовалось значение С_т = 0.2. В расчетах автора с другой моделвю турбулентности (BSL к — ш) для получения правильной ширины фронта турбулентного пламени было подобрано значение С_т = 0.11. Результаты этого расчета представлены на рис. 9 (черная сплошная линия) и на рис. 10а. На рис. 9 показаны осредненные по времени профили температуры в ряде поперечных сечений канала и их сравнение с экспериментом, а на рис. 10 - осредненнвіе по времени поля температуры.

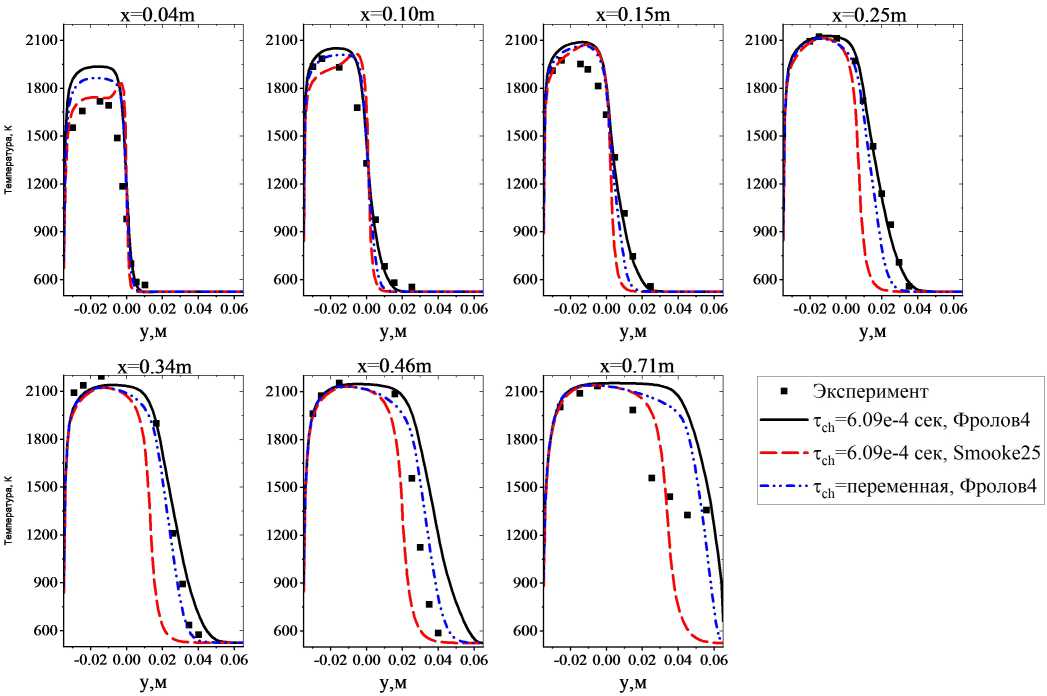
Рис. 9. Сравнение профилей температуры в ряде поперечных сечений канала, полученных в рас четах с использованием модели PaSR

После этого была предпринята попытка моделирования данного течения с использованием модели PaSR ( т_с ^ = 6.09 х 10^-4 с, С_т = 0.11) на основе скелетного механизма «Smooke25». Результаты расчета представлены на рис. 9 (красная пунктирная линия) и на рис. 10в. Очевидно, что при использовании намного более точной, многостадийной кинетики «Smooke25» угол наклона пламени стал намного меньшим, чем в других расчетах, и фронт пламени стал более узким, чем в эксперименте. Попытка улучшить результат за счет дробления сетки в 100 раз не увенчалась успехом.

Тогда было сделано предположение, что для скелетного механизма «Smooke25», который способен корректно описывать промежуточные этапы развития реакции, приближение тси = const является слишком грубым. Чтобы оценить возможный эффект от перехода к переменным значениям тс^, зависящим от локальных условий течения, была реализована простая модель, в которой характерное время химических процессов оценивается по формуле

T ch =

Y H 2 O

^S H 2 O /P

(И)

где Sh₂o - локальное значение химического источникового члена в уравнении для массовой доли паров воды. Модель (11) используется во многих работах - см., например, [42]. Чтобы убедиться в адекватности работы этой модели, сначала был выполнен расчет по кинетике «Фролов4» с переменным значением т_сһ, рассчитанным по формуле (11). Результаты показаны на рис. 9 (синяя пунктирная кривая) и на рис. 106. Существенного изменения решения не произошло. Следовательно, формула (11) предсказывает разумные значения т_сһ-

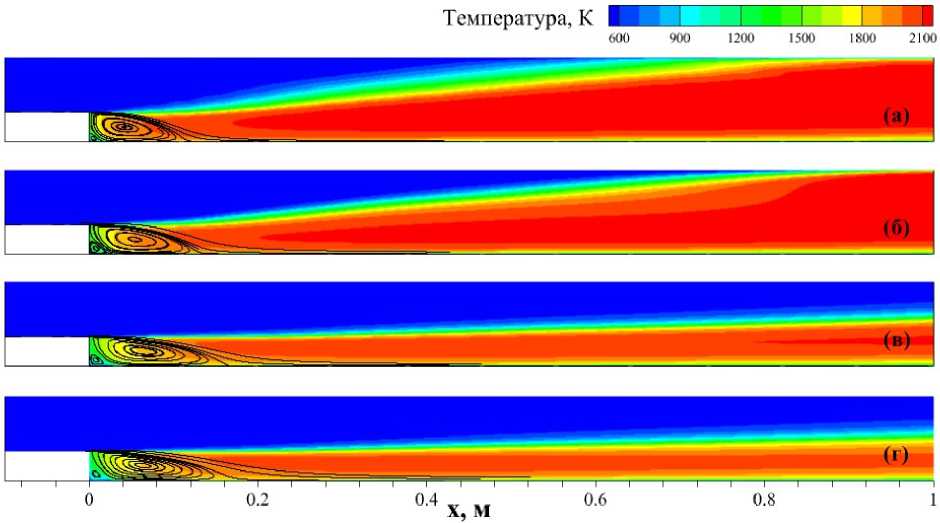
Рис. 10. Поля температуры, полученные в расчетах па. базе модели PaSR с использованием различных кинетических схем: (а) «Фролов4», т _с һ = 6.09 х 10^-4 с, (б) «Фролов4» с переменном значением T _ch- (в) «Smookc25». т _с һ = 6.09 х 10^-4 с. (г) «Smookc25» с переменном значением т _с ^- Показаны зоны рециркуляции

После этого был выполнен расчет по кинетике «Smooke25» с использованием формулы (11). Получилось поле температуры, показанное на рис. Юг. Как и в случае кинетики «Фролов4», переход на. формулу (11) не привел к существенному изменению результатов. Таким образом, гипотеза, о необходимости уточнения при работе со скелетным механизмом не подтвердилась. Однако попытка, провести расчет по кинетике «Smooke25» без учета. TCI (в квазиламинарном приближении) дала, нормальный угол наклона, фронта, пламени - см. рис. 8в. Следовательно, проблема заключается не в самом кинетическом механизме «Smooke25», а. в его взаимодействии с моделью турбулентного горения PaSR.

В данной задаче реализуется волна, горения, распространяющаяся по газу за. счет диффузионных потоков тепла, и массы от продуктов сгорания к холодной смеси. Эти потоки существенно ускоряют протекание реакций и меняют путь химической реакции, добавляя вещества, которых нет в исходной смеси (в том числе - радикалы). Этому пути реакции т,..-,"

соответствует повышенное значение интеграла тепловыделения Iheat = J w(T)q(T)dT, т где ш(Т) - 'зависимость скорости суммарного процесса СИд + 2С)2 ^ С'02 + 2Н2О от температуры, соответствующая данному пути реакции, Тнач - температура перед фронтом пламени, Ткон - температура за фронтом пламени, q(T) - тепловой эффект суммарного процесса, при заданной температуре. Именно этот интеграл определяет локальную скорость волны горения относительно исходной смеси, которая согласно теории Зельдовича, и

Франк-Каменецкого [43] приближенно выражается формулой

S

2Ш^

^нач С р ( Ткон - т_пач

где А = цс_р/ Pr - коэффициент теплопроводности.

Редуцированный механизм «Фролов4» не воспроизводит путв реакции, но обеспечивает правильное значение интеграла тепловыделения. Поэтому и в квазиламинарном расчете, и в сочетании с моделью PaSR кинетический механизм «Фролов4» позволяет получить правильный угол наклона фронта пламени (этот угол определяется скоростью волны горения относительно исходной смеси).

Скелетный же механизм «Smooke25» позволяет получить разные пути реакции. Если этот механизм используется в квазиламинарном расчете (без модели PaSR), то в этом расчете непосредственно воспроизводятся турбулентные диффузионные потоки тепла и массы из зоны горения вверх по потоку, и механизм «Smooke25» выходит на правильный путь реакции, дает правильное значение интеграла тепловыделения и правильный угол наклона волны горения. Если же механизм «Smooke25» используется в сочетании с моделью EDC [23] или PaSR [24], то химический шаг алгоритма описывается уравнениями (3), которые являются локальными и не содержат диффузионных потоков. При этом уравнения (3) соответствуют процессу с характерным временем т *, которое гораздо больше времени пребывания объемов газа внутри фронта турбулентного пламени. Поэтому этот химический процесс, не учитывающий диффузию, развивается по другому пути, который отличается от реального и дает гораздо меньшее значение интеграла тепловыделения, а значит, и гораздо более пологий наклон фронта пламени.

Таким образом, при использовании многостадийных кинетических механизмов в сочетании с моделями TCI необходимо следить за тем, что химическая реакция будет развиваться по правильному пути. В случае квазистационарных моделей EDC и PaSR, описываемых локальными уравнениями (3), обеспечить правильный путь реакции невозможно, поэтому лучше использовать эти модели TCI в сочетании с упрощенными кинетическими схемами, обеспечивающими верное значение интеграла тепловыделения. Если же модель TCI позволяет учесть пространственные процессы (как, например, модель EPaSR [26]), то многостадийные кинетические механизмы должны работать нормально.

5.    Заключение

В статье на основе воспроизведенных в расчете двух классических экспериментов проанализировано влияние кинетических механизмов на результаты моделирования турбулентных течений с горением в каналах.

Решена задача о высокоскоростном неперемешанном турбулентном горении водорода в экспериментальной модели ONERA LAPCAT II. Установлено, что при моделировании высокоскоростного горения в канале с преимущественной ролью самовоспламенения модель химической кинетики мало влияет на распределение давления по стенкам канала, но оказывает значительное влияние на трехмерную структуру течения. Это приводит к различиям в предсказании распределения и величины тепловых потоков, а также полноты сгорания топлива. Тепловые потоки могут отличаться на 70%, полнота сгорания - на 5%.

Также решена задача о дозвуковом предварительно перемешанном турбулентном горении в экспериментальной модели ONERA с обратным уступом. Показано, что при переходе к другой модели турбулентности необходима настройка коэффициентов модели турбулентного горения PaSR. Выполнена настройка PaSR для работы с моделью BSL к- ш. Достигнуто качество моделирования турбулентного диффузионного пламени в канале, не уступающее качеству, полученному в лучших расчетах ЦАРИ с использованием модели EPaSR.

Установлено, что модель PaSR более точно описывает турбулентное диффузионное предварительно перемешанное пламя при использовании глобальных, а не многостадийных кинетических механизмов. Модель PaSR, в уравнениях которой нет молекулярной диффузии и других пространственных процессов, при использовании детального кинетического механизма дает неверный путь реакции (с другим интегралом тепловыделения). Рекомендуется при описании данного течения использовать модель PaSR с кинетическими механизмами, которые обеспечивают правильную величину интеграла тепловыделения.

Работа выполнена при финансовой поддержке Китайского Стипендиального Совета (договор № 201606120286)