Влияние нелинейных элементов с гистерезисом на устойчивость замкнутых систем

Среди методов анализа устойчивости замкнутых нелинейных систем (ЗНС) особое место занимает метод гармонической линеаризации (МГЛ). Этот метод в сочетании с критерием устойчивости Найквиста позволяет проанализировать устойчивость ЗНС и даже определить амплитуду и частоту автоколебаний [1; 2]. На рис. 1 приведена структурная схема ЗНС, для анализа устойчивости которой можно применить МГЛ в сочетании с критерием устойчивости Найквиста.

Условием применения МГЛ для анализа ЗНС является наличие в схеме фильтра нижних частот (ФНЧ), который включен после нелинейного элемента (НЭ). Заштрихованный сектор в сумматоре на рис. 1 соответствует умножению сигнала обратной связи на -1. Наличие в схеме ЗНС фильтра нижних частот предполагает, что он без ослабления пропускает первую гармонику и не пропускает на выход высшие гармоники сигнала с выхода НЭ. В этом случае на выходе ФНЧ будут присутствовать только первые гармоники синуса и косинуса сигнала с выхода НЭ [1; 2]:

yвых = q(A)Asinϕ + q1(A)A cos ϕ, (1) где А, ϕ = ωt – амплитуда и текущая фаза гармонического сигнала на входе НЭ; q(A), q1(A) – коэффициенты ряда Фурье для первой гармони- ки синуса и косинуса соответственно, которые определяются по формулам [1; 2]:

π

q ( A ) =       y sinϕ d ϕ,

π A

-π

π q1(A) =       ycosϕdϕ,

π A -π

где y – сигнал на выходе НЭ при входном воздействии x = A sin ϕ при изменении фазы ϕ от

-π до π.

Перейдем от гармонического сигнала на выходе ФНЧ к комплексному сигналу с учетом указанных выше свойств ФНЧ:

Y вых ( j ϕ) = X ( j ϕ) W н ( jA ),                        (4)

где W _н( jA ) – комплексный коэффициент передачи НЭ, определяемый по формуле

W н ( jA ) = q ( A ) + jq 1 ( A ).                           (5)

Множитель на мнимую единицу j в формуле (5) отражает сдвиг фазы косинуса относительно синуса. Использование в формулах (1)–(4) текущей фазы ϕ = ω t означает, что НЭ не обладает инерционностью. Если это условие не выполняется, то инерционные характеристики НЭ переносят в ФНЧ.

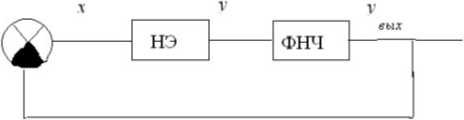
Рис. 1. Структурная схема замкнутой нелинейной системы

1. Разновидности характеристик нелинейных элементов с гистерезисом

На рис. 2 приведены характеристики НЭ с гистерезисом трех видов: релейного ( а ), гладкого ( б ) и кусочно-линейного ( в ). Характеристика

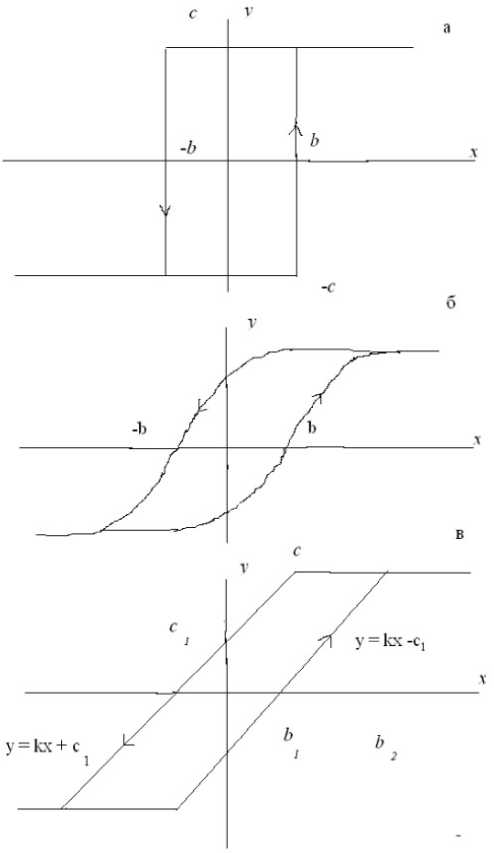
Рис. 2. Характеристики нелинейных элементов с гистерезисом релейного ( а ), гладкого ( б ) и кусочно-линейного вида ( в )

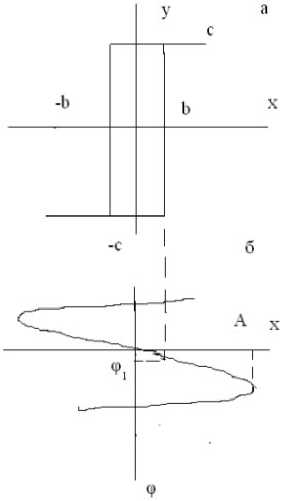
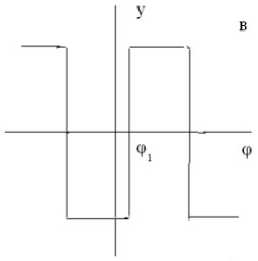
Рис. 3. Характеристика НЭ релейного вида ( а ), сигналы на входе НЭ ( б ) и на выходе НЭ ( в )

на величину Q i . Величина Q i определяется из равенства, следующего из рис. 3, б :

на рис. 2, в является кусочно-линейной аппроксимацией характеристики на рис. 2, б .

Особенностью характеристик НЭ с гистерезисом является то, что выходной сигнал в них изменяется в зависимости от того, в какую сторону изменяется сигнал на входе НЭ.

2. Определение коэффициентов ряда Фурье для НЭ с гистерезисом

В соответствии с формулами (2) и (3) вначале получим выражения для коэффициентов q ( A ), q ₁( A ) для НЭ с гистерезисом релейного вида рис. 2, а . На рис. 3 приведены характеристика НЭ релейного вида ( а ), сигналы на входе НЭ ( б ) и на выходе НЭ ( в ).

Из сопоставления рис. 3, б и в видно, что сигнал на выходе НЭ искажается по форме и запаздывает по фазе относительно входного сигнала

A sin Q i = b ,

откуда

b

Q i = arcsin —.

В интервале изменения фазы Q от -п до п сигнал на выходе НЭ изменяется от - C до С трижды:

на участке от -п до -п + Q i сигнал y = C ;

на участке от -п + Q i до Q i сигнал y = - C ;

на участке от Q i до п сигнал y = C .

Используя формулу (2) и значения сигнала y на трех участках изменения текущей фазы Q от

-п до п, получим:

q ( A )

п A

f -^+Qi

I

V ^-п

C sin q d q -

-

I

C sin q d q + | C sin q d q =

4 C       4 C

=---cos m i =      1

п A      п A

—

b ²

A 2 .

Используя формулу (3) и значения сигнала у на трех участках изменения текущей фазы ф от —п до п, получим:

q 1 ( A )

п A

Г ^—п+Ф1

I

C cos ф d ф —

—

f

—п+ф ₁

V —п

C cos ф d ф + f C cos ф d ф =

ф1

4C sin ф1

—4 bC

"A²^ ^.

Отметим, что полученные для коэффициентов q ( A ), q 1 ( A ) выражения (7) и (8) при b — 0, что означает отсутствие гистерезиса, превращаются в известные формулы для коэффициентов q ( A ), q ₁( A ), полученные для идеального ограничителя [2]:

q ( A ) = —, q 1 ( A ) = 0. п A

Теперь получим выражения для коэффициентов q ( A ), q ₁( A ) для НЭ с гистерезисом кусочнолинейного вида рис. 2, в . На рис. 4 приведены характеристика НЭ кусочно-линейного вида ( а ), сигналы на входе НЭ ( б ) и на выходе НЭ ( в ).

Из рис. 4, а , б следуют соотношения:

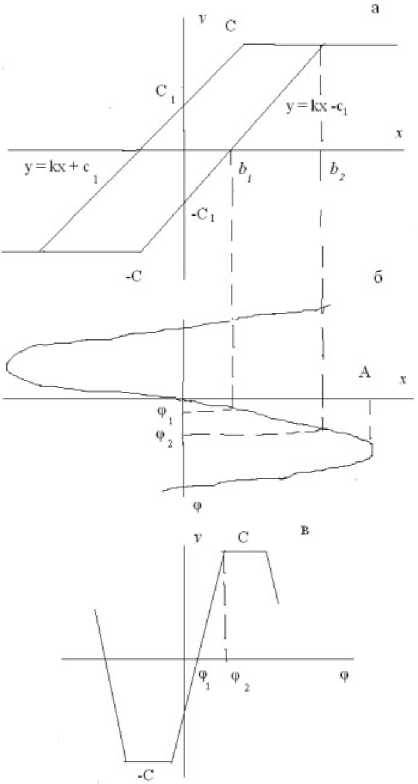
Рис. 4. Характеристика НЭ кусочно-лнейного вида ( а ), сигналы на входе НЭ ( б ) и на выходе НЭ ( в )

A sin ф₁ = b ₁,   A sin ф₂ = b ₂ ,

k — C ₁/ b ₁, C ₁ = C /2.

Из построений на рис. 4 видно, что сигнал на выходе НЭ запаздывает относительно входного гармонического сигнала на величину ф 1 . В интервале изменения фазы ф от —п до п сигнал у изменяется таким образом:

на участке от —п до —п + ф 2 сигнал у убывает от C 1 до — C ;

на участке от —п + ф 2 до —ф 1 сигнал у — — C ;

на участке от —ф 1 до ф 2 сигнал у возрастает от

— C до С ;

на участке от ф 2 до п — ф 1 сигнал у — C ;

на участке от п — ф₁ до п сигнал у убывает от C до C ₁.

Используя формулу (2) и значения сигнала y на пяти участках изменения текущей фазы ф от

п—ф1

+ f

ф2

—п до п, запишем:

q ( ^A )=4 п A

( ^—п + ф 2

I

V —п

( kA sin ф + C 1 ) sin ф d ф —

C sin ф d ф +

п

f

п—ф ₁

)

( kA sin ф + C 1 ) sin ф d ф

J

После вычисления интегралов получим:

k (              1 . „       1 . „ )

q ( A ) —   ф^ + ф₂ sin 2ф^--sin 2ф +

п(          2          2       ;

2 C               C

+--(cos ф} + cos ф2) +--(cos ф2 — cos ф}).

п A             п A

Используя формулу (3) и значения сигнала у на пяти участках изменения текущей фазы ф от

—п до п, запишем:

q 1^{( A} )=Л" п A

Г ^—п + ф 2

f

V —п

( kA sin ф + C 1 ) cos ф d ф —

—ф ₁

f

ф2

C cos ф d ф + f ( kA sin ф — C 1 ) cos ф d ф +

—п + ф2

—ф1

—ф1

f

ф2

C sin ф d ф + f ( kA sin ф — C 1 ) sin ф d ф +

п—ф ₁

+ f

C cos ф d ф +

—п+ф2

ф2

f ( kA sin ф + C 1 ) cos ф d ф

J

п—ф ₁

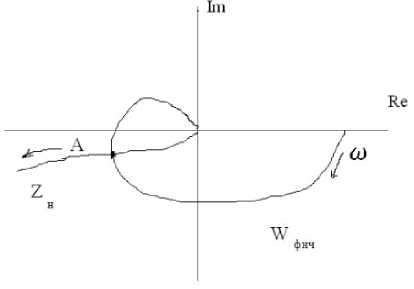
Рис. 5. Годограф ФНЧ W ф _нч ( j ш ) и годограф Z _н ( jA ) = - 1 / /( W н ( jA ))

После вычисления интегралов получим: k q1 (A) =    (cos 2ф1 - cos 2ф2) +

2п

2 C                2 C

+--(sin ф! - sin ф2 ) +--(sin ф! - sin ф2 ).

п A             п A

Если в НЭ на рис. 2, в наклонные прямые сливаются в одну прямую, т. е. гистерезис исчезает, тогда получим формулы для расчета коэффициентов q ( A ), q ₁( A ) для усилителя-ограничителя:

C             4 C

q ( A ) = — (2ф 1 - sin 2ф 1 ) + — cos ф 1 ,

• п b              п A

• 3. Определение амплитуды и частоты автоколебаний в замкнутых нелинейных системах с гистерезисом

qi( A) = 0, где ф1 определяется по (6).

В соответствии с МГЛ и критерием устойчивости Найквиста автоколебания в ЗНС возникнут при выполнении условия:

W фнч ( j ш) W h ( jA ) = -1.

Это условие можно переписать в виде

W фнч ( j ш) =

-1

. W н ( jA )

Используя полученные в статье выражения для коэффициентов q ( A ), q ₁( A ), можно определить амплитуду и частоту автоколебаний в ЗНС с характеристиками НЭ вида рис. 2, а , в . Для этого на комплексной плоскости надо построить два годографа (рис. 5): годограф ко мп лексного коэффициента передачи ФНЧ W ф _нч( j ш) в зависимости от частоты ш и годограф звена, комплексный коэффициент передачи которого в зависимости от амплитуды А определяется по формуле [1; 2]

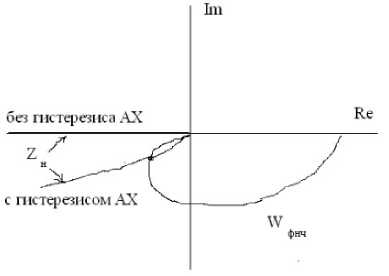
Рис. 6. Годограф ФНЧ из двух RC-цепочек W фнч ( j ш ) и годографы Z н ( jA ) = - 1 / ( W _h( jA )) для компаратора без гистерезиса и с гистерезисом амплитудной характеристики

Z н ( jA ) =

-1

W н ( jA )

-1

.

q ( A ) + jq ₁( A )

Точка пересечения этих двух годографов определяет амплитуду A _к и частоту автоколебаний ш_к, которые можно рассчитать как аналитическими, так и численными методами. Если указанные годографы не пересекаются, то ЗНС будет устойчивой.

Заключение

Нелинейные элементы с гистерезисом, кроме искажений формы сигнала, создают его запаздывание по фазе на величину ф 1 . Это обстоятельство может привести к самовозбуждению в замкнутых системах, в которых с позиций линейной модели по критерию Найквиста самовозбуждения возникать не должно. Эксперимент подтверждает, что охваченный цепью обратной связи (ОС) компаратор, в цепи ОС которого включены две RC-цепочки (они выполняют роль ФНЧ), генерирует автоколебания из-за наличия в его амплитудной характеристике (АХ) гистерезиса (рис. 2, а ). Компаратор без гистерезиса АХ с такой схемой ОС не будет генерировать автоколебания, так как годографы

1                -кА

Wфнч (jш) =----- и Zн (jA) = —- ф        (1 + j ш RC )2             4 C в этом случае не пересекаются (см. рис. 6).