Влияние нестационарных возмущений на отделение тонкого тела

• 1.    Постановка задачи

• 2.    Метод решения, вычисление силы и момента

  

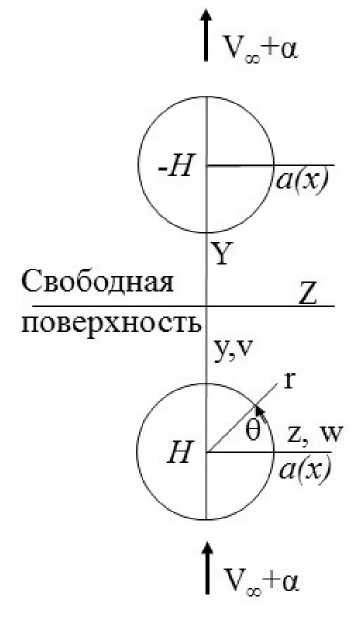
  Рис. 2. Задача, со свободной поверхностью в фазе 3

  
  

Нестационарное взаимодействие тел является весьма, актуальной задачей аэромеханики, имеющей многочисленные практические приложения, такие, как отделение груза, из каверны или с внешней подвески носителя, аэродинамическое взаимодействие многих тел [И- В последнее время нестационарность нагрузок, обусловленная нелинейным возбуждением акустических волн Росситера. [5] в каверне при транс- или сверхзвуковом полете, приобрела, значительный интерес, на. что указывает появление новых экспериментальных исследований. Расчетные исследования базируются на. эмпирических данных по измерениям стационарных нагрузок [2], аналитическом подходе [1-4, 10], а. также численных методах к решению аэродинамической задачи. Использование полуэмпирических методов приводит к ошибкам, которые не позволяют проанализировать возможные явления, например, бифуркации траектории [2]. Трудности численного моделирования обусловлены сложностью

аэродинамической задачи и временными затратами, что препятствует его использованию в прикладных расчетах. Аналитический подход [1-4] требует минимальных временных затрат и достаточно хорошо согласуется с экспериментальными данными при дозвуковых скоростях. В настоящей работе предложено его расширение на случай наличия нестационарных возмущений вертикальной скорости набегающего потока. Представлена формулировка задачи определения подъемной силы и вращающего момента, метод решения и его верификация на основе сравнения результатов расчетов с экспериментальными данными для отделения тонкого тела вращения из каверны в сверхзвуковой поток.

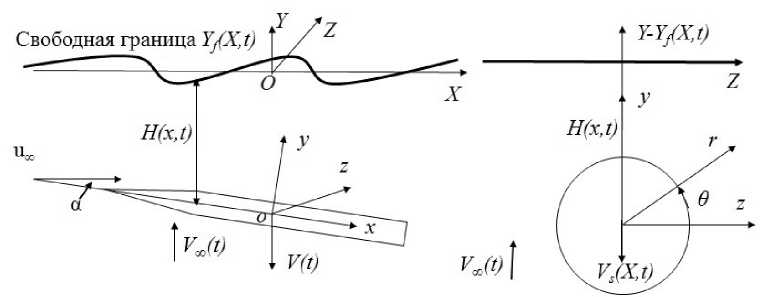
Рис. 1. Общая схема, задачи движения тела, в фазе 3

Так что влиянием вязкости на. эти параметры движения можно пренебречь, а. слой смешения между каверной и потоком считать поверхностью разрыва продольной скорости. Предполагается, что влияние боковых стенок каверны невелико и они не рассматриваются. При отделении из каверны движение тела, подразделяется на. три фазы: фаза. 1 - движение внутри каверны, фаза. 2 - пересечение телом слоя смешения и фаза. 3 - движение в потоке. При внешнем отделении от твердой поверхности остается только фаза. 3.

Общая схема, задачи для фазы 3 отделения из каверны представлена, на. рис. 1. Продольные координаты X (начало на передней стенке каверны) и ж (начало в центре массы тела) отнесены к длине тела 1, поперечные, У и Z (связанные с каверной), а также у II z (связанные с осью тела.) - к характерной толщине тела. 51; время t отнесено к l/u^. u^ - скорость набегающего потока. Центр массы тела о движется с вертикальной скоростью 5u^V (t), скорость движения каждой поперечной плоскости 5u^V_s(t), зависит также от скорости вращения тела lш(t)/(5u_ro) : V_s(X,t) = V(t)- жш(Х, t); ш = da/dt, 5a - угол атаки. На тело натекает однородный нестационарный вертикальный поток 5u^V^ (t), а разделительная поверхность на границе каверны определяется функцией 51Уу (X, t). В плоскости поперечного сечения рассматриваются также цилиндрические координаты г и Ө. В рамках теории тонкого тела, задача, обтекания формулируется для потенциала, течения:

Ф* = lu^, {ж + 5² [A_O(X, t) + Ф(ж, у, z, t)] }.

Потенциал возмущений Ф(ж, у, z, t) удовлетворяет уравнению Лапласа в каждой плоскости поперечного сечения ж = const и краевым условиям:

XX ⁺ XX = 0, ^у = Уу ^(ж,^t) : р⁺ = р^-, dz²   ду²

д2Ф г = ° : ,. = °^; у ^ дг2

-

то :    ^ У(ж,Ц = V^(t) + a(t) + ш(t)ж - V(t).

ду

р . и р- - давление в каверне и в потоке на свободной поверхности. Давление связано с потенциалом соотношением

_ Р* - Р^

Р  52 Р^о

Г дА о дА о д Ф д Ф

[   + ах + а? + дХ +

1 /2

2 Р

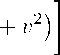
Здесь Ао(х,У) - известная функция, для фазы 1 А о (х,? _ 0.

Для решения задачи обтекания в плоскости поперечного сечения для фаз 1 и 3 используется аналитическое продолжение нижней (фаза. 3) или верхней (фаза. 1) полуплоскости и метод мультипольного разложения, предложенный Н.Е. Кочиным для решетки профилей [14]. Задача, сводится к конфигурации, представленной на. рис. 2. Решение для комплексно-сопряженной скорости W (Х, А,?) представляется суммой двух интегралов Коши по контурам основного и отраженного тел:

W (Х)_^ / 2гтг у

Н=1

WHr+JsK    1 Г W(гт + £ X . _ Z + гҮ

Н (Х,? а(х)

А + гт — £      2гг ] А — гт — I ¹      а(х)

| t | =i

Переходя в систему координат, связанную с центром поперечного сечения тела, с помощью преобразования s _ А + гт, и разлагая ядра интегралов в ряды по s, получим представление решение в виде сингулярных рядов Лорана по А + гт и А — гт. Коэффициенты этих рядов С_—п—1 _ А_—п—1 + гВ_—п— 1 и С_—п— 1 _ А_—п—1 — гВ_—п— 1 определяются условиями аналитического продолжения и краевыми условиями (1):

^А - 2п - 1

(— i)2£²2 \^ ^{(2т + 2}^ —^1)! _{т 2т} ±(2п — 1)!            2rn!      ⁽   ) ^q

2т + 2п

^А- 2 т- 1 ⁺ "Д--- Г^В<1В — 2 т— 2   ,

2т + 1

т=0

В- 2п - 2

(—1)ng2n+1 ү^ (2т+_2п)!

(2п)!              2т!    ()

'' т=0

^А- 2т - 1 +

2т + 2п + 1

2т + 1

qB- 2m -2^ ,

^А- 2п ^— 0,   ^В- 2н - 1 ^— О,

В — В- 2 — V , ± 7 £ (—1)^тд^2т (А- 2 т- 1 + дВ- 2 т- 2 ), д(Х, t) — ₂ ДД) 6 2.   (3)

С точностью O(q 9 ) решения этих уравнений получены в явном виде [2]. Аналогичные результаты получены для фазы 1.

Схема движения тела при пересечении свободной поверхности показана на рис. 3. Можно выделить три характерных области тела (рис. За): область 21 движется в фазе 1 внутри каверны, область 22 частично находится в каверне и частично в потоке, а область 23 расположена полностью в потоке. Область 21 соответствует движению в фазе 1, область 23 - в фазе 3, и описываются представленными выше соотношениями.

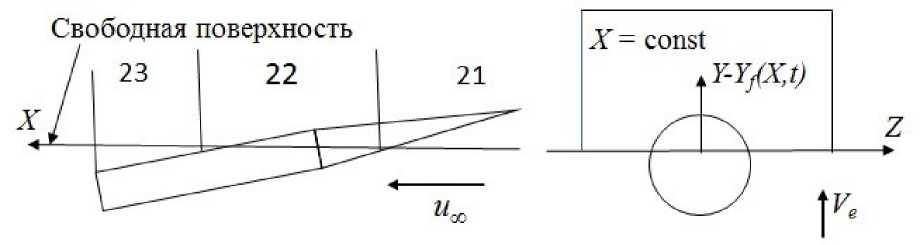
а) вид сбоку;

б) вид спереди;

Рис. 3. Схема, движения тела, в фазе 2

Плоскость поперечного сечения в области 22 представлена, на. рис. 36. Здесь верхняя часть круга, находится в каверне, а. нижняя - в потоке. Решение задачи (1) находится раздельно для каждой из частей круга, с использованием аналитического продолжения и отображения получившейся фигуры из двух симметричных частей круга, на. плоскость. Решение подобно полученному ранее при отсутствии нестационарных возмущений поверхности [2].

Подъемная сила L(t) и момент вращения М (t) определяются в следующей форме:

L_x(x,t) — —а (х) j р sin ӨdӨ, L(t) — ^ L_x(x,t)dx, М (t) — j L_x(x,t)xdx.

0                           хо                             хо

Для фазы 2 получены достаточно сложные соотношения, включающие специальные функции [2]. Для фазы 3 локальная подъемная сила Lx(t) определяется соотношением

Lx

—7Г

f д [(2В — V,) а²] дх

+ а^{2 д (2В  V , )} — 2 (в — р_е) аа х + 2В А_-3а—

∞

—2а £ (А- 2 „- 1

П =1

—

^А- 2 п- з ) ^В- 2п - 2

I

Подъемная сила, и момент находятся из соотношений

L(t) —

+2г 7 [ хо 1_

— Щд^ + L i (t),   L i (t) — —га² (х,) [2В (х, ,t) — V , (х , , t)] +

∞

^{(В — V} e ^{) а} х ^{— ВА}- 3 ⁺ ^ ^{( А} - 2п - 1 п=1

—

^А - 2п - 3

) В- 2 _П- 2^ а(x)dx,

^М ^ = - """^ ⁺ ^^ ^M 1 (t = Va — ^a 2 (x e )x e [2 В(xe, t) - V e (x e ,t)] +

+2л

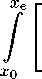
^{(В —} V , ) a_x

∞

^{— ВА}- з ⁺ ^^ ⁽Х- 2 „- 1

П =1

-

^А- 2п - 3

.в 1

) ^В- 2п - 2

a(x)xdx,

V_a(t) = л J [2B(x,t) — V_e(x,t)] a²(x)dx, w_a(t)=^ j [2B(x,t) — V_e(x, t)] a²(x)xdx. Ж0                                                       X 0

Подстановка в соотношения (5) приближенных значений коэффициентов Лорана ти-

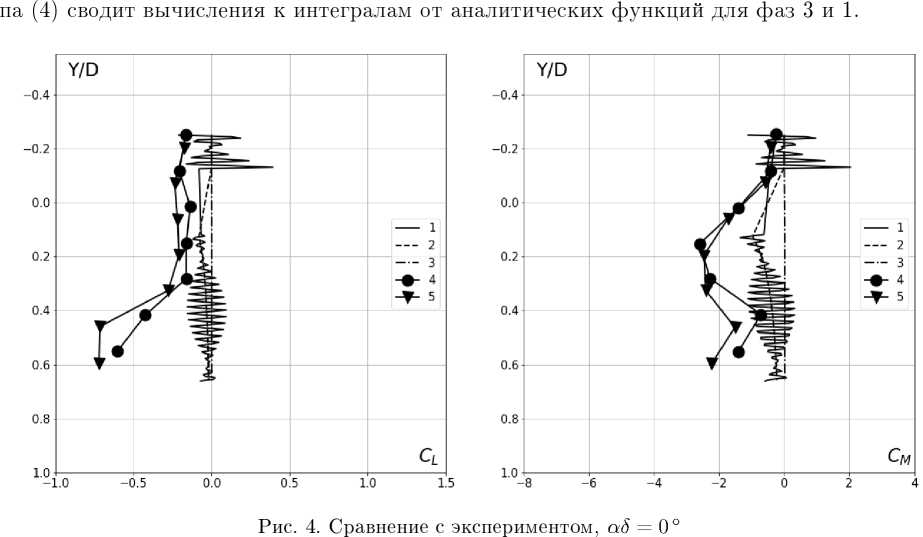
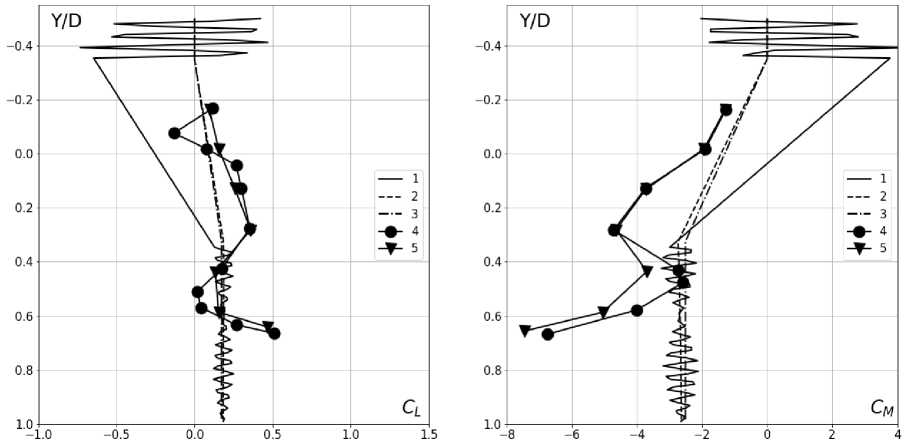
Рис. 5. Сравнение с экспериментом, а5 = —5°

Для фазы 2 подъемная сила и момент описываются достаточно сложными выражениями, включающими интегралы от специальных функций [2]. Учет возмущений свободной поверхности приводит к дополнительным слагаемым в выражениях для давления, силы и момента. Однако, как показал анализ, их влияние на параметры движения тела несущественно [10]. Поэтому в настоящей работе для верификации метода использовались расчеты только для фаз 1 и 3, а фаза 2 не рассматривалась.

Рассматривалось простейшее представление акустических возмущений в каверне и около нее (моды Росситера) в виде фундаментального решения линейного гиперболического уравнения. Здесь изменениями волн в направлениях X и Ү пренебрегается, так как их масштабы много больше поперечного размера тела; П - безразмерная частота моды Росситера, А - ее безразмерная амплитуда. Последние параметры находились из экспериментальных данных [7]. На рис. 4 и 5 представлено сравнение расчетов с измерениями [7] коэффициентов подъемной силы C l и вращающего момента См-

C_L = ²⁶ L (—V_e), См = ¹ М (—V_e) 7Г                             7Г

Эксперименты включают измерения силы и момента для углов атаки аб = 0° и -5° для постоянных скоростей перемещения тела V = 0.349377 м/с (кривые 4) и V = 0.0349377 м/с (кривые 5) от положения в каверне Ү/D = —0,25 до положения в потоке Ү/D = 0,6. Расчеты выполнены при V = 0.349377 м/с для случаев отсутствия возмущений в безграничном потоке (кривые 3), с учетом влияния свободной границы с возмущениями (кривые 1) и без них (кривые 2). Анализ экспериментальных данных показал, что амплитуда возмущений в каверне и потоке отличается заметно, ее отношение к 6ui_nj_ty в каверне А = 7.95, а в потоке 1.76. Следует обратить внимание на достаточно большой разброс экспериментальных данных, что, по-видимому, обусловлено именно влиянием нестационарных вертикальных возмущений. Представленные на рис. 4 и 5 результаты показывают достаточно удовлетворительное согласие расчетных и экспериментальных данных, несмотря простоту используемой модели.