Влияние околососудистой среды на механические свойства артериальной стенки

В настоящее время существует множество моделей механических свойств стенок артериальных сосудов (как в рамках линейной изотропной, так и нелинейной анизотропной теории упругости [1]), достоверно приближающих свойства реальных объектов [2-6]. Достаточно полные обзоры таких моделей приведены в работах [7] и [8]. Но еще не получила широкой известности ни одна модель, в которой бы учитывалось воздействие околососудистой среды на напряженно-деформированное состояние стенки сосуда.

Целью данного исследования является построение теории напряженно-деформированного состояния стенки артериального сосуда с учетом воздействия околососудистой среды на основе наиболее полной и достоверной на данный момент модели механического поведения артериальной стенки, предложенной в [8].

Артерия представляется как двухслойная толстостенная трубка, состоящая из двух слоев: media (средний слой артерии) и adventitia (наружный слой). Это - главные механически важные компоненты здоровой артерии. Третий слой (intima) не рассматривается.

Каждый слой образован неколлагеновой матрицей, которая рассматривается как изотропный материал, и двумя семействами коллагеновых волокон, спиралевидно закрученных вдоль артериальной оси и расположенных симметрично относительно нее

(но с разной ориентацией в двух слоях). Эти волокна порождают анизотропию в механическом смысле.

Так как артериальные ткани не изменяют свой объем в пределах физиологического диапазона деформаций, с точки зрения механики они могут рассматриваться как несжимаемые материалы.

Модель и методы

Артерия представляется как двухслойный нелинейно-упругий полый цилиндр с винтовой анизотропией, содержащий дисклинацию (рис.1). Рыхлая волокнистая соединительная и мышечная ткани, окружающие сосуд, моделируются упругой средой, обладающей свойствами винклеровского основания [5, 6]. Цилиндр подвержен деформации растяжения, раздувания и кручения. Рассматривается случай, когда внешняя среда сопротивляется только радиальным перемещениям стенки сосуда.

Деформация цилиндра задается соотношениями:

R = R(r),

< Ф = Кф + ф Z,

Z = к z.

г0 < г < г2, 0 < ф < 200°.

Здесь г, ф, z - цилиндрические координаты отсчетной конфигурации, R, Ф, Z - цилиндрические координаты текущей конфигурации.

Соответственно, тензор градиента деформации представляется в виде [1]:

C = R'e_re_R + —к е_фе_ф+^ф е₂е_ф+Хе₂е₂.                 (2)

Г

Здесь q^s - материальные криволинейные координаты; Q^M - пространственные криволинейные координаты; г⁵ - векторы взаимного материального базиса в

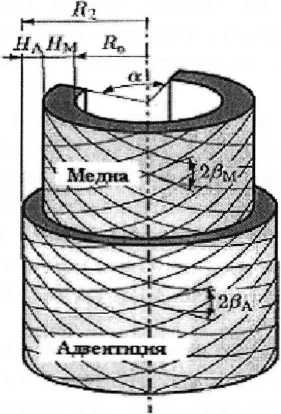
Рис. 1. Представление артерии как двухслойного цилиндра

отсчетной конфигурации; R_M - векторы материального базиса в текущей конфигурации; е_г, е_ф, e_z - орты, касательные к координатным линиям цилиндрических координат г, ф, _z; e_R, е_ф, e_z - орты, касательные к координатным линиям цилиндрических координат.

Кроме того, имеют место следующие соотношения:

e_R = е_г со8(Ф-ф) + е_ф зт(Ф-ф), е_ф = -е_г зт(Ф-ф) + е_ф соз(Ф-ф), ez=e_z-

Мера деформации Коши имеет вид:

Компоненты тензора градиента деформации в смешанном базисе и компоненты меры деформации Коши в базисе отсчетной конфигурации цилиндрической системы координат являются функциями только радиальной координаты г.

Материал цилиндра считается анизотропным и несжимаемым. Функция удельной потенциальной энергии деформации представляется выражением [8]:

где Z4y =AlyoG, Z6y=A2yoG, Z^trG, А1у=а1уа1у, А2у=а2уа2уи

О

aU =

COS р у ^ПУ

а2у -

COSpy

,"™1У

где у = А,М (адвентиция и медиа, соответственно). Углы ру в (4) характеризуют наклон коллагеновых волокон (см. рис. 1).

Таблица 1

Материальные и геометрические данные для сонной артерии кролика [8]

	Материал	Геометрия
Медиа	См = 3 кПа кхм = 2,3632 кПа к2М =0,8393	Нм = 0,26 мм ₽л/=29° г0 = 0,71 мм
Адвентиция	СА = 0,3 кПа кХА = 0,5620 кПа к2А =0,7112	Нм = 0,13 мм Рл/=62° г2 =1,1 мм

Так как все формулы и преобразования абсолютно идентичны для обоих слоев, индекс j в дальнейшем будем опускать.

Представив тензор напряжений Пиолы в виде разложения по двойному базису

D — D_rRQ_rQ_R + В_гфе _ге_ф + D_rZ6_re_z + Оф^СфС^ + 7)ффефеф

■^О^е^ф + DzRezeR + DzOe2eo + DzZezez, уравнения равновесия v преобразуем к следующей скалярной форме, dDR dD zR ^rR ^^Ф p. a or oz        r

<Ф_гф 1 дВ^ф 5В₂ф D^r - В_гф ,

--1----1---1--- dr r d(p dz         r

^+l^^tlD,z=0.

dr r d(p dz r

Эти уравнения следует дополнить граничными условиями на внешней и внутренней поверхностях сосуда.

Действие на внутренней поверхности сосуда кровеносного давления эквивалентно приложенной распределенной нормальной нагрузке. Соответствующее граничное условие представляется в виде

^'^д|

'Г = Гд где / - интенсивность давления на единицу площади деформированного тела.

Граничное условие на внешней поверхности представляет свойства околососудистой среды

=^№-1)

V г J

где к - безразмерный коэффициент, характеризующий свойства упругого основания. Из условия несжимаемости имеем

RW-Jno+Ar^-rd),                  (9)

V КЛ где R0=R(r0) - внутренний радиус сосуда после деформации.

Воспользуемся определяющими соотношениями вида [1]: dW 1

Р = 2—-pG-1,                      (10)

где р - функция гидростатического давления в несжимаемом материале, не определяемая через деформацию и являющаяся функцией только радиальной координаты г.

Из формы функции энергии (4), определяющих соотношений (10), формулы

D = P С,

(И)

и ограничений, наложенных на функцию р, следует, что компоненты тензора напряжений Пиолы, которые имеют вид

D_rR=^-^—pG;^R', V °G_rr )

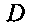
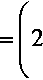
dW

dW

^G^

"PG^

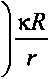
SIT dG_zz

-pG^ R\y, J

0^2 =

SW

dG(pZ

-pG^

К

^ 6W

< 5GZZ

"PG^ X, )

являются функциями только координаты г.

Поэтому два из трех уравнений равновесия удовлетворяются тождественно, а третье принимает вид:

^dDrR ,^DrR ^фФ _D _q

—-— +--V £>2ф - и dr г

Из решения системы, включающей в себя краевую задачу dDrR , DrR "^ФФ D _0 —— +--V и2Ф - и= dr г

(14.1)

П»   -_Ск^ 1)

urR     ~ ^Ак--1

Г = Г1        V Г )r = r. ■ и граничное условие на внутренней поверхности

R'D^ = -f,                         (14.2)

r = r0

находятся внутренний радиус цилиндра в деформированном состоянии R_o и функция гидростатического давления в несжимаемом материале p^Y Функции Dy^rY входящие в уравнение, являются кусочно-непрерывными функциями вида

^•И =

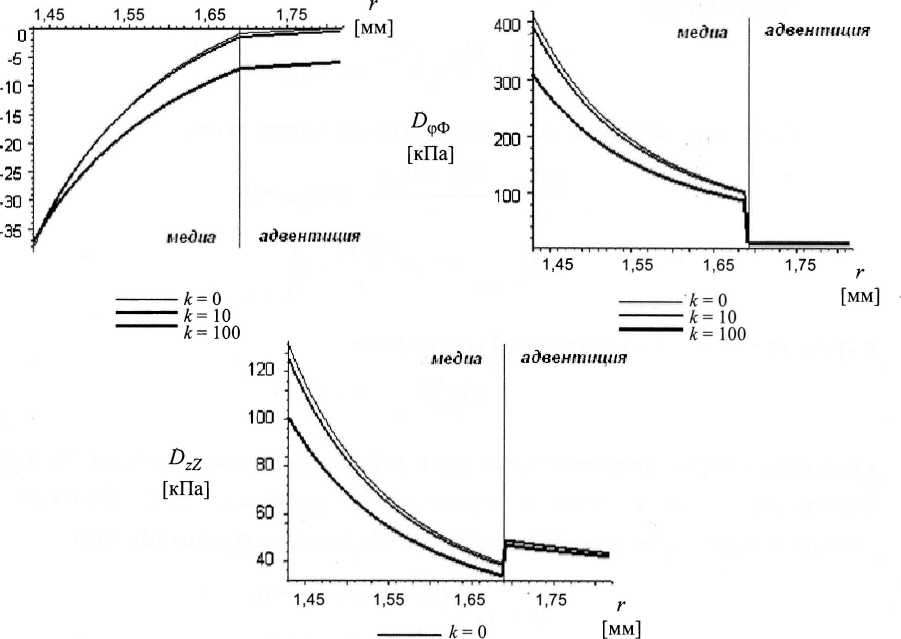
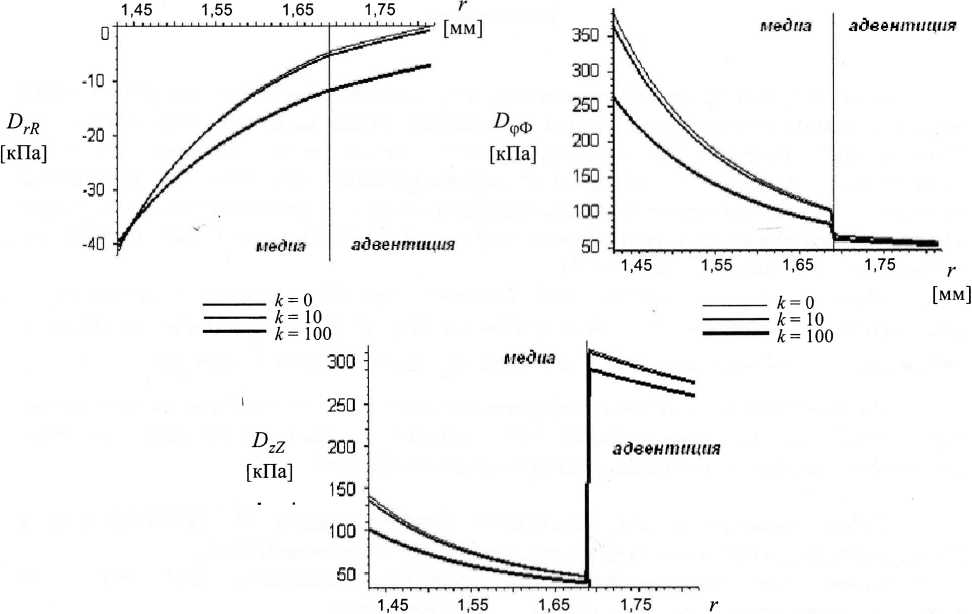
Dy

Физиологическое состояние сосуда характеризуется значениями параметров / = 13,33 кПа и Х = 1,7.

Результаты и обсуждение

Упругий материал, задаваемый функцией энергии (4), хотя и обладает винтовой анизотропией, не проявляет эффекта взаимодействия крутильных и радиальных деформаций. Это означает, что при у = 0 в цилиндре отсутствуют касательные напряжения D^, В_гф, D_zR, D_rZ. Таким образом, задача о раздувании и осевом растяжении цилиндра отделяется от задачи кручения. Кручение будет возникать, только если на его торцах действует крутящий момент.

Численное решение задачи проведено в отсутствии кручения цилиндра (у = 0). В результате получены графики распределения нормальных напряжений для различных значений параметра нагружения X и коэффициента к (рис.2, 3).

Анализ качественных различий в распределении напряжений для различных X показывает, что в окрестности физиологического состояния основной вклад в механические свойства стенки сосуда вносит медиа. При увеличении растяжения становится более существенным вклад адвентиции. Причем упругие свойства адвентиции оказывают более заметное влияние на напряжение D_zZ, чем на два других. При X = 1,9 максимум D_zZ в адвентиции превосходит максимум в медиа примерно в два раза. Таким образом, можно сказать, что внешний слой сосуда предохраняет его от разрыва при растяжении. Это полностью соответствует данным, полученным опытным путем [7, 8].

^rR [кПа]

цилиндра для различных к = 10

к = 100

Рис. 2. Распределение нормальных напряжений по радиусу значений коэффициента к при X = 1,7

—к-0     I¹™¹

-------к = 10

-------к = 100

Рис. 3. Распределение

нормальных напряжений по радиусу цилиндра для различных значений коэффициента к при X = 1,9

Таблица 2

Уменьшение напряжений во внутренней стенке сосуда в процентном отношении к состоянию к =0 _________________(абсолютные величины)_________________

		X = l,7	X = l,8	X = l,9
£=10	D,r	2,22	0,12	1,6
	D фф	4,85	2,43	4,66
	DzZ	4,44	2,22	4,24
£=100	D,r	2,76	1,37	3,76
	°ФФ	25,36	25,07	31,05
	DzZ	23,34	23,04	28,45
£=200	DrR	3,51	5,5	8,384
	D A фф	50,64	56,25	66,34
	DzZ	46,9	52,26	61,68

Заключение

Известно, что причиной разрушения внутренней поверхности сосуда, а также возникновения атеросклероза является повышение уровня напряжений во внутреннем слое стенки сосуда. Представляет интерес исследовать влияние жесткости околососудистой среды на напряженно-деформированное состояние во внутренней стенке сосуда. Из сравнения значений напряжений видно, что учет влияния внешней упругой среды приводит к уменьшению расчетных значений нормальных напряжений во внутренней стенке сосуда (табл. 2).

Можно также отметить, что наличие упругого основания приводит к увеличению значений радиальной компоненты D_rR во внешней стенке сосуда, в то время как значения окружной Р и осевой D_zZ компонент уменьшаются.

Изучив влияние величины коэффициента жесткости внешней среды на значение напряжений, можно сделать вывод, что значения к, соответствующие свойствам реальной околососудистой среды, лежат в интервале (8, 120).

Работа выполнена при поддержке РФФИ, проект № 05-01-00638-а и Международного совета по научным исследованиям и обменам (IREX).

Автор выражает сердечную благодарность профессору Л.М. Зубову за пристальное внимание к работе и помощь в ее выполнении.