Влияние особенностей конструкционного демпфирования на нелинейные колебания виброзащитных систем
Автор: Лазуткин Г.В., Антипов В.А., Рябков А.Л.
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Механика и машиностроение
Статья в выпуске: 3-1 т.11, 2009 года.
Бесплатный доступ
Решается задача о простейшей форме аппроксимации деформационных характеристик виброзащитных устройств с конструкционным гистерезисом на основе минимизации среднеквадратичной погрешности приближения, а также равенства площадей приближаемых петель гистерезиса к искомым. С помощью комбинированного асимптотического метода разложений решения нелинейного дифференциального уравнения движения виброзащитных систем и предложенной формой аппроксимации отыскивается решение для квазигармонических колебаний, учитывающее влияние особенностей конструкционного гистерезиса виброизолирующих и демпфирующих устройств на основные параметры колебаний.
Виброзащитные системы, гистерезис, аппроксимация, уравнение движения, квази-гармонические колебания
Короткий адрес: https://sciup.org/148198613
IDR: 148198613 | УДК: 620.318.6
Текст научной статьи Влияние особенностей конструкционного демпфирования на нелинейные колебания виброзащитных систем
Рябков Алексей Леонидович аспирант случае, нелинейную геометрическую форму. Указанные обстоятельства позволяют выявить вид основных определяющих критериев подобия и с помощью методов теории подобия и анализа размерностей экспериментально определить обобщенные деформационные характеристики (УГХ) для изучаемого класса СКД.
Обычно УГХ устройств получают при их циклическом деформировании. Найденные при этом семейства петель гистерезиса преобразуют к обобщенному (безразмерному) виду с помощью афинных преобразований координат нагрузка-деформация. Причем для описания процессов деформирования произвольного нагружения СКД, свойственного переходным процессом неустановившихся колебаний ВС, определяют виды нелинейных преобразований процессов нагрузки и разгрузки петель гистерезиса, а также условия их сшивки в точках смены знака скорости деформации [2, 3]. При наличии полученных таким образом данных об УГХ устройств несложно получить известными численными методами (Рунге-Кутта и др.) решение дифференциального уравнения движения ВС, обладающее свойством точного. Последнее особенно важно при проведении поверочных расчетов динамических характеристик ВС.
Заметим, что при гармоническом возбуждении ВС переходные процессы неустановивших-ся колебаний, благодаря высокой степени конструкционного демпфирования, быстро затухают, а установившиеся в дальнейшем колебания определяются особенностями циклического деформирования СКД. Следовательно, при теоретическом исследовании квазигармонических установившихся колебаний ВС можно воспользоваться математическим описанием семейств петель ги- стерезиса СКД. Оно должно достаточно полно и просто отображать важнейшие особенности УДХ устройств, связанные с нелинейностью их упругих и неупругих составляющих.
Представим описание контуров симметричных петель гистерезиса суммой двух функцией:
Ф(s, х, А) = Фу( х, А) + Фm(s, х, А), (1) где X, X , А — соответственно, скорость, перемещение (деформация) и ее амплитуда;
Фу=0,5(Ф1 + Ф2);Фm=0,5(Ф1- Ф2) - соответственно условные упругая и неупругая составляющие реакции СКД – R = Ф(s, х, А);
Ф1, Ф2 - функции, описывающие процессы нагрузки ( X > 0) и разгрузки ( X < 0) соответственно;
с г = signx - ступенчатая функция, определяемая знаком скорости.
Воспользовавшись результатами анализа работ [2, 3, 4], отметим главные особенности поведения УГХ для различных СКД, выполненных на основе материала МР, тросов, многослойных пластин и т.п.:
-
- нелинейность функций Фу и Фm в наибольшей степени проявляется на концах отрезков х е [ - А , А ] , где коэффициенты жесткости могут изменяться в десятки и сотни раз;
-
- форма неупругой составляющей Фm (гистерезисной функции) в зависимости от амплитуды деформации А может быть близкой как к эллипсу, так и к параллелограмму с вертикальными стенками, характерному для сухого трения;
-
- упругая и неупругая составляющие имеющие сдвиг по фазе, между собой, равный п /2 .
Как показано в работе [2], аппроксимация упругой составляющей реакции СКД ортогональными полиномами Чебышева обеспечивает наилучшее приближение на концах отрезка х е Г - А , А ] , в связи с чем запишем:
изменение жесткости в окрестности значений деформации х = А.
Таким образом можно записать:
Ф
m
= с T ( A ) + P m ( A ) A
- x 2
В дальнейшем коэффициенты аппроксимации T(A), pm(A) и cq(А) будем записывать в виде Т, рm, cq, подразумевая при этом их функциональную зависимость от амплитуды А.
В дальнейшем коэффициенты аппроксимации T(A), pm(A) и cq(А) будем записывать в виде Т, рm, cq, подразумевая при этом их функциональную зависимость от амплитуды А.
Определим коэффициенты аппроксимации Т, р, m и вид весовой функции f ( x ) , где x = x / A , которые обеспечивали бы минимальную среднеквадратическую погрешность Q приближения
Q = ЛФ
- 1 1
- с
T + P m
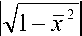
1 f ( x ) dx . (4)
d Q d Q
Найдем частные производные и и, dT dPm приравняв их к нулю, получим систему интегральных уравнений в виде:
i - f Ф„-
-1L
1Г f Ф m - ° [ T
, - 1 L ^
O T + Pm \ 1 - x 2 ) f ( x ) dx = 0;
- x 2 f ( x ) dx = 0. (5)
m
Ф у ( X , А ) « £ С ( A ) x q , q e [ 1,3.. m ] . (2) q = 1
Здесь Сq(A)– коэффициенты полиномов Чебышева степени q, функционально зависящие от амплитуды деформации А, причем для каждого класса СКД они могут быть представлены по переменной А полиномами или другими видами аппроксимирующих функций.
Выберем вид аппроксимации гистерезисной функции с учетом указанных выше особенностей ее поведения. Предварительно заметим, что в самом простейшем виде она должна содержать по крайней мере два члена, один из которых представляет прямоугольник с половинами сторон Т(А), А, а другой – эллипс с полуосями рm(A), А. Это обеспечивает сдвиг по фазе, равный п /2 , между упругой и неупругой составляющей реакции СКД, а также скачкообразное
Заметим, что при установившихся вынужденных колебаниях ВС работа возбуждающей нагрузки затрачивается на рассеяние энергии, определенной гистерезисной функцией. Следовательно, при выборе весовой функции f ( x ) требуется учитывать необходимое условие равенства площадей искомых и приближаемых к ним петель гистерезиса, которое можно записать в виде:
f
Ф m
- O T + Pm
v
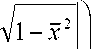
dx = 0.
Разрешая с этим уравнением систему интегральных уравнений (5), получим два вида весовой функции f ( x ) :
./ 1 (- x ) = 1 ; f , < x ) = ( -iv-P У1.
Тогда минимум функционала Q (4) в пространстве переменных T и pm определяется с помощью двух различных систем интегральных уравнений:
для f ( x ) =1,
Ф
m
<7 l T + p
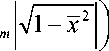
dx = 0;
-
Ф m
^1 T + Pm
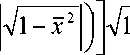
- x 2 dx = 0;
Для f , ( x ) = (V1 - x 2 ) 1 ,
1 2 dx
J Фm - ^1 T + Pm V1 - x I "T=-1L V /J 71 -
= 0;
где в cos ( to t + а ) - безразмерная возбуждающая нагрузка;
a - угол сдвига по фазе между возбуждающей нагрузкой и перемещением;
x , в , ® , t - безразмерные ускорение, амплитуда возбуждающей нагрузки, частота и время соответственно.
Отметим, что квазигармонические колебания ВС могут быть представлены разложением Фурье в виде:
J Фm - ^[ T + Pm V1 - x2
dx = 0.
х ( t ) = X a, cos u ot + B , sin u ot ,
Разрешая эти системы уравнений относительно коэффициентов аппроксимации T и pm,
i = 1
получим:
причем на характер закона движения при t=0 накладываются следующие ограничения:
Pm =
T =
8 - л1
8 - п 2
для случая f 2 ( x ) =
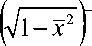
I
J Ф m ( c ,cos ^ , A ) 1—sin ^ I d ^
0 V 2 V
?^ пI
J Ф ( y ,cos ^ A ) sin V -- I d v , 0 V 4 /
где ф = arccos x .
Аналогично можно получить выражения и для коэффициентов аппроксимации T и pm при f ( x ) =1:
nn
X 4 = A ; X B / = 0; i e [ 1,3,5... n ]. (11)
i = 1 i = 1
Найдем решение уравнения движения (9) с помощью комбинированного асимптотического метода (КАМ), основывающегося на сочетании методов малого параметра с вариационными принципами. Согласно КАМ построение асимптотических разложений уравнения движения (9) осуществляют по степеням малого парамет-
<
P m = 6 П П Ф ^ cos V -^П ф 1 - -Sin v l dV, 3 п 2 - 32 0 V 71 V
T = ^6У Ф fc cos v .^п ф м ф - d (7) 3 п 2 - 32 0 V 3 ? /
ра ^ , 5 e1: x = X ^ x a ; А = X ^ A d , пу- d = 0 d = 0
Таким образом, с учетом выражений (2) и(3) реакция СКД, характеризуемая УГХ в виде семейства симметричных петель гистерезиса, может быть представлена в виде приближения:
тем искусственного введения в уравнение (9) дополнительных функций: для реакции СКД – Rл = g2х, а для возбуждающей нагрузки - Р л = P C0 c°s u t . Коэффициенты g2u Ьсо находят методом Бубнова – Гaлеркина, причем, как показано в работе [2], g2 является коэффициентом гармонической линеаризации по Чебышеву. Учитывая изложенное, преобразуем уравнение движения (9) к виду:
m
R = X с xq + ^ T +
q q = 1
V
p
m
A 2
-
x
Л
, (8)
/
x + у 2 x = X ^ d ( Ped cos u t + P sd sin u t ) + d = 0
где сq – коэффициенты полиномов Чебышева, для условной упругой составляющей реакции, а T и pm – коэффициенты аппроксимации для неупругой составляющей, найденные с помощью выражений (6) или (7). Следует помнить отличие этих коэффициентов на величину А, Аq для случая переменной x по сравнению с х .
Воспользуемся полученным выражением для реакции СКД (8), и запишем дифференциальное уравнение движения ВС для установившихся квазигармонических колебаний:
+ Б
m
Y2x -Xeqxq q=1
причем
в 2
m
г
х+ X с xq +о T+P
A 2 -
-
2
g
X
P
ed
V
d
=
0
/
-
x
2
, q q = 1
V
m
)
x
2
=
fl
co^
o
t
+
а
), (9)
/
2
g
X
P
sd
V
d
=
0
/
gg tga = X Psd I X Ped. (14)
d
=
0
d
=
0
Ограничим q=1, m=3 и заметим, что по методу КАМ для уравнения (12)
в
sо= 0. Представим уравнение движения (12) в виде системы линейных дифференциальных уравнений по степеням порядка приближения
^
d
:
e
o
x
0
+
у
2
x
0
=
P
c
0
cos
to
t
;
(15)
x
1
+
у
2
x
1
=
в
с 1
cos
to
t
+
P
si
sin
to
t
+
у
2
x
0
-
e
1
-
E
c
q
x
0 q
=
1
-
^
T
+
p
m
[л/
A
0
-
x
0 P
ные гармоники квазигармонических колебаний (11), определим амплитуды гармоник возбуждающей нагрузки:
P
c
0
=
A
0
(
Y
2
-
to
2);
при этом x = x 0 + X1. Порождающее решение уравнения (15) имеет гармоническую форму:
x
0
=
A
0
cos
to
t
,
(18)
где О Л 4T^ YY
P
s
1
=
p
m
A
0
+
/ - 9
П
i
=
1
Y
- -
A
o
=
P
c
o
. Y - to С учетом решения (18) представим неупругую составляющую реакции СКД, входящую в уравнение (16), в виде гармонического разложения:
of
T
+
p
a]
A
—
x
2 I =
V m 7
4
T
n
1
— V- sin
i
to
t
+
А
0
p
m
sin
to
.
n
i
=
1
i
В силу гармонической формы решения(18) и выбора для аппроксимации упругой составляющей реакции СКД (в том числе и дополнительной функции Rл) полиномов Чебышева, получим [2]:
Y
2
x^
— -^
Cqx
q
=
— C
3
A
3 cos3
to
t
.
~ q
4
Тогда уравнение (16) приобретает следующий вид:
x
+
Y
2
x
1
=
P
C
1
cos
to
t
-
4
с
3
А
03 cos3
to
t
+
4
T
4
T n
1
+ (P -PmA0--)sintot--E"sinitot• n n i=3 i Чтобы обеспечить в порождающем решении (18) выбор полной амплитуды первой гармоники, потребуем отсутствия в поправочном слага- емом х1 членов, содержащих косинусы, следовательно, bС1 = 0. Нахождение частного решения преобразованного вышеуказанным образом линейного дифференциального уравнения (16) не представляет затруднений и закон квазигармонических колебаний ВС (17) может быть представлен в следующем виде: x (' ) =
P
c
0
2 2 Y - to
cos
to
t
-
c
3
A
0
3
4(
Y
2
-
9
to
2)
cos
3
to
t
+
P
s
1
-
P
m
A
0
-—
4
T
n
1
(20)
+-----------
——
sin
to
t
--V -----
—-г sin
i
to
t
•
Y - to n
i
=
3
i
(
y
2
-
i
2
to
2
)
Сопоставляя его с полученным выражением (19) и, учитывая ограничения на синусоидаль-
to
2
. i to С учетом выражений (11), (13), (14) окончательно можно записать <
2 2\2 I
л
4T
Y - to
I ,,2
A
0 (
Y
-
to
) +|
P
m
A
0 + —
-
2 -2 2
I =
P
;
V
П
~=r
Y
-
i
to
)
p
m
4
T n
1
tg
a
=2 2+^V2 -2 2 ;
Y
-
to n
A0
*=1
y
-
i
to
pm
A
=
Ac
^
A
0___ 0
4(
y2
-
9
to
2)
. Решения данной системы уравнений является основой для исследования влияния форм петель гистерезиса СКД и параметров возбуждения на характер квазигармонических колебаний ВС. При этом полученный закон колебаний ВС (20) вместе с системой уравнений (21) позволяет определить интенсивность гармонических составляющих и особенности поведения динамических характеристик: зависимости коэффициентов передачи и резонансных частот ВС от амплитуды возбуждающей нагрузки, затягивание резонансных режимов и т.п.
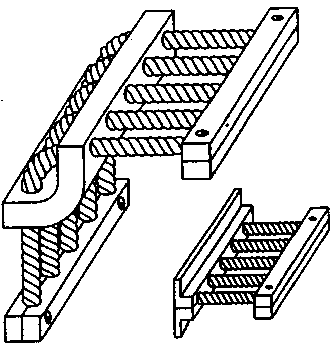
В качестве примера рассмотрим применения полученных результатов (см. выражения (20) и (21)) для исследования нелинейных колебаний ВС, в состав которых могут входить многослойные пластинчатые упругодемпфирующие опоры (УДО), тросовые виброизоляторы (рис. 1
а,б
) [4]. УДО (см. рис. 1,
а
) состоит из двух пакетов многослойных пластин (1), прижатых друг к другу пружинной скобой (2). Тросовые виброизоляторы могут быть Г–образного типа или в виде гребенки с прямолинейными участками отрезков тросов (рис. 1,
б
).
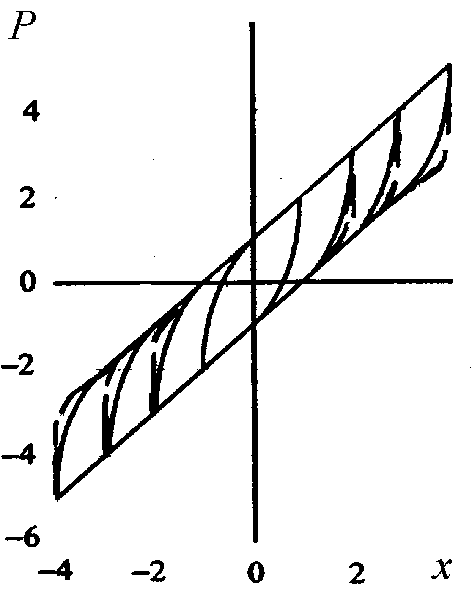
На рис. 2 представлены обобщенные поля петель гистерезиса СКД [4] (вышеуказанных УДО и тросовых виброизоляторов). Выделяя из представленных петель гистерезиса СКД упругие и неупругие составляющие (гистерезисные функции) (1) и вычисляя значения для коэффициентов
Cq
(
A
) и
Рm
(А), Т(А) при различных
А
е
[0,2;6,0] с помощью выражения (6) найдем значения вышеуказанных коэффициентов.
Анализируя полученные данные замечаем, что для больших амплитуд деформация
Ар
>2 свойственных резонансным режимам колебаний ВС, можно отметить, что значение величины
ртA
<<
T
<<1. Вследствие этого для амплитуд
А
>2
а) б)
Рис. 1.
Системы конструкционного демпфирования:
а
) – УДО;
б
) – тросовые виброизоляторы
Рис. 2.
Обобщенное поле упругогистерезисных петель: ––– тросовых виброизоляторов с прямолинейными упругогистерезиными элементами; – – – УДО
тема уравнений (22) отображает приближенное решение для ВС с сухим трением, причем точное решение получено в работе [5] и может быть представлено в безразмерном виде:
, I
в
2 1
ГП"
Ao
=
Мл 2\2
2 tg
о . (24) у (1
-to
2
)
2
to
2to v 7
Сравнение точного решения (24) с приближенным (22) показывает, что при исследовании колебаний ВС с высокой степенью конструкционного демпфирования крайне важно учитывать достаточно большое количество гармонических составляющих
Ai
(23). При этом погрешность определения амплитуды ВС по сравнению с точным зависит не только от числа учитываемых гармоник в решении (22), но и значений b. При
можно считать
p
m
—
0. Вместе с тем оказывается, что при
А
>2 величина
С
3
А
3<<
С
1
А
(
q
е
[1,3] см. выражение (2)), что позволяет считать
С
3 0,
С
1
=1.
-
Тогда система уравнений (21) для значений амплитуд
А
>2 приобретает следующий вид
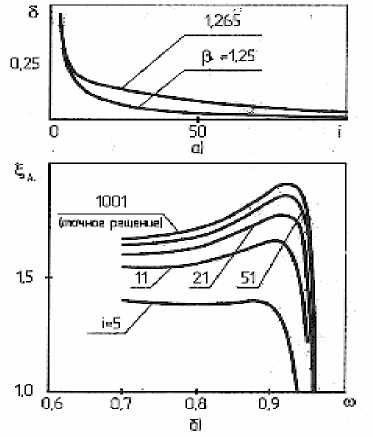
увеличении b до значений близких к Р = _ по грешности могут достигать до 30 % и более в зависимости от числа учитываемых гармоник. На рис. 3 представлена зависимость коэффициента A передачи ^ = р от безразмерной частоты to для
A
02
(1
-™
2
)
2
+ - L
П
i
=
1
1
-to
2
1
-
i
2
to
= К
2
;
4T n tg a = —L
П
A
0
i
=
1
A
=
A
о
-
;
1
-
i
2
to
2
При этом высшие гармонические составляющие
Ai
квазигармонических колебаний вычисляются с помощью выражения (20) по формуле
4
T n
1
i
.
n
7=3
1
(1
-
i
to
)
Заметим, что в этом случае полученная сис-
различного числа учитываемых гармоник (рис 3,б) при b=1,25. На рис. 3,
а
приведены значения погрешностей
§
приближенного решения (22) по сравнению с точным (24) в зависимости от числа учитываемых гармоник
i
и уровня возбуждающей нагрузки b.
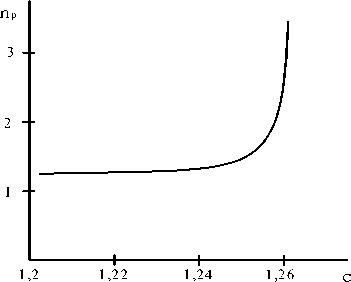
На рис. 4 представлена зависимость Коэффициентов передачи на резонансе
^
р
=
A
- (
А
р
-амплитуда резонансных колебаний ВС) о
p
т уровня возбуждения при учете
i
=1001.
Как видно из приведенных данных коэффициент передачи на резонансных режимах работы виброизоляторов и демпферов с конструкционным демпфированием существенно зависит от уровня возбуждения и может изменяться от значений 1,2 до 5–10 и более. Причем, начиная с
в >
1.265
, интенсивность изменения коэффи-
Рис. 3.
Сравнение точного решения для сухого трения с приближенным:
a
– погрешность приближенного решения в зависимости от числа гармоник и уровня возбуждения,
в
0
е
[
1,25;1.265
]
б
– характер влияния числа гармоник, учитываемых в приближенном решении,
в
0
=
1-25
Рис. 4.
Зависимость коэффициента передачи на резонансе от уровня возбуждения
Таким образом, предложенные в работе подходы к описанию УГХ виброизоляторов и демпферов с сухим трением, а также метод решения нелинейных дифференциальных уравнений движения ВС позволяют с высокой степенью достоверности изучать влияние особенностей конструкционного демпфирования на нелинейные колебания систем виброзащиты.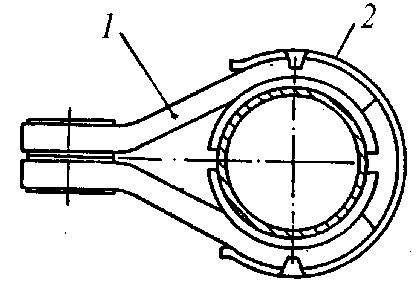
Список литературы Влияние особенностей конструкционного демпфирования на нелинейные колебания виброзащитных систем
- Лазуткин Г.В. Вынужденные периодические колебания виброзащитных систем с конструкционным гистерезисом. Вибрационная прочность и надежность двигателей и систем летательных аппаратов. Куйбышев: КуАИ, 1986, с. 81-86.
- Лазуткин Г.В. Виброизоляторы из материала МР (тип ДКУ). Деп. в ВИНИТИ -№1977 -85 от 19.03.85. -б/о №771, библ. указ. №7 -22 с.
- Расчет и конструирование средств виброзащиты сухого трения/В.А. Антипов, Ю.К. Пономарев, А.И. Белоусов, и др. -Самара: СамГАПС, 2005. -207 с.
- Чегодаев Д.Е., Пономарев Ю.К. Демпфирование. -Самара: Издательство СГАУ. 1997 -334 с.: ил.
- Быховский И.И. Основы теории вибрационной техники/И.И. Быховский. -М.: Машиностроение, 1968. -362 с.


