Влияние параметра b солнечного ветра на статистические характеристики Ap-индекса в цикле солнечной активности

Магнитосфера представляет собой сложную динамическую систему, постоянно подверженную воздействию плазмы солнечного ветра (CВ) и межпланетного магнитного поля (ММП). Многочисленные исследования, например [Burlaga, 1991; Marsch, Tu, 1997; Рязанцева, Застенкер, 2008; Yordanova et al., 2009] , показали, что параметры потока плазмы СВ имеют перемежающийся характер. Так, функции распределения скорости и магнитного поля СВ демонстрируют негауссову природу [Marsch, Tu, 1997] . Перемежающиеся флуктуации солнечного ветра оказывают существенное влияние на геомагнитную активность [Vӧrӧs et al., 2002; D’Amicis et al., 2010] . В работе [Yordanova et al., 2009] показано, что плазма СВ обладает турбулентными свойствами. Согласно [Borovsky, Funsten, 2003] турбулентность является характерной чертой не только плазменных потоков, но и магнитного поля в плазменном слое магнитосферы Земли. Таким образом, самой магнитосфере, активность которой определяется взаимодействием с СВ, свойственны перемежаемость и турбулентность.

Для характеристики магнитосферной активности традиционно используют планетарные геомагнитные индексы — например, A p -индекс. Считается, что A _p-индекс отражает влияние солнечной активности и межпланетной среды на состояние магнитосферы. При этом 11-летняя периодичность геомагнитной активности строго следует за 11-летним циклом солнечной активности [Schreiber, 1998] . Однако в отличие от солнечного цикла для периодичности геомагнитной активности характерны два максимума, один из которых наблюдается вблизи максимума солнечной активности, другой — на фазе ее спада [Schreiber, 1998] . Первый максимум в годовой динамике A _p-индекса связывают со спорадической солнечной активностью, к которой относят среди прочего корональные выбросы массы. Второй максимум обусловлен рекуррентной солнечной активностью, определяемой 27-дневным синодическим периодом вращения Солнца. Источниками рекуррентности геомагнитной активности являются высокоскоростные потоки из корональных дыр [Webb et al., 2001] .

Спектральный анализ Ар-индекса, выполненный в работе [Зотов, Клайн, 2017], позволил обнаружить эффект чередования двух режимов в динамике магнитосферы в каждом из 11-летних циклов солнечной активности. Один из режимов, условно названный авторами периодическим, характеризуется слабым широкополосным шумом с доминированием 27-дневной периодичности и ее нескольких гармоник. Для другого режима — хаотического — типично преобладание сильного широкополосного шума и практическое отсутствие 27-дневной периодичности. Надо отметить, что переходы от одного режима в динамике магнитосферы к другому достаточно резки. Такое поведение активности магнитосферы с резкими переходами от одного состояния к другому было названо триггерным режимом в динамике магнитосферы [Зотов, Клайн, 2017].

Дальнейшие исследования [Зотов и др., 2018] показали, что наиболее вероятным параметром, ответственным за чередование периодического и хаотического режимов активности магнитосферы, по-видимому, является параметр β СВ, равный отношению теплового давления к магнитному: β= NkT /( B ²/8π), где N и T — плотность [см^–3] и температура [K] плазмы протонов СВ, B — величина межпланетного магнитного поля [нТл]. Для динамического спектра параметра β, так же как и для спектра А р -индекса, характерно чередование двух режимов, разных по интенсивности шумового сигнала. Более того, мы обратили внимание на тот факт, что смена режима в динамике магнитосферы зависит от величины параметра β. При значениях β~1 в магнитосфере наблюдался хаотический, а при β>1 — периодический режим. Однако в предыдущей работе [Зотов и др., 2018] мы не анализировали влияние параметра β на характеристики геомагнитной активности ( А р -индекса) для периодического и хаотического режимов магнитосферы.

Настоящая работа является продолжением исследований [Зотов, Клайн, 2017; Зотов и др., 2018] и посвящена изучению влияния параметра β СВ на статистические характеристики А р -индекса, отражающего обнаруженный ранее эффект триггерного поведения активности магнитосферы.

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ

В настоящей работе в качестве характеристики солнечной и магнитосферной активности использованы среднесуточные значения чисел Вольфа (W) и Aр-индекса, полученные из Мирового центра данных по солнечно-земной физике (Москва) [] и Мирового центра данных в Киото [http://swdcwww. ] соответственно, за период с 1932 по 2018 г. Кроме того, использовались суточные и 27-дневные данные о параметрах плазмы СВ и ММП за 1964–2018 гг., представленные в базе данных OMNI [ ].

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Прежде чем анализировать влияние параметра β СВ на статистические характеристики Ар-индекса, необходимо кратко остановиться на особенностях активности магнитосферы в цикле солнечной активности, обнаруженных ранее. Приведем два рисунка [Зотов и др., 2018], которые отражают суть триггерного эффекта в динамике магнитосферы. По сравне- нию с работой [Зотов и др., 2018] в настоящей статье используется значительно больший объем данных (по 2018 г. включительно). Так, на рис. 1 показаны среднегодовая вариация числа солнечных пятен W, динамика среднегодовой амплитуды и спектральная плотность Ар-индекса с конца 16-го по 24-й цикл солнечной активности. Динамика амплитуды Ар-индекса отражает известные закономерности геомагнитной возмущенности, а именно: в каждом цикле солнечной активности наблюдаются два максимума, один из которых приходится на фазу роста или максимума, другой — на фазу спада цикла (рис. 1, а). На динамическом спектре Ар-индекса (рис. 1, б) явно видны резкие переходы возмущен-ности магнитосферы от периодического режима к хаотическому. Подобные переходы впервые были обнаружены в работе [Зотов, Клайн, 2017] на временном интервале 1932‒2000 гг. и названы триггерным режимом в динамике магнитосферы.

Рисунок 2, на котором представлены динамические спектры числа солнечных пятен W , А _р-индекса и параметра β с 20-го по 24-й цикл солнечной активности, наглядно демонстрирует, что одним из факторов, ответственных за эффект переключения режима в динамике магнитосферы, может быть параметр β СВ. Спектральная плотность чисел Вольфа имеет максимальную интенсивность и проявляет 27-дневную периодичность в максимуме каждого солнечного цикла (рис. 2, а ), явно не совпадающую по времени с периодическими режимами в динамике А р -индекса (рис. 2, б ). Следовательно, динамика числа солнечных пятен не связана с триггерным режимом активности магнитосферы. Для динамического спектра β-параметра характерны чередования широкополосного шума различной интенсивности (рис. 2, в ). Иными словами, в спектре параметра β четко видны резкие смены интенсивности хаотического режима, которые в основном совпадают по времени с переходами от периодического режима к хаотическому в спектре А р -индекса (рис. 2, б ). Следует отметить, что для динамических спектров других параметров СВ и ММП подобных особенностей не было выявлено. Временное совпадение смены характера спектров А _р-индекса и параметра β в цикле солнечной активности позволило нам предположить, что триггерный режим в вариациях А _р-индекса и, соответственно, магнитосферная активность управляются динамикой параметра β [Зотов и др., 2018] . Из сравнения динамического спектра А _р-индекса и среднегодовой динамики параметра β (рис. 2, г ) видно, что при значениях β~1 в магнитосфере наблюдается в основном хаотический режим, при β˃>1 — периодический.

В работе [Zotov et al., 2008] для периода 1932‒ 2000 гг. было показано, что распределение Ар-индекса имеет негауссову форму и для него характерен длинный хвост. Подобные распределения называют распределениями с тяжелыми хвостами (heavy tails или fat tails) [Малинецкий, Потапов, 2000]. Следовательно, закономерности распределения Ар-индекса аналогичны тем, которые характерны для перемежающихся процессов. В связи с тем, что в магнитосферной активности выделяются, по крайней мере, два режима — периодический и хаотический — возникают вопросы: 1) свойственна ли перемежаемость поведению Ар-индекса в каждом из выше рассмотренных режимов в динамике магнитосферы; 2) влияет ли параметр β СВ на статистические характеристики Ар-индекса для периодического и хаотического режима?

Для ответов на эти вопросы данные по А р -индексу были разбиты на две группы в соответствии с обнаруженными периодическим и хаотическим режимами активности магнитосферы. На рис. 3 приведены распределения амплитуд А _р-индекса N ( A _p) отдельно для интервалов периодичности ( а ) и хаоса ( б ). Видно, что для обоих распределений характерно плавное убывание числа суточных значений А р -индекса по мере роста их амплитуд, т. е. они имеют типичную форму распределений с тяжелыми хвостами. Согласно [Малинецкий, Потапов, 2000] подобные распределения удовлетворительно аппроксимируются степенными функциями вида f ( x )= x ^{– α} при x , превышающем некоторое пороговое значение x 0 . При этом не обязательно, чтобы все распределение аппроксимировалось степенной функцией, достаточно, чтобы это условие выполнялось при x > x 0 . На этом же рисунке показаны кумулятивные функции распределений А _р-индекса P ( A _p) и аппроксимации их хвостов степенными функциями вида P ( A p )=( А р )^{– α} . Методика получения кумулятивной функции распределения амплитуд сигналов и показателя степени α , характеризующего наклон кумулятивной функции распределения А р -индекса, достаточно подробно изложена в работе [Куражковская, Клайн, 2015] . Из рис. 3 следует, что, независимо от типа режима активности магнитосферы, хвосты кумулятивных функций распределений амплитуд А р -индекса довольно хорошо аппроксимируются степенными функциями, но значения α существенно различаются для периодического и хаотического режима: α =3.79 и α =2.90 соответственно. Степенной закон распределения амплитуд А _р-индекса для обоих режимов в динамике магнитосферы свидетельствует о перемежаемости и связанной с ней турбулентности магнитосферной активности. По величине показателя α можно на качественном уровне судить о степени турбулентности магнитосферы в периодическом и хаотическом режимах.

На рис. 4 представлены усредненные спектры мощности суточных значений А р -индекса для периодического и хаотического режимов. Построение спектров мощности основано на преобразовании Фурье. Значения А р -индекса разделялись на временные интервалы (в соответствии с делением на периодический и хаотический режимы), для каждого из которых был построен спектр мощности. Затем все спектры А р -индекса для режимов каждого типа усреднялись. Полученные спектры для обоих режимов хорошо аппроксимируются экспоненциальными функциями:

S(f)∼exр(‒γ f), где S — спектральная плотность; f — частота; γ — показатель, характеризующий наклон спектра. Показатели наклона спектра Ар-индекса для разных ре-

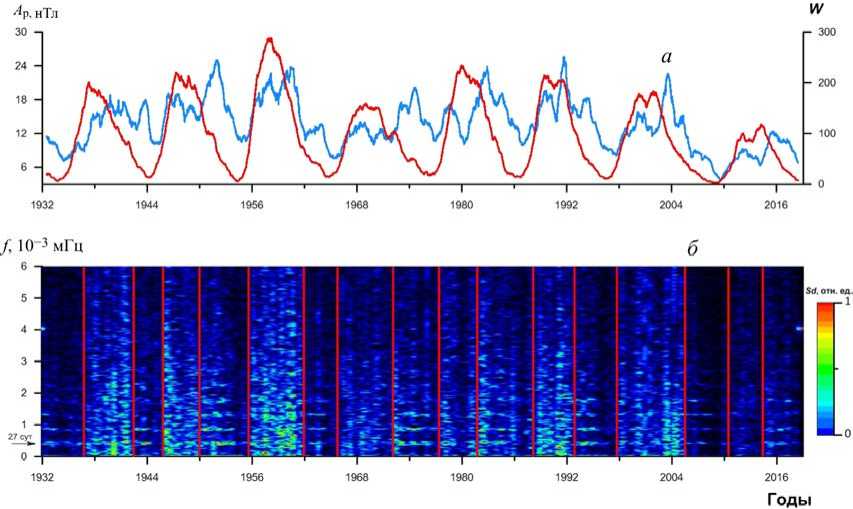
Рис. 1. Среднегодовые вариации числа солнечных пятен W (красная кривая) и А _р-индекса (голубая кривая) ( а ), а также динамический спектр А _р-индекса с конца 16-го по 24-й цикл солнечной активности ( б ). Вертикальными линиями обозначены границы периодических и хаотических режимов

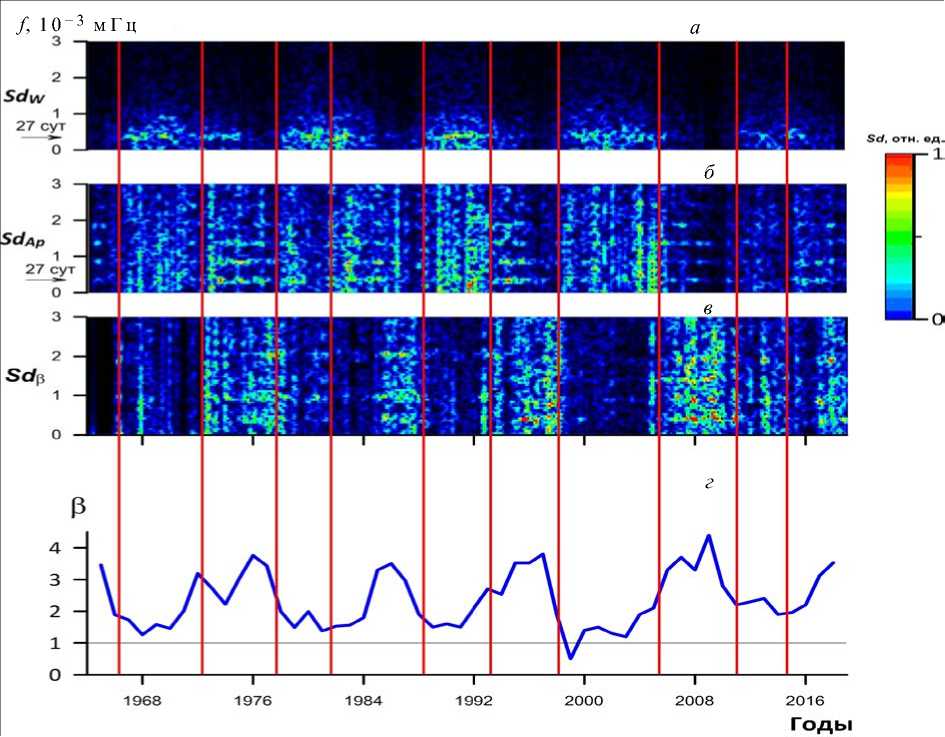
Рис. 2. Динамические спектры: числа солнечных пятен W — Sd_W (а ); А _р-индекса — SdA _p ( б ); параметра в — Sd в ( в ); а также среднегодовая динамика параметра в ( г ) в 20-24-м циклах солнечной активности. Вертикальными линиями обозначены границы периодических и хаотических режимов

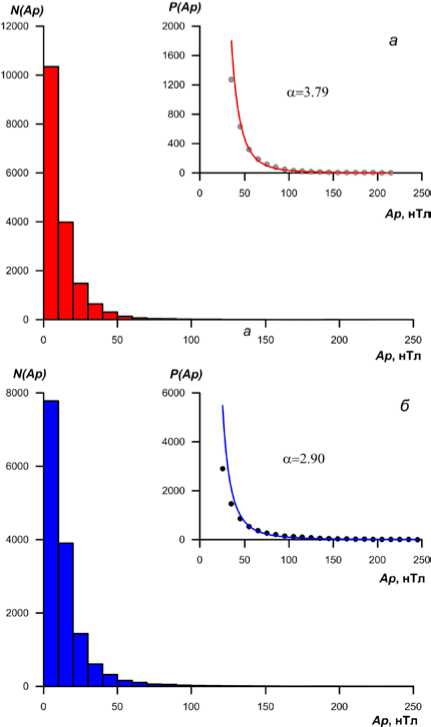
Рис. 3. Распределения N(А _р) суточных амплитуд индекса А _р для периодического ( а ) и хаотического ( б ) режимов в динамике магнитосферы в 1932-2018 гг. Справа приведены аппроксимации «хвостов» кумулятивных функций распределений P(A _p) амплитуд А _р-индекса (кружки) степенными функциями (сплошная линия)

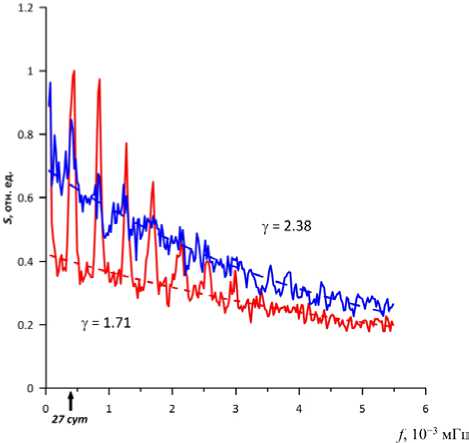
Рис. 4. Спектры мощности суточных значений индекса А _р для периодического (красная кривая) и хаотического (синяя кривая) режимов в динамике магнитосферы в 1932-2018 гг. Штриховыми линиями показаны аппроксимации спектров А _р-индекса экспоненциальными функциями

жимов различаются: y =1.71 и y =2.38 для периодического и хаотического режимов соответственно. Таким образом, с точки зрения статистических свойств А р -индекса в режимах активности магнитосферы наблюдаются как общие черты, так и различия. Общие черты заключаются в том, что перемежаемость магнитосферной активности свойственна как для периодического, так и хаотического режима. Различия показателей степеней аппроксимирующих функций указывают на разные уровни турбулентности магнитосферы в каждом из режимов, появление которых зависит от величины параметра в.

На рис. 5 приведены зависимости средних значений А р -индекса от параметра в СВ для периодического и хаотического режимов. При построении этих графиков использовались суточные значения А р -индекса и параметра в. Из анализа исключались значения А _р-индекса, для которых были пробелы в данных параметра в. Необходимо отметить, что в-па-раметр изменяется в основном от ~ 0.1 до ~ 4.0. Согласно [Веселовский и др., 2010] в этот диапазон изменения в-параметра попадает около 90 % всех наблюдаемых значений. Поэтому на рис. 5 мы привели зависимости средних значений А р -индекса от параметра в при 0 < в < 4 для обоих режимов активности магнитосферы. Средние значения А _р-индекса определялись следующим образом. Первоначально по исходным данным вычислялись скользящие средние по 50 точкам. Затем проводилась сплайн-аппроксимация полученных данных. На рис. 5 видно, что наибольших значений А _р-индекс достигает при в~1 в случае как периодического, так и хаотического режима. Вместе с тем максимум А _р-индекса для хаотического режима приходится на значения β<1, а для периодического — на значения в>1. Полученные различия зависимостей А _р(в) статистически значимы. При в >> 1 А p -индекс постепенно уменьшается с увеличением в. Зависимости А _р(в) для периодического и хаотического режимов имеют явно нелинейный характер, что свидетельствует о нелинейном поведении возмущенности магнитосферы, характеризуемой А _р-индексом.

На рис. 6 приведены гистограммы, отражающие энергию флуктуаций А р -индекса для периодического и хаотического режимов активности магнитосферы с конца 16-го по 24-й цикл. Энергия флуктуаций А _р-индекса рассчитывалась умножением средней амплитуды спектральной плотности на ширину спектральной полосы. Видно, что практически в каждом цикле солнечной активности энергия флуктуаций А _р-индекса для хаотического режима выше, чем для периодического. Исключение составляют 20-й цикл солнечной активности, в котором энергии флуктуаций А _р-индекса для периодического и хаотического режимов сравнимы по величине, и незавершенный 24-й цикл. Различие между энергией флуктуаций А р -индекса для периодического и хаотического режима статистически значимо. Это следует из оценок ошибок определения энергии на уровне 95 %, которые обозначены на рис. 6 вертикальными

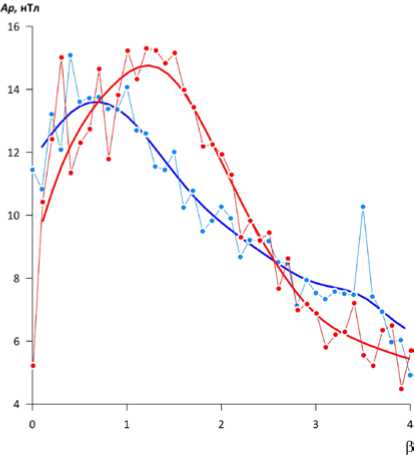
Рис. 5. Зависимости А _р-индекса от β СВ для периодического (красные кружки) и хаотического (голубые кружки) режимов для 1965–2018 гг. Сплайн-аппроксимации экспериментальных данных для периодического и хаотического режимов показаны красной и синей кривыми соответственно

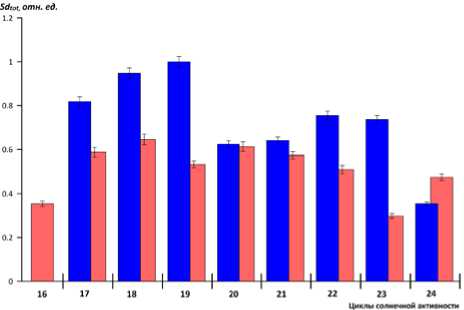
Рис. 6. Энергия флуктуаций Ар-индекса (Sdtot) для периодического (красный цвет) и хаотического (синий цвет) режимов с конца 16-го по 24-й цикл солнечной активности линиями. Поскольку Ар-индекс отражает динамику возмущенности магнитосферы в цикле солнечной активности, то по данным, представленным на рис. 6, можно судить об изменении энергетики магнитосферы.

Таким образом, выделенные нами два типа режимов в динамике магнитосферы различаются не только по показателям перемежаемости, но и по энергетическим характеристикам.

ОБСУЖДЕНИЕ

Магнитосфера Земли характеризуется непрерывным распределенным притоком энергии СВ и последующей ее диссипацией. В таких системах формируется распределенная активная среда, в которой возникают стационарные или зависящие от времени пространственные структуры. Как известно [Horsthemke, Lefever, 1984], даже слабый внешний шум, воздей- ствующий на подобные нелинейные системы, может изменять их состояние. Если на вход простой нелинейной системы воздействовать внешним шумом, то на выходе наблюдается сигнал, распределение амплитуд которого имеет тяжелый хвост. По-види-мому, магнитосфера принадлежит к классу таких систем. В работе [Zotov et al., 2008] показано, что экспериментальная функция распределения суточных значений АР-индекса хорошо аппроксимируется произведением степенной и экспоненциальной функций. Это распределение с тяжелым хвостом, а следовательно, статистика магнитосферной динамики может быть описана с помощью приведенной выше модели.

Результаты анализа кумулятивных функций распределений амплитуд А p -индекса и его спектров мощности показали, что, независимо от деления режимов активности магнитосферы на периодические и хаотические, поведению А р -индекса присуща перемежаемость. Однако показатели перемежаемости для двух режимов значительно различаются. Иными словами, стохастическое поведение магнитосферы описывается различными показателями в периодическом и хаотическом режиме. Поскольку показатель степенной функции отражает состояние среды [Малинецкий, Потапов, 2000] , можно на качественном уровне сделать некоторые оценки уровня турбулентности магнитосферы. Так, например, по величине показателя перемежаемости α , характеризующего наклон кумулятивных функций распределений амплитуд А _р-индекса (рис. 3), можно увидеть, что в периодическом режиме уровень хаотичности (турбулентности) А р -индекса существенно выше, чем в хаотическом. В связи с этим при периодическом режиме магнитосфера находится в более турбулизованном состоянии, чем при хаотическом. При этом из сравнения спектральных плотностей А р -индекса и показателей γ , характеризующих наклон спектра мощности (рис. 4), следует, что интенсивность широкополосного шума для периодического режима ниже, чем для хаотического.

Подобное стохастическое поведение магнитосферы может быть обусловлено как внешними факторами (реакция магнитосферы на вариации параметров СВ и ММП), так и внутренней динамикой, связанной с накоплением и высвобождением энергии во время магнитных бурь и суббурь [Johnson, Wing, 2005]. Влияние внешних источников на динамику Ар-индекса в цикле солнечной активности подробно рассмотрено, например, в работе [Holappa et al., 2014]. Согласно результатам этой работы, в фазу подъема и максимума солнечной активности геомагнитная активность в основном обусловливается корональными выбросами массы, тогда как на фазе спада солнечного цикла геомагнитная активность определяется преимущественно высокоскоростными потоками СВ из корональных дыр. Хаотический режим, для которого характерно доминирование широкополосного интенсивного шума, скорее, связан с корональными выбросами массы. Периодический режим, характеризуемый значительным доминированием 27-дневной периодичности по сравнению с шумом, обусловлен рекуррентными высокоскоростными потоками, связанными с 27-дневным периодом вращения Солнца.

Полученная зависимость А р -индекса от β-пара-метра СВ подтверждает влияние внешних факторов на динамику магнитосферы. Как следует из рис. 5, в случае хаотического режима А р -индекс достигает максимальных значений, когда плазменное давление не превышает магнитного давления (β<1). Для периодического режима типична обратная ситуация, а именно максимум А _р-индекса наблюдается при преобладании плазменного давления над магнитным давлением (β>1).

Следует заметить, что в статистическом распределении величины параметра β СВ отмечается максимум частоты наблюдения при β<1 [Веселовский и др., 2010] . По оценкам [Xu, Borovsky, 2015] , величина β в зависимости от типа источника плазмы СВ варьирует от 0.13 до 0.98 при среднем значении 0.71. Согласно [Чернышев и др., 2014] от величины β существенно зависит уровень турбулентности космической плазмы. Полученные статистические характеристики А р -индекса и факт наблюдения периодического и хаотического режимов в динамике магнитосферы при различных диапазонах изменения β указывают на то, что степень турбулентности магнитосферы при β>1 выше, чем при β<1. Это заключение, на первый взгляд, кажется весьма неожиданным. Другими словами, в случае хаотического режима (β<1) внешний шум (турбулентность СВ) подавляет переход магнитосферы в турбулентный режим. Однако в работе [Horsthemke, Lefever, 1984] , в которой исследовались особенности влияния внешнего шума на переход нелинейных систем к турбулентности, показано, что внешний шум стабилизирует хаос. По-видимому, в магнитосфере наблюдается аналогичная ситуация, т. е. для хаотического режима внешнее воздействие турбулентного СВ приводит к стабилизации хаоса.

Не исключено также, что перемежающееся поведение А р -индекса определяется собственной динамикой магнитосферы и может быть описано небольшим числом детерминированных уравнений. Простой критерий, который позволяет различать системы, демонстрирующие детерминированный хаос, и системы, подверженные внешнему шуму, заключается в том, что спектры мощности временных рядов, описывающие системы с детерминированным хаосом, должны падать быстрее любой степени обратной частоты, например экспоненциально [Sigeti, Horsthemke, 1987] . И хотя общего теоретического решения проблемы поведения спектров мощности детерминированных или стохастических систем не найдено до сих пор, численные эксперименты подтверждают этот вывод [Sigeti, 1995; Ohtomo et al., 1995; Valsakumar et al., 1997] . Обнаруженное нами экспоненциальное поведение спектров мощности А р -индекса (рис. 4) свидетельствует о том, что магнитосфера Земли обладает собственной динамикой, которую можно рассматривать в рамках моделей детерминированного хаоса. Таким образом, экспоненциальный характер спектров мощности А р -индекса

(рис. 4) и полученная зависимость А р -индекса от параметра β (рис. 5) показывают, что в целом возмущен-ность магнитосферы в цикле солнечной активности зависит от ее собственной динамики и внешнего фактора, такого, например, как соотношение плазменного и магнитного давления.

Помимо рассмотренных выше различий статистических показателей А р -индекса для периодических и хаотических режимов необходимо обратить внимание на различия двух режимов активности магнитосферы, которые проявляются в энергии флуктуаций А р -индекса (рис. 6). В некоторых циклах солнечной активности энергия флуктуаций А р -индекса в хаотическом режиме значительно превышает энергию флуктуаций в периодическом режиме. Эта закономерность становится понятной, если обратиться к результатам работы [Ермолаев и др., 2009] . Действительно, максимум частоты наблюдения всех геоэффек-тивных крупномасштабных течений солнечного ветра, определяющих геомагнитную активность, соответствует величине β ~1 [Ермолаев и др., 2009] . Именно при β ~1 А р -индекс достигает максимальных значений в хаотическом режиме (рис. 5). Таким образом, можно предположить, что хаотический режим в динамике магнитосферы связан с поступлением большей энергии СВ в каждом цикле солнечной активности по сравнению с периодическим режимом.

В заключение обратим внимание на следующую закономерность. В работе [Лившиц, Обридко, 2006] приведена циклическая вариация угла 9 наклона оси магнитного диполя Солнца, отсчитываемого от плоскости солнечного экватора (широта). Если сопоставить ее с циклической вариацией параметра β, представленной на рис. 2, г , то нетрудно увидеть, что в~1, когда угол 9 ~0-30 ° . При 9 >30 ° в>>1. Следовательно, хаотический режим в динамике магнитосферы наблюдается при 9 <30 ° , а периодический — при 9 >30 ° . С другой стороны, согласно [Sokolov et al., 2013] на орбите Земли плазменное и магнитное давления сравнимы по величине (β ~1) при углах наклона оси магнитного диполя Солнца, близких к нулю. Таким образом, величина параметра β в цикле солнечной активности зависит от угла наклона оси магнитного диполя Солнца к плоскости эклиптики. Исходя из вышесказанного и полученных нами результатов, можно предположить, что глобальным фактором, определяющим триггерный эффект активности магнитосферы, является циклическая вариация угла наклона оси магнитного диполя Солнца к плоскости эклиптики.

ЗАКЛЮЧЕНИЕ

В данной работе показано, что отношение теплового давления к магнитному давлению солнечного ветра является ключевым параметром, определяющим не только триггерные режимы в динамике магнитосферы в цикле солнечной активности, но и влияющим на статистические свойства Ар-индекса. Кумулятивные функции распределения амплитуд и спектры мощности Ар-индекса как для периодиче- ского, так и для хаотического режима хорошо аппроксимируются степенными и экспоненциальными функциями соответственно. При этом показатели степенных функций и показатели, характеризующие наклон спектра Ар-индекса, существенно различаются по величине для периодического и хаотического режима. Обнаружено, что величина Ар зависит от параметра β и характер этой зависимости нелинейный для обоих режимов в динамике магнитосферы. Максимум Ар-индекса для периодического режима наблюдается при β>1, а хаотического — при β<1. Установлено, что в большинстве циклов солнечной активности энергия флуктуаций Ар-индекса для хаотического режима выше, чем для периодического. Полученные результаты свидетельствуют о перемежаемости и связанной с ней турбулентности, наблюдаемой в активности магнитосферы Земли при резком переходе от периодического режима к хаотическому в цикле солнечной активности. Экспоненциальная зависимость спектральной плотности Ар-индекса указывает на то, что поведение магнитосферы определяется ее внутренней динамикой, которую можно описать небольшим числом детерминированных уравнений. На основании связи Ар-индекса с параметром β и зависимости β от угла θ можно предположить, что изменение угла наклона оси магнитного диполя Солнца к плоскости эклиптики является глобальным фактором, определяющим смену режимов или триггерный эффект в динамике магнитосферы в цикле солнечной активности.

Работа выполнена по теме «Влияние космических факторов на развитие экстремальных процессов в магнитосфере Земли», госзадание № 01442014-00116.