Влияние переменного электрического поля на систему DPPC-мембраны в водном растворе NaCl
Автор: Злочевский И.И., Завьялов Д.В.
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Физика и астрономия
Статья в выпуске: 3 т.26, 2023 года.
Бесплатный доступ
В работе представлено исследование влияния переменного электрического поля на DPPC-мембрану, погруженную в водный раствор с ионами NaCl. В исследовании была использована крупно-зернистая модель DPPC-мембраны. Моделирование молекулярной динамики было проведено с использованием пакета для молекулярной динамики GROMACS. Анализ результатов основывался на регистрации изменения распределения заряда таких групп частиц, как: PO4, NC3, Na и Cl. С целью выявления у данной системы свойств, характерных для конденсатора, был проведен расчет зависимости значения общего заряда ионов Na и Cl к разности потенциалов на коробке исследуемой системы. Полученные результаты могут быть использованы как дополнение к практическим исследованиям, а также применены для теоритеческого исследования электрофизических свойств липидных мембран.
Dppc-мембрана, переменное электрическое поле, молекулярная динамика, крупнозернистая модель, конденсатор
Короткий адрес: https://sciup.org/149144544
IDR: 149144544 | УДК: 537.29 | DOI: 10.15688/mpcm.jvolsu.2023.3.8
Текст научной статьи Влияние переменного электрического поля на систему DPPC-мембраны в водном растворе NaCl
DOI:
Hydrodynamic instabilities due to the inhomogeneity of the gas flow can be responsible for the most diverse manifestations at different scales in galaxies. Nonlinear stages of unstable waves in gas are considered to explain the fine structure of astrophysical jets in protostellar systems [21; 32] and extragalactic jets associated with AGN [37], turbulence in accretion disks (AD), including AD in close binary systems [11], turbulent viscosity in gas disks of galaxies, protoplanetary systems, and circumplanetary rings [13-15].
The shear nature of the flow can be the cause of several instabilities in the gas. The instability of the acoustic resonance type instability (ARTI) is accompanied by an exponential increase in the amplitude of the waves with a specific energy exchange with the main flow [10-12; 15; 21; 22; 26]. Amplitude growth is caused by the superreflection effect when a wave falls on a shock or a layer with a strong gradient of the tangential velocity component [11; 12]. Such a layer of gas can lead to the reflection of waves with an increase in amplitude compared to the incident wave. The second mechanism of this instability is related to the resonant energy exchange between the sound wave and the main flow in the critical layer [26]. The appearance of resonance requires that the tangential velocity discontinuity be smoothed out and the velocity shear zone be of finite width [2; 33]. This thin critical layer is the source of instability of a resonant nature. The propagation of small-scale unstable sound waves inside a thin disk can lead to gas turbulence, providing a high level of turbulent viscosity [14; 15;27].
Of particular interest is the global instability in the gas disk, which is due to the radial inhomogeneity of the gas disk rotation curve Vg(r) [7; 8; 26; 36]. It is important to note that there are a number of experimental studies confirming the theoretical conclusions about the conditions for the development of such types of hydrodynamic instabilities. Special equipment creates rotating shallow water with a given rotation profile, making it possible to reproduce strong centrifugal instability in the presence of a local rotation zone with rdVg/(Vgdr) < n^1^ [6; 28]. Such natural experiments demonstrate the formation of trailing spiral patterns with different numbers of arms [8-10]. The richness of morphological features in the spiral structures of galaxies can also be provided by various kinds of instabilities in the gas [13; 17;25;26;31].
The hydrodynamic instabilities listed above allow the formation of turbulent motions, which is an important factor in the development of gravitational instability at different scales, from planetesimals, planets, and star formation to the generation of spiral patterns and morphological large-scale features in galaxies [3; 19]. Moreover, processes in the gaseous disk should be considered together with instabilities in the stellar subsystem [16; 24; 29; 31].
The central region of many spiral galaxies contains one of two types of reasonably dense stellar structures, such as stellar bars (triaxial ellipsoids of rotation) or dense circumnuclear disks. The generation of a spiral structure in SB galaxies seems to be natural due to the strongly nonaxisymmetric gravitational potential. Our efforts are aimed at studying the role of dense circumnuclear stellar disks on the dynamics of gaseous subsystems in the central regions of spiral galaxies. The construction of equilibrium models of galaxies with a complex composite disk is necessary for the numerical simulation of instability at the nonlinear stage as an initial state.
1. Rotation in the gravitational field of homogeneous disk
In this paper, we will consider simple models of matter distribution in the disk component, which allows us to study rather arbitrary radial profiles of the circular rotation velocity Vc with controlled features. Such model dependences of the rotation profile make it possible to subsequently analyze the stability of linear waves, revealing the conditions for the onset of instability. This approach is a necessary and reliable basis for nonlinear hydrodynamic modeling.
The balance of forces in a thin, axisymmetric gaseous galactic disk is [26]
аг/»> ас/ r 0^9) Эт dr ’ where V9 is the velocity of gas rotation, p^ is the pressure, a^ is the surface density of gas, U is the total gravitational potential from all components. The second term in (1) is small in galactic disks at typical parameters. Therefore, if we neglect it, then the rotation velocity Vg is equal to the circular velocity, that is
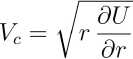
Therefore, the equality Vg = Vc is satisfied below in all calculations.
The gravitational potential is constant (U = const) inside a thin homogeneous sphere with radius R and coincides with the model of a point body of the same mass outside this radius. A thin, homogeneous ring creates a gravitational potential, that is fundamentally different from the potential of the sphere. The potential in the region r < R (R is the radius of the ring) is
U(r) = -4G\vK
where ц is the linear density of the ring ([g/cm]), к = r/R, K(k) is the complete elliptic integral of the first kind [20]. The potential of the outer region r > R is equal to
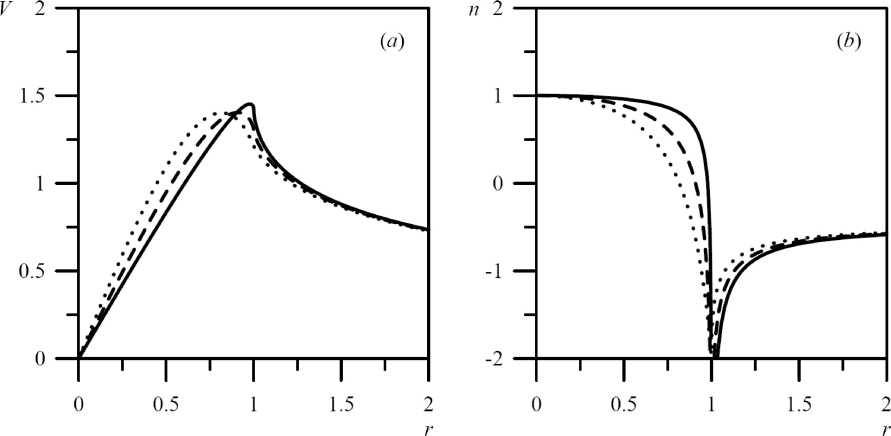
U^ = -4GpkK where к = R/r. The summation of the ring potentials makes it possible to calculate the potential of a disk with an arbitrary radial density profile and the corresponding circular velocity in a thin disk model. The degree of differential rotation is conveniently characterized by the local parameter, that is n(r) dln(I4) d In (r) The dimensionless parameter n determines the inhomogeneity of rotation. The case n = = —1/2 corresponds to the Keplerian rotation curve. We use a system of units in which the characteristic radius is R = 1, the mass of the component is M = 1, and G = 1 is the gravitational constant. This allows you to easily compare the results of calculations for different disk models. Moreover, such non-dimensionalization is often used in numerical simulations [18]. Fig. 1. a) The rotation curve of Vrot(r) in a thin homogeneous disk (solid line). For comparison, the dashed curve shows the rotation curve K(H in the field of a homogeneous ball of the same mass as the disk, b) Radial dependence of n(r) in homogeneous disk Consider first the model of a homogeneous disk of finite radius: if r < R if r > R where о is the surface density. The dimensionless surface density of such a disk is o"0 = 1 /тт. Figure 1 shows the corresponding circular velocity. A homogeneous disk is an idealized mathematical model, which leads to the appearance of singularities in the rotation curve. More realistic models of inhomogeneous disks do not contain such features.
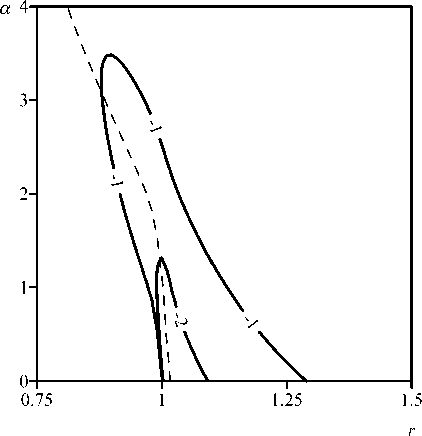
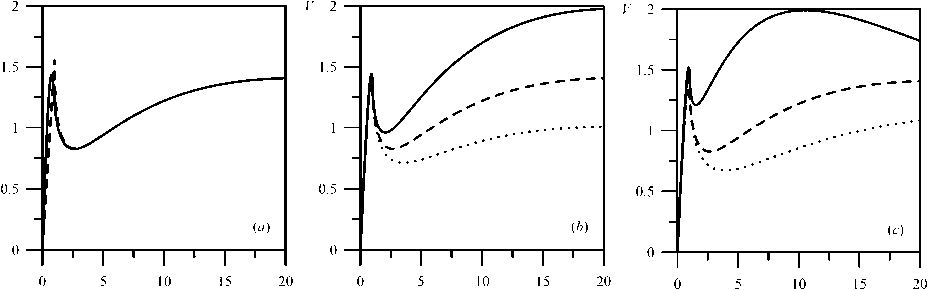
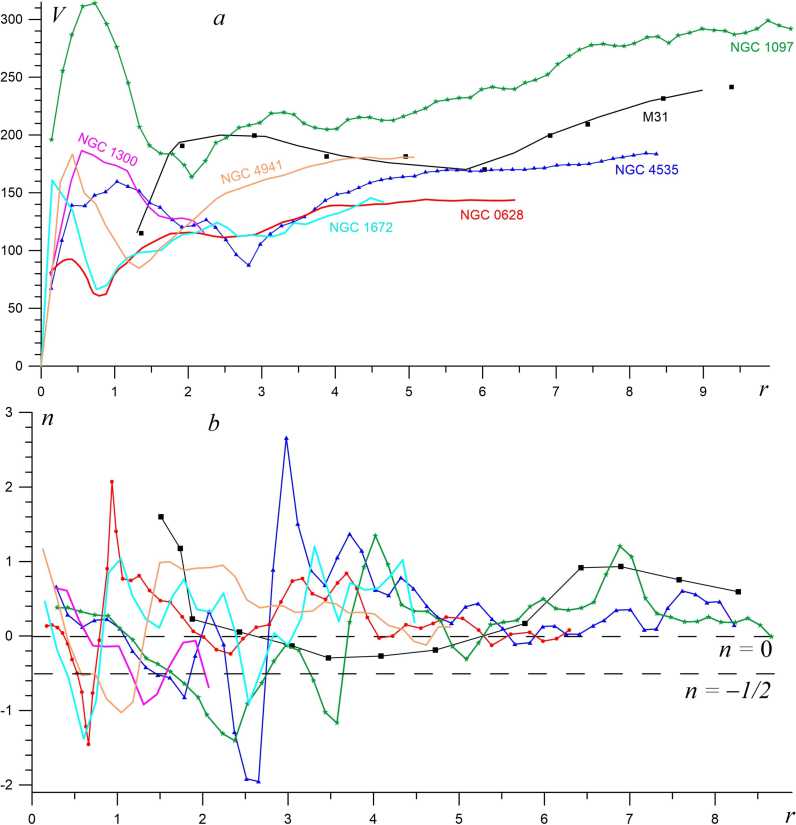
2. Rotation in the gravitational field of inhomogeneous disks The surface density in the power disk model is c(r) = (T0 where oc > 0, oq = (1 + а)/л. We use the following terminology. Disks with а < 1 are hard disks because dcr(r) hm —-— = — oo . (8) dr Disks with ex > 1 are soft, and the asymptotic solution is , dcr(r) hm —-— = 0 . гн-я dr Disk with cc = 1 is said to be normal when executing: . do(r)4 hm —-— =. r^R dr71 Note also that the disk (7) at a = 0 turns into the homogeneous disk considered above. Fig. 2. a) Circular velocity K(H in an inhomogeneous disk (7) in models of different hardness, b) Radial dependences of the index n(r) in an inhomogeneous disk (7) of different hardness: a = 1.50 (dotted line), a = 1.00 (dashed Une), a = 0.67 (solid Une) The method of summing the potentials of rings of different densities provides the construction of the gravitational potential of a disk with an arbitrary density profile. The potential of the inner region of the disk (r< 1) is equal to Computing for the outer region (r > 1) gives U(r)=4r / ko(kr)K(k) dk. Jo ' Figure 2 shows examples of V^r) and n(r) calculations for model (7) in hard (a = = 0.67), normal (ex = 1.0), and soft (ex = 1.5) disc variants. The curves n(r) for these disks are shown in figure 2, b. These results allow us to draw the following conclusions about the disk kinematics with an increase in the parameter ex: 1) The maximum of the rotation curve Vc(r) slightly decreases and shifts noticeably towards the center of the disk. 2) The inflection point near the radius r ~ 1 becomes more pronounced. 3) The width of the region with strong inhomogeneity of rotation decreases (see figure 2,b). Fig. 3. Region boundaries of —2 < n(r) < —1 on the plane (r, a) in models (7). The dashed line shows the position of the inflection point of the curve Vc^ The last two factors are directly related to the possibility of developing shear instabilities in a light gaseous subsystem rotating in the field of a massive stellar disk (7). The development of the Kelvin—Helmholtz instability requires the presence of the region with n(r) < —1 in a weakly compressible medium. More important is the centrifugal instability, for which the occurrence criteria are described in the monograph by Morozov and Khoperskov [26]). We have calculated the boundaries of the zones where the index n(r) takes the values n(r) = —1 and n(r) = —2, since the rotation curves of real galaxies with n(r) < —2 apparently do not occur. Figure 3 shows the isolines n = —1 and n = — 2 on the plane of parameters (r, a). We conclude that Kelvin—Helmholtz instabilities and centrifugal instability can manifest themselves in gaseous subsystems rotating in gravitational fields, even in fairly soft models of stellar circumnuclear disks. Real stellar disks of spiral galaxies in the first approximation can be represented by a composite model, which consists of two disks. The main one is a massive disk with a characteristic inhomogeneity scale along the radial coordinate R2 ^> Ri and mass M2 ^> Mi. The second is a circumnuclear disk of radius Ri and mass Mi, according to model (7). The surface density of the main disk is described by the exponential law: / Г \ o-2(r) = 0-02 exp -— . (13) \ -^2/ The mass of such a disk is ЛА = 2ла02А|. In the system of units adopted by us (Ri = 1, Mi = 1), the following conditions are satisfied: R2 = Pr ^ 1, M2 = рм 3> 1- The ratio of surface densities at the center of compound disk (7), (13) is £02 _ 1 Pm, Ooi 1 + « 2pR' Fig. 4. a) Dimensionless circular rotation velocity for a composite disk with main disk parameters R2 = 10 and M2 = 50 for two models of circumnuclear disks with a = 0.5 (dashed /me)and a = 2.0 (solid line). b) Circular velocity with a normal circumnuclear disk (a = 1) and different main disk masses at R2 = 107?i: M2 = 100 (solid line), M2 = 50 (dashed line), M2 = 25 (dotted line). c) Dependences of the circular velocity of rotation for the composite stellar disk with normal circumnuclear disk (a = 1) and different spatial scales of the main disk at M2 = 50Мг: R2 — 5 (solid line), R2 = 10 (dashed line), R2 = 15 (dotted line) Observational data for spiral galaxies show that the characteristic radial scale of the main stellar disk Rz is several times greater than the radius of the circumnuclear disk Ri, and the mass M2 is approximately two orders of magnitude greater than the mass of the circumnuclear disk Mi. Let us consider the influence of the parameters ex, R2/Ri = Pr^> 1 and M2/Mi = рм > 1 on the total rotation curve in the gravitational field of composite disk (7), (13). The main disk model with parameters R2 = 10 and M2 = 50 is the base one in our calculations. Figure 4 shows the circular velocities in composite disk models. As you can see, there is a two-humped rotation curve due to the presence of a circumnuclear stellar disk. The influence of the parameter oc is not critical and changes the shape of the rotation curve only inside the circumnuclear disk and not far beyond it (see figure 2). Figure 4, b shows the effect of the mass ratio of the main and circumnuclear disks, Рм = М2/Mi on the composite disk rotation curve. An increase in the mass of the main disk leads to a corresponding increase in the outer hump on the rotation curve and has virtually no effect on the size and shape of the inner hump, which is due to the circumnuclear disk. The ratio effect of the characteristic spatial scales of the circumnuclear and main disks on the compound disk rotation curve is shown in figure 4, c. The decrease in the characteristic spatial scale of the main disk leads to two features. 1) The depth of the dip between the humps of the rotation curve decreases. 2) The maximum velocity at the radius of the outer hump increases. The equilibrium gas models are determined by the radial dependences of the surface density of the gas (cr^(r)) and stars (^(r)), the rotation velocity Vg^r), the sound speed cs(r) (or pressure, see (1)). The three-dimensional approach requires considering the volume density p(r, г) instead of the surface density a(r). The dynamics of linear perturbations are determined by the dispersion dependences between the frequency and spatial scales of the waves. The presence of positive increments in the eigenvalue frequency co indicates an exponential growth of unstable perturbations, u/Im) > 0. Some estimates of increments in simple limiting models due to sharp changes in the rotation velocity will be written below. The Kelvin—Helmholtz instability is a classic example of hydrodynamic instability. The presence of a velocity jump at radius R in the subsonic limit gives the expression for the imaginary part of the frequency, that is Ш(М = i^- ((m2 — 1)(1 — y)2)^2 where Qi is the angular velocity of the inner part of the disk (r < RR q = Q2/Qi, H2 is the angular velocity of the outer part of the disk (r > R), m is the azimuthal number of spiral arms. The flow is unstable for any sign of 1 — q, both for Qi > Q2, and otherwise. Centrifugal instability requires a faster rotation of the central zone of the disk (Q2 < < Qi), which gives the increment in the supersonic limit [26]: ш(1т) = ^ ^ ^ (1 - Q2) , where M* = R5.Ljc4 is the characteristic Mach number. Instability is possible only at q< 1, which agrees with the rotation curves in figures 2 and 4. The instability of the acoustic resonance type (IART) is also called the overreflection effect. The general term “Kelvin—Helmholtz instability” (KHI) is used in the English literature to refer to all instabilities associated with a sharp drop in velocity, including the velocity gap between plasma and magnetic field [13]. The use of the term KHI for IART (see, e.g., [40]) in the English literature is incorrect, since the physical mechanisms of these instabilities are different. One solution for the imaginary part of the IART frequency is the following asymptotics: yjdm) = -|- Vm? — 4 at M* » m 3> 1. The formulas (15)-(17) are obtained for the speed jump when the width of the transition layer Lv from Qi to H2 is infinitesimal (Lv = 0). The value of Lv in real systems is finite, which requires additional analysis. A distinctive feature of the above instabilities is their strong dependence on Lv, so that there is always some critical width L(cmt) stabilizing the instability. Fig. 5. a) Examples of galaxy rotation curves ([r] = kpc, [V] = km/sec). b) Radial profiles of parameter n computed for rotation curves on panel a. The line colors on the panels a and b correspond to each other
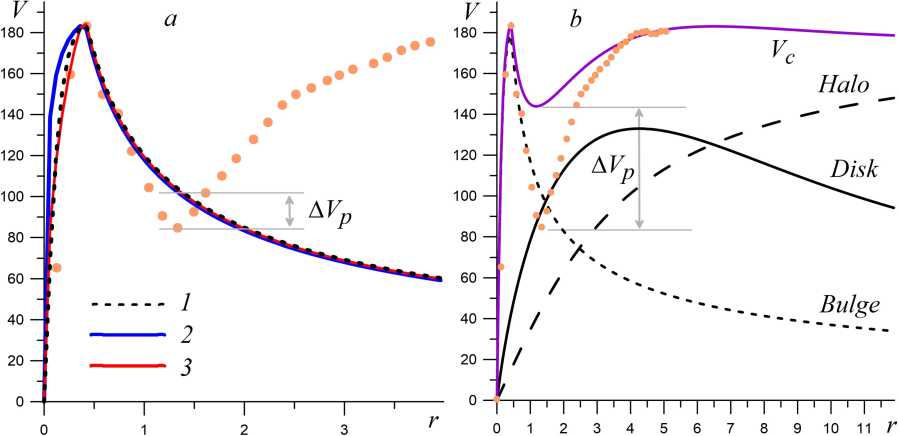
4. Estimates of the inhomogeneity index of the observed rotation curves Figure 5, a shows the radial dependences of the rotation curves of some galaxies in [23;39], which have zones of a sharp decrease in rotation. The result of calculating the parameter n(r) for these objects is shown in figure 5, b. Of main interest are the regions n < 0 and especially n< —1/2 in the central parts of the disks. Four galaxies have strong rotation velocity gradients with n< — 1. Rotation curves with similar features are also observed in the galaxies NGC 157, NGC 615, NGC 253, NGC 2273, NGC 2590, NGC 2599, NGC 2713, NGC 2841, NGC 3031, NGC 3034, NGC 3079, NGC 3531, NGC 3898, NGC 4192, NGC 4303, NGC 4527, NGC 4536, NGC 4548, NGC 4945, NGC 5033, NGC 5236, NGC 6946, UGC 508, UGC 3546, UGC 6787, UGC 08179, UGC 8699 [ 1; 4; 5; 30; 34; 35; 38]. We do not consider the Milky Way here, since the rapid decrease in the rotation velocity in the region of 1-2 kpc is caused by dynamical causes in the region of the central stellar bar [18] and does not characterize the circular velocity. This problem of strong non-axisymmetry of gas motion in the zone controlled by a powerful stellar bar may concern the galaxies NGC 4535, NGC 1097, NGC 1672, NGC 1300, since the azimuthal component of the gas velocity along the major and minor axes of the bar is very different. The galaxies NGC 628 and NGC 4941 do not have a pronounced bar, and their rotation curves reflect the radial mass distribution to a greater extent, allowing one to assume Vg = Vc. Fig. 6. a) Modeling of the central part of the rotation curve of NGC 4941 with different bulge models: King model (line /), de Vaucouleur model (line 2), Sersic model (line 3). b) Complete decomposition of the rotation curve in the three-component model. The circles show the observed rotation law (see figure 5, a) Figure 6 shows the result of the decomposition of the central part of the rotation curve for NGC 4941. No traditional bulge models reproduce the observed decrease in the rotation velocity in the zone near 0.5-1.5 kpc in figure 6, a, where only the bulge contribution is considered. Moreover, we use the bulge model with a sharp density cutoff near the velocity maximum, which is in poor agreement with the photometric data. The formal discrepancy between the observed and model velocity Vc at the local minimum is AV/ = 17 km/sec. Attempts to construct a realistic decomposition in the model with a disk and a halo in figure 6, b immediately increase the discrepancy to AV/ ~ (145 — 85) km/sec = 60 km/sec. Thus, the rotation curve of this galaxy cannot be explained using the standard models of the bulge, thick exponential disk, and dark halo. This possibly indicates the influence of the circumnuclear disk. The decomposition of NGC 628 gives a similar result. Our calculations have shown that a circumnuclear stellar disk with a mass two orders of magnitude smaller than the mass of the main stellar disk of the S-galaxy is capable of creating a pronounced two-peaked gas rotation curve. Examples of such rotation curves for a number of galaxies are shown in figure 5, a. The gradient of the rotation curve in the vicinity of the radius of the circumnuclear stellar disk can be so large that it allows both the Kelvin—Helmholtz instability and the centrifugal instability to develop in the gaseous disk. The uniqueness of these instabilities is due to the fact that their properties have been confirmed in analog experiments based on the theory of shallow water [6-9]. Thus, we believe that the role of circumnuclear stellar disks in galaxies is to create double-humped rotation curves of gas components with a sharp decrease in the gas rotation velocity, allowing hydrodynamic instabilities capable of generating a spiral pattern in the galaxy. The reverse effect of perturbations from the nonlinear hydrodynamic instability on the circumnuclear stellar disk can deform it, forming oval structures like weak bars. The models constructed in this paper are designed to study spiral patterns due to hydrodynamic instabilities in galactic disks as equilibrium initial states in numerical models. Such computational experiments impose special requirements on numerical models since they are required to describe the creation of unstable modes in a very narrow spatial region, the dimensions of which are several orders of magnitude smaller than the entire computational domain. One of the advantages of centrifugal instability as a generator of the spiral structure is the natural explanation of the number of arms in the disk [7]. The purpose of such computational experiments is to test the hypothesis of a hydrodynamic mechanism for the generation of spiral patterns in gas-rich galaxies. Spiral patterns due to hydrodynamic instability should differ in their properties from the mechanisms of gravitational instability or tidal influence. Including “hydrodynamic type” spiral models in a combined machine learning dataset can reveal the role of one mechanism or another in real systems. NOTE 1 This work is supported by the Russian Science Foundation (grant no. 23-71-00016, https:/ / rscf.ru/proj ect/23-71 -000 16/).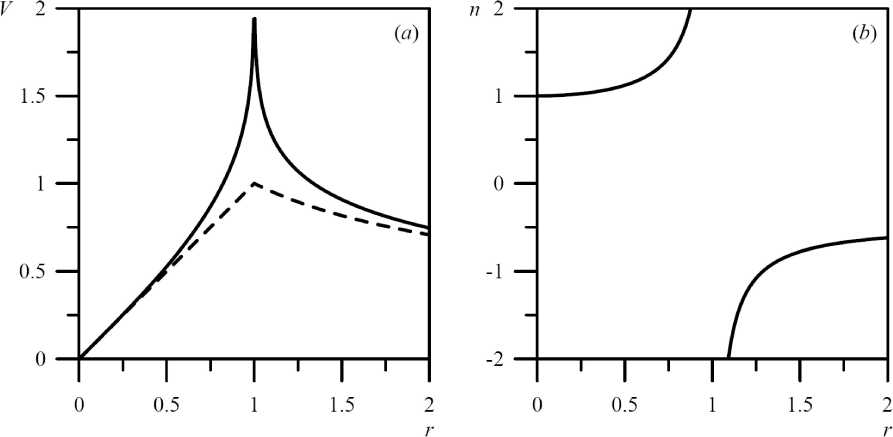
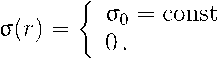
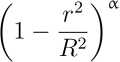
Список литературы Влияние переменного электрического поля на систему DPPC-мембраны в водном растворе NaCl
- Вычислительный кластер ВолгГТУ. — Электрон. текстовые дан. — Режим доступа: https://cluster.vstu.ru/. — Загл. с экрана.
- A Molecular Dynamic Study of Cholesterol Rich Lipid Membranes: Comparison of Electroporation Protocols / M. Casciola, D. Bonhenry, M. Liberti, F. Apollonio, M. Tarek // Bioelectrochemistry. — 2014. — Vol. 100. — P. 11-17. — DOI: https://doi.org/10.1016/j-.bioelechem.2014.03.009
- Delemotte, L. Molecular Dynamics Simulations of Lipid Membrane Electroporation / L. Delemotte, M. Tarek // The Journal of Membrane Biology. — 2012. — Vol. 245. — P. 531-543. — DOI: https://doi.org/10.1007/s00232-012-9434-6
- El-Beyrouthy, J. Characterizing the Structure and Interactions of Model Lipid Membranes Using Electrophysiology / J. El-Beyrouthy, E. Freeman // Membranes. — 2021. — Vol. 11, № 5. — P. 319. — DOI: https://doi.org/10.3390/membranes11050319
- Krems, M. Ionic Memcapacitive Effects in Nanopores / M. Krems, Y. V. Pershin, M. Di Ventra // Nano letters. — 2010. — Vol. 10, № 7. — P. 2674-2678. — DOI: https://doi.org/10.1021/nl1014734
- Lin, X. Transmembrane Potential of Physiologically Relevant Model Membranes: Effects of Membrane Asymmetry / X. Lin, A. A. Gorfe // The Journal of Chemical Physics. — 2020. — Vol. 153, № 10. — P. 105103. — DOI: https://doi.org/10.1063/5.0018303
- Membrane Potential and Dynamics in a Ternary Lipid Mixture: Insights from Molecular Dynamics Simulations / X. Lin, V. Nair, Y. Zhou, A. A. Gorfe // Physical Chemistry Chemical Physics. — 2018. — Vol. 20, № 23. — P. 63-91. — DOI: https://doi.org/10.1039/C8CP01629A
- Membrane Electroporation and Electropermeabilization: Mechanisms and Models / T. Kotnik, L. Rems, M. Tarek, D. Miklavcic // Annual Review of Biophysics. — 2019. — Vol. 48. — P. 63-91. — DOI: https://doi.org/10.1146/annurev-biophys-052118-115451
- Pluhackova, K. Molecular Dynamics Simulations of Membrane Proteins / K. Pluhackova, T. A. Wassenaar, R. A. Bockmann // Membrane Biogenesis. Methods in Molecular Biology. — 2013. — Vol. 1033. — P. 85-101. — DOI: https://doi.org/10.1007/978-1-62703-487-6_6
- Rakesh, G. Electroporation of Skin Stratum Corneum Lipid Bilayer and Molecular Mechanism of Drug Transport: A Molecular Dynamics Study / G. Rakesh, R. Beena // Langmuir. — 2018. — Vol. 34 (20). — P. 5860-5870. — DOI: https://doi.org/10.1021/acs.langmuir.8b00423
- Yadollahpour, A. Electroporation as a New Cancer Treatment Technique: A Review on the Mechanisms of Action / A. Yadollahpour, Z. Rezaee // Biomedical and Pharmacology Journal. — 2015. — Vol. 7, № 1. — P. 53-65. — DOI: https://dx.doi.org/10.13005/bpj/452


