Влияние переменного коэффициента термодиффузии на конвекцию бинарной смеси в прямоугольных полостях

Исследования тепломассопереноса в многокомпонентных смесях с учетом диффузии и термодиффузии имеют обширную область приложений. Примерами могут служить добыча углеводородов [1], фильтрация загрязняющих примесей [2 – 4], их распространение [5 – 8], восстановление геотермальной энергии [9]. Аналогичный подход применим и к моделированию сложных биологических жидкостей, коллоидных суспензий, металлов [10 – 14].

Для учета эффектов диффузии и термодиффузии требуется знать значения коэффициентов переноса. Существует много работ, посвященных определению коэффициентов переноса в конкретных многокомпонентных смесях при различных фиксированных внешних условиях (значениях температуры, давления) и разных соотношениях массовых долей компонентов смеси [15 – 19]. В ряде работ

коэффициенты диффузии и термодиффузии (Соре) найдены как функции температуры и концентрации компонентов смеси [15, 20 – 27]. Анализ литературы показывает, что бинарные органические жидкие смеси по характеру зависимости коэффициента Соре от температуры и концентрации можно разделить на три группы. Первая группа демонстрирует сохраняющуюся с ростом температуры немонотонную связь коэффициента Соре с концентрацией, которая не меняется с ростом температуры [25, 26]. Для второй группы свойственно также немонотонное уменьшение модуля коэффициента Соре с увеличением температуры, а значение концентрации, при которой происходит смена знака коэффициента Соре, не зависит от температуры [27]. Смеси третьей группы имеют температурную инвариантную точку, в которой на коэффициент Соре, не равный нулю, температура не влияет [15, 26].

Обычно при моделировании конвективных явлений в смесях предполагается, что отклонения температуры и концентрации от средних (или начальных) значений малы, поэтому температурные и концентрационные изменения коэффициентов переноса не учитываются [28 – 30]. Однако в случае достаточно больших градиентов температуры и концентрации переменность коэффициентов может существенно влиять на поведение смеси. В работе [31] анализируется влияние температурной и концентрационной обусловленности коэффициента Соре на распределение примеси бинарной смеси в отсутствие естественной конвекции.

В настоящей работе исследуются возникновение и нелинейные режимы конвекции водного раствора NaCl в горизонтальной прямоугольной полости при подогреве снизу. Перепад температур между нижней и верхней границами составляет 40 градусов. Моделирование проводится с учетом полиномиальной зависимости коэффициента термодиффузии от температуры [21, 31], особенностью которой является то, что коэффициент термодиффузии при определенном значении температуры меняет знак. В работе выбран для обсуждения такой диапазон температур, что смена знака коэффициента термодиффузии происходит внутри полости. Другие коэффициенты переноса считаются постоянными.

2.    Постановка задачи и метод решения

Рассматривается термоконцентрационная конвекция бинарной смеси в квадратной и вытянутой по горизонтали прямоугольной областях при нагреве снизу (Рис. 1). Плотность смеси р считается линейно зависящей от температуры T и концентрации примеси C :

р = Р о ( 1-р _г ( T - Т о ) -р _с ( С - C o ) ) .

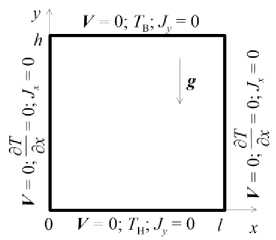
Рис. 1. Геометрия и граничные условия задачи

Здесь: Pr = (-1 Ро)(др/дТ)|с и Рс = (-1ро)(др/дС)|г — коэффициенты теплового и концентрационного расширения соответственно; р0, Со и То — средние значения плотности, концентрации примеси и температуры смеси.

Эффекты бародиффузии и диффузионной теплопроводности в расчет не принимаются. Коэффициенты вязкости v , молекулярной диффузии D и температуропроводности % считаются постоянными, а коэффициент термодиффузии D предполагается зависящим от температуры по полиномиальному закону в соответствии с работами [21, 31].

С учетом сделанных допущений нестационарные уравнения термоконцентрационной конвекции бинарной смеси в приближении Буссинеска имеют вид:

д V +(V-V) V ^Vp + vV2V + [1-р Т (Т - То )-р с (с - Со)] g, дТ + (V -V) Т = %а Т,(3)

дС + (V -V) С = D А С + DT (Т )А Т,(4)

V-V = о.(5)

Здесь: V — вектор скорости; p — давление; g — вектор ускорения силы тяжести; символ д, обозначает производную по времени t ; V — оператор набла; А — двумерный лапласиан.

Границы полости считаются твердыми, непроницаемыми для вещества. Их горизонтальные составляющие поддерживаются при постоянных, но разных температурах, соответствующих подогреву снизу, боковые — теплоизолированы. Граничные условия для концентрации заключаются в равенстве нулю диффузионного потока вещества J (Рис. 1):

x = 0; l :	V = 0,	d T = °, dx	J x =	ar . = -P0 D — + D т ( T )—: оx        оx	= 0,	(6)
y = 0:	V = 0,	T = T 1    1 h,	J y =	a -        t -p 0 D^T + D t ( T )^7 = dy       dy	0,	(7)
y = h:	V = 0,	T = T 1     1 В ,	J y =	naс n ,та t_ -po D ""Г"+ D T ( T ) "Г" =	0.	(8)

Рассмотрены квадратная полость со стороной 0,01 м и прямоугольная полость длиной l = 0,05 м и высотой h = 0,01 м. Температура на нижней границе принималась равной Т_н = 318 К, а на верхней — Т_в = 278 К. Расчеты выполнены для значений ускорения силы тяжести g : g = g ₀, что соответствует земным условиям, а также при g = g ₀ -10 ¹ и g = g ₀ -10 2 , то есть в условиях пониженной гравитации.

Объектом исследования служил водный раствор NaCl с массовой долей растворенного вещества С₀ = 0,0285 при средней температуре Т = 298 К. Тепловые и физические параметры этой смеси представлены в таблице и взяты из работ [31–33].

Таблица. Тепловые и физические параметры водного раствора NaCl

p 0 , кг/м3	V , м2/с	X , м2/с	P t , К-1	в -	D , м2/с
1050,0	1,03 - 10 -6	1,47 - 10-7	1,9 - 10-4	-0,755	1,512 - 10-9

Коэффициент термодиффузии считался зависящим от температуры по следующему закону [21, 31]:

DT (Т)«10-10 (1,463 - 0,00885Т + 0,0000131Т2) м2/(с-К).                       (9)

При температуре Т _о = 298 К он равнялся D_T ~ - 1,58 - 10 ^{- 12}м²/(с - К); при разности температур 40 К, согласно (9), внутри области коэффициент термодиффузии менял знак; при температуре Т * ® 285,4 К изменялся от верхней границы полости до нижней в диапазоне от - 2,66 - 10 ^{- 11} до 2,33 - 10 ^{- 11} м²/(с - К).

В начальный момент времени полагалось, что жидкость неподвижна, концентрация примеси в полости однородна, температура линейно зависит от вертикальной координаты.

Вычисления осуществлялись в программном пакете ANSYS Fluent, реализующем метод конечных объемов. Применялась равномерная по пространственным переменным сетка с квадратными ячейками, шаг сетки составлял 5 - 10 ^{- 5} м, шаг по времени был постоянным и равным 1 с. Выбранные размеры расчетной сетки обеспечивали 5 узлов для разрешения концентрационного пограничного слоя. Для дискретизации уравнений использовался второй порядок аппроксимации по времени и третий — по пространству.

3.    Численные результаты

При учете полиномиального вида D_T ( Т ) (9) в той части полости, где температура выше Т * ® 285,4 К, коэффициент термодиффузии является отрицательным. Это означает, что, благодаря эффекту термодиффузии, тяжелый компонент смеси накапливается в более нагретой зоне полости, а легкий диффундирует в более холодную зону. В случае подогрева снизу в полости формируется устойчивая стратификация смеси по плотности. Наоборот, при подогреве сверху зависимость плотности от температуры приводит к неустойчивой плотностной стратификации. Тогда, как известно из [34], при определенном значении числа Релея механическое равновесие смеси становится неустойчивым, причем конвекция всегда возбуждается монотонным образом.

В верхней части полости, где температура ниже Т * ® 285,4 К и, согласно (9), коэффициент термодиффузии положителен, под действием термодиффузии возникает устойчивая стратификация по плотности, не вызывающая конвективного течения. Однако можно ожидать, что течение из нижней части полости проникнет и в эту область и, как следствие, произойдет разделение смеси, но оно, по сравнению со случаем постоянного коэффициента термодиффузии, будет меньшим.

• 3.1.    Квадратная полость

  • 3.1.1.    Случай действия земной силы тяжести. Рассмотрим воздействие на смесь земной силы тяжести. При этом заданные в настоящей работе условия соответствуют числу Релея Ra = g Р_ГА Th³ /(vx ) ® 1,23 - 10 5 ,

    кг/(мс)

    
    

    — D_T = const

    --DAT)

    0,016 -

    0,012-

    0,008 -

    
    
    

    0,004 -

    
    
    
    
    
    
    
    

    а

    
    
    

    б

    
    

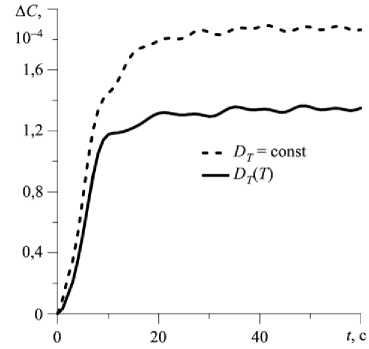
    Рис. 2. Временная эволюция в полости максимального значения функции тока (?) ( а ) и разности концентраций между центрами верхней и нижней границ ( б ) при действии земной силы тяжести

    
    
    

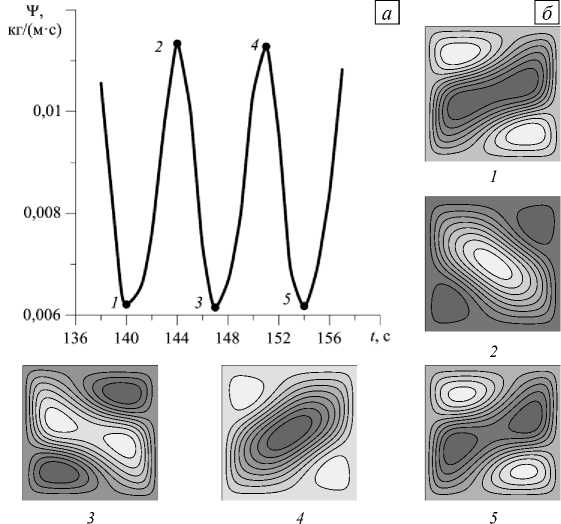
    Рис. 3 . Фрагмент временной эволюции максимального значения функции тока в полости ( а ) и изменение поля функции тока за период колебаний ( б ) под воздействием земной силы тяжести

    
    

что значительно превышает его критическое значение Rac = 2,98 -103, найденное     при     постоянном коэффициенте термодиффузии, равном DT e 1,58-10-12м2/(с-К).

В используемом  для расчетов программном пакете ANSYS Fluent функция тока Y вводится как р u = д^/ду,  р v = -5Y/5x,  где u и v — x - и y -компоненты вектора скорости. На рисунке 2 представлены данные о временной эволюции максимального значения функции тока в полости и разности концентраций примеси между центрами верхней и нижней границ полости, полученные при постоянном значении коэффициента термодиффузии (штриховые линии) и с учетом зависимости (9) (сплошные линии). Как видно, учет D(T) как функции температуры  слабо влияет на образование неустойчивости   и формирование течения. Течение как в случае  постоянного  коэффициента термодиффузии, так и при зависимости его от температуры возникает очень быстро (практически отсутствует бесконвективный период при малых временах), затем имеет место переход к колебательному режиму (Рис. 2а). При учете D(T) происходит лишь некоторое увеличение интенсивности течения. Влияние изменения направления градиента концентрации внутри полости на разделение смеси более существенно, оно приводит к тому, что максимальное разделение смеси в случае переменного коэффициента термодиффузии ниже, чем при его постоянном значении, примерно в 1,4 раза (Рис. 2б).

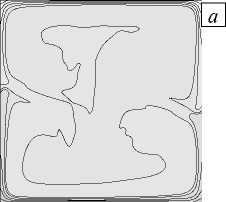
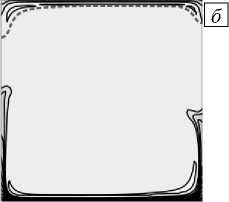
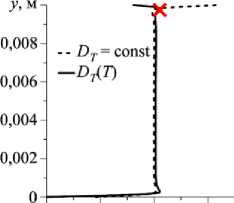
С течением времени устанавливается режим стационарных колебаний с перезамыканием вихрей (Рис. 3), аналогичный наблюдаемому в работе [35] при постоянном коэффициенте термодиффузии. Распределение концентрации в полости однородно в ее центральной части и сильно меняется возле границ (Рис. 4а, б). На рисунке 4б штриховой линией показана изотерма T* = 285,4 К, разграничивающая области, в которых коэффициент термодиффузии имеет разные знаки. Область, где DT (T) положителен, за счет сильного течения прижата к верхней границе полости. Профили концентрации демонстрируют сильные, по сравнению с течением при постоянном D , изменения возле горизонтальных границ полости, также связанные со сменой знака коэффициента термодиффузии в верхней части полости (Рис. 4в). Градиенты концентрации в областях ниже и выше изотермы T* = 285,4 К направлены к ней; максимальное значение

в

0,02 83 0,0284 0,02 85 С

Рис. 4. Распределение концентрации примеси в условиях земной гравитации в момент времени t = 60 с при постоянном (а) и зависящем от температуры (б) коэффициенте термодиффузии (штриховая линия - изотерма T* = 285,4 К, вдоль которой

D_T ( T ) ~ 0 м ² /(с ■ К)); профили концентрации ( в ) вдоль линии x = 0,005 м (символ X соответствует точке, где коэффициент термодиффузии меняет знак)

концентрации примеси вдоль линии x = 0,005 м в случае зависящего от температуры коэффициента термодиффузии достигается именно в точке смены знака D_T ( T ) , в то время как при постоянном D_T максимального значения концентрация смеси достигает на верхней границе полости.

• 3.1.2.    Сила тяжести, в десять раз меньшая земной. При понижении величины силы тяжести конвекция возникает позже: резкий рост интенсивности течения наблюдается при t ® 50с (Рис. 5 а ). В дальнейшем в полости формируется стационарное течение. Поскольку внутри полости происходит смена знака коэффициента термодиффузии при учете, что D ( T ), степень максимального разделения смеси в этом случае уменьшается по сравнению со степенью при постоянном значении D примерно в 1,2 раза (Рис. 5 б ). Это чуть ниже, чем в условиях земной гравитации.

  
  
  
  

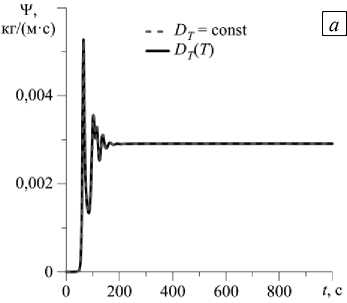
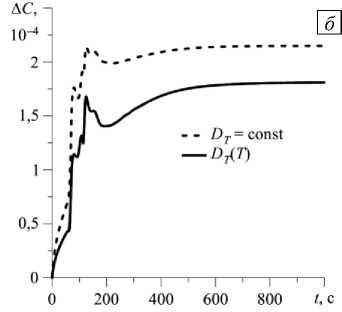
  Рис. 5. Временная эволюция максимального значения функции тока в полости ( а ) и разности концентраций между центрами верхней и нижней границ ( б ) при силе тяжести, в десять раз меньшей земной

  
  

Стационарное течение, возникающее при силе тяжести, в десять раз меньшей земной, имеет 2-вихревую форму как при постоянном значении коэффициента термодиффузии, так и при D ( T ). (Рис. 6а ). Поскольку число Шмидта велико (Sc = у/D = 681), изолинии концентрации «вморожены» в поле течения (то есть оба поля имеют выраженное сходство). Имеются две области, где концентрация практически постоянна, а градиенты наблюдаются вблизи границ полости и на границах вихрей (Рис. 6 б ).

С

в

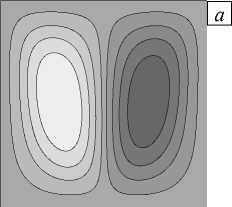
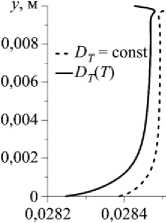
Рис. 6. Изолинии функции тока (а), распределение концентрации (б) при зависящем от температуры коэффициенте термодиффузии; профили концентрации (в) вдоль линии x = 0,005 м при силе тяжести, в десять раз меньшей земной, в момент времени t = 1000 с

В верхней части полости сказывается влияние смены знака коэффициента термодиффузии — максимального значения концентрация достигает в точке, где D T ( T ) ® 0 м²/(с ■ К), к которой направлены градиенты концентрации (Рис. 6 в ). Максимальное значение концентрации в случае постоянного коэффициента термодиффузии имеет место на верхней границе полости.

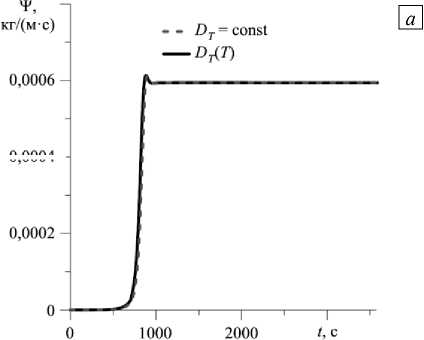
• 3.1.3.    Сила тяжести, в сто раз меньшая земной. При силе тяжести, в сто раз меньшей земной, в квадратной полости реализуется слабое стационарное течение (Рис. 7 а ), которое появляется после достаточно продолжительного бесконвективного периода. Возникновение конвекции сопровождается ростом интенсивности движения, происходящим на отрезке времени от 500 до 850 с. Разделение смеси в стационарном режиме при постоянном значении коэффициента термодиффузии примерно в 1,4 раза выше, чем при учете зависимости D ( T ) (Рис. 6 б ).

  

  0,0004 -

  
  
  

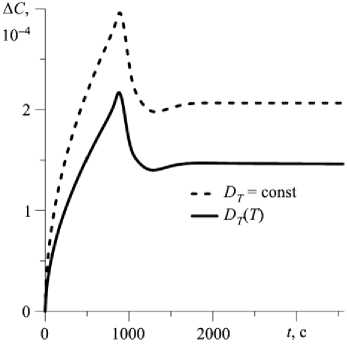
  Рис. 7. Временная эволюция максимального значения функции тока в полости ( а ) и разности концентраций между центрами верхней и нижней границ ( б ) при силе тяжести, в сто раз меньшей земной

  
  

  б

  
  

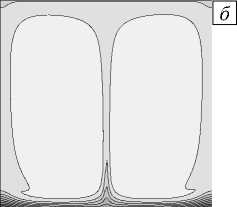
Структура стационарного течения одновихревая (Рис. 8) как при постоянном коэффициенте термодиффузии, так и при D ( T ). При учете температурной зависимости, как и в предыдущем случае, наблюдается «вмороженность» изолиний концентрации в поле течения (Рис. 8 б , в ). Профиль концентрации вдоль линии x = 0,005 м при переменном коэффициенте термодиффузии, показанном на рисунке 8 г сплошной линией, значительно отличается от профиля, полученного при постоянном D (Рис. 8 г , штриховая линия) и качественно похож на профиль в условиях отсутствия конвекции, представленный в работе [31] .

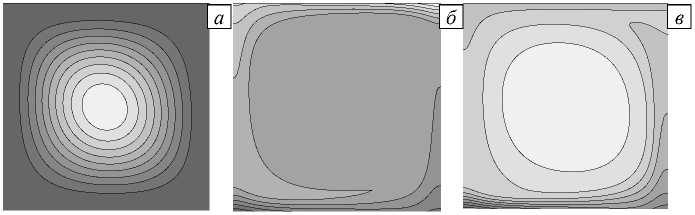
Рис. 8. Изолинии функции тока при зависящем от температуры коэффициенте термодиффузии ( а ), распределение изолиний концентрации при постоянном ( б ) и переменном ( в ) коэффициенте термодиффузии; профили концентрации ( г ) вдоль линии x = 0,005 м при силе тяжести, в сто раз меньшей земной, в момент времени t = 3600 с

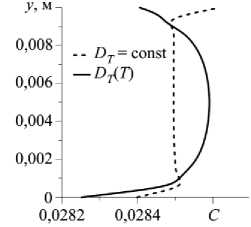
г

• 3.2.    Прямоугольная полость

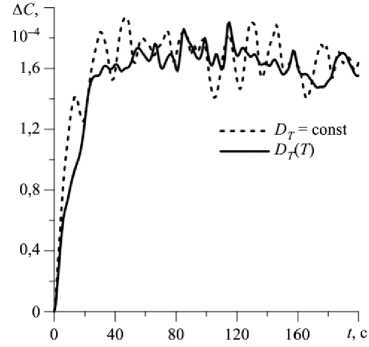
  • 3.2.1.    Земная гравитация. Рассмотрим поведение смеси в прямоугольной полости длиной l = 0,05 м и высотой h = 0,01 м. На рисунке 9 представлены графики временной эволюции максимального значения функции тока в полости и разности концентраций между центрами верхней и нижней границ полости при постоянном ( D_T ~ - 1,58 - 10 ^{- 12}м²/(с ^ К)) и переменном ( D_T(T ) (9)) коэффициенте термодиффузии. Как видно из рисунка, учет зависимости (9) слабо влияет на интенсивность течения, возникающего в полости. В обеих ситуациях наблюдается практически полное отсутствие бесконвективного периода при малых временах, затем образуется сильное течение, имеющее форму нерегулярных колебаний (Рис. 9 а ). Интенсивность течения несколько выше в случае D ( T ), и разделение смеси при этом наступает позже, а его максимальное значение меньше (Рис. 9 б ).

    а

    
    

    кг/(мс)

    
    
    
    

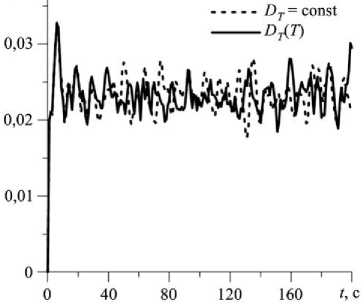
    б

    Рис. 9. Временная эволюция максимального значения функции тока в полости ( а ) и разности концентраций между центрами верхней и нижней границ ( б ) в условиях земной гравитации

    
    

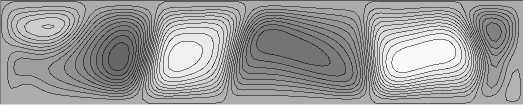
При постоянном и переменном коэффициенте термодиффузии структура течения 4-вихревая, однако в первом случае имеется еще два вихря, более ярко выраженных, чем при зависящем от температуры коэффициенте термодиффузии (Рис. 10). Изолинии концентрации показывают, что в средней части полости ее распределение однородно, а заметные изменения наблюдаются около границ полости (Рис. 11 а , б ). На рисунке 11 в , где представлены вертикальные профили концентрации, видно влияние смены знака коэффициента термодиффузии, а также наличие однородности в распределении концентрации в центральной части полости и ее отсутствие у границ.

а

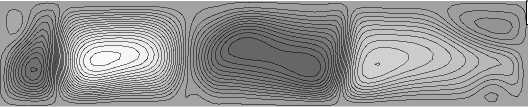
Рис. 10. Изолинии функции тока при постоянном ( а ) и зависящем от температуры ( б ) коэффициенте термодиффузии при действии земной силы тяжести в момент времени t = 200 с

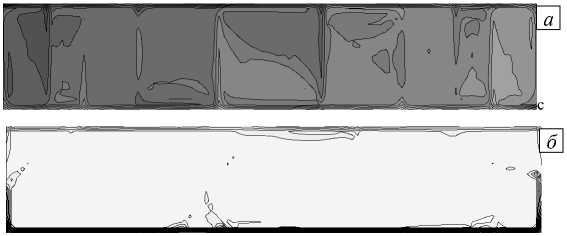
Рис. 11. Распределение концентрации примеси при постоянном ( а ) и зависящем от температуры ( б ) коэффициенте термодиффузии и профили концентрации ( в ) вдоль линии x = 0,005 м при земной силе тяжести в момент времени t = 200 с

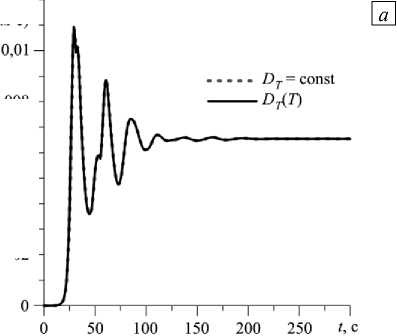
• 3.2.2.    Гравитация, в десять раз меньшая земной. В случае, когда сила тяжести понижена в десять раз относительно земной, появляется бесконвективный период на протяжении t ® 20 с от начала процесса (см. Рис. 12 а ). В течение этого периода происходит близкое к чисто диффузионному разделение смеси (Рис. 12 б ). Затем возникает конвекция, сопровождающаяся резким увеличением интенсивности течения и еще большим ростом степени разделения смеси. Далее течение выходит на стационарный режим. При рассматриваемой величине силы тяжести наибольшие значения разности концентрации примеси в полости в случаях постоянного и переменного коэффициента термодиффузии различаются сильнее, чем при действии земной силы тяжести. Еще заметнее различия по сравнению с квадратной полостью — приблизительно в 1,8 раза (Рис. 12 б ).

  т, -

  кг/(м"С) _

  0.006 -

  0,004 -

  
  
  

  0,008 -

  
  

  0,002 -

  
  
  

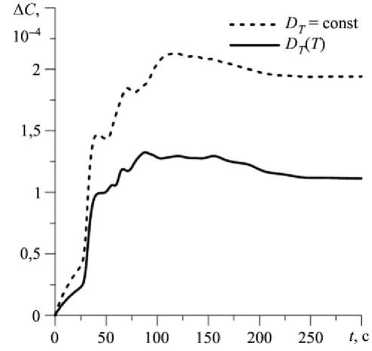
  Рис. 12. Временная эволюция максимального значения функции тока в полости ( а ) и разности концентраций между центрами верхней и нижней границ ( б ) при силе тяжести, в десять раз меньшей земной

  
  

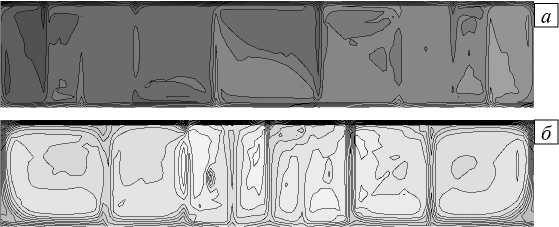
Установившееся в данных условиях стационарное течение имеет 9-вихревую структуру при постоянном D_T и 8-вихревую при переменном D_T ( T ) (Рис. 13). По сравнению со случаем действия земной силы тяжести наблюдается уменьшение пространственного масштаба конвективных вихрей. Число Шмидта велико, из-за этого изолинии концентрации «вморожены» в поле скорости. Появляются девять областей при постоянном коэффициенте термодиффузии и восемь при наличии зависимости D от температуры, соответствующих вихрям на рисунке 13; в этих областях концентрация практически однородна, причем при коэффициенте термодиффузии, меняющем знак внутри полости, «вмороженность» выражена более четко (Рис. 14 а , б ). Профили концентрации показывают, что, как и при действии земной силы тяжести, значение концентрации мало отличается от начального в центральной части полости и значительно — у границ. Однако различие течений смеси с постоянным и переменным коэффициентами термодиффузии при данном уровне гравитации заметнее, потому что в центральной части происходит некоторое отклонение от равновесного значения (Рис. 14 в ). В случае течения при постоянном коэффициенте термодиффузии, в отличие от течения с переменным D_T ( T ) , концентрация примеси наибольшая у верхней границы полости.

Рис. 13. Изолинии функции тока при постоянном ( а ) и зависящем от температуры ( б ) коэффициенте термодиффузии при силе тяжести, в десять раз меньшей земной, в момент времени t = 300 с

б

Рис. 14. Распределение концентрации примеси при постоянном ( а ) и зависящем от температуры ( б ) коэффициенте термодиффузии и профили концентрации вдоль линии x = 0,005 м ( в ) при тяжести, в десять раз меньше земной, в момент

времени t = 300 с

• 3.2.3.    Гравитация, в сто раз меньшая земной. В поле пониженной силы тяжести в прямоугольной полости наблюдается продолжительный бесконвективный период, приблизительно 250 с (Рис. 15а). Дальнейший рост интенсивности течения также длится достаточно долго: выход на стационарный режим происходит в момент времени около 450 с. При переменном коэффициенте термодиффузии усиление смесь разделения смеси осуществляется медленнее, чем при постоянном (Рис. 15б). Разделение смеси в стационарном режиме при этом уменьшается в 1,6 раза по сравнению со случаем постоянного коэффициента термодиффузии.

  

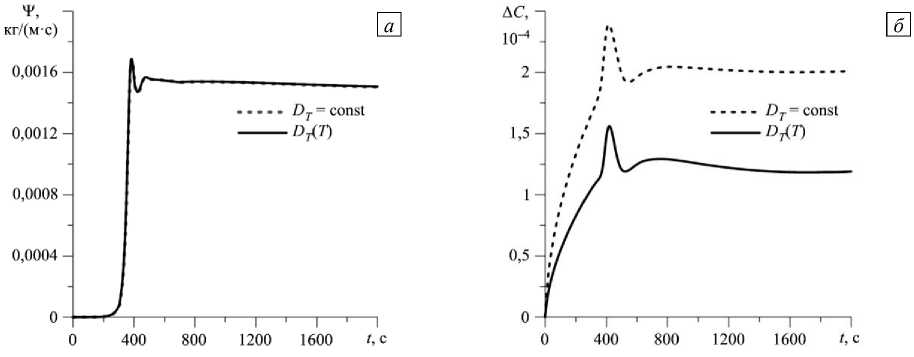
  Рис. 15. Временная эволюция максимального значения функции тока в полости (а) и разности концентраций между центрами верхней и нижней границ (б) при силе тяжести, в сто раз меньшей земной

  
  
  

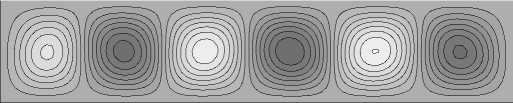
  Рис. 16. Изолинии функции тока при зависящем от температуры коэффициенте термодиффузии при силе тяжести, в сто раз меньшей земной, в момент времени t = 2000 с

  
  

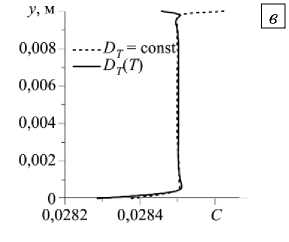
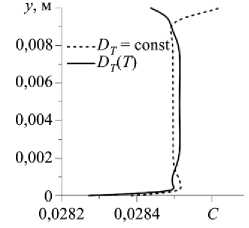
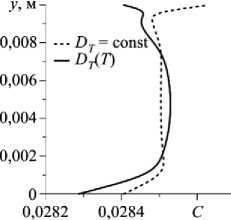
  Структура течения при t = 2000 с, что соответствует стационарному режиму, представлена на рисунке 16. Видно, что течение имеет 6-вихревую форму. Изолинии концентрации, как и при пониженной в 10 раз силе тяжести, «вморожены» в поле функции тока. При переменном коэффициенте термодиффузии изолинии концентрации отличаются от полученных при моделировании в случае постоянного коэффициента термодиффузии; из-за смены знака концентрация достигает максимального значения не у границы полости, а в ее центральной части (Рис. 17а, б), поэтому распределение смеси NaCl вдоль вертикальной центральной линии в средней части полости близко к начальному на рисунке 17а и заметно отличается от начального на на рисунке 17б . У горизонтальных границ концентрация резко меняется (Рис. 17в).

4.    Заключение

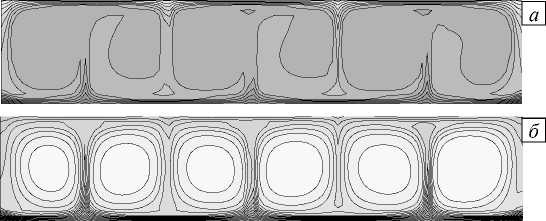
Рис. 17. Распределение концентрации примеси при постоянном ( а ) и зависящем от температуры ( б ) коэффициенте термодиффузии и профили концентрации ( в ) вдоль линии x = 0,005 м при силе тяжести, в сто раз меньшей земной, в момент времени t = 2000 с

в

Представлены результаты численного моделирования формирования и развития нелинейных режимов конвекции водного раствора поваренной соли в квадратной и прямоугольной, вытянутой в горизонтальном направлении, полостях. Расчеты выполнены с учетом зависимости коэффициента термодиффузии от температуры DT (T) по полиномиальному закону. Рассмотрен подогрев снизу; создаваемая при этом разность температур между горизонтальными границами равна 40 К. При такой разности температур у смеси внутри полости происходит смена знака коэффициента термодиффузии, что приводит к изменению направления градиента концентрации. Исследовано возникновение и развитие конвективных режимов в условиях земной и пониженной силы тяжести. В случае квадратной полости при земной силе тяжести формируется колебательное 4-вихревое течение с перезамыканием вихрей. При снижении силы тяжести течение становится стационарным 2-вихревым, а при еще меньшей гравитации — одновихревым. В прямоугольной полости при земной силе тяжести наблюдаются нерегулярные колебания значений характеристик течения. При снижении силы тяжести течение становится стационарным, его пространственный масштаб уменьшается.

Интенсивность течения достаточно высока, поэтому в центральной части полости поддерживается однородное распределение смеси. Возле границ имеют место большие градиенты концентрации примеси. Учет полиномиальной зависимости коэффициента термодиффузии от температуры слабо влияет на характер течения, однако смена знака коэффициента термодиффузии внутри полости приводит к значительному уменьшению, по сравнению с течением смеси при постоянном коэффициенте термодиффузии, максимальной степени разделения компонентов.

Работа выполнена при финансовой поддержке правительства Пермского края (Программа поддержки Научных школ Пермского края, Соглашение № С-26/788).