Влияние поперечного растяжения при обтяжке на пластические свойства материала деталей летательных аппаратов

Обтягивание сопровождается изгибом, значительным утонением и упрочнением материала заготовки. Возможности процесса значительно расширяются, если обтягивать предварительно изогнутые листовые заготовки.

В зависимости от схемы приложения внешних сил и формы обтягиваемой заготовки применяют простую с продольным растяжением обтяжку с большим технологическим припуском и поперечную с меньшим отходом материала и с влиянием на пластические свойства металла. Для обеспечения эксплуатационных свойств изготавливаемых деталей летательных аппаратов необходимо прогнозировать пластические свойства заготовки вначале технологического процесса изготовления обводообразующей детали. На первом этапе это возможно с применением математического аппарата.

Поперечное растяжение листовой заготовки в процессе обтяжки приводит к увеличению показателя жёсткости напряжённого состояния

П=⁽^ х ⁺^ у +^₂^)/^, -             (1)

где a i - интенсивность напряжений и влечёт за собой изменение предельной интенсивности истинной (логарифмической) деформации е , соответствующей моменту разрушения. Зависимость e ip = е ( П ) называется диаграммой пластичности. Она строится по экспериментальным данным, но для практических целей вполне подходит предложенная Г.А. Смирновым-Аляевым аппроксимирующая функция [1]:

£ ip =     '2 "^:7                  (2)

где – экспериментально определяемая вели- Барвинок Виталий Алексеевич, член-корреспондент РАН, доктор технических наук, профессор, заведующий кафедрой производства летательных аппаратов и управления качеством в машиностроении.

чина интенсивности истинной деформации образца, разрушаемого одноосным растяжением.

При одноосном растяжении отсутствуют поперечные напряжения, т.е. у_у= у_z= 0, а интенсивность напряжений

, (3)

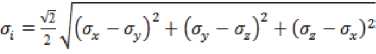
следовательно, показатель жёсткости напряженного состояния

П^э= ( у_х +0+0) /у_х ,=1.            (4)

Поперечные деформации при одноосном растяжении равны между собой и находятся из соотношения е = е=-м e x =- 0,5 e x , а интенсивность деформаций в этом случае равна

,(5)

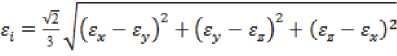
следовательно, можно считать, что

,(6)

где – истинная деформация разрушения образца в зоне шейки.

Используя (7) выразим деформацию через сужение:

ln. (8)

Из совместного решения (2), (6), (8) имеем

Экспериментально определяемые значения приводятся в справочной литературе. Так, для сплава Д16 величина сужения, согласно [2], составляет =0,25 (для Д16Т) и =0,55 (для Д16М).

Задача об оценке влияния поперечного растяжения на пластические свойства обтягиваемой листовой заготовки будет решена, если удастся установить зависимость

[ e x ]= f(а ),                 (10)

где [ e x ] - предельно допустимая деформация при обтяжке.

К числу критериев, используемых при назначении предельно допустимой деформации, могут относиться условие отсутствия разрушения, устойчивости нагружения, мелкозернистости структуры и др. В нашем случае будет использоваться критерий отсутствия разрушения.

При установлении зависимости (10) будем предполагать, что материал листовой заготовки является изотропным, т.е. его пластические свойства одинаковы в направлениях всех координатных осей: о хв = о ув = о в ; е хв = е ув = е в , где о в , е в - напряжение и деформация временного сопротивления.

Для удобства рассуждений в дальнейшем будем пользоваться безразмерными параметрами , изменяющимся в пределах 0<'^: --<1 и 7 . = J.. ,ко который может принимать как положительные, так и отрицательные значения.

При обтягиваемая листовая заготовка будет находиться в условиях одноосного растяжения. Такому состоянию, как было установлено выше, соответствует показатель жёсткости напряжённого состояния П =1 и интенсивность деформация

, (11) а безразмерный параметр будет равен

.

Итак, первая точка на диаграмме имеет координаты и =0.

Вторую точку на диаграмме ^Ех=^^а^ вы-берем из условия равенства нулю поперечной деформации .

Постоянство объёма при будет сохранено, если деформация е будет противоположной по знаку деформации c_v, т.е. e z =-c_v. При этом интенсивность деформации составит

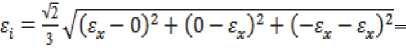
=       .                 (12)

Интенсивность напряжений функционально связана с интенсивностью деформаций экспериментально устанавливаемым при простом растяжении образца соотношением

.         (13)

Подставляя (12) и (13) в уравнении теории пластичности получим

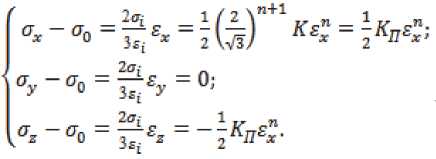
Напряжения при обтяжке обычно пренебрежимо малы по сравнению с и , поэтому считаем, что       . Тогда из третьего уравне ния системы (14) следует, что

Подставляя в первое и второе уравнения системы (14) получим        , тогда

<^ = КП^;

ау = ^^ = | а, У 2 "2

Интенсивность напряжений во второй точке будет равна

V7                                \ 2"V3

=      , (17)

а показатель жёсткости напряжённого состояния

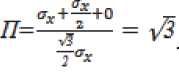
Из совместного решения (9), (12) и (18) для ,(19)

следовательно, безразмерный параметр во второй точке примет значение .

Поскольку напряжение составляет поло- вину от напряжения (второе уравнение (16)), безразмерный параметр во второй точке чис- ленно равен =0,5.

Таким образом, вторая точка на диаграмме имеет координаты 0,5 и

=0,5.

Теперь найдём координаты третьей точки на этой диаграмме. Будем считать, что она соответствует напряжению о^ ⁼ о в , т.е. безразмерному коэффициенту =1.

В этом случае деформация поперечного растяжения будет равна предельно допустимой деформации, вычисленной для первой точки

= , а деформация =-м -0,5. Из этого следует, что координаты третьей точки на диаграмме = численно имеют значения

г\. =-0,5?71=-0,5*1=-0,5 и ^..:=1.

Используя координаты этих трёх точек, диаграмму = можно аппроксимировать удобной для дальнейшего использования функцией вида

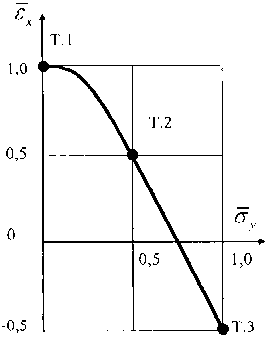
Рис. 1. Диаграмма зависимости безразмерного коэффициента , характеризующего величину предельной деформации обтяжки, от безразмерного коэффициента , характеризующего величину поперечного натяжения заготовки: т.1, т.2 и т.3 – характерные точки

+ b       ,        (20)

где a , b , c – коэффициенты, определяемые из условия прохождения аппроксимирующей функции через три заданные точки.

Подставив в (21) координаты трёх точек, получим систему линейных уравнений

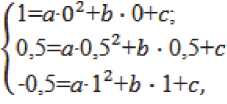
из решения которого следует, что a =-1, b =1/2, c =+1. При этом выражение (20) сводится к виду

+

Графическое изображение диаграммы = приведено на рис. 1.

Величина критических сжимающих напряжений находится в интервале от 1 до 5 кгс/ мм2, что соответствует безразмерному коэффи-

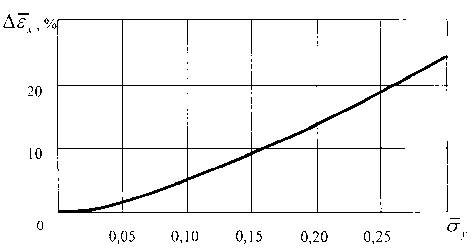
Рис. 2. Зависимость величины уменьшения предельно допустимой деформации обтяжки от степени поперечного натяжения

листовой заготовки циенту 0,05< ^- <0,25. Такого поперечного натяжения листовой заготовки (^..<0,25) будет вполне достаточно для исключения гофрообразова-ния при обтяжке. Дальнейшее увеличение никакой пользы не принесёт, а только уменьшит предельно допустимую величину деформации продольного растяжения.

На рис. 2 показан график зависимости величины уменьшения предельно допустимой деформации продольного растяжения листовой заготовки от величины её поперечного натяжения

+      •100% .(23)

На рис. 2 видно, что при =0,15…0,20 предельно допустимая деформация при обтяжке уменьшается на 10…15% от своего номинального значения, т.е. от того значения, которое соответствует обтяжке без поперечного натяжения листовой заготовки.