Влияние предварительного напряжения волокон на прочность полимерного композиционного материала

Для повышения конструкционных свойств композитов авторами было решено провести исследование предварительного напряжения упрочняющих волокон по аналогии с предварительно напряженным железобетоном. Сталь хорошо работает на растяжение, а бетон - плохо. Для предотвращения раннего растрескивания бетона от действия растягивающих напряжений производят предварительное растяжение стальной арматуры (после затвердевания, арматура находится в растянутом состоянии, а бетон в сжатом), это повышает несущую способность железобетона. Несмотря на очевидное усложнение технологии изготовления, выгода от повышения прочности на 30–100 % компенсирует затраты на производство.

У композитов волокна хорошо работают на растяжение, а смола - плохо, предел прочности и модуль упругости волокон в десятки раз больше, чем у смолы. Поэтому было решено провести теоретическое и экспериментальное исследование влияния предварительного напряжения волокон на прочность композита [1–7]. Сравнительный эксперимент напряженных и ненапряженных волокон композитов при испытании на растяжение должен показать насколько улучшаются механические свойства композитов при предварительном напряжении. Теоретическое исследование должно обосновать полученные преимущества, чтобы планировать количественные и качественные характеристики композитов и величину предварительного напряжения.

Материалы и методы исследования

Исследовались композиты, изготовленные на основе эпоксидной смолы, в качестве волокон использовалась стеклоткань или углеткань. Углеткань имеет более высокие механические характеристики (модуль упругости углеткани 150–400 ГПа, а модуль упругости стеклоткани 75–80 ГПа), примерно в таком же соотношении находятся и их пределы прочности.

Результаты исследования и их обсуждение

Расчет прочности на примере композита из стеклоткани с эпоксидной смолой.

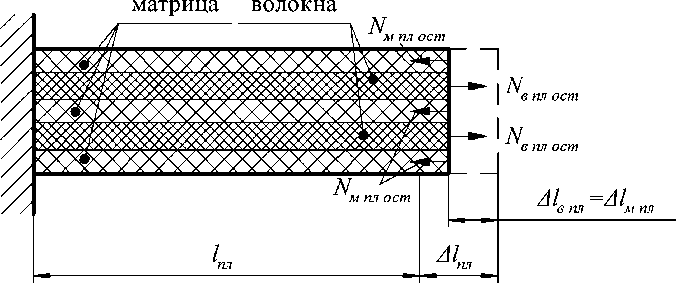
Рисунок 1 – Усилия, действующие в пластине после отверждения матрицы и снятия силы предварительного натяжения волокон F_пн :

N – остаточное усилие в волокнах пластины; N – остаточное усилие в пл ост                                               м пл ост в матрице пластины; lпл – начальная длина пластины; Δlпл – удлинение пластины под воздействием силы Fпн; Δlв пл = Δlм пл – укорочение соответственно волокон и матрицы пластины после снятия силы Fпн.

Определим нормальные силы, напряжения и деформации пластины из композита, возникающие при ее предварительном напряжении [8].

В ходе предварительного напряжения в волокнах стеклоткани возникло напряжение:

®в„ = ' п' = ^^J 2 = 1 , 98 - 10⁸ Па, ^Авпл 54 , 4 - 10 м

а соответствующее удлинение пластины составило:

F -I пн пл ^^пл   К А

^Ев A e пл

^ впл ^{- 1}пл 1 , 98 - 10 8 Па - 0 , 3 м

Е в

77 , 67 - 10 9 Па

= 7 , 66 - 10 - 4 м ,

где 1пл = 0, 3 м - начальная длина пластины; Ев = 77,67 -109 Па - модуль упругости волокон стеклоткани.

После затвердевания эпоксидной смолы и снятия силы предварительного натяжения F_пн произошло частичное укорочение волокон стеклоткани на величину:

А,..

F -N • / пн в пл ост пл

Е • А ввпл

где Nв пл ост – остаточное растягивающее усилие, действующее на волокна после снятия силы предварительного натяжения Fпн (рис. 1).

Матрица пластины после снятия силы F_пн укоротилась на величину:

м пл ост пл

^A мпл = ,—:----,                          ⁽⁴⁾

ммпл где N – остаточное сжимающее усилие в матрице пластины после снятия силы F м пл ост                                                                               пн

(рис. 1);

Е_м = 3 , 78 - 10⁹ Па - модуль упругости эпоксидной смолы.

Поскольку композитная конструкция представляет собой единое целое, то волокна и матрица пластины укоротились на одинаковую величину (А1впл = Alмпл), поэтому прирав- няем правые части выражений (3) и (4):

(р, -N

V пн ввплост ) ‘ пл _^N мпл ост ¹пл

Е ■ А               Е • А ввпл ммпл

Пластина после снятия силы Fпн и укорочения пришла в равновесное состояние, то есть сила растяжения волокон равна силе сжатия матрицы: Ne пл ост = Nм пл ост . С учетом этого, а также сокращая в (5) множитель lпл , получаем выражение:

пн м пл ост    м пл ост

.

ввпл    ммпл

Подставляя в (6) численные значения, приведенные выше, получим выражение:

¹⁰⁷⁸⁷ Н ^— N мпл ост    _       ^Nмпл ост

77, 67-109 Па - 54,4-10-6 м2 3, 78-109 Па - 25, 6-10-6 м2 , откуда получется значение остаточного сжимающего усилия в матрице пластины, по модулю равному остаточному растягивающему усилию в волокнах пластины:

N =N =241 52 Н м пл ост в пл ост ,.

Остаточное сжимающее напряжение матрицы пластины составило:

N м пл ост

^мпл ост =  j

Aмпл

241,52 Н = 9, 43 -106

25 , 6 - 10 ^{- 6} м²

Па ,

а остаточное растягивающее напряжение в волокнах пластины составило:

^Nв пл ост     241 , 52 Н            6

^ вплост     А впл     54 , 4 - 10 — ⁶ м² 4 , ^{44 10} .

Соотношение усилий, возникающих в волокнах и матрице композита при его растяжении, определяется выражением (4). Применяя его к изготовленным образцам и подставляя чис- ленные значения, имеем:

N Л вобр

N л мобр

E e "  ^Авобр _ 77 , 67 - 10⁹ Па - 8 , 16 - 10

К ■ A м мобр

।—6 »д2 м

3 , 78 - 10⁹ Па - 3 , 84 - 10 — ⁶ м²

= 43 , 66.

Таким образом, N _во бр = 43 , 66 - N _м обр , растягивающее усилие в волокнах образца, превышало таковое в матрице образца в 43,66 раза.

Определим напряжения, возникавшие в матрице и волокнах композитных образцов при их испытании на растяжение. Сначала рассмотрим образцы без предварительного напряжения наполнителя. Из условия равновесия следует, что внешняя нагрузка на образец равна сумме усилий, возникающих в волокнах и матрице образца. С учетом соотношения (9) запишем условие равновесия при растрескивании матрицы образца в виде:

^Fтрещ нн Ne обр нн трещ + Nм обр нн трещ

= 43 66 • N _Л + N _Л = 44 66 • N «

-га, w 1 v м обр нн трещ + 1 'мобрннтрещ ^>'”' 14 м обр нн трещ, где Nв обр нн трещ – усилие в волокнах непреднапряженного образца при растрескивании его матрицы;

N _{м обр нн трещ} – усилие в матрице непреднапряженного образца при ее растрескивании.

Из (10) определим усилие N _{м обр нн трещ} :

N          = ^Fтрещ нн 1027 Н

= 23 Н.

^{N мо}бр^нн трещ = 44, ₆₆ = 44, ₆₆

Тогда соответствующее напряжение в матрице ° _м обр _{нн трещ} составляет:

° мобр нн трещ

^Nм обр нн трещ       23 Н

А мобр

3 , 84 - 10 — ⁶ м 2

= 6 - 10⁶ Па.

Поскольку, как было определено ранее, усилие в волокнах превышало усилие в матрице в 43,66 раза, то:

^Nвобрннтрещ ⁴³ , ⁶⁶ " N м обр нн трещ ⁴³ , ⁶⁶ " ^{23 Н} 1004 Н .

Тогда напряжение в волокнах непреднапряженного образца при растрескивании матрицы составляло:

° вобр нн трещ

^Nв обр нн трещ      1004 Н

А вобр

8 , 16 - 10 — ⁶ м²

= 123 - 10 6 Па .

После развития трещин матрица потеряла свою несущую способность, поэтому будем считать, что при дальнейшем растяжении образца нагрузка воспринималась только волокнами. Тогда из условия равновесия разрушающая нагрузка непреднапряженного образца F _{разр нн} по модулю равна усилию в волокнах при разрушении N _{в обр нн разр} , и среднее напряжение в волокнах при разрушении ° _во бр _нн р _а3 р составляло:

° в обр нн разр

^Nв обр нн разр   ^Fразр нн      2194 Н

А вобр

А вобр    8 , 16 - 10 ^ м²

= 269 - 10 6 Па.

Это напряжение гораздо меньше предела прочности стеклоткани, так как при развитии трещин происходит многократная концентрация напряжений. Далее определим напряжения, возникавшие в матрице и волокнах преднапряженных образцов в ходе их испытания на растяжение. Согласно (7), остаточное сжимающее напряжение в матрице образцов после предварительного натяжения волокон составило 9, 43 -106 Па . При испытании на растяжение сжимаю- щее усилие в матрице постепенно уменьшалось, пока полностью не скомпенсировалось растягивающим усилием. В момент компенсации растягивающее усилие, действующее на матрицу, составило:

N комп м = ^ м пл ост - А м обр = 9 4 3 - 10 6 Па - 3 . 84 - 10 ^{- 6} м 2 = 36 . 23 Н.         (16)

Согласно (9), растягивающее усилие в волокнах образца в этот же момент было в 43,66 раза больше, чем в матрице:

Н комп в = 43 . 66 - N комп м = 43 . 66 - 36 . 23 Н = 1581 . 69 Н .                (17)

Из условия равновесия образца следует, что приложенная к нему растягивающая нагрузка равна сумме растягивающих усилий в волокнах и матрице; таким образом, в момент, когда сжимающее усилие в матрице от преднапряжения наполнителя полностью скомпенсировалось растягивающим усилием от растяжения, внешняя нагрузка составила:

Р комп = N компв + N компм = 1581 . 69 Н + 36 . 23 Н = 1617 . 92 Н . (18)

При данном значении внешней нагрузки напряжение в матрице образца равнялось нулю. Напряжение в волокнах составляет сумму напряжений от:

• 1)    остаточного растягивающего усилия, возникшего в волокнах после преднапряжения пластины (это напряжение, как следует из (8), равнялось 4,44∙10⁶ Па);

• 2)    растягивающей нагрузки, приложенной к образцу во время испытания. Суммарное

напряжение в волокнах в момент, когда напряжение в матрице становилось равным нулю, составляло:

+ Ркомп    44-1Q6Па+ 1617’92Н =203-106 Па uкомпв ивплост + А       ^’1V 11а + А 1V 11а .        (19)

А вобр                  8 . 16 -10 — ⁶ м²

При дальнейшем приложении нагрузки к образцу в его матрице возникало растягива- ющее напряжение, которое постепенно возрастало вплоть до момента растрескивания матрицы. Как следует из таблицы 2, трещины в матрице преднапряженных образцов начинали образовываться в среднем при нагрузке Гтрещ пн = 1490 Н . Усилия и напряжения в матрице и волокнах определим по аналогии с выражениями (10)–(15). По аналогии с (10)

F =N л     +^ к

1 трещ пн 1 в обр пн трещ +1 v м обр пн трещ

= 43 66 • N _л + N _л = 44 66 • N «

-га, ии 1ч м обр пн трещ +1 мо обр пн трещ ^’1' м обр пн трещ ’ где Nвобр пн трещ — усилие в волокнах преднапряженного образца при растрескивании его матрицы; Nм обр пн трещ — усилие в матрице преднапряженного образца при ее растрескива-

нии.

Из формулы (20) определим усилие N м обр пн трещ : Р трещпн_ = 14 90 Н N мобрпнтрещ    44 66 44 66 33 ’ 36 Н.                  ( ) Тогда соответствующее напряжение в матрице ^ м обр пн трещ составляет: _            Nмобрпнтрещ    33 . 36 Н    о m n ^ мобрпнтрещ =     ,          =,O/iia-6 2 = 8 ’ 69 , 10 Па.           (22) Амобр        3 ’ 84 " 10 м

Поскольку, как было определено в (9), усилие в волокнах превышало усилие в матрице в 43,66 раз, то:

N e обр пн трещ = 43 . 66 - N м обр пн трещ = 43 . 66 - 33 . 36 Н = 1456 . 5 Н .          (23)

Тогда среднее напряжение в волокнах преднапряженного образца при растрескивании матрицы составляло:

в обр пн трещ

° вобр пн трещ ^_

Aв обр

¹⁴⁵⁶ , 5 Н _ 178 __w 6 8 , 16 - 10 - ⁶ м 2

Па .

После развития трещин в матрице она потеряла свою несущую способность, поэтому будем считать, что при дальнейшем растяжении образца нагрузка воспринималась только волокнами. Тогда из условия равновесия разрушающая нагрузка преднапряженного образца Fразр пн по модулю равна усилию в волокнах при разрушении Nв обр пн разр , и напряжение в волокнах при разрушении овобр пн разр составляло:

в обр пн разр

° в обр пн разр ^_ j ^Ав обр

^Fразр пн _    ²⁴⁶⁵ Н    _ 302 _е iq6

А вобр    8 , 16 - 10 - ⁶ м²

Па .

Далее были определены механические характеристики изготовленных образцов в соответствии с [8] по следующим расчетным формулам:

• -    предел прочности при растяжении о В , МПа, определяется по формуле:

_     ^Fразр [ Н ]

^Ьобр ^{[ мм ]} "  h-обр ^{[ мм ]}

где Ь обр _ 15 мм - ширина образцов; Ь обр _ 0 , 8 мм - толщина образцов;

• -    прочность монослоя о ВМ , МПа, определяем по формуле:

М ° В [ МПа ]

° В _, n где n _ 2 - число слоев ткани в образцах;

• -    относительное удлинение при разрушении б , %, определяем по формуле:

Да_оа [ мм ]

б _ ^разР^ J . 100, а [ мм ]

где Дара3р - абсолютное удлинение рабочей зоны образцов при их разрушении; a _ 140 мм - начальная длина рабочей зоны образцов;

– модуль упругости при растяжении E , ГПа, определяется по формуле:

E _

До [МПа]

Де [ мм/мм ] • 1000 ’

где До - произвольно выбранное приращение напряжения на упругом участке нагружения;

^ДаЛо [ мм ]

Де _---_г - приращение деформации образцов, соответствующее приращению напря- а [ мм ]

жения До ; Да Д° - удлинение рабочей зоны образцов, соответствующее приращению напряжения До ; а _ 140 мм - начальная длина рабочей зоны образцов.

Перечисленные характеристики были определены для каждого из испытанных образцов, исключая бракованные образцы. Далее для каждой из перечисленных характеристик были определены (отдельно для серий испытаний преднапряженных и непреднапряженных образцов) следующие статистические величины:

– среднеарифметическое значение х по формуле:

n

_ Ё xi

x =                                            (30)

n где x – значение характеристики для каждого отдельного испытания; n – количество образ цов в серии (n = 4 для преднапряженных и непреднапряженных образцов);

• -    среднеквадратическое отклонение S n _— 1 по формуле:

  S n - 1 =

  
  

  ⁿ 2          ²

  Ё x i ^— n • ( x )

  i = 1

  n — 1

  
  
  
  

  – коэффициент вариации CV , % , по формуле:

CV = 100 • S n—L .

x

В таблице 1 представлены полученные значения предела прочности при растяжении и прочности монослоя изготовленных образцов, а также соответствующие статистические величины.

Таблица 1

Предел прочности при растяжении и прочность монослоя изготовленных образцов

Образцы с предварительным напряжением наполнителя			Образцы без предварительного напряжения наполнителя
№ образца	о Впн , МПа	о ВМпн , МПа	№ образца	о н», МПа Внн	оМ„ „, МПа Внн
1	169	85	1 (брак)	–	–
2	211	106	2	198	99
3	250	125	3 (брак)	–	–
4 (брак)	–	–	4	177	88
5	191	95	5	181	90
–	–	–	6	176	88
Статистические величины соответствующих характеристик
обозначение	преднапряженные образцы		непреднапряженные образцы
x	205	103	–	183	91
S n — 1	35	17		10	5
CV	17 %	17 %		6 %	6 %

Среднеарифметические значения предела прочности и прочности монослоя преднапря-женных образцов превышают таковые у непреднапряженных образцов на 12 %. То же можно сказать и о напряжениях, возникших в волокнах образцов при их разрушении (формулы (19) и (15)):

М

^ Впн  205 МПа   ^ Впн  103 МПа   ^ вобрпнразр  302 МПа

=          =       =          =               =           = 1,12.

о„„  183 МПа   М!   91 МПа   Ообпнн _пат  269 МПа

Внн               о d                 воир нн разр

Внн

Поскольку коэффициент вариации предела прочности и прочности монослоя у пред-напряженных образцов составил 17 % е [ 10 %; 20 % ] , то степень рассеивания данных - средняя. У непреднапряженных образцов коэффициент вариации составил 6% , что меньше 10 %, что свидетельствует о слабой степени рассеивания данных.

В таблице 2 представлены полученные значения абсолютного и относительного удлинения рабочих зон изготовленных образцов при их разрушении, а также соответствующие статистические величины для относительного удлинения.

Среднее арифметическое значение относительного удлинения при разрушении пред-напряженных образцов превышает таковое у непреднапряженных образцов на 1,6 %. Коэффициенты вариации относительного удлинения при разрушении как преднапряженных, так и не-преднапряженных образцов лежат в диапазоне [10 - 20 %], что позволяет говорить о средней степени рассеивания данных.

Таблица 2

Абсолютное и относительное удлинения рабочих зон изготовленных образцов при их разрушении

Образцы с предварительным напряжением наполнителя			Образцы без предварительного напряжения наполнителя
№ образца	Д аразр , мм	5, %	№ образца	Д аразр , мм	5, %
1	3,31	2,36	1 (брак)	–	–
2	4,86	3,47	2	4,87	3,48
3	4,94	3,53	3 (брак)	–	–
4 (брак)	–	–	4	4,21	3,01
5	3,83	2,74	5	4,32	3,09
–	–	–	6	3,3	2,36
Статистические величины
обозначение	преднапряженные образцы		непреднапряженные образцы
x	—	3,03	—	—	2,98
S n - 1		0,57			0,46
CV		18,83 %			15,6 %

В таблице 3 представлены полученные значения модуля упругости при растяжении изготовленных образцов, соответствующие приращения деформации образцов и удлинения их рабочей зоны, а также статистические величины, определенные для модулей упругости. Приращение напряжения на упругом участке нагружения До было выбрано равным 10 , 42 МПа .

Модуль упругости при растяжении изготовленных образцов

Таблица 3

Образцы с предварительным напряжением наполнителя				Образцы без предварительного напряжения наполнителя
№ образца	Д а д о , мм	Де , мм/мм	E, ГПа	№ образца	Д а д о , мм	Де , мм/мм	E, ГПа
1	0,14	1 ⋅ 10 -3	10,42	1 (брак)	–	–	–
2	0,13	9 , 3 - 10 - 4	11,22	2	0,16	1 , 14 - 10 - 3	9,11
3	0,15	1 , 07 - 10 - 3	9,72	3 (брак)	–	–	–
4 (брак)	–	–	–	4	0,16	1 , 14 - 10 - 3	9,11
5	0,14	1 ⋅ 10 -3	10,42	5	0,14	1 ⋅ 10 -3	10,42
–	–	–	–	6	0,13	9 , 28 - 10 - 4	11,22
Статистические величины
обозначение	преднапряженные образцы			непреднапряженные образцы
x	–	–	10,44	–	–	–	9,97
S n - 1			0,61				1,04
CV			5,85 %				10,4 %

Среднее арифметическое значение модуля упругости преднапряженных образцов превышает таковое у непреднапряженных образцов на 4,7 %. Коэффициент вариации модуля упругости преднапряженных образцов составляет менее 10 %, что свидетельствует о слабой степени рассеивания данных. У непреднапряженных образцов данный коэффициент лежит в диапазоне [10 - 20 %], соответственно, имеет место средняя степень рассеивания данных.

Что касается возникновения трещин в матрице растягиваемых образцов, то соответствующие напряжения в матрице и волокнах преднапряженных образцов на 45 % превышали таковые в непреднапряженных образцах. Это можно увидеть из сравнения значений, полученных по формулам (14) и (17), а также по формулам (14) и (18) соответственно:

178 - 10⁶ Па _Л ---------7-----= 1 , 45.

123 - 10⁶ Па

° м обр пн трещ _ 8 , 69 " 10^ Па _ ^о в обр пн трещ ^о м обр нн трещ    6 • 10^ Па ^ в обр нн трещ

Таким образом, образцы, наполнитель которых подвергался предварительному напряжению, при испытании на растяжение дольше сохраняли свою целостность.

Для построения диаграммы деформирования в координатах «деформация е, % -напряжение о, МПа » был определен вектор значений внешней нагрузки при испытании об- разцов на растяжение:

Diag F = ( 0 , 60 , 125 , 150 , 175 , 250 , 375 , 500 , 750 , 1000 , , 3000 ) Н . (35)

'V'

18 элементов

Максимальное значение в векторе ( 3000 Н ) соответствует максимальной разрушающей нагрузке, зафиксированной в ходе испытаний (образец № 3 с предварительным напряжением наполнителя). Путем деления элементов данного вектора на площадь поперечного сечения образцов А обр = 12 мм получен соответствующий вектор значений напряжений при испытании образцов на растяжение:

Diag _G = ( 0 , 5 , 10 , 42 , 12 , 5 , ..., 250 ) МПа .                     (36)

'-----------------------------------------------V-----------------------------------------------'

18 элементов

Для каждой из нагрузок, перечисленных в векторе Diag _F , и для каждого изготовленного образца (за исключением бракованных образцов) в ходе испытаний на растяжение фиксировалось соответствующее удлинение рабочей зоны образца. Затем подсчитывалось среднее арифметическое значение по всем испытанным образцам для каждой из нагрузок, перечисленных в векторе Diag _F . В результате были получены два вектора, один из которых содержит средние арифметические значения удлинений рабочих зон преднапряженных образцов, а второй – непреднапряженных образцов:

DiagAa avg_пн = (0, 0,15, 0,42, 0,57, ..., 4,8) мм; '------------------------------------------V

18 элементов

___________________.(37)

Diag A a avg_нн = ( 0 , 0 , 04 , 0 , 2 , 0 , 38 , ..., 3 , 76 ) мм.

'------------------------------------------V'

15 элементов

В векторе DiagAa avg нн содержится меньше элементов, чем в векторе DiagAa avg пн , так как максимальные удлинения рабочей зоны непреднапряженных образцов перед их разрушением в среднем были меньше, чем у преднапряженных. Путем деления элементов данных векторов на начальную длину рабочей зоны образцов a = 140 мм получены соответствующие векторы деформаций для преднапряженных и непреднапряженных образ- цов:

Diag _{e пн} = ( 0 0 , 0011 , 0 , 003 , 0 , 0041 , ..., 0 , 0343 ) ; Ч______________________________________________________V______________________________________________________V

18 элементов

Diag _e нн = ( 0 0 , 0003 , 0 , 0014 , 0 , 0027 , ..., 0 , 0269 ) .

Ч .                                                                         V

15 элементов

Далее для построения диаграмм деформирования проведено линейное интерполирование соответствующих векторов. Как следует из (38), диапазон значений деформаций Diag Ag = max ( Diag _g ) - min ( Diag _e ) составил 0 , 0343 для преднапряженных образцов и

0,0269 для непреднапряженных. При шаге интерполирования, равном 1 100 диапазона значе- ний деформаций, векторы интерполяционных точек имеют вид:

e step пн = ( 0 , 0 , 00034 , 0 , 00068 , ..., 0 , 0343 ) ;

101 элемент gtpn „„=(0, 0,00027, 0,00054, ..., 0,0269). step _ нн

ЧV"

101 элемент

Применив в интерполяционных точках процедуру линейного интерполирования с использованием векторов (37) и (38) при помощи встроенной функции «linterp» системы компьютерной алгебры «Mathcad», получили диаграммы деформирования преднапряженных и не-преднапряженных образцов, представленные на рисунке 2.

Напряжение ст, МПа

i 4 4 рТочка перехода i f 4-•i f | " (преднапряженные образцы) J Точка перехода] 1 1 i 1 12 / (непреднапряженные образцы).! 1 L пер_пн :        :        :        :        :        : 1 i /

. пернн

участок 1

участок 2

р перни

р перпн

участок 3

0 0,2 0,4 0,6 0,8 1 1,2 1,4 1,6 1,8 2 2,2 2,4 2,6

2,8 3 3,2 3,4 3,6 Деформация с, %

—*— Преднапряженные образцы

-— Непреднапряженные образцы

Рисунок 2 – Диаграммы деформирования испытанных образцов:

е пер пн ^{и а} пер пн — деформация и напряжение перехода преднапряженных образцов;

е пер нн и ^а пер нн — деформация и напряжение перехода непреднапряженных образцов;

• 1    – точка, соответствующая напряжению перехода преднапряженных образцов;

• 2    – точка, соответствующая напряжению перехода непреднапряженных образцов

Значения деформаций по горизонтальной оси выражены в процентах путем умножения значений элементов векторов (38) и (39) на 100. На диаграммах выражен начальный участок текучести (участок 1 на рис. 2), которая продолжается до достижения деформации 0,6 % у преднапряженных образцов и 0 , 4 % у непреднапряженных, напряжения при этом не превышают 12 Мпа. Далее начинается упругий участок диаграмм (участок 2 на рис. 2), на котором деформации растут пропорционально напряжениям; с ростом напряжений соответствующий рост деформаций несколько ускоряется (участок 3 на рис. 2), угол наклона диаграмм к оси деформаций постепенно уменьшается вплоть до разрушения образцов. Условные точки перехода между вторым и третьим участками диаграмм определяются графически. Для этого проводятся линии, касательные к соответствующим участкам. Указанные точки находятся на пересечении этих линий. Для каждой точки определяются соответствующие деформация ( е _пер пн , е _пер нн ) и напряжение ( ст _{пер пн} , ст пер _нн ) перехода. Для определения деформаций перехода опускаются перпендикуляры из точек перехода на ось деформаций. Получены следующие значения: деформация перехода преднапряженных образцов е пер _пн = 1 , 97 % , непреднапряженных образцов е пер _нн = 1 , 73 % ; деформация перехода преднапряженных образцов больше на 13 , 9 % . Далее для определения напряжений перехода из точек пересечения указанных перпендикуляров с соответствующими диаграммами (точки 1 и 2 на рис. 2) опускаются перпендикуляры на ось напряжений. Получены следующие значения: ст пер пн = 146 , 55 МПа, ст пер _нн = 126 , 1 МПа; напряжение перехода преднапряженных образцов больше на 16 , 2 % . Таким образом, переход от второго к третьему участку диаграммы деформирования у преднапряженных образцов происходит при больших напряжениях и деформациях, чем у непреднапряженных, что свидетельствует о большем запасе прочности пред-напряженных образцов.

Заключение

Если волокна композита натянуть, то после затвердевания матрицы волокна испытывают растягивающие напряжения и более равномерно воспринимают приложенную нагрузку, а матрица испытывает сжимающие напряжения, и трещины в ней возникают при большей нагрузке.

Отсутствие перегрузки волокон привело к увеличению предела прочности преднапря-женных образцов по сравнению с непреднапряженными, также выросли относительное удлинение и модуль упругости. Предварительное напряжение волокон композита привело к возникновению остаточных сжимающих напряжений в его матрице, что увеличило пределы прочности и модуль упругости композита.

Сравним результаты испытания на растяжение образцов композита из стеклоткани и углеткани.

Таблица 4 Сравнение результатов испытания на растяжение образцов композита из стеклоткани и углеткани (приведены средние арифметические значения)

Тип образцов	Растягивающая сила трещинообразования Р т ре щ , Н		Максимальная (разрушающая) сила F   Н разр ,
	стеклоткань	углеткань	стеклоткань	углеткань
Преднапряженные	1490	2682	2465	3435
Непреднапряженные	1027	1226	2194	2619

Сила трещинообразования преднапряженных образцов из стеклоткани на 45 % , а из углеткани – на 119 % больше, чем у непреднапряженных образцов.

Сила разрушения преднапряженных образцов из стеклоткани на 12 % , а из углеткани на 31 % больше, чем непреднапряженных. В то же время модуль упругости стеклоткани составляет 77 , 67 ГПа (см. табл. 1), а модуль упругости углеткани – 240 ГПа . Отсюда следует вывод: чем выше исходные механические характеристики наполнителя, тем больший эффект приносит его предварительное напряжение.

Таким образом, можно сделать вывод, что предварительное напряжение наполнителя повышает прочностные свойства композиционных материалов и может быть рекомендовано к внедрению в производство композитных конструкций, что подтверждают результаты других исследований [9 - 15].

Предметом дальнейших исследований будут служить определение оптимальной силы предварительного натяжения наполнителя F_пн и разработка технологии изготовления сложных конструкций из композиционных материалов с предварительным натяжением их наполнителя.

Работа выполнена в рамках программы «Приоритет-2030» ФГБОУ ВО ИРНИТУ «i.DIT».